Flux et spectre
Auteurs: Emmanuel Marcq, Loic Rossi
- Décrire
- Les composantes du flux
- Flux stellaire
- Corps telluriques
- Les planètes géantes
- Le flux thermique
- Analyse de composition atmosphérique
- Analyse du profil thermique
- Méthodes
- Observations nadir et limbe
- Transits et occultations
- Comprendre
- Transfert radiatif
- Processus radiatifs
- Épaisseur optique / Loi de Beer-Lambert
- Diffusions Rayleigh et Mie
- Surfaces
- Température de brillance
- Méthodes
- Nadir
- Sondages thermiques
- Sondages de composition
- Spectre réfléchis
- Occultations et transits
- Occultations
- Transits primaires
- Transits secondaires
- Se Tester
- QCM de cours
- Transit primaire
- Sondage thermique
- Mini-projet
- Occultation stellaire à travers l'atmosphère de Vénus
- Simulation d'une occultation stellaire à travers l'atmosphère de Vénus
-
Rayonnement électromagnétique : Flux et spectre
 Objectifs
Objectifs
Ce chapitre a pour but de présenter ce que peut nous apprendre l'observation du flux émis ou réfléchi par l'atmosphère ou la surface d'une planète (ou d'une exoplanète).
 Prérequis
Prérequis
Pour ce chapitre il est préférable d'avoir une connaissance préalable des concepts suivants :
- de spectre électromagnétique : infrarouge (IR), visible, ultraviolet (UV) notamment ;
- des différents processus radiatifs : rayonnement de corps noir, diffusion, absorption, réflexion ;
- et enfin de la structure verticale d'une atmosphère planétaire.
Décrire
Auteurs: Loïc Rossi, Emmanuel Marcq
Les composantes du flux
Le flux radiatif reçu de la part d'une planète peut être analysé comme la somme de deux composantes :
- le flux thermique de la planète, lié à son émission propre (dépendant notamment de sa température)
- le flux réfléchi, émis par son étoile puis diffusé par l'atmosphère et/ou la surface de la planète
Séparation des composantes
Ces deux composantes seront traitées séparément dans la suite de ce chapitre. En général, les planètes sont largement plus froides que la photosphère de leur étoile, si bien que le flux réfléchi et le flux thermique s'observent de façon disjointe dans le spectre de la planète (voir figure). Cependant, ce n'est pas le cas pour les exoplanètes très chaudes, pour lesquelles le recouvrement des deux composantes n'est pas négligeable si bien que la séparation entre ces deux catégories perd de sa pertinence.
Composantes réfléchie et thermique
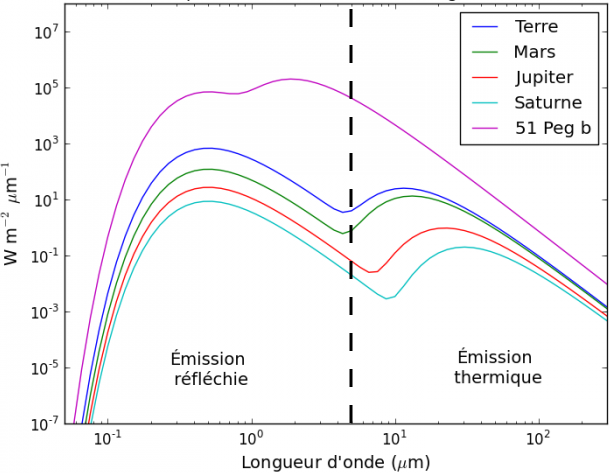
Irradiances spectrales émises ou réfléchies en provenance de quelques atmosphères planétaires. On distingue les deux composantes : la composante thermique du corps et la composante correspondant au flux solaire ou stellaire réfléchi par la planète. Cette distinction perd de son sens physique pour une planète très chaude comme 51PegB.
Crédit :
Loïc Rossi CC-BY-SA
Dans le cas du système solaire, il est usuel de traiter le flux à des longueurs d'onde plus courtes que 5 µm (incluant donc l'UV, le visible et l'IR proche) comme provenant quasi-exclusivement du Soleil, et les longueurs d'onde plus grandes comme provenant de l'émission thermique du corps observé (incluant donc l'IR moyen et lointain, ainsi les domaines sub-millimétrique et radio). La relation mathématique entre température d'un corps noir et la longueur d'onde du maximum spectral s'appelle la loi de Wien : pour une étoile de température de surface voisine de quelques milliers de Kelvins, il se situe dans le domaine visible voire UV, tandis que pour une planète de température effective voisine de quelques dizaines à quelques centaines de Kelvins, il se situe dans le domaine IR.
Flux stellaire
Corps telluriques
Les planètes du système solaire constituent un cas particulier intéressant puisque l'on peut résoudre leur disque et même effectuer des observations en orbite. Il est même possible pour les planètes telluriques de distinguer le flux diffusé au sein de l'atmosphère de celui réfléchi ou diffusé par leur surface solide (voire liquide dans le cas de la Terre et de Titan).
Observations atmosphériques
Dans le cas de Mars et Vénus, les spectres dans l'infrarouge proche de ces planètes sont dominés par l'absorption due au dioxyde de carbone (CO2), composant majoritaire de leurs atmosphères. Dans l'ultraviolet, le spectre de Vénus est dominé par l'absorption due au dioxyde de soufre (SO2) ainsi que par un absorbant dont la composition n'est pas encore connue. Dans le cas de la Terre, ce même domaine spectral est dominé par l'absorption due à la vapeur d'eau et au CO2 (ainsi qu'au méthane dans une moindre mesure), tandis que le spectre visible et UV révèle la présence d'ozone O3 et de dioxygène O2. Le spectre réfléchi de Titan est quant à lui largement dominé par l'absorption du méthane CH4 et des aérosols présents dans son atmosphère.
Spectre de la Terre vu par Galileo
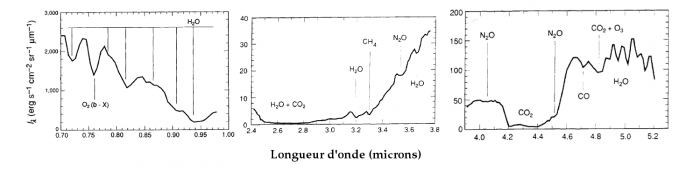
Luminance spectrale en provenance de la Terre et observée par la sonde Galileo alors en route vers Jupiter. Les spectres révèlent de grandes quantités d'eau, d'oxygène ainsi que du méthane. Les quantiés mesurées par Galileo témoignent d'une activité biologique intense.
Crédit :
Adapté de Sagan et al. (1993).
La nature physique des objets diffuseurs varient selon le corps observé. Au sein de l'atmosphère terrestre, la diffusion est principalement le fait des molécules d'air (régime de Rayleigh), ainsi que des nuages d'eau (recouvrant à tout moment environ 50% de notre planète). Pour Vénus, les nuages épais et omniprésents empêchent toute observation de la surface en lumière solaire. Dans le cas de Mars, l'atmosphère peu dense ne crée pas beaucoup de diffusion Rayleigh, en revanche les poussières soulevées dans l'atmosphère par les tempêtes ainsi que les nuages de glace contribuent à la diffusion de la lumière solaire vers l'observateur de façon significative.
Nuages de Vénus en UV

Photographie en UV proche (365 nm) des nuages supérieurs de Vénus côté jour. La nature physique des contrastes observés est encore en partie mystérieuse à ce jour.
Crédit :
ESA (mission Venus Express)
Observations des surfaces
L'observations des surfaces de Mars et de la Terre depuis l'espace permettent de déterminer partiellement leurs compositions : la surface de Mars comporte ainsi des oxydes de fer en quantité significative qui lui donnent cette teinte "rouillée". La présence de silicates et de phyllosilicates (dont des argiles) est également décelable, ainsi que celle de sulfates.
Surface martienne

Panorama martien observé par le rover Curiosity de la NASA. La couleur caractéristique de la surface martienne apparaît clairement, ainsi que la diffusion de la lumière par les poussières en suspension dans l'atmosphère.
Crédit :
NASA
Sur Terre, en plus des silicates et autres roches nues visibles dans les déserts, la végétation (chlorophylle) présente une absorption caractéristique en infrarouge proche. De plus, les étendues liquides (mers, océans) sont nettement reprérables également, via le phénomène de réflexion spéculaire (miroitante) typique des surfaces lisses.
Chlorophylle vue en IR proche

Photographie en IR proche de la rivière Neckar en Allemagne. La réflectance très élevée de la chlorophylle des arbres est particulièrement frappante.
Crédit :
Cyrill Harnischmacher
Dans le cas de Titan, les observations de surface sont limitées à quelques fenêtres spectrales dans l'IR proche. Ces dernières révèlent des zones claires et sombes indiquant une présence variable de composés organiques sombres (par rapport à la glace environnante) à la surface. Le phénomène de réflexion spéculaire est également observé près des régions polaires, indiquant par là la présence de lacs d'hydrocarbures liquides.
Réflexion spéculaire sur les lacs de Titan

Réflexion en IR proche de la lumière solaire à la surface d'un lac de Titan situé près du pôle Nord.
Crédit :
NASA (mission Cassini)
Les planètes géantes
Dans le cas des planètes géantes, il n'y a pas de surface à observer, seule l'atmosphère contribue au flux réfléchi. Il est difficile de sonder très profondément dans ces atmosphères, l'opacité (par absorption et diffusion) au sein de ces atmosphères croissant rapidement avec la profondeur en dessous des nuages visibles (constitués de NH3 ou NH3SH pour Jupiter et Saturne, de CH4 pour Uranus et Neptune).
L'absorption de certaines longueurs d'onde dans le visible nous renseigne aussi sur la composition gazeuse et/ou particulaire. Uranus et Neptune apparaissent ainsi bleu-vert en lumière visible à cause de l'importante épaisseur travsersée de méthane gazeux qui absorbe davantage dans le rouge. À l'inverse, sur Jupiter et Saturne, les brumes photochimiques situées en altitude comportent des chromophores de composition encore inconnue et absorbant l'UV et le bleu, ce qui donne à ces planètes une teinte globalement jaune-orangée.
Spectres des planètes géantes dans le domaine visible
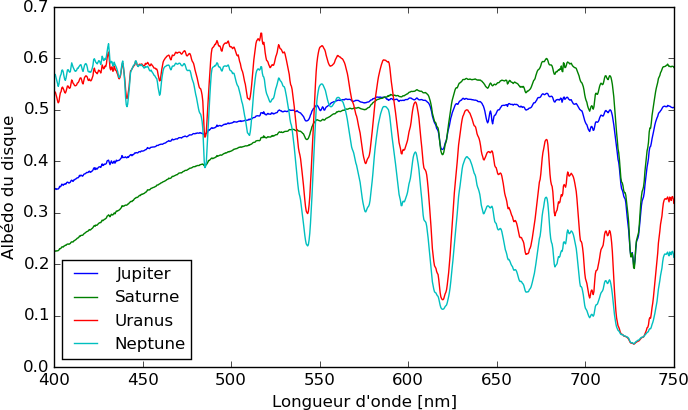
Spectres d'Uranus, Neptune, Saturne et Jupiter dans le domaine visible. On notera le faible
albédo de Jupiter et Saturne dans le bleu ainsi que les fortes absorptions d'Uranus et Neptune dans le rouge (liées au méthane).
Crédit :
Adapté de Karkoschka (1994).
Apparence visuelle des planètes géantes du système solaire
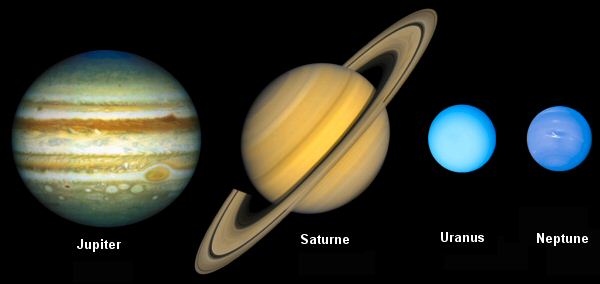
Le flux thermique
Auteurs: Loïc Rossi, Emmanuel Marcq
Analyse de composition atmosphérique
L'analyse du spectre thermique permet d'identifier divers composés (surtout atmosphériques) de par la présence de bandes ou de raies spectrales caractéristiques d'une espèce chimique.
Système solaire
Les spectres thermiques en provenance des planètes du système solaire nous renseignement notamment sur :
- Vénus & Mars Présence de CO2, de H2O, de CO, de nuages (et/ou de poussières dans le cas de Mars). Pour Vénus, le sondage thermique s'étend même sous les nuages dans quelques fenêtres de transparence laissées par CO2, permettant des mesures profondes de CO, OCS, de la vapeur d'eau H2O et son isotope lourd HDO, de SO2, HF, HCl, etc.
- Planètes géantes Présence de raies d'absorption de divers hydrocarbures légers CxHy, d'ammoniac NH3 et de phosphine PH3. Pour Jupiter et Saturne, le sondage thermique s'étend sous les nuages dans quelques fenêtres de transparence laissées par H2 et He, permettant ainsi des mesures profondes de H2O, CO, NH3, PH3, l'isotope lourd du méthane CH3D, et même à l'état de traces les hydrures métalliques GeH4 et AsH3.
- Titan Présence de CH4, de nitriles, d'hydrocarbures, d'un brouillard photochimique et de nuages de CH4 condensé.
Notons que ces mêmes techniques sont également utilisées depuis l'orbite terrestre pour des mesures satellitaires de composition atmosphérique, notamment pour des mesures météorologiques (nuages, vapeur d'eau) ou climatologiques (CO2).
Spectres thermiques telluriques
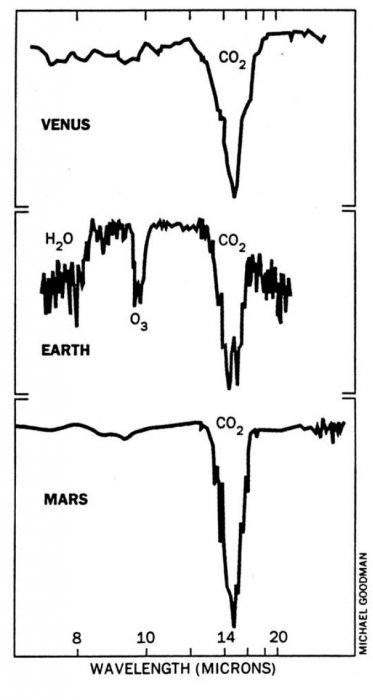
Spectres des trois principales planètes telluriques connues dans l'infrarouge thermique. Les composés gazeux responsables des structures observées sont indiqués.
Crédit :
NASA GSFC (Hanel et al.)
Images IR thermiques de la Terre

À gauche : image Météosat dans le canal 10,5-12,5 µm (fenêtre de transparence atmosphérique). À droite : image Météosat dans le canal 5,7-7,1 µm (zone d'opacité de H2O)
Exoplanètes
Les spectres thermiques d'exoplanètes que nous sommes en mesure d'observer sont évidemment de bien moins bonne qualité que pour les objets du système solaire. Ils ne sont pas résolus spatialement (aspect ponctuel des exoplanètes), et sont en général de résolution spectrale assez faible (car on ne peut se permettre de trop disperser spectralement un flux reçu qui est en général très faible). Nous disposons néanmoins à ce jour des connaissances suivantes :
Analyse du profil thermique
Lorsque la composition de l'atmosphère est connue, la forme exacte des raies spectrales vues dans le spectre thermique peut donner à l'observateur des renseignements sur la température du milieu responsable de l'émission thermique (que ce soit la surface ou l'atmosphère). Ainsi, une atmosphère où le profil thermique décroît avec l'altitude présentera des raies en absorption, tandis qu'une atmosphère où la température croît avec l'altitude (une stratosphère, donc) présentera des raies d'émission. Une explication plus détaillée est disponible ici.
L'utilisation de ces spectres pour la mesure du profil thermique n'est possible que dans une plage limitée d'altitude selon la raie observée. Elle nécessite également un gaz dont le profil vertical d'abondance est bien connu dans l'atmosphère : c'est le cas de CO2 sur Mars et la Terre par exemple. Il est hélas impossible de se livrer à la fois à des mesures de profils de composition et de température simultanément...
Spectre thermique de Mars
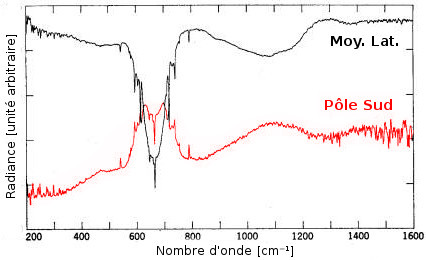
Spectres thermiques enregistrés par la sonde Mariner 9 en orbite autour de Mars. Le profil thermique est décroissant avec l'altitude dans les moyennes latitudes, mais croissant au pôle sud comme le montre la bande de CO2 tantôt en absorption ou en émission.
Crédit :
Tiré de Hanel et al. (1972)
Exoplanètes
L'observation indirecte (par différence avec le spectre stellaire pur observable lors d'un transit secondaire) du flux thermique émis par des exoplanètes géantes permet, moyennant des hypothèses raisonnables sur leur composition, d'estimer la température des couches atmosphériques émettrices. Cependant, la faiblesse du signal impose une résolution spectale très faible, hélas insuffisante pour dériver un véritable profil vertical de température.
Méthodes
Auteurs: Loïc Rossi, Emmanuel Marcq
Observations nadir et limbe
 Géométrie d'une observation planétaire
Géométrie d'une observation planétaire
Pour décrire la géométrie d'une observation planétaire, il faut au moins trois angles, que l'on choisit conventionnellement de la façon suivante :
- l'angle solaire zénithal
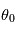 (SZA, pour Solar Zenith Angle) : c'est l'angle entre la direction du zénith et la direction du Soleil ;
(SZA, pour Solar Zenith Angle) : c'est l'angle entre la direction du zénith et la direction du Soleil ; - l'angle d'émission
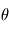 (EMI) : c'est l'angle entre la direction du zénith et celle du rayon émergent/diffusé ;
(EMI) : c'est l'angle entre la direction du zénith et celle du rayon émergent/diffusé ; - l'angle de phase
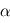 : c'est l'angle entre la direction du Soleil et la direction de l'observateur.
: c'est l'angle entre la direction du Soleil et la direction de l'observateur.
Géométrie d'une observation spatiale
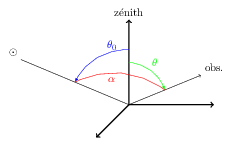
Géométrie d'observation : en bleu
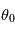
est l'angle solaire zénithal (SZA) ; en vert
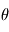
est l'angle d'émission (EMI) ; et en rouge l'angle
α est l'angle de phase.
Crédit :
Loïc Rossi CC-BY-SA
Observation nadir
L'observation en nadir consiste à observer la planète en pointant l'instrument vers son centre. On observe donc l'atmosphère ou la surface qui se trouve directement sous la sonde. Cela correspond à un angle d'émission nul. Cependant, cette condition n'est jamais rigoureusement respectée, et on considère qu'une observation est en nadir tant que l'on peut négliger la courbure planétaire, ce qui donne une limite pour l'angle d'émission de l'ordre de 30° pour des observations depuis l'orbite basse.
Observations au limbe
Pour les observations au limbe, on observe la planète selon une incidence rasante ; en d'autres termes l'angle d'émission est proche de 90°. Dans cette configuration la courbure planétaire n'est pas négligeable : on ne peut plus considérer l'atmosphère comme constituée de couches planes parallèles. Le principal avantage de l'observation au limbe est que la résolution spatiale se traduit directement en résolution verticale, tandis que les observations nadir sont en général peu précises selon cette direction (mais plus adaptées à une cartographie horizontale). Un autre avantage des observations au limbe est la démultiplication des épaisseurs optiques traversées par les rayons lumineux au sein des différentes couches, ce qui se traduit par des gains substantiels de sensibilité pour la détection et la mesure d'espèces à l'état de traces.
Observations au limbe et au nadir
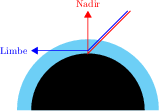
Géométries d'observations au limbe (bleu) et au nadir (rouge).
Crédit :
Emmanuel Marcq CC-BY-SA
Transits et occultations
 Transits primaires
Transits primaires
Un transit primaire désigne le phénomène d'éclipse partielle d'une étoile par une planète et son atmosphère. L'occultant présente alors un diamètre apparent petit devant l'occulté. Un exemple connu dans le système solaire est celui du transit de Vénus, mais l'étude de ce phénomène a connu un regain d'intérêt avec son application à la détection et à la caractérisation d'exoplanètes.
Si la planète dispose d'une atmosphère, une partie de la lumière stellaire va traverser cette atmosphère pendant le transit primaire. L'observation du spectre transmis permet alors de mesurer quelle extinction supplémentaire est causée par l'atmosphère de la planète à différentes longueurs d'onde, permettant ainsi de contraindre la nature physico-chimique de ses constituants.
 Transits secondaires
Transits secondaires
Un transit secondaire désigne le phénomène réciproque : c'est à présent l'étoile qui masque la planète, le plus souvent totalement étant donné que les étoiles sont bien plus grandes que les planètes.
Immédiatement avant et après un transit secondaire, on peut observer, en plus du spectre de l'étoile seule telle qu'elle apparaît en l'absence de transit, une contribution supplémentaire due au spectre émis ou réfléchi par la planète. Il est alors possible, par soustraction entre le spectre composite observé et celui de l'étoile seule (spectroscopie différentielle), d'analyser le spectre émis ou réfléchi par la planète seule. Une telle méthode exige toutefois une grande sensibilité, car la contribution d'origine planétaire est beaucoup moins intense que celle en provenance de l'étoile.
 Occultations
Occultations
Une occultation (solaire ou stellaire) désigne un phénomène physiquement analogue à un transit primaire (l'occulté est une étoile, l'occultant une planète), mais où cette fois l'occulté est de diamètre apparent très petit devant l'occultant. L'observabilité des occultations s'accroît avec la proximité de l'observateur à l'occultant (à sa surface ou en orbite basse). Un coucher de Soleil est un exemple d'occultation d'observation quotidienne aisée. Il est toutefois possible d'observer des occultations loin de l'occultant, notamment depuis la Terre, entre un corps du système solaire et une étoile lointaine. Un autre type d'occultation aussi utilisé consiste en l'utilisation comme source de l'émetteur radio d'une sonde spatiale. L'occultant est alors l'atmosphère autour de laquelle orbite la sonde, et l'observation se fait à partir de radiotélescopes sur Terre.
L'extinction progressive (à mesure que l'occultant se place devant l'occulté) du rayonnement en provenance de la source permet alors de déduire les propriétés optiques des différentes couches atmosphériques traversées.

Illustration des transits primaire (en haut à gauche), secondaire (en bas à gauche) et d'une occultation stellaire (à droite).
Crédit :
Gauche : CNES ; Droite : ESA
Comprendre
Auteurs: Loïc Rossi, Emmanuel Marcq
Transfert radiatif
Auteurs: Loïc Rossi, Emmanuel Marcq
Processus radiatifs
L'interaction entre le rayonnement (ondes du champ électromagnétique) et la matière (chargée au niveau microscopique : électrons, noyaux atomiques) se caractérise par trois types de processus radiatifs : l'absorption, l'émission et la diffusion.
Émission
Un processus d'émission intervient lorsque la matière cède localement de l'énergie au champ électromagnétique (création d'un photon). Cette émission est qualifiée de thermique lorsque le champ et la matière sont à l'équilibre thermodynamique à une même température 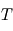 (on peut voir alors leur interaction comme celle d'un gaz de photons perpétuellement absorbés et émis par la matière environnante, et se mettant en équilibre de la sorte). Il existe également des phénomènes d'émission non thermiques (ex: fluorescence, émission laser), mais ils sortent du cadre de ce cours ; certains de ces processus sont vus dans ce chapitre.
(on peut voir alors leur interaction comme celle d'un gaz de photons perpétuellement absorbés et émis par la matière environnante, et se mettant en équilibre de la sorte). Il existe également des phénomènes d'émission non thermiques (ex: fluorescence, émission laser), mais ils sortent du cadre de ce cours ; certains de ces processus sont vus dans ce chapitre.
Illustration d'un processus d'émission spontanée
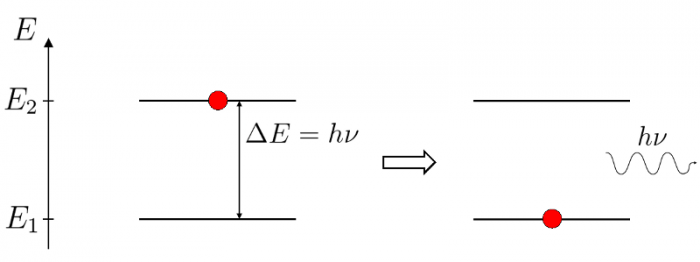
Émission spontanée d'un photon par un système matériel possédant au moins deux niveaux d'énergie. L'énergie totale est conservée dans ce processus.
Absorption
Un processus d'absorption a lieu lorsqu'inversement, le champ électromagnétique cède de l'énergie à la matière environnante (destruction d'un photon).
Illustration d'un processus d'absorption
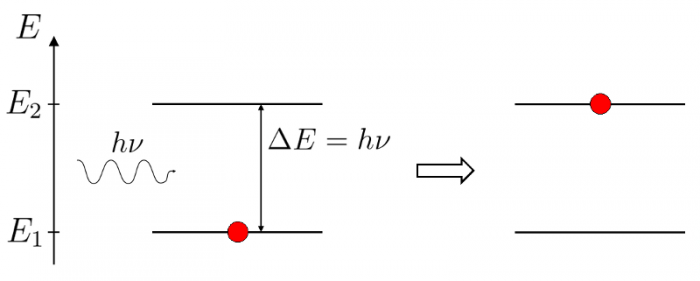
Absorption d'un photon par un système matériel possédant au moins deux niveaux d'énergie. L'énergie totale est conservée dans ce processus.
Diffusion
Lorsque la présence de matière interagit avec l'onde électromagnétique en absorbant et réémettant un photon dans un temps très court, donc sans lui soutirer d'énergie. La réémission s'effectuant dans tout l'espace, il en résulte une déviation des ondes électromagnétiques hors de la direction d'incidence. On appelle ce phénomène diffusion.
Illustration d'un processus de diffusion
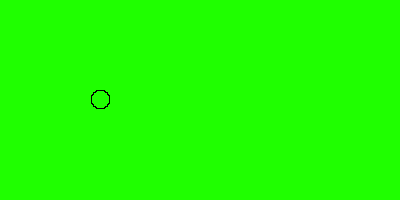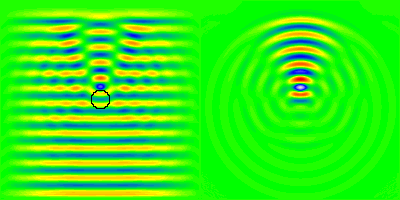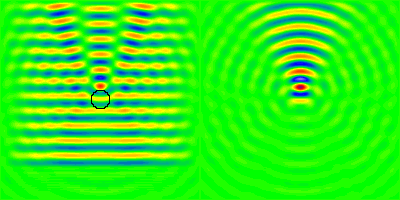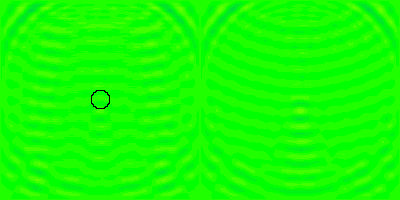
Illustration de la diffusion d'une onde électromagnétique par une sphère diélectrique de rayon comparable à la longueur d'onde et d'indice de réfraction relatif
. Le champ électrique total figure à gauche, et la composante diffusée à droite.
Crédit :
R. Hogan (Univ. of Reading)
On regroupe les phénomènes d'absorption et de diffusion sous le nom d'extinction : ces deux phénomènes ont comme point commun de diminuer l'intensité d'un faisceau lumineux dans la direction d'incidence, soit en l'absorbant, soit en en déviant tout ou partie.
Épaisseur optique / Loi de Beer-Lambert
Diffusions Rayleigh et Mie
Régimes de Rayleigh et de Mie
Le régime de diffusion Rayleigh concerne la diffusion de la lumière par des particules petites devant la longueur d'onde (rayon 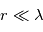 ), ce quelque soit le type d'aérosol (sphérique ou non) : molécules isolées de gaz, micro gouttes, etc.
), ce quelque soit le type d'aérosol (sphérique ou non) : molécules isolées de gaz, micro gouttes, etc.
La théorie de Mie est quant à elle valable pour toutes les valeurs de 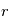 , mais uniquement pour des particules sphériques (gouttes liquides par exemple). Elle tend vers le cas Rayleigh lorsque
, mais uniquement pour des particules sphériques (gouttes liquides par exemple). Elle tend vers le cas Rayleigh lorsque 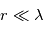 . Pour des particules non sphériques (cristaux, aérosols de Titan, poussières), cette théorie n'est valable qu'en première approximation, et les méthodes utilisées pour aller plus loin sont hors-programme.
. Pour des particules non sphériques (cristaux, aérosols de Titan, poussières), cette théorie n'est valable qu'en première approximation, et les méthodes utilisées pour aller plus loin sont hors-programme.
Section efficace de diffusion
Cette section efficace évolue de façon très différente selon le régime. Dans le régime Rayleigh, la section efficace est une fonction rapidement croissante de la longueur d'onde (une illustration courante étant la diffusion bien plus importante du bleu que de rouge dans l'atmosphère terrestre, donnant sa couleur à notre ciel). En régime de Mie, cette dépendance est bien plus faible, si bien que les diffuseurs apparaissent peu colorés en l'absence d'absorption (sur Terre, les nuages d'eau liquide sont un bon exemple).
Section efficace de diffusion
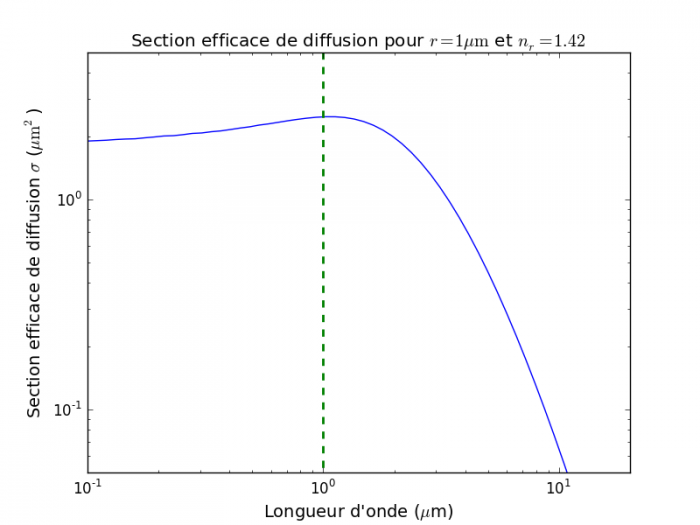
Représentation log-log de la section efficace de diffusion en fonction de la longueur d'onde pour des particules sphériques d'un rayon
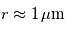
. Aux grandes longueurs d'onde,
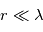
et on se trouve dans le régime
Rayleigh (
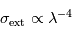
, apparaissant comme une asymptote de pente -4). Pour
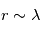
et
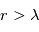
, on se trouve dans le régime de
Mie, où la section efficace est presque indépendante de
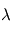
et voisine de la section géométrique des particules.
Crédit :
Loïc Rossi CC-BY-SA
Fonction de phase
La fonction de phase définit la répartition angulaire du rayonnement diffusé. C'est en quelque sorte la probabilité pour un rayon incident d'être diffusé dans une direction donnée.
Fonctions de phase de Rayleigh et de Mie

Figure montrant les indicatrices des différents processus de diffusion. La lumière incidente est supposée aller de gauche à droite. Plus la flèche est longue, plus la diffusion sera importante dans cette direction. À gauche, le régime de Rayleigh avec une diffusion relativement isotrope. Au centre, la diffusion de Mie, qui diffuse fortement vers l'avant. À droite, la diffusion de Mie pour des particules encore plus grandes.
Crédit :
Sharayanan CC-BY-SA
Surfaces
Types de réflexion
Quand du rayonnement parvient à une surface, il peut être réfléchi de plusieurs façons :
- Lambertienne, si les défauts de la surface sont supérieurs à la longueur d'onde du rayonnement incident. La lumière est alors réfléchie dans toutes les directions de façon homogène, on parle alors de surface lambertienne. Un mur blanc est un exemple de surface lambertienne ;
- Spéculaire, si les défauts sont très petits devant la longueur d'onde : la surface agit alors comme un miroir à la longueur d'onde considérée. Une surface liquide (une mer calme) peut agir comme une surface de réflexion spéculaire.
Réflexion diffuse et spéculaire

Photographie de la Terre prise depuis la station spatiale internationale. On distingue nettement la réflexion spéculaire sur la surface de l'océan et celle diffuse due aux nuages ou à la surface des continents.
Spectroscopie
Selon la longueur d'onde, le rayonnement incident sur une surface peut-être réfléchi mais aussi absorbé. On pourra alors étudier la réflectance d'une surface en fonction de la longueur d'onde (la réflectance valant 1 si tout la lumière est réfléchie ; 0 si tout est absorbé.).
L'étude de la réflectance d'une surface en fonction de la longueur d'onde peut être utile pour caractériser celle-ci. Ainsi certains minéraux ont un spectre avec des bandes d'absoption caractéristiques. C'est ce qui permet de caractériser des surfaces comme celles de Mars (pour détecter des minéraux hydratés par exemple), de la Lune ou bien celle d'astéroïdes et de comètes.
Température de brillance
Intérêt
Son intérêt principal réside dans l'interprétation des spectres thermiques issus d'un objet (ici une planète et son atmosphère). En effet, sous réserve de certaines hypothèses :
- Absence de diffusion Toute extinction du rayonnement thermique est due à son absorption.
- Absorbant uniformément mélangé et de section efficace indépendante de la pression.
- Atmosphère en équilibre hydrostatique et isotherme en géométrie plan-parallèle (courbure planétaire négligée). L'hypothèse isotherme n'est ici requise que d'un point de vue hydrostatique, pas d'un point de vue radiatif.
La température de brillance correspond alors à la température du milieu situé à une profondeur optique égale à 1 : ![T_B(\lambda) \approx T\left[\tau(\lambda) = 1\right]](../pages_flux-et-spectre/equations_trans-rad/equation41.png) avec
avec 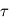 comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :
comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :
- les couches situées à des profondeurs optiques trop grandes devant 1 ne contribuent que faiblement car leur émission est trop atténuée selon la loi de Beer-Lambert.
- l'émission thermique des couches situées à faible profondeur optique est quant à elle peu atténuée, mais hélas trop peu intense pour contribuer significativement au rayonnement reçu (la loi de Kirchhoff impose que les bons émetteurs thermiques doivent aussi être de bons absorbants).
Méthodes
Auteurs: Loïc Rossi, Emmanuel Marcq
Nadir
Auteurs: Loïc Rossi, Emmanuel Marcq
Sondages thermiques
Raies en absorption vs. émission
Nous sommes à présent en mesure d'interpréter pourquoi les raies caractéristiques de certains gaz apparaissent tantôt en absorption, tantôt en émission dans les spectres thermiques observés. En effet, le centre d'une raie spectrale présente une absorption massique plus grande que les ailes de cette même raie. En conséquence, du point de vue d'un observateur extérieur à l'atmosphère, la profondeur optique unité est atteinte à des altitudes plus élevées aux centres des raies que sur leurs ailes. À partir de là, on a les cas de figure suivants :
- Lorsque le profil thermique décroît avec l'altitude (troposphère, mésosphère), les coeurs des raies atteint une profondeur optique de 1 à plus haute altitude, donc sondent un milieu de température plus faible que les ailes : les raies apparaissent alors en absorption.
- Inversement, lorsque le profil thermique croît avec l'altitude (stratosphère), les coeurs des raies sondent un milieu de température plus élevée que les ailes : les raies apparaissent alors en émission.
Raies en absorption ou en émission
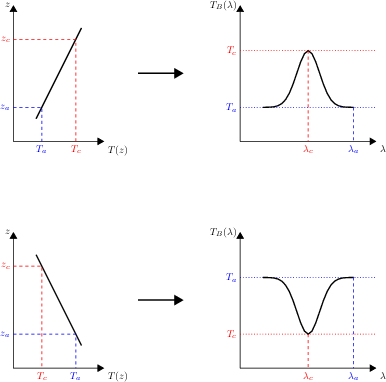
Profils d'une raie spectrale vue en émission (haut) ou en absorption (bas). L'altitude
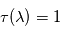
est atteinte plus haut au coeur de la raie (longueur d'onde
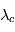
) que dans les ailes lointaines de la raie (longueur d'onde
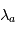
) :
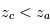
avec
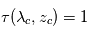
et
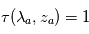
.
Crédit :
Emmanuel Marcq CC-BY-SA
Sondages de composition
Principe
Lorsque le profil vertical de température est supposé connu dans une atmosphère planétaire (par exemple au moyen de la méthode décrite précédemment), il est possible d'utiliser les raies spectrales de composés identifiés (et bien connus spectroscopiquement) pour en déduire leur profil vertical d'abondance sur une plage d'altitudes donnée.
De façon semi-quantitative et en visée nadir, on peut procéder comme suit : la connaissance du profil thermique 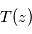 permet, pour chaque longueur d'onde
permet, pour chaque longueur d'onde 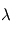 , de retrouver l'altitude
, de retrouver l'altitude 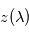 correspondant à la température de brillance observée — en d'autres termes telle que
correspondant à la température de brillance observée — en d'autres termes telle que ![T_B(\lambda) = T\left[z(\lambda)\right]](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation15.png) . Or, on sait que cette altitude correspond à la profondeur optique unité à la longueur d'onde considérée, si bien que l'on a
. Or, on sait que cette altitude correspond à la profondeur optique unité à la longueur d'onde considérée, si bien que l'on a ![\tau \left[ z(\lambda) \right] = \sigma_{\mathrm{abs}}(\lambda) \times N\left[z(\lambda) \right] = 1](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation16.png) où
où 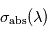 désigne la section efficace d'absorption du composé mesuré (supposée ici indépendante de la pression et de la température) et
désigne la section efficace d'absorption du composé mesuré (supposée ici indépendante de la pression et de la température) et 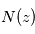 la densité de colonne du composé recherché au-dessus de l'altitude
la densité de colonne du composé recherché au-dessus de l'altitude 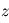 , c'est-à-dire
, c'est-à-dire 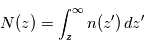 avec
avec 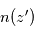 la densité volumique de l'absorbant à l'altitude
la densité volumique de l'absorbant à l'altitude 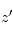 . On peut alors en déduire par différentiation sur les altitudes sondées le profil de densité volumique
. On peut alors en déduire par différentiation sur les altitudes sondées le profil de densité volumique 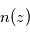 du composé mesuré sur l'intervalle sondé.
du composé mesuré sur l'intervalle sondé.
Cependant, afin de moins dépendre des diverses approximations déjà évoquées, il est préférable d'utiliser un modèle de transfert de rayonnement afin de modéliser les spectres thermiques attendus et de les comparer ensuite aux observations en ajustant les différents paramètres (opération appelée fit en anglais de laboratoire). Notons que la procédure décrite ci-dessus ne fonctionne en pratique que lorsque les raies spectrales sont résolues, c'est-à-dire à une très haute résolution spectrale.
Il n'est en revanche pas possible d'inverser simultanément le profil thermique et le profil d'abondance du composé par la seule observation de ses raies d'absorption. On parle de problème dégénéré.
Absorption de quelques gaz dans l'IR thermique
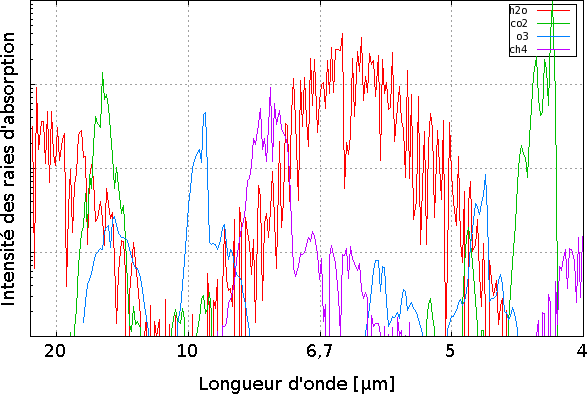
Absorption de la vapeur d'eau (rouge), du dioxyde de carbone (vert), de l'ozone (bleu) et du méthane (violet) dans les conditions standard de température et de pression. L'échelle verticale est logarithmique.
Crédit :
Emmanuel Marcq (à partir de la base de données GEISA 2011) CC-BY-SA
Spectre réfléchis
Occultations et transits
Auteurs: Loïc Rossi, Emmanuel Marcq
Occultations
 La méthode des pelures d'oignon
La méthode des pelures d'oignon
L'observation d'une occultation au cours du lever (ou du coucher) de la source à travers l'atmosphère d'une planète permet d'inverser le profil vertical d'extinction 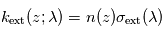 à la longueur d'onde
à la longueur d'onde 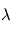 à partir de l'observation des transmissions
à partir de l'observation des transmissions 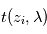 selon différentes altitudes tangentes
selon différentes altitudes tangentes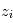 (altitude minimale du rayon lors de sa traversée de l'atmosphère). Un des algorithmes permettant cette inversion est appelé méthode des pelures d'oignon : on découpe l'atmosphère en coquilles sphériques concentriques homogènes à la manière d'un oignon. L'altitude tangente
(altitude minimale du rayon lors de sa traversée de l'atmosphère). Un des algorithmes permettant cette inversion est appelé méthode des pelures d'oignon : on découpe l'atmosphère en coquilles sphériques concentriques homogènes à la manière d'un oignon. L'altitude tangente 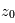 la plus élevée pour laquelle on mesure
la plus élevée pour laquelle on mesure 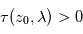 permet de déduire l'extinction locale
permet de déduire l'extinction locale 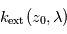 au sein de cette couche la plus extérieure. La profondeur optique observée juste en-dessous, à l'altitude tangente
au sein de cette couche la plus extérieure. La profondeur optique observée juste en-dessous, à l'altitude tangente 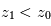 , est alors un peu plus grande. Comme on connaît déjà
, est alors un peu plus grande. Comme on connaît déjà 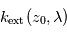 , on en déduit
, on en déduit 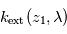 pour la couche immédiatement intérieure. Et ainsi de suite jusqu'au rayon le plus bas pour lequel on puisse mesurer une transmission
pour la couche immédiatement intérieure. Et ainsi de suite jusqu'au rayon le plus bas pour lequel on puisse mesurer une transmission 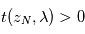 .
.
La mesure des profils d'extinction 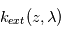 dans l'atmosphère permet alors d'en déduire plusieurs paramètres importants :
dans l'atmosphère permet alors d'en déduire plusieurs paramètres importants :
- si on connaît la section efficace d'exinction
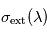 du constituant responsable de l'extinction, on peut en déduire sa densité locale
du constituant responsable de l'extinction, on peut en déduire sa densité locale 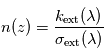 . Si, en plus, le constituant responsable de l'extinction est bien mélangé, alors on sait que son profil vertical
. Si, en plus, le constituant responsable de l'extinction est bien mélangé, alors on sait que son profil vertical 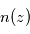 suit la loi hydrostatique, c'est-à-dire une décroissance verticale localement exponentielle selon l'échelle de hauteur atmosphérique locale
suit la loi hydrostatique, c'est-à-dire une décroissance verticale localement exponentielle selon l'échelle de hauteur atmosphérique locale 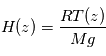 . La décroissance de
. La décroissance de 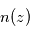 avec l'altitude nous donne alors accès à
avec l'altitude nous donne alors accès à 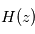 et par conséquent au profil thermique
et par conséquent au profil thermique 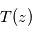 au sein des couches sondées.
au sein des couches sondées. - pour une espèce
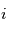 dont le rapport de mélange
dont le rapport de mélange 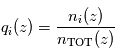 n'est pas verticalement uniforme, la mesure de son profil d'extinction
n'est pas verticalement uniforme, la mesure de son profil d'extinction 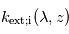 et la connaissance de sa section efficace d'extinction
et la connaissance de sa section efficace d'extinction 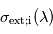 permettent d'en déduire
permettent d'en déduire 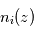 . On peut alors en déduire
. On peut alors en déduire 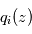 si
si 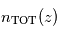 est connu par ailleurs, par exemple grâce à la mesure du profil
est connu par ailleurs, par exemple grâce à la mesure du profil 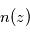 d'un constituant bien mélangé et de rapport de mélange connu.
d'un constituant bien mélangé et de rapport de mélange connu. 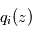 est traditionnellement exprimé en ppmv (parties volumiques par million) pour des constituants mineurs, en pourcentage volumique sinon.
est traditionnellement exprimé en ppmv (parties volumiques par million) pour des constituants mineurs, en pourcentage volumique sinon. - En dehors de l'extinction causée par les gaz, cette méthode donne aussi accès à l'extinction causée par les nuages et brumes (appelés collectivement aérosols) éventuellement présents dans l'atmosphère. Si les mesures des profils d'extinction sont faites à des longueurs d'onde assez éloignées les unes des autres, il est possible de remonter aux propriétés optiques des particules responsables de l'extinction car celles-ci varient habituellement de façon assez faible selon la longueur d'onde (contrairement par exemple aux gaz et leurs nombreuses raies spectrales). Une fois la section efficace d'extinction de ces particules ainsi contrainte, il est possible de déduire à partir des profils d'extinction mesurés le profil de densité volumique des aérosols au sein de l'atmosphère à condition de supposer ou d'avoir par ailleurs accès aux propriétés des diffuseurs individuels (forme, distribution statistique en taille, composition chimique ou au moins indices de réfraction).
Ces occultations sont donc une méthode précieuse de sondage atmosphérique, mais assez délicate à mettre en oeuvre. Il faut en effet pouvoir mesurer de nombreuses transmissions précisément, tout en connaissant parfaitement chacune des altitudes tangentes. Ceci n'est en général possible que pour un satellite en orbite autour de la planète, et nous restreint donc au système solaire.
Méthode dite "par pelure d'oignon"
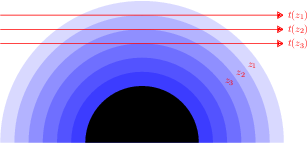
Visualisation géométrique de la méthode d'inversion surnommée "par pelure d'oignon" : la transmission observée
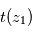
permet, connaissant l'épaisseur traversée, de remonter à
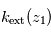
. À partir de là, la transmission
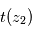
permet, connaissant
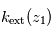
, d'en déduire
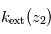
et ainsi de suite.
Crédit :
Emmanuel Marcq CC-BY-SA
Transits primaires
Transits primaires
L'observation d'un transit primaire se traduit par une baisse relative de luminosité en provenance de la source partiellement occultée, appelée profondeur du transit, notée 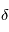 et habituellement mesurée en ppm (parties par million). Pour une planète sans atmosphère, la profondeur est indépendante de la longueur d'onde (la réciproque n'est pas vraie : ainsi un plafond nuageux élevé peut conduire à la même observation, par exemple). En revanche, si l'atmosphère présente une extinction variable selon la longueur d'onde (que ce soit par absorption ou par diffusion Rayleigh par exemple), alors le rayon apparent de la planète (et donc la profondeur du transit) sembleront légèrement plus grands dans les longueurs d'onde où l'atmosphère cause davantage d'extinction.
et habituellement mesurée en ppm (parties par million). Pour une planète sans atmosphère, la profondeur est indépendante de la longueur d'onde (la réciproque n'est pas vraie : ainsi un plafond nuageux élevé peut conduire à la même observation, par exemple). En revanche, si l'atmosphère présente une extinction variable selon la longueur d'onde (que ce soit par absorption ou par diffusion Rayleigh par exemple), alors le rayon apparent de la planète (et donc la profondeur du transit) sembleront légèrement plus grands dans les longueurs d'onde où l'atmosphère cause davantage d'extinction.
On peut ainsi montrer, sous certaines hypothèses simplificatrices, que la variation relative de la profondeur du transit selon la longueur d'onde est liée à celle de la section efficace d'extinction (moyennée verticalement) au sein de l'atmosphère, selon la loi : 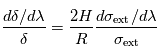 où
où 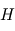 désigne l'échelle de hauteur de l'atmosphère et
désigne l'échelle de hauteur de l'atmosphère et 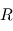 le rayon de la planète. Ces variations sont donc d'autant plus notables que l'échelle de hauteur est grande, ce qui favorise donc les atmosphères très dilatées. C'est par exemple le cas pour les Jupiter chauds (atmosphère légère constituée principalement de H2 et à température élevée).
le rayon de la planète. Ces variations sont donc d'autant plus notables que l'échelle de hauteur est grande, ce qui favorise donc les atmosphères très dilatées. C'est par exemple le cas pour les Jupiter chauds (atmosphère légère constituée principalement de H2 et à température élevée).
Spectroscopie d'un transit primaire

Visualisation de la profondeur d'un transit primaire en fonction de la longueur d'onde. Ici, l'atmosphère est transparente aux grandes longueurs d'onde, et de plus en plus opaque aux courtes longueurs d'onde, ce qui augmente la profondeur du transit.
Crédit :
Emmanuel Marcq CC-BY-SA
Transits secondaires
L'intérêt d'un transit secondaire réside dans la possibilité d'effectuer une spectroscopie différentielle de la planète : si l'on mesure un spectre 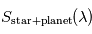 juste avant ou juste après ce transit secondaire, ainsi qu'un spectre
juste avant ou juste après ce transit secondaire, ainsi qu'un spectre 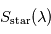 de l'étoile seule pendant ce transit secondaire, on peut en déduire le spectre
de l'étoile seule pendant ce transit secondaire, on peut en déduire le spectre 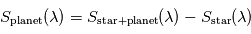 émis ou réfléchi par la planète seule vue à angle de phase nul.
émis ou réfléchi par la planète seule vue à angle de phase nul.
Le spectre 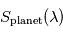 peut alors être analysé comme le serait n'importe quel spectre (par exemple en termes de température ou de composition pour un spectre thermique, ou bien de propriétés des diffuseurs pour un spectre réfléchi). C'est du moins le cas en théorie, car en pratique le faible rapport signal à bruit de tels spectres interdit à ce jour toute analyse trop poussée de ces spectres, de résolution spectrale souvent médiocre.
peut alors être analysé comme le serait n'importe quel spectre (par exemple en termes de température ou de composition pour un spectre thermique, ou bien de propriétés des diffuseurs pour un spectre réfléchi). C'est du moins le cas en théorie, car en pratique le faible rapport signal à bruit de tels spectres interdit à ce jour toute analyse trop poussée de ces spectres, de résolution spectrale souvent médiocre.
Courbe de lumière
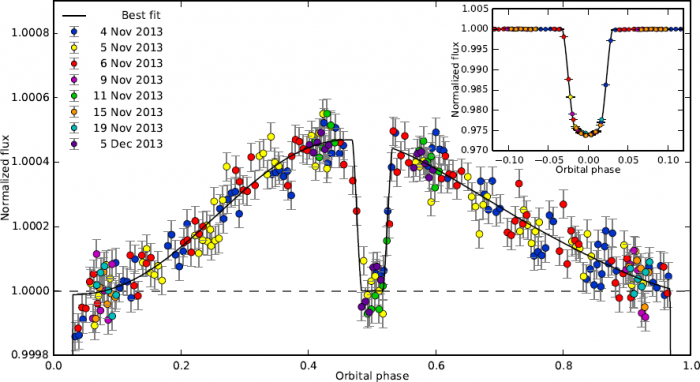
Courbe de lumière lors du transit secondaire de WASP-43b. Le flux en provenance de l'étoile est normalisé à 1. Le surcroît autour du transit secondaire est causé par l'émission thermique de la planète, ce qui a permis de reconstituer son profil thermique. L'insert en haut à droite représente le transit primaire.
Crédit :
Figure tirée de Stevenson et al. (2014)
Se Tester
Auteurs: Emmanuel Marcq, Loïc Rossi
QCM de cours
Auteur: Loïc Rossi
 Quelques questions de cours
Quelques questions de cours
Difficulté : ☆
Temps : 10 min
Transit primaire
Auteur: EM
 Étude spectroscopique d'un transit primaire
Étude spectroscopique d'un transit primaire
Difficulté : ☆☆☆
Temps : 30 min
On considère la variation avec la longueur d'onde 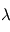 de la profondeur
de la profondeur 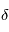 d'un transit primaire autour d'une étoile de rayon
d'un transit primaire autour d'une étoile de rayon 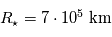 . Le meilleur ajustement par un modèle simple est représenté ci-dessous (l'axe des abscisses des gradué de façon logarithmique). L'échelle de hauteur de l'atmosphère de l'exoplanète sera supposée constante.
. Le meilleur ajustement par un modèle simple est représenté ci-dessous (l'axe des abscisses des gradué de façon logarithmique). L'échelle de hauteur de l'atmosphère de l'exoplanète sera supposée constante.
Profondeur optique vs. longueur d'onde
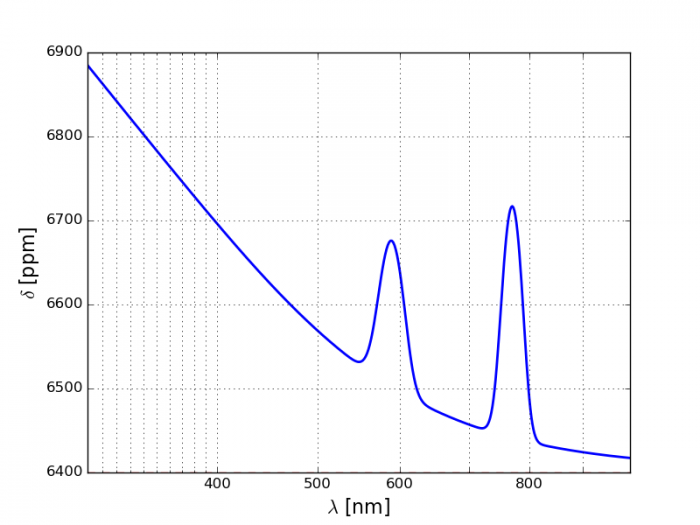
Simulation d'un transit primaire
Crédit :
EM
Question 1)
Estimer la profondeur du transit en l'absence d'atmosphère.
L'atmosphère ajoute-t-elle ou enlève-t-elle de la profondeur au transit ?
Vers quelle valeur extrémale cette profondeur tend-elle ?
Question 2)
En déduire le rayon 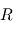 de la planète.
de la planète.
Estimer la proportion du disque stellaire obscurcie par celui de la planète.
Question 3)
Interpréter l'allure générale du spectre de 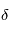 :
:
- Quel phénomène peut causer les pics isolés vers 600 et 800 nm ?
- Quel phénomène est responsable de l'augmentation constatée vers les courtes longueurs d'onde
La forme étroite de ces pics, ainsi que leur localisation donne une indication précieuse.
La pente constante peut s'interpréter au moyen d'une formule du cours, en considérant que 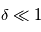
Question 4)
Mesurer la pente 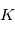 observée pour les courtes longueurs d'onde.
observée pour les courtes longueurs d'onde.
Prendre deux points faciles à repérer sur le graphique.
Sondage thermique
Auteur: EM
 Spectres d'émission thermique
Spectres d'émission thermique
Difficulté : ☆☆☆
Temps : 30 min
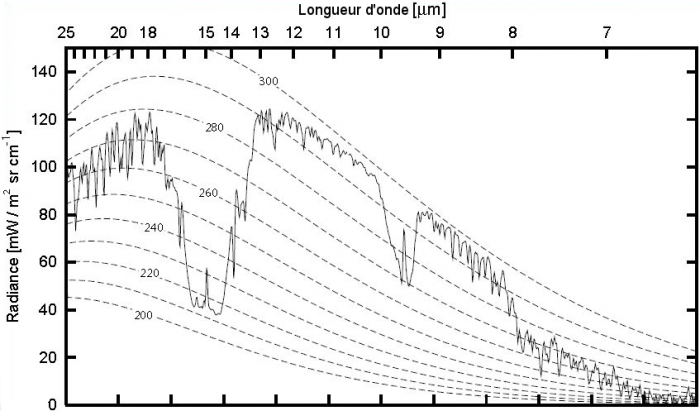
Interpréter les spectres d'émission thermiques suivants à l'aide du cours. On répondra notamment aux questions suivantes :
Pour l'interprétation du spectre 2, voici une formule semi-numérique pour convertir les radiances spectrales en température de brillance : 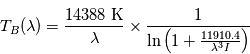 où la longueur d'onde
où la longueur d'onde 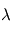 est en µm et la radiance
est en µm et la radiance 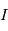 en
en 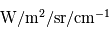
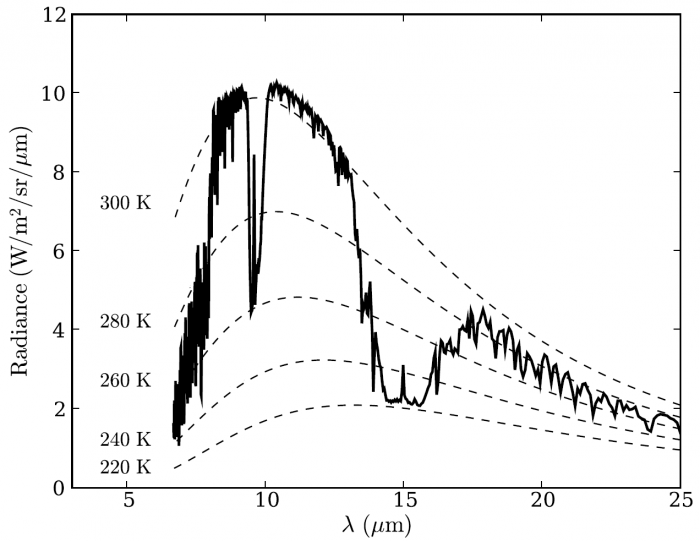
Spectre 1
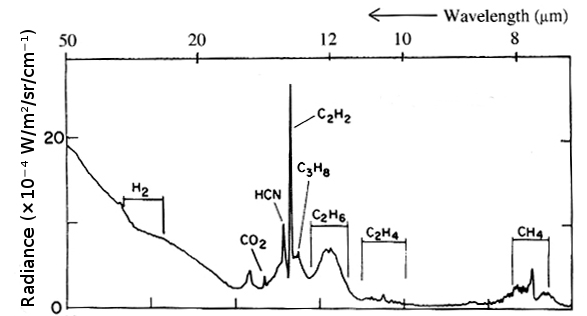
Spectre 2
Question 1)
Identifier les espèces gazeuses présentes dans la planète du spectre 1.
Il y a trois bandes identifiables.
Elles sont situées vers 15 µm, 9,6 µm et en dessous de 6 µm.
Question 2)
Estimer la température de surface pour le spectre 1, et la structure thermique des deux atmosphères.
Interpréter le spectre 1 en termes de température de brillance.
Examiner ensuite si les raies sont visibles en absorption ou en émission.
Question 3)
Interpréter les pics centraux au coeur des bandes d'absorption vers 9,6 µm et 15 µm sur le spectre 1.
Quelles altitudes sont sondées par les ailes lointaines ? les ailes proches ? le coeur des raies ?
Question 4)
Identifier les deux objets du système solaire en question.
Utilisez les réponses aux questions précendentes : température, composition, structure thermique.
Mini-projet
Auteurs: Loïc Rossi, Emmanuel Marcq
Occultation stellaire à travers l'atmosphère de Vénus
 Contexte
Contexte
En 2011, l'équipe de Franck Montmessin (LATMOS, France) a découvert l'existence d'une couche d'ozone (O3) dans la haute atmosphère de Vénus côté nuit. Cette couche est très ténue et d'extension verticale restreinte. Elle présente également d'importantes variations horizontales, pouvant passer sous le seuil de détection. Les données utilisées provenaient de l'instrument SPICAV à bord de la sonde Venus Express (2006-2014) de l'ESA, et utilisaient la méthode des occultations stellaires en ultraviolet, domaine spectral où l'ozone présente une absorption caractéristique.
Ce mini-projet se propose d'appliquer la même méthode à des occultations stellaires simulées, comparables à celle mesurées par SPICAV mais plus faciles à traiter.
 Description des occultations simulées
Description des occultations simulées
Les occultations simulées prennent en compte l'extinction de la lumière de l'étoile causée par la traversée d'une partie de l'atmosphère de Vénus. Cette atmosphère simulée est constituée de dioxyde de carbone (CO2 à 96,5%) suivant une distribution hydrostatique, et d'une couche d'ozone (O3) d'altitude fixe et d'épaisseur caractéristique assez mince. Le dioxyde de carbone absorbe majoritairement aux courtes longueurs d'onde, tandis que l'ozone présente une bande d'absorption centrée sur une longueur d'onde d'environ 250 nm (bande de Hartley) . Ce modèle, par souci de simplicité pédagogique, ne prend pas en compte les phénomènes suivants :
- les inhomogénéités horizontales : l'atmosphère est constituée de "coquilles sphériques" considérées homogènes ;
- l'extinction supplémentaire causée par les brumes normalement présentes dans la haute atmosphère de Vénus ;
- la réfraction atmosphérique, qui entraîne une déviation de la direction du rayon lors de la traversée de l'atmosphère (d'indice de réfraction variable et très légèrement supérieur à 1).
Ces occultations ont été simulées pour diverses altitudes tangentes du rayon lumineux. Ces altitudes représentent l'altitude minimale atteinte par le rayon lorsqu'il passe au plus près de Vénus. Un bruit synthétique a été également été ajouté.
 Consignes
Consignes
- Pour chaque observation, ajuster la densité de colonne d'ozone donnant le meilleur accord entre transmission théorique et observée. Copier chaque couple de valeurs vers le tableur.
- Pourquoi la transmission théorique ne réussit-elle pas à ajuster les observations aux courtes longueurs d'onde ? Interpréter le désaccord constaté, notamment vis-à-vis l'altitude tangente.
- Interpréter la courbe donnant la densité de colonne d'ozone traversée en fonction de l'altitude tangente : vérifier notamment qu'elle est compatible avec une couche mince d'ozone située à une altitude
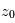 que l'on précisera.
que l'on précisera. - Représenter schématiquement trois occultations d'altitudes tangentes
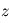 telles que :
telles que : 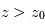 ,
, 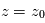 ,
, 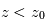 . Vérifiez la cohérence avec les variations de la densité de colonne d'ozone observées le long de ces rayons.
. Vérifiez la cohérence avec les variations de la densité de colonne d'ozone observées le long de ces rayons. - Estimer à partir du profil vertical de densité de colonne d'ozone l'épaisseur caractéristique
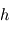 de la couche d'ozone.
de la couche d'ozone. - En considérant un modèle simplifié où l'ozone est uniformément réparti entre les altitudes
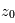 et
et 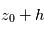 , montrer que la longueur
, montrer que la longueur 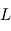 parcourue par le rayon d'altitude tangente
parcourue par le rayon d'altitude tangente 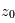 est donnée par
est donnée par 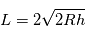 où
où 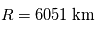 désigne le rayon de Vénus. On se placera dans l'hypothèse, vérifiée ici, où
désigne le rayon de Vénus. On se placera dans l'hypothèse, vérifiée ici, où 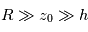 .
. - En déduire alors une estimation de la densité particulaire (en molécules/m3) d'ozone au sein de cette couche dans le cadre de ce modèle simplifié.
Simulation d'une occultation stellaire à travers l'atmosphère de Vénus
-------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------
ACCES AU PLAN DES CHAPITRES
Réponses aux QCM
pages_tester/qcm.html
QCM
'Quelques questions de cours'
- Question 1
Aide :
Penser à appliquer la loi de Beer-Lambert.
Solution : réponse 3)
- Question 2
Aide :
Référez-vous à la loi de Wien.
Solution : réponse 2)
(
En ce cas, les maxima des deux composantes tendent l'un vers l'autre, ce qui rend la distinction caduque.
)
- Question 3
Aide :
Se référer aux pages du cours à propos de la composante stellaire réfléchie ou de la composante d'émission thermique.
Solution : réponse 1)
(
Les couches situées à des profondeurs optiques grandes devant l'unité restent inacessibles, tant par leur émission thermique propre que stellaire réfléchie.
)
- Question 4
Aide :
Se reférer au cours
Solution : réponse 2)
- Question 5
Aide :
Attention au sens des implications logiques !
Solution : réponse 3)
(
Si la planète possède des nuages optiquement épais, la planète peut sembler avoir le même diamètre apparent à plusieurs longueurs d'onde, et donc avoir une profondeur de transit similaire à celle d'une planète sans atmosphère.
)
Réponses aux exercices
pages_flux-et-spectre/exo-transit.html
Exercice
'Étude spectroscopique d'un transit primaire'
- Question 1
Aide :
L'atmosphère ajoute-t-elle ou enlève-t-elle de la profondeur au transit ?
Aide :
Vers quelle valeur extrémale cette profondeur tend-elle ?
Solution :
L'atmosphère est de moins en moins opaque vers les grandes longueurs d'onde. On tend alors vers une valeur 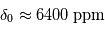 .
.
- Question 2
Aide :
Estimer la proportion du disque stellaire obscurcie par celui de la planète.
Solution :
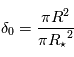 , d'où
, d'où 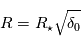 . L'application numérique donne
. L'application numérique donne 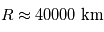 , soit une planète de taille intermédiaire entre Jupiter et Neptune.
, soit une planète de taille intermédiaire entre Jupiter et Neptune.
- Question 3
Aide :
La forme étroite de ces pics, ainsi que leur localisation donne une indication précieuse.
Aide :
La pente constante peut s'interpréter au moyen d'une formule du cours, en considérant que 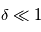
Solution :
- Il s'agit de raies spectrales causées par des éléments gazeux. Un atlas spectroscopique permettrait de déterminer qu'il s'agit de sodium (Na) vers 589 nm, et de potassium (K) vers 767 nm.
- La formule du cours donne au premier ordre :
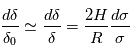 , d'où l'on tire
, d'où l'on tire 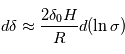 . La pente constante en
. La pente constante en 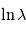 se traduit donc par
se traduit donc par 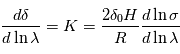 . Ceci n'est possible que si
. Ceci n'est possible que si 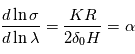 est constante, c'est-à-dire si
est constante, c'est-à-dire si 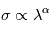 . Le phénomène le plus vraisembable est alors la diffusion Rayleigh causée par les molécules gazeuses. En ce cas,
. Le phénomène le plus vraisembable est alors la diffusion Rayleigh causée par les molécules gazeuses. En ce cas, 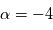 .
.
- Question 4
Aide :
Prendre deux points faciles à repérer sur le graphique.
Solution :
On trouve 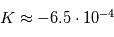 . Ne pas oublier que
. Ne pas oublier que 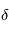 est en ppm ! (
est en ppm ! (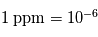 )
)
- Question 5
Aide :
Utiliser les formules des questions précédentes.
Solution :
On a 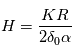 avec les notations précédentes, d'où
avec les notations précédentes, d'où 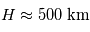 . Cela donne une température atmosphérique d'environ
. Cela donne une température atmosphérique d'environ 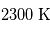 . Notons qu'une telle détermination est en pratique très imprécise, et donc d'intérêt limité.
. Notons qu'une telle détermination est en pratique très imprécise, et donc d'intérêt limité.
pages_flux-et-spectre/exo-thermique.html
Exercice
'Spectres d'émission thermique'
- Question 1
Aide :
Il y a trois bandes identifiables.
Aide :
Elles sont situées vers 15 µm, 9,6 µm et en dessous de 6 µm.
Solution :
Il s'agit de CO2 vers 15 µm, de O3 vers 9,6 µm et de H2O en-dessous de 6 µm.
- Question 2
Aide :
Interpréter le spectre 1 en termes de température de brillance.
Aide :
Examiner ensuite si les raies sont visibles en absorption ou en émission.
Solution :
Sur le spectre 1, en dehors de toute absorption gazeuse, le spectre thermique culmine à des températures de brillance légèrement supérieures à 300 K. Cela correspond à la température de surface.
Le spectre 1 présente des raies en absorption. Elles sont donc formées dans une zone où le profil thermique décroît avec l'altitude, entre environ 300 K et un minimum légèrement supérieur à 220 K. Le spectre 2, quant à lui, présente des raies d'émission, qui sont donc formées dans une stratosphère où le profil thermique croît avec l'altitude entre environ 100 K et 130 K.
- Question 3
Aide :
Quelles altitudes sont sondées par les ailes lointaines ? les ailes proches ? le coeur des raies ?
Solution :
Il s'agit de raies formées entre une zone profonde où la température décroît avec l'altitude jusque vers 220 K, et une zone plus élevée où la température remonte jusqu'à une valeur de 260 K en moins.
- Question 4
Aide :
Utilisez les réponses aux questions précendentes : température, composition, structure thermique.
Solution :
Le spectre 1 a été observé dans une atmosphère comportant du CO2, de l'ozone et du méthane. La température décroît d'une surface à environ 300 K jusqu'à un minimum de 220 K (troposphère), avant de croître à nouveau jusque vers 260 K (une stratosphère). Dans le système solaire, cela correspond à la Terre (plus précisément au-dessus d'un désert tropical).
Le spectre 2 a été quant à lui observé dans une atmosphère froide (température de brillance n'excédant pas 130 K), comportant une stratosphère et de nombreux composés organiques (hydrocarbures, nitriles). Dans le système solaire, cela correspond à Titan, satellite de Saturne.
 Objectifs
Objectifs Prérequis
Prérequis










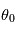 (SZA, pour Solar Zenith Angle) : c'est l'angle entre la direction du zénith et la direction du Soleil ;
(SZA, pour Solar Zenith Angle) : c'est l'angle entre la direction du zénith et la direction du Soleil ;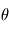 (EMI) : c'est l'angle entre la direction du zénith et celle du rayon émergent/diffusé ;
(EMI) : c'est l'angle entre la direction du zénith et celle du rayon émergent/diffusé ; 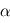 : c'est l'angle entre la direction du Soleil et la direction de l'observateur.
: c'est l'angle entre la direction du Soleil et la direction de l'observateur.
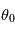 est l'angle solaire zénithal (SZA) ; en vert
est l'angle solaire zénithal (SZA) ; en vert 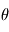 est l'angle d'émission (EMI) ; et en rouge l'angle
est l'angle d'émission (EMI) ; et en rouge l'angle 

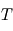 (on peut voir alors leur interaction comme celle d'un gaz de photons perpétuellement absorbés et émis par la matière environnante, et se mettant en équilibre de la sorte). Il existe également des phénomènes d'émission non thermiques (ex: fluorescence, émission laser), mais ils sortent du cadre de ce cours ; certains de ces processus sont vus dans
(on peut voir alors leur interaction comme celle d'un gaz de photons perpétuellement absorbés et émis par la matière environnante, et se mettant en équilibre de la sorte). Il existe également des phénomènes d'émission non thermiques (ex: fluorescence, émission laser), mais ils sortent du cadre de ce cours ; certains de ces processus sont vus dans 

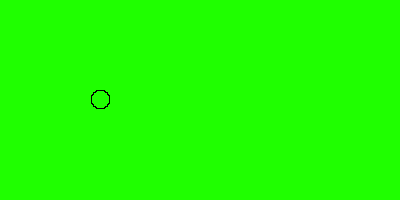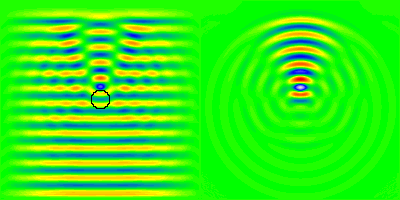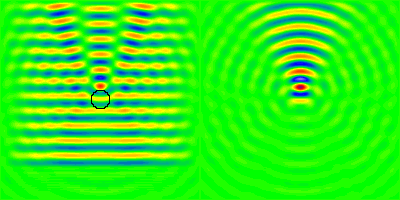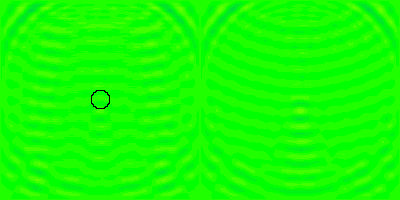
 . Le champ électrique total figure à gauche, et la composante diffusée à droite.
. Le champ électrique total figure à gauche, et la composante diffusée à droite.
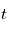 comme le rapport entre l'intensité lumineuse
comme le rapport entre l'intensité lumineuse 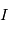 après traversée et celle
après traversée et celle 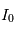 avant la traversée du milieu :
avant la traversée du milieu : 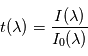 . Cette transmittance vaut 1 si le milieu traversé est transparent, 0 si le milieu est parfaitement opaque, et prend une valeur intermédiaire si le milieu est partiellement opaque. Elle dépend a priori de la longueur d'onde comme la formule l'indique.
. Cette transmittance vaut 1 si le milieu traversé est transparent, 0 si le milieu est parfaitement opaque, et prend une valeur intermédiaire si le milieu est partiellement opaque. Elle dépend a priori de la longueur d'onde comme la formule l'indique.
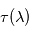 qui se déduit de la transmittance comme suit :
qui se déduit de la transmittance comme suit : ![\tau(\lambda) = - \ln \left[ t(\lambda) \right]](../pages_flux-et-spectre/equations_trans-rad/equation8.png) , soit
, soit 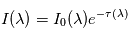 . Il est alors facile de déduire des propriétés mathématiques du logarithme que
. Il est alors facile de déduire des propriétés mathématiques du logarithme que 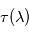 est une grandeur additive le long d'un même rayon (voir figure ci-contre), et qu'elle offre donc un paramétrage naturel de l'abscisse curviligne le long de ce rayon. Il est en outre possible de relier physiquement la variation locale de
est une grandeur additive le long d'un même rayon (voir figure ci-contre), et qu'elle offre donc un paramétrage naturel de l'abscisse curviligne le long de ce rayon. Il est en outre possible de relier physiquement la variation locale de 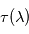 le long d'un rayon à la présence de matière traversée : c'est la loi de Beer-Lambert .
le long d'un rayon à la présence de matière traversée : c'est la loi de Beer-Lambert .
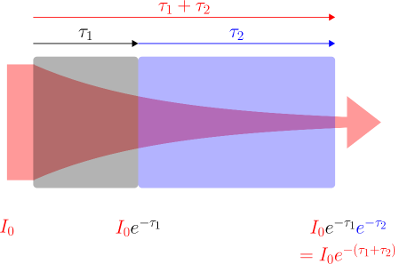
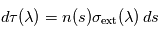 où
où 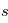 désigne l'abscisse curviligne le long du rayon (croissant dans le sens de propagation),
désigne l'abscisse curviligne le long du rayon (croissant dans le sens de propagation), 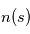 la densité volumique de diffusants et/ou absorbants et
la densité volumique de diffusants et/ou absorbants et 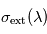 la section efficace d'extinction des diffusants et/ou absorbants. En présence de plusieurs types de diffuseurs et/ou d'absorbeurs, il suffit d'ajouter leurs contributions individuelles. L'évolution de la profondeur optique totale
la section efficace d'extinction des diffusants et/ou absorbants. En présence de plusieurs types de diffuseurs et/ou d'absorbeurs, il suffit d'ajouter leurs contributions individuelles. L'évolution de la profondeur optique totale 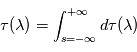 selon la longueur d'onde au cours d'une occultation ou d'un transit offre donc la possibilité à l'observateur de déduire les propriétés matérielles du milieu traversé (densité volumique et nature physique des particules responsables de l'extinction).
selon la longueur d'onde au cours d'une occultation ou d'un transit offre donc la possibilité à l'observateur de déduire les propriétés matérielles du milieu traversé (densité volumique et nature physique des particules responsables de l'extinction).
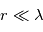 ), ce quelque soit le type d'aérosol (sphérique ou non) : molécules isolées de gaz, micro gouttes, etc.
), ce quelque soit le type d'aérosol (sphérique ou non) : molécules isolées de gaz, micro gouttes, etc.
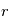 , mais uniquement pour des particules sphériques (gouttes liquides par exemple). Elle tend vers le cas Rayleigh lorsque
, mais uniquement pour des particules sphériques (gouttes liquides par exemple). Elle tend vers le cas Rayleigh lorsque 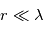 . Pour des particules non sphériques (cristaux, aérosols de Titan, poussières), cette théorie n'est valable qu'en première approximation, et les méthodes utilisées pour aller plus loin sont hors-programme.
. Pour des particules non sphériques (cristaux, aérosols de Titan, poussières), cette théorie n'est valable qu'en première approximation, et les méthodes utilisées pour aller plus loin sont hors-programme.

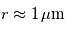 . Aux grandes longueurs d'onde,
. Aux grandes longueurs d'onde, 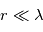 et on se trouve dans le régime Rayleigh (
et on se trouve dans le régime Rayleigh (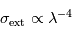 , apparaissant comme une asymptote de pente -4). Pour
, apparaissant comme une asymptote de pente -4). Pour 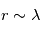 et
et 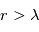 , on se trouve dans le régime de Mie, où la section efficace est presque indépendante de
, on se trouve dans le régime de Mie, où la section efficace est presque indépendante de 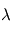 et voisine de la section géométrique des particules.
et voisine de la section géométrique des particules.

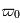 comme la proportion du rayonnement qui est diffusée. Si
comme la proportion du rayonnement qui est diffusée. Si 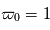 , toute la lumière est diffusée, il n'y a pas d'absorption. En revanche si
, toute la lumière est diffusée, il n'y a pas d'absorption. En revanche si 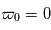 , tout la lumière est absorbée, il n'y a plus de diffusion. En général,
, tout la lumière est absorbée, il n'y a plus de diffusion. En général, 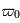 dépend de la longueur d'onde :
dépend de la longueur d'onde : 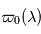 .
.

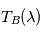 d'un objet est la température du corps noir qui émettrait la même intensité que celle émise par l'objet à la longueur d'onde
d'un objet est la température du corps noir qui émettrait la même intensité que celle émise par l'objet à la longueur d'onde 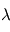 :
: ![I(\lambda) = B\left[\lambda, T_B(\lambda) \right]](../pages_flux-et-spectre/equations_trans-rad/equation33.png) où
où ![B\left[\lambda, T \right]](../pages_flux-et-spectre/equations_trans-rad/equation34.png) désigne la fonction de Planck à la longueur d'onde
désigne la fonction de Planck à la longueur d'onde 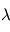 pour un corps noir de température
pour un corps noir de température 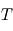 . Comme les courbes représentant les fonctions de Planck ne se croisent jamais, il y a correspondance unique entre
. Comme les courbes représentant les fonctions de Planck ne se croisent jamais, il y a correspondance unique entre 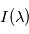 et
et 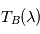 : la température de brillance n'est qu'une autre façon de décrire un spectre. En particulier, elle ne représente pas forcément la température d'un objet physique.
: la température de brillance n'est qu'une autre façon de décrire un spectre. En particulier, elle ne représente pas forcément la température d'un objet physique.
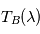 selon la formule
selon la formule 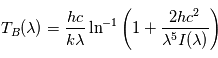 .
.
![T_B(\lambda) \approx T\left[\tau(\lambda) = 1\right]](../pages_flux-et-spectre/equations_trans-rad/equation41.png) avec
avec 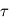 comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :
comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :

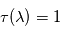 est atteinte plus haut au coeur de la raie (longueur d'onde
est atteinte plus haut au coeur de la raie (longueur d'onde 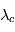 ) que dans les ailes lointaines de la raie (longueur d'onde
) que dans les ailes lointaines de la raie (longueur d'onde 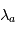 ) :
) : 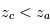 avec
avec 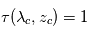 et
et 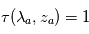 .
.
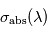 et le profil vertical en densité de l'absorbant
et le profil vertical en densité de l'absorbant 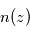 sont connus, il est alors possible de trouver à quelle altitude
sont connus, il est alors possible de trouver à quelle altitude 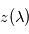 on a
on a ![\tau \left[ z(\lambda) \right] = \int_{z(\lambda)}^{+\infty} \sigma_{\mathrm{abs}}(\lambda) n(z')\,dz' = 1](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation10.png) . On sait alors qu'il règne une température
. On sait alors qu'il règne une température ![T\left[ z(\lambda) \right] \approx T_B(\lambda)](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation11.png) à cette altitude. On a supposé dans ce calcul que la visée de l'observateur pointe verticalement vers le centre de la planète (visée nadir).
à cette altitude. On a supposé dans ce calcul que la visée de l'observateur pointe verticalement vers le centre de la planète (visée nadir).
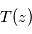 permet, pour chaque longueur d'onde
permet, pour chaque longueur d'onde 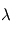 , de retrouver l'altitude
, de retrouver l'altitude 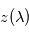 correspondant à la température de brillance observée — en d'autres termes telle que
correspondant à la température de brillance observée — en d'autres termes telle que ![T_B(\lambda) = T\left[z(\lambda)\right]](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation15.png) . Or, on sait que cette altitude correspond à la profondeur optique unité à la longueur d'onde considérée, si bien que l'on a
. Or, on sait que cette altitude correspond à la profondeur optique unité à la longueur d'onde considérée, si bien que l'on a ![\tau \left[ z(\lambda) \right] = \sigma_{\mathrm{abs}}(\lambda) \times N\left[z(\lambda) \right] = 1](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation16.png) où
où 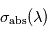 désigne la section efficace d'absorption du composé mesuré (supposée ici indépendante de la pression et de la température) et
désigne la section efficace d'absorption du composé mesuré (supposée ici indépendante de la pression et de la température) et 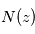 la densité de colonne du composé recherché au-dessus de l'altitude
la densité de colonne du composé recherché au-dessus de l'altitude 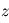 , c'est-à-dire
, c'est-à-dire 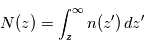 avec
avec 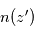 la densité volumique de l'absorbant à l'altitude
la densité volumique de l'absorbant à l'altitude 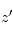 . On peut alors en déduire par différentiation sur les altitudes sondées le profil de densité volumique
. On peut alors en déduire par différentiation sur les altitudes sondées le profil de densité volumique 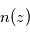 du composé mesuré sur l'intervalle sondé.
du composé mesuré sur l'intervalle sondé.

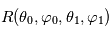 appelée réflectance bidirectionnelle. C'est une fonction à quatre variables, deux pour caractériser la direction du rayon incident (d'angle zénital d'incidence
appelée réflectance bidirectionnelle. C'est une fonction à quatre variables, deux pour caractériser la direction du rayon incident (d'angle zénital d'incidence 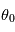 et d'azimuth
et d'azimuth 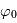 ) et deux pour celle du rayon émergent (d'angle d'émergence zénital
) et deux pour celle du rayon émergent (d'angle d'émergence zénital 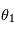 et d'azimuth
et d'azimuth 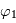 ) . C'est une fonction positive, dont la valeur minimale est nulle dans les directions où l'intensité réfléchie est nulle. Elle ne se déduit pas simplement des fonctions de phase calculables en régime de Rayleigh et de Mie, notamment à cause des phénomènes de diffusion multiple et de la possible contibution de la surface.
) . C'est une fonction positive, dont la valeur minimale est nulle dans les directions où l'intensité réfléchie est nulle. Elle ne se déduit pas simplement des fonctions de phase calculables en régime de Rayleigh et de Mie, notamment à cause des phénomènes de diffusion multiple et de la possible contibution de la surface.
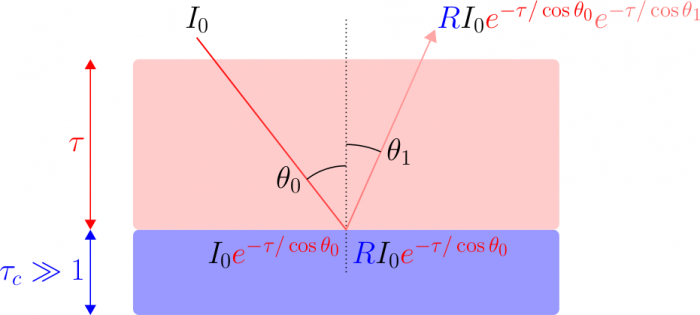
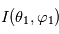 et celle de la source
et celle de la source 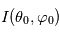 :
: ![I(\theta_1,\varphi_1) = I(\theta_0,\varphi_0) R(\theta_0,\varphi_0,\theta_1,\varphi_1) \exp \left[ - \tau \left(\frac{1}{\cos \theta_0} + \frac{1}{\cos \theta_1} \right) \right]](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation31.png) où
où 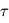 désigne l'épaisseur optique de l'atmosphère au-dessus de la couche réfléchissante (comptée selon la verticale). Le terme en exponentielle provient de la loi de Beer-Lambert pour le rayon incident et le rayon émergent, en tenant compte de leur inclinaison éventuelle qui les amène à traverser des épaisseurs atmosphériques plus importantes que des rayons purement verticaux.
désigne l'épaisseur optique de l'atmosphère au-dessus de la couche réfléchissante (comptée selon la verticale). Le terme en exponentielle provient de la loi de Beer-Lambert pour le rayon incident et le rayon émergent, en tenant compte de leur inclinaison éventuelle qui les amène à traverser des épaisseurs atmosphériques plus importantes que des rayons purement verticaux.
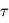 est négligeable, cette méthode permet de mesurer le spectre de l'absorption atmosphérique décrite par
est négligeable, cette méthode permet de mesurer le spectre de l'absorption atmosphérique décrite par 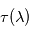 : on a ainsi accès à la densité de colonne intégrée au-dessus de la couche réfléchissante en examinant la profondeur des raies d'absorption des composés atmosphériques. Notons qu'au contraire de l'émission thermique, la présence de composés absorbants se traduit toujours par des raies en absorption et non plus en émission.
: on a ainsi accès à la densité de colonne intégrée au-dessus de la couche réfléchissante en examinant la profondeur des raies d'absorption des composés atmosphériques. Notons qu'au contraire de l'émission thermique, la présence de composés absorbants se traduit toujours par des raies en absorption et non plus en émission.
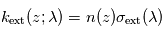 à la longueur d'onde
à la longueur d'onde 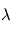 à partir de l'observation des transmissions
à partir de l'observation des transmissions 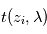 selon différentes altitudes tangentes
selon différentes altitudes tangentes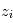 (altitude minimale du rayon lors de sa traversée de l'atmosphère). Un des algorithmes permettant cette inversion est appelé méthode des pelures d'oignon : on découpe l'atmosphère en coquilles sphériques concentriques homogènes à la manière d'un oignon. L'altitude tangente
(altitude minimale du rayon lors de sa traversée de l'atmosphère). Un des algorithmes permettant cette inversion est appelé méthode des pelures d'oignon : on découpe l'atmosphère en coquilles sphériques concentriques homogènes à la manière d'un oignon. L'altitude tangente 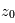 la plus élevée pour laquelle on mesure
la plus élevée pour laquelle on mesure 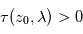 permet de déduire l'extinction locale
permet de déduire l'extinction locale 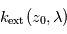 au sein de cette couche la plus extérieure. La profondeur optique observée juste en-dessous, à l'altitude tangente
au sein de cette couche la plus extérieure. La profondeur optique observée juste en-dessous, à l'altitude tangente 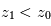 , est alors un peu plus grande. Comme on connaît déjà
, est alors un peu plus grande. Comme on connaît déjà 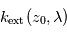 , on en déduit
, on en déduit 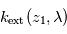 pour la couche immédiatement intérieure. Et ainsi de suite jusqu'au rayon le plus bas pour lequel on puisse mesurer une transmission
pour la couche immédiatement intérieure. Et ainsi de suite jusqu'au rayon le plus bas pour lequel on puisse mesurer une transmission 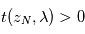 .
.
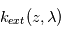 dans l'atmosphère permet alors d'en déduire plusieurs paramètres importants :
dans l'atmosphère permet alors d'en déduire plusieurs paramètres importants :
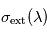 du constituant responsable de l'extinction, on peut en déduire sa densité locale
du constituant responsable de l'extinction, on peut en déduire sa densité locale 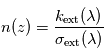 . Si, en plus, le constituant responsable de l'extinction est bien mélangé, alors on sait que son profil vertical
. Si, en plus, le constituant responsable de l'extinction est bien mélangé, alors on sait que son profil vertical 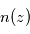 suit la loi hydrostatique, c'est-à-dire une décroissance verticale localement exponentielle selon l'échelle de hauteur atmosphérique locale
suit la loi hydrostatique, c'est-à-dire une décroissance verticale localement exponentielle selon l'échelle de hauteur atmosphérique locale 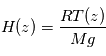 . La décroissance de
. La décroissance de 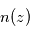 avec l'altitude nous donne alors accès à
avec l'altitude nous donne alors accès à 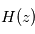 et par conséquent au profil thermique
et par conséquent au profil thermique 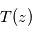 au sein des couches sondées.
au sein des couches sondées.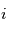 dont le rapport de mélange
dont le rapport de mélange 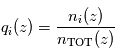 n'est pas verticalement uniforme, la mesure de son profil d'extinction
n'est pas verticalement uniforme, la mesure de son profil d'extinction 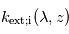 et la connaissance de sa section efficace d'extinction
et la connaissance de sa section efficace d'extinction 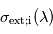 permettent d'en déduire
permettent d'en déduire 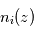 . On peut alors en déduire
. On peut alors en déduire 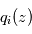 si
si 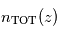 est connu par ailleurs, par exemple grâce à la mesure du profil
est connu par ailleurs, par exemple grâce à la mesure du profil 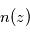 d'un constituant bien mélangé et de rapport de mélange connu.
d'un constituant bien mélangé et de rapport de mélange connu. 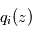 est traditionnellement exprimé en ppmv (parties volumiques par million) pour des constituants mineurs, en pourcentage volumique sinon.
est traditionnellement exprimé en ppmv (parties volumiques par million) pour des constituants mineurs, en pourcentage volumique sinon.
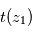 permet, connaissant l'épaisseur traversée, de remonter à
permet, connaissant l'épaisseur traversée, de remonter à 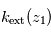 . À partir de là, la transmission
. À partir de là, la transmission 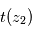 permet, connaissant
permet, connaissant 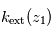 , d'en déduire
, d'en déduire 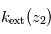 et ainsi de suite.
et ainsi de suite.
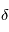 et habituellement mesurée en ppm (parties par million). Pour une planète sans atmosphère, la profondeur est indépendante de la longueur d'onde (la réciproque n'est pas vraie : ainsi un plafond nuageux élevé peut conduire à la même observation, par exemple). En revanche, si l'atmosphère présente une extinction variable selon la longueur d'onde (que ce soit par absorption ou par diffusion Rayleigh par exemple), alors le rayon apparent de la planète (et donc la profondeur du transit) sembleront légèrement plus grands dans les longueurs d'onde où l'atmosphère cause davantage d'extinction.
et habituellement mesurée en ppm (parties par million). Pour une planète sans atmosphère, la profondeur est indépendante de la longueur d'onde (la réciproque n'est pas vraie : ainsi un plafond nuageux élevé peut conduire à la même observation, par exemple). En revanche, si l'atmosphère présente une extinction variable selon la longueur d'onde (que ce soit par absorption ou par diffusion Rayleigh par exemple), alors le rayon apparent de la planète (et donc la profondeur du transit) sembleront légèrement plus grands dans les longueurs d'onde où l'atmosphère cause davantage d'extinction.
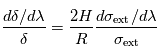 où
où 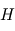 désigne l'
désigne l'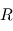 le rayon de la planète. Ces variations sont donc d'autant plus notables que l'échelle de hauteur est grande, ce qui favorise donc les atmosphères très dilatées. C'est par exemple le cas pour les Jupiter chauds (atmosphère légère constituée principalement de H2 et à température élevée).
le rayon de la planète. Ces variations sont donc d'autant plus notables que l'échelle de hauteur est grande, ce qui favorise donc les atmosphères très dilatées. C'est par exemple le cas pour les Jupiter chauds (atmosphère légère constituée principalement de H2 et à température élevée).

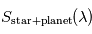 juste avant ou juste après ce transit secondaire, ainsi qu'un spectre
juste avant ou juste après ce transit secondaire, ainsi qu'un spectre 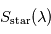 de l'étoile seule pendant ce transit secondaire, on peut en déduire le spectre
de l'étoile seule pendant ce transit secondaire, on peut en déduire le spectre 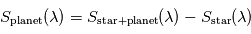 émis ou réfléchi par la planète seule vue à angle de phase nul.
émis ou réfléchi par la planète seule vue à angle de phase nul.
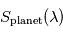 peut alors être analysé comme le serait n'importe quel spectre (par exemple en termes de température ou de composition pour un spectre thermique, ou bien de propriétés des diffuseurs pour un spectre réfléchi). C'est du moins le cas en théorie, car en pratique le faible rapport signal à bruit de tels spectres interdit à ce jour toute analyse trop poussée de ces spectres, de résolution spectrale souvent médiocre.
peut alors être analysé comme le serait n'importe quel spectre (par exemple en termes de température ou de composition pour un spectre thermique, ou bien de propriétés des diffuseurs pour un spectre réfléchi). C'est du moins le cas en théorie, car en pratique le faible rapport signal à bruit de tels spectres interdit à ce jour toute analyse trop poussée de ces spectres, de résolution spectrale souvent médiocre.

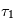 désigne l'épaisseur optique du milieu 1 ?
désigne l'épaisseur optique du milieu 1 ?
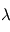 de la profondeur
de la profondeur 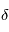 d'un transit primaire autour d'une étoile de rayon
d'un transit primaire autour d'une étoile de rayon 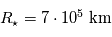 . Le meilleur ajustement par un modèle simple est représenté ci-dessous (l'axe des abscisses des gradué de façon logarithmique). L'échelle de hauteur de l'atmosphère de l'exoplanète sera supposée constante.
. Le meilleur ajustement par un modèle simple est représenté ci-dessous (l'axe des abscisses des gradué de façon logarithmique). L'échelle de hauteur de l'atmosphère de l'exoplanète sera supposée constante.

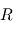 de la planète.
de la planète.
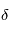 :
:
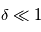
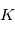 observée pour les courtes longueurs d'onde.
observée pour les courtes longueurs d'onde.
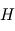 , puis la température sachant que l'on a aussi
, puis la température sachant que l'on a aussi 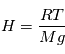 . On prendra
. On prendra 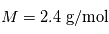 ,
, 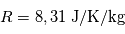 et
et 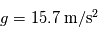 .
.
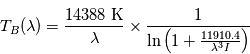 où la longueur d'onde
où la longueur d'onde 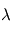 est en µm et la radiance
est en µm et la radiance 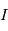 en
en 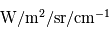


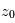 que l'on précisera.
que l'on précisera.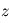 telles que :
telles que : 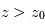 ,
, 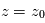 ,
, 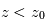 . Vérifiez la cohérence avec les variations de la densité de colonne d'ozone observées le long de ces rayons.
. Vérifiez la cohérence avec les variations de la densité de colonne d'ozone observées le long de ces rayons.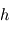 de la couche d'ozone.
de la couche d'ozone.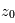 et
et 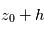 , montrer que la longueur
, montrer que la longueur 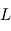 parcourue par le rayon d'altitude tangente
parcourue par le rayon d'altitude tangente 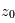 est donnée par
est donnée par 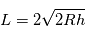 où
où 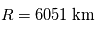 désigne le rayon de Vénus. On se placera dans l'hypothèse, vérifiée ici, où
désigne le rayon de Vénus. On se placera dans l'hypothèse, vérifiée ici, où 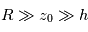 .
.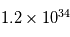 . Cette transmission théorique simplifiée ne prend en compte que l'ozone, et néglige l'absorption causée par le dioxyde de carbone.
. Cette transmission théorique simplifiée ne prend en compte que l'ozone, et néglige l'absorption causée par le dioxyde de carbone.
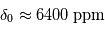 .
.
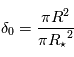 , d'où
, d'où 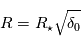 . L'application numérique donne
. L'application numérique donne 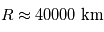 , soit une planète de taille intermédiaire entre Jupiter et Neptune.
, soit une planète de taille intermédiaire entre Jupiter et Neptune.
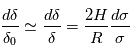 , d'où l'on tire
, d'où l'on tire 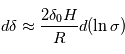 . La pente constante en
. La pente constante en 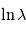 se traduit donc par
se traduit donc par 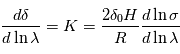 . Ceci n'est possible que si
. Ceci n'est possible que si 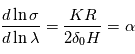 est constante, c'est-à-dire si
est constante, c'est-à-dire si 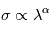 . Le phénomène le plus vraisembable est alors la diffusion Rayleigh causée par les molécules gazeuses. En ce cas,
. Le phénomène le plus vraisembable est alors la diffusion Rayleigh causée par les molécules gazeuses. En ce cas, 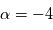 .
. 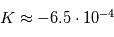 . Ne pas oublier que
. Ne pas oublier que 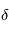 est en ppm ! (
est en ppm ! (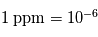 )
)
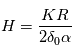 avec les notations précédentes, d'où
avec les notations précédentes, d'où 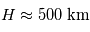 . Cela donne une température atmosphérique d'environ
. Cela donne une température atmosphérique d'environ 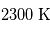 . Notons qu'une telle détermination est en pratique très imprécise, et donc d'intérêt limité.
. Notons qu'une telle détermination est en pratique très imprécise, et donc d'intérêt limité.