| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Lois du corps noir |
Nous allons à présent aborder les lois quantitatives permettant de modéliser simplement les profils verticaux de température au sein des atmosphères planétaires. Cela nécessite quelques rappels sur le rayonnement thermique, dit de "corps noir".
L'intensité lumineuse 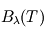 , définie comme la puissance émise par unité de surface émettrice, par angle solide autour de la direction du rayon et par unité de longueur d'onde
, définie comme la puissance émise par unité de surface émettrice, par angle solide autour de la direction du rayon et par unité de longueur d'onde 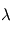 émise par tout corps noir idéal de température
émise par tout corps noir idéal de température 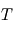 , est donnée par la loi de Planck :
, est donnée par la loi de Planck :
![\[ B_{\lambda}(T) = \frac{2 h c^2}{\lambda ^5} \frac{1}{\exp \left( \frac{hc}{\lambda kT} \right) -1} \]](../pages_fluide-temperature/equations_fluide-temperature-comprendre-noatm/equation4.png)
où 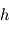 ,
, 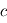 et
et 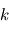 désignent respectivement les constantes fondamentales de Planck, de la vitesse de la lumière et de Maxwell-Boltzmann. Cette fonction possède des propriétés mathématiques aux conséquences importantes pour la suite du cours.
désignent respectivement les constantes fondamentales de Planck, de la vitesse de la lumière et de Maxwell-Boltzmann. Cette fonction possède des propriétés mathématiques aux conséquences importantes pour la suite du cours.
Elle donne la position du maximum en 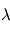 de
de 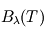 à température
à température 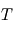 donnée, comme illustré précédemment.
donnée, comme illustré précédemment.
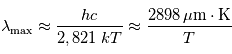
Autrement dit, plus le corps est chaud, et plus il émet principalement à des longueurs d'ondes courtes et ce de façon inversement proportionnelle. Cela justifie la séparation du spectre lumineux en :
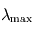 est voisin de
est voisin de 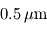 (soit dans le vert).
(soit dans le vert).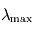 est voisin de
est voisin de 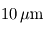 .
.
La séparation entre les deux domaines est prise de façon conventionnelle autour de 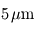 . Dans le contexte exoplanétaire, une remarque importante s'impose dès maintenant : la plupart des exoplanètes actuellement connues sont extrêmement chaudes, avec des températures excédant souvent
. Dans le contexte exoplanétaire, une remarque importante s'impose dès maintenant : la plupart des exoplanètes actuellement connues sont extrêmement chaudes, avec des températures excédant souvent 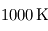 , si bien que la limite entre infrarouge thermique et lumière stellaire est décalée vers de plus courtes longueurs d'onde, voire devient complètement dénuée de sens. Cela empêche notamment d'appliquer tels quels les modèles atmosphériques conçus dans le système solaire qui distinguent ces deux catégories.
, si bien que la limite entre infrarouge thermique et lumière stellaire est décalée vers de plus courtes longueurs d'onde, voire devient complètement dénuée de sens. Cela empêche notamment d'appliquer tels quels les modèles atmosphériques conçus dans le système solaire qui distinguent ces deux catégories.
Lorsque l'on ne s'intéresse pas au détail du spectre émis par le corps noir, il est souvent intéressant de calculer le flux (c'est à dire la puissance par unité de surface émettrice) total émis par le corps noir dans un demi-espace (par exemple, pour une surface planétaire, vers le haut). Pour cela, il suffit d'intégrer la loi de Planck sur sa variable spectrale 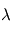 , et sur les
, et sur les 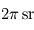 d'angle solide en question. Le calcul donne alors le résultat suivant, connu sous le nom de loi de Stefan-Boltzmann :
d'angle solide en question. Le calcul donne alors le résultat suivant, connu sous le nom de loi de Stefan-Boltzmann :
![\[ F = \sigma T^4 \]](../pages_fluide-temperature/equations_fluide-temperature-comprendre-noatm/equation20.png)
où 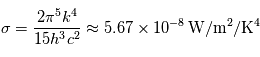 est connu sous le nom de constante de Stefan-Boltzmann. La puissance émise par un corps noir dépend donc énormément de sa température (une augmentation relative de
est connu sous le nom de constante de Stefan-Boltzmann. La puissance émise par un corps noir dépend donc énormément de sa température (une augmentation relative de 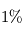 de sa température entraîne ainsi une augmentation d'environ
de sa température entraîne ainsi une augmentation d'environ 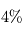 du flux émis).
du flux émis).