Caractéristiques des ondes

Auteurs: Thomas Navarro, Arianna Piccialli

Caractéristique d'une onde

Au bout d'une durée correspondant à une période

, l'onde aura aura la même allure.

Crédit : A. Piccialli

Les ondes atmosphériques sont des perturbations des champs atmosphériques qui se propagent dans l'espace et/ou le temps. C'est un mécanisme important dans la dynamique des atmosphères car les ondes permettent de transporter des perturbations, transporter de l'énergie et de la quantité de mouvement d'une région à une autre.

Propriétés des ondes

On peut représenter de manière simplifiée une onde atmosphérique par une fonction sinusoïdale, en fonction d'une dimension spatiale de coordonnée 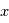et d'une dimension temporelle de coordonnée :

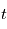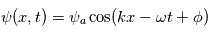
$\psi(x,t)=\psi_a\cos(k x-\omega t + \phi)$

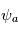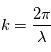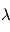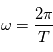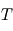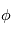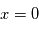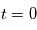Où $\psi_a$ est l'amplitude de l'onde; $k=\frac{2\pi}{\lambda}$ est le nombre d'onde; $\lambda$ est la longueur d'onde (en mètres); $\omega=\frac{2\pi}{T}$ est la pulsation; est la période (en secondes). $\phi$ est la phase de l'onde, c'est-à-dire la valeur de la perturbation lorsque x=0 et t=0 . La longueur d'onde est définie comme étant la distance séparant deux crêtes consécutives d'une onde. 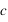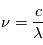Si (en mètres par seconde) est la vitesse de propagation de l'onde, on définit la fréquence (en hertz) par : $\nu=\frac{c}{\lambda}$ .

Le champ physique représenté par 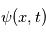$\psi(x,t)$ est une variable atmosphérique. Il peut s'agir de la température, pression, le vent, etc ... La dimension de l'amplitude 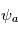$\psi_a$ est donc la même que celle de la variable représentée par la perturbation $\psi$ .

Notation exponentielle

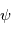Une manière plus compacte et efficace pour représenter une onde est la notation exponentielle. On écrit la perturbation sous sa forme complexe de la manière suivante :

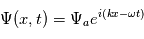
$\Psi(x,t)=\Psi_ae^{i(kx-\omega t)}$

Avec 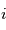le nombre imaginaire 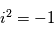i^2=-1 . La perturbation réelle est définie comme étant la partie réelle de sa forme complexe :

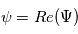
$\psi=Re(\Psi)$

En utilisant la relation trigonométrique bien connue 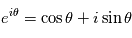$e^{i\theta}=\cos\theta +i\sin\theta$ , on obtient que l'amplitude complexe 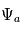$\Psi_a$ vaut :

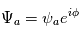
$\Psi_a=\psi_a e^{i\phi}$

L'amplitude complexe 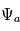$\Psi_a$ contient ainsi l'information à la fois sur l'amplitude 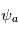$\psi_a$ et la phase 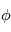$\phi$ de l'onde. Cette notation est très pratique car elle permet notamment de dériver ou d'intégrer une onde par rapport à l'espace ou au temps. Par exemple :

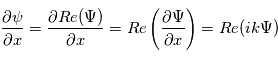
$\frac{\partial\psi}{\partial x} = \frac{\partial Re(\Psi)}{\partial x} = Re\left(\frac{\partial \Psi}{\partial x}\right) = Re(ik\Psi)$

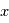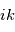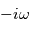Ainsi, dériver par rapport à la coordonnée spatiale revient à multiplier l'onde complexe par . De même, une dérivation temporelle revient à multiplier par $-i\omega$ .

De la même manière, on peut montrer que trouver une primitive de l'onde complexe revient à diviser par 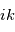, donc à multiplier par 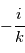$-\frac{i}{k}$ . De même, multiplier par 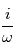$\frac{i}{\omega}$ permet de trouver une primitive par rapport à .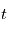