Onde sonore

Auteurs: Thomas Navarro, Arianna Piccialli

Méthode des perturbations

À partir des équations primitives, il est possible de trouver les ondes susceptibles de se propager dans l'atmopshère en utilisant la méthode des perturbations. Il s'agit d'écrire chaque champ (par exemple avec la pression 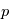) comme étant la somme d'une valeur fixe 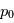p_0 solution des équations et d'une petite perturbation 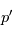: 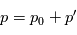p=p_0+p' . Ceci permet de linéariser les équations primitives en obtenant une équation pour les petites pertubations. Ces pertubations correspondent à des ondes que l'on peut ainsi étudier au moyen d'un cadre formel.

Onde sonore

L'onde la plus évidente est l'onde sonore dont le calcul va être détaillé ci-dessous. On définit les petites perturbations comme étant des ondes se propageant horizontalement et verticalement :

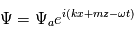
$\Psi = \Psi_a e^{i(kx+mz-\omega t)}$

avec 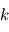et 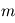les nombres d'ondes horizontaux et verticaux respectivement. On fait l'approximation que la rotation et la gravité sont négligeables dans le cas qui nous intéresse. De plus, on suppose un fluide au repos, où la dérivée lagrangienne est égale à la dérivée eulérienne. Ainsi dans les équations primitives la force de Coriolis s'annule, tout comme la force centrifuge. 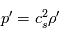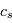En posant $p'=c_s^2\rho'$ avec c_s la vitesse du son, les équations du mouvement horizontal et de l'équation de continuité s'écrivent ainsi :

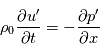
$\rho_0\frac{\partial u'}{\partial t} = - \frac{\partial p'}{\partial x}$

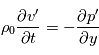
$\rho_0\frac{\partial v'}{\partial t} = - \frac{\partial p'}{\partial y}$

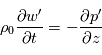
$\rho_0\frac{\partial w'}{\partial t} = - \frac{\partial p'}{\partial z}$

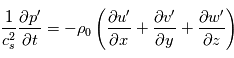
$\frac{1}{c_s^2}\frac{\partial p'}{\partial t} = - \rho_0\left( \frac{\partial u'}{\partial x} + \frac{\partial v'}{\partial y} +\frac{\partial w'}{\partial z} \right)$

Soit, en utilisant les propriétés de la notation exponentielle :

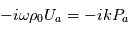
$-i\omega \rho_0 U_a = -ikP_a$

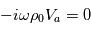
$-i\omega \rho_0 V_a = 0$

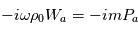
$-i\omega \rho_0 W_a = -imP_a$

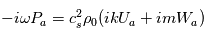
$-i\omega P_a= c_s^2\rho_0(ikU_a+imW_a)$

Par identification, on obtient :

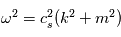
$\omega^2=c_s^2(k^2+m^2)$

qui nous donne la relation entre longueur d'onde et période d'une onde sonore.

Généralisation

Le traitement des ondes atmosphériques est un sujet complexe; dans la page qui suit, nous allons donner un aperçu général des principaux types d'ondes en comparant différentes planètes, mais sans entrer dans le détail.

Une analyse plus détaillée des phénomènes ondulatoires peut être trouvé dans la liste suivante des livres:

A. Sanchez-Lavega "An Introduction to Planetary atmospheres" CRC Press, Taylor & Francis Group, 2011.
J. Holton "An Introduction to Dynamic Meteorology" Elsevier Academic Press, 2004.