Nombre de Richardson

Auteurs: Thomas Navarro, Arianna Piccialli

Définition

Pour caractériser les différents types des instabilités atmosphériques on utilise le nombre de Richardson, un nombre sans dimension défini par:

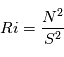
$Ri=\frac{N^2}{S^2}$

Où 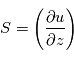$S=\left(\frac{\partial{u}}{\partial{z}}\right)$ est le cisaillement vertical du vent.

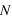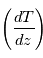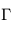est nommée fréquence de Brunt-Väisälä définie comme la différence entre le gradient vertical de température $\left(\frac{dT}{dz}\right)$ et le gradient adiabatique $\Gamma$ :

$N^2=\frac{g}{T}\left[\left(\frac{dT}{dz}\right)-\Gamma\right]$

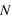est la fréquence d'oscillation d'une particule soumise à un déplacement vertical. Pour 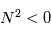N^2<0 l'atmosphère est instable et une particule déplacée de son état initial s'éloignera irréversiblement. Si 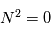N^2=0 , la stabilité est "neutre", la particule déplacée demeura à sa nouvelle altitude. Enfin, pour 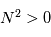N^2>0 se produit une oscillation de la particule autour de son état initial.

Interprétation

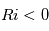: Instabilité verticale
Dans ce cas, correspondant à un valeur négative de la fréquence de Brunt-Väisälä 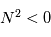, la couche atmosphérique est instable et la turbulence est soutenue par la convection.
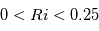: Instabilité de Kelvin-Helmholtz
Parfois on observe de la turbulence dans des couches atmosphèriques thermiquement stables. Cette turbulence, dite de Kelvin-Helmholtz, est crée dans des régions où il y a du cisaillement du vent. Un valeur positive de nombre de Richardson au-dessous d'une valeur critique 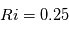est une condition nécessaire afin que l'instabilité de Kelvin-Helmholtz se puisse produire. L'écoulement de Kelvin-Helmholtz est le résultat du cisaillement de vitesse entre deux fluides glissant l'un par rapport à l'autre.
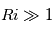$Ri\gg 1$ : Atmosphère stable
Condition suffisante pour une écoulement stable.