Les ondes atmosphériques sont des perturbations des champs atmosphériques qui se propagent dans l'espace et/ou le temps. C'est un mécanisme important dans la dynamique des atmosphères car les ondes permettent de transporter des perturbations, transporter de l'énergie et de la quantité de mouvement d'une région à une autre.
Onde sonore
L'onde la plus évidente est l'onde sonore dont le calcul va être détaillé ci-dessous. On définit les petites perturbations comme étant des ondes se propageant horizontalement et verticalement :
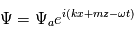
avec 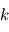 et
et 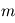 les nombres d'ondes horizontaux et verticaux respectivement. On fait l'approximation que la rotation et la gravité sont négligeables dans le cas qui nous intéresse. De plus, on suppose un fluide au repos, où la dérivée lagrangienne est égale à la dérivée eulérienne. Ainsi dans les équations primitives la force de Coriolis s'annule, tout comme la force centrifuge. En posant
les nombres d'ondes horizontaux et verticaux respectivement. On fait l'approximation que la rotation et la gravité sont négligeables dans le cas qui nous intéresse. De plus, on suppose un fluide au repos, où la dérivée lagrangienne est égale à la dérivée eulérienne. Ainsi dans les équations primitives la force de Coriolis s'annule, tout comme la force centrifuge. En posant 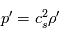 avec
avec 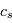 la vitesse du son, les équations du mouvement horizontal et de l'équation de continuité s'écrivent ainsi :
la vitesse du son, les équations du mouvement horizontal et de l'équation de continuité s'écrivent ainsi :
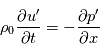
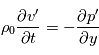
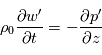
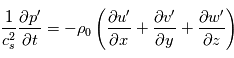
Soit, en utilisant les propriétés de la notation exponentielle :
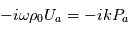
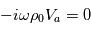
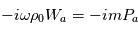
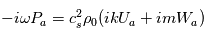
Par identification, on obtient :
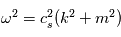
qui nous donne la relation entre longueur d'onde et période d'une onde sonore.
Généralisation
Le traitement des ondes atmosphériques est un sujet complexe; dans la page qui suit, nous allons donner un aperçu général des principaux types d'ondes en comparant différentes planètes, mais sans entrer dans le détail.
Une analyse plus détaillée des phénomènes ondulatoires peut être trouvé dans la liste suivante des livres:
- A. Sanchez-Lavega "An Introduction to Planetary atmospheres" CRC Press, Taylor & Francis Group, 2011.
- J. Holton "An Introduction to Dynamic Meteorology" Elsevier Academic Press, 2004.
Les ondes atmosphériques peuvent se manifester de diverses manières: comme oscillations de la température, de la densité et de la vitesse du vent, ou à travers des structures régulières de nuages. Ils peuvent être classés sur la base de facteurs différents: (1) mécanismes de restauration; (2) échelles de temps et d'espace; (3) ondes stationnaires ou qui se déplacent.
 Classement des ondes
Classement des ondes
- Ondes de gravité:
Le mécanisme de restauration des ondes de gravité est la poussée d'Archimède. Elles sont créées: (1) par la topographie (ondes orographiques), lors du passage d'une masse d'air au-dessus d'un relief montagneux; ou (2) par des instabilités dues à la présence d'orages ou de fronts d'air. Ils sont très communs dans les mésosphères des planètes telluriques. Sur Terre, les ondes de gravité révèlent souvent leur présence à travers des formations nuageuses, comme dans le cas des ondes orographiques. À des altitudes plus élevées, des images des nuages polaires mésosphériques, aussi connus sous le nom de nuages noctulescents, montrent souvent des structures ondulatoires probablement dues à la propagation vers le haut des ondes de gravité. Dans l'atmosphère martienne, des ondes de gravité ont été observées dans des images de nuages mésosphériques de glace de CO2 obtenues par la High Resolution Stereo Camera à bord de la mission européenne Mars Express et elles sont produites par la topographie (montagnes et cratères). Plusieurs missions spatiales ont détecté des ondes de gravité dans l'atmosphère de Vénus à la fois comme des oscillations sur le champ de température et comme des structures sur la couche de nuages. Elles sont probablement causées par des mouvements convectifs ou par des instabilité de de Kelvin-Helmholtz. Dans la haute atmosphère des planètes géantes (Jupiter, Uranus, et Neptune), des ondes de gravité ont été détectées par des oscillations dans les profils verticaux de température. Elles sont probablement la manifestation d'ondes de gravité générées près de la tropopause se propageant vers le haut.
- Ondes de Kelvin-Helmholtz:
Ces ondes sont un type d'ondes de gravité produites par l'instabilité de Kelvin-Helmholtz (Figure 2).
- Ondes de Rossby:
Les ondes de Rossby ou ondes planétaires sont caracterisées par une grande longueur d'onde. Elles sont dues à la variation de la force de Coriolis selon la latitude, quand une masse d'air se déplace à latitudes plus ou moins élevées. Sur la Terre, les ondes de Rossby sont des phénomènes permanents dans les latitudes moyennes et sous-polaires. Souvent, des cyclones et des anticyclones se forment dans les crêtes de l'onde. De la même façon, des ondes de Rossby se forment dans l'atmosphère vers les régions polaires de Mars. Dans les planètes géantes Jupiter et Saturne, il y a une grande variété d'ondes atmosphériques à l'extérieur de la région équatoriale qu'on suppose être des ondes de Rossby. Sur Saturne, un système ondulatoire hexagonal existe autour du pôle Nord, qui pourrait être une onde de Rossby. On peut voir divers exemples d'ondes de Rossby sur différentes planètes dans la figure ci-contre.
- Ondes de marées thermiques:
Les ondes de marées thermiques sont des ondes d'échelle planétaire excitées par les variations de l'insolation du sol dues au cycle jour-nuit. Ces ondes se manifestent sur le champ de pression et sur les composants du vent et elles évoluent avec le temps solaire local. Les ondes de marée thermique dans l'atmosphère de Mars ont une amplitude beaucoup plus élevée que sur la Terre car le forçage thermique sur Mars est très fort à cause de l'absorption dans le proche infra-rouge du 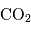 atmosphérique, l'absorption du rayonnement infra-rouge émis par la surface, la présence de la poussière dans l'atmosphère et le fait que l'atmosphère y soit plus ténue. L'effet des marées thermiques sur la circulation zonale et méridienne moyenne est donc très important dans l'atmosphère martienne. Sur Vénus, l'absorption du rayonnement solaire se produit essentiellement dans la couche de nuages et des études ont proposé que les marées solaires jouent un rôle important dans la super-rotation de Vénus à ce niveau.
atmosphérique, l'absorption du rayonnement infra-rouge émis par la surface, la présence de la poussière dans l'atmosphère et le fait que l'atmosphère y soit plus ténue. L'effet des marées thermiques sur la circulation zonale et méridienne moyenne est donc très important dans l'atmosphère martienne. Sur Vénus, l'absorption du rayonnement solaire se produit essentiellement dans la couche de nuages et des études ont proposé que les marées solaires jouent un rôle important dans la super-rotation de Vénus à ce niveau.
Figure 1

Crédit :
A. Piccialli
Figure 2

Ondes de Kelvin-Helmholtz observés au-dessus de Rome.
Crédit :
Angelo Zinzi
 Propriétés des ondes
Propriétés des ondes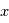 et d'une dimension temporelle de coordonnée
et d'une dimension temporelle de coordonnée 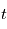 :
:
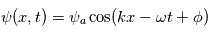
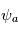 est l'amplitude de l'onde;
est l'amplitude de l'onde; 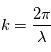 est le nombre d'onde;
est le nombre d'onde; 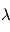 est la longueur d'onde (en mètres);
est la longueur d'onde (en mètres); 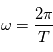 est la pulsation;
est la pulsation; 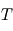 est la période (en secondes).
est la période (en secondes). 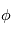 est la phase de l'onde, c'est-à-dire la valeur de la perturbation lorsque
est la phase de l'onde, c'est-à-dire la valeur de la perturbation lorsque 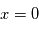 et
et 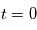 .
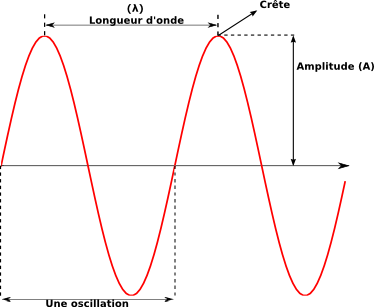
La longueur d'onde est définie comme étant la distance séparant deux crêtes consécutives d'une onde. Si
.
La longueur d'onde est définie comme étant la distance séparant deux crêtes consécutives d'une onde. Si 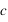 (en mètres par seconde) est la vitesse de propagation de l'onde, on définit la fréquence (en hertz) par :
(en mètres par seconde) est la vitesse de propagation de l'onde, on définit la fréquence (en hertz) par : 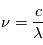 .
.
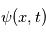 est une variable atmosphérique. Il peut s'agir de la température, pression, le vent, etc ... La dimension de l'amplitude
est une variable atmosphérique. Il peut s'agir de la température, pression, le vent, etc ... La dimension de l'amplitude 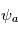 est donc la même que celle de la variable représentée par la perturbation
est donc la même que celle de la variable représentée par la perturbation 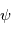 .
.
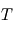 , l'onde aura aura la même allure.
, l'onde aura aura la même allure.
 Notation exponentielle
Notation exponentielle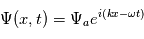
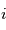 le nombre imaginaire
le nombre imaginaire 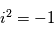 . La perturbation réelle est définie comme étant la partie réelle de sa forme complexe :
. La perturbation réelle est définie comme étant la partie réelle de sa forme complexe :
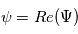
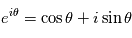 , on obtient que l'amplitude complexe
, on obtient que l'amplitude complexe 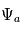 vaut :
vaut :
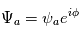
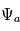 contient ainsi l'information à la fois sur l'amplitude
contient ainsi l'information à la fois sur l'amplitude 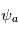 et la phase
et la phase 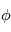 de l'onde. Cette notation est très pratique car elle permet notamment de dériver ou d'intégrer une onde par rapport à l'espace ou au temps. Par exemple :
de l'onde. Cette notation est très pratique car elle permet notamment de dériver ou d'intégrer une onde par rapport à l'espace ou au temps. Par exemple :
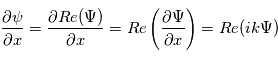
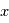 revient à multiplier l'onde complexe par
revient à multiplier l'onde complexe par 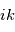 . De même, une dérivation temporelle revient à multiplier par
. De même, une dérivation temporelle revient à multiplier par 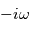 .
.
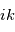 , donc à multiplier par
, donc à multiplier par 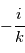 . De même, multiplier par
. De même, multiplier par 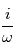 permet de trouver une primitive par rapport à
permet de trouver une primitive par rapport à 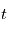 .
.
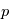 ) comme étant la somme d'une valeur fixe
) comme étant la somme d'une valeur fixe 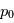 solution des équations et d'une petite perturbation
solution des équations et d'une petite perturbation 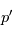 :
: 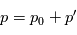 . Ceci permet de linéariser les équations primitives en obtenant une équation pour les petites pertubations. Ces pertubations correspondent à des ondes que l'on peut ainsi étudier au moyen d'un cadre formel.
. Ceci permet de linéariser les équations primitives en obtenant une équation pour les petites pertubations. Ces pertubations correspondent à des ondes que l'on peut ainsi étudier au moyen d'un cadre formel.
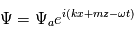
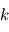 et
et 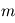 les nombres d'ondes horizontaux et verticaux respectivement. On fait l'approximation que la rotation et la gravité sont négligeables dans le cas qui nous intéresse. De plus, on suppose un fluide au repos, où la dérivée lagrangienne est égale à la dérivée eulérienne. Ainsi dans les
les nombres d'ondes horizontaux et verticaux respectivement. On fait l'approximation que la rotation et la gravité sont négligeables dans le cas qui nous intéresse. De plus, on suppose un fluide au repos, où la dérivée lagrangienne est égale à la dérivée eulérienne. Ainsi dans les 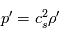 avec
avec 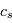 la vitesse du son, les équations du mouvement horizontal et de l'équation de continuité s'écrivent ainsi :
la vitesse du son, les équations du mouvement horizontal et de l'équation de continuité s'écrivent ainsi :
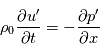
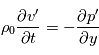
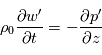
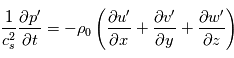
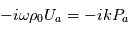
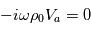
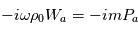
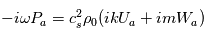
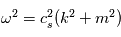
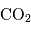 atmosphérique, l'absorption du rayonnement infra-rouge émis par la surface, la présence de la poussière dans l'atmosphère et le fait que l'atmosphère y soit plus ténue. L'effet des marées thermiques sur la circulation zonale et
atmosphérique, l'absorption du rayonnement infra-rouge émis par la surface, la présence de la poussière dans l'atmosphère et le fait que l'atmosphère y soit plus ténue. L'effet des marées thermiques sur la circulation zonale et 
