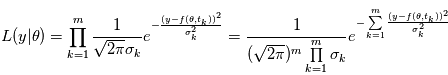| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
La vraisemblance |
Etant donné des paramètres 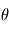 , le modèle global
, le modèle global 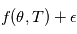 est une variable aléatoire: il est somme d'une variable aléatoire valant
est une variable aléatoire: il est somme d'une variable aléatoire valant 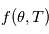 avec une probabilité 1 et d'un vecteur de variables aléatoires gaussienne
avec une probabilité 1 et d'un vecteur de variables aléatoires gaussienne 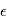 . A ce titre, il a une certaine densité de probabilité que l'on note
. A ce titre, il a une certaine densité de probabilité que l'on note 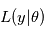 . Le symbole | se lisant "sachant". La lettre L vient de Likelihood, qui veut dire vraisemblance en anglais. Il s'agit dans l'idée de la probabilité d'obtenir
. Le symbole | se lisant "sachant". La lettre L vient de Likelihood, qui veut dire vraisemblance en anglais. Il s'agit dans l'idée de la probabilité d'obtenir 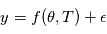 pour une valeur de
pour une valeur de 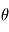 donnée..
donnée..
La fonction 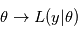 est souvent appelée "fonction de vraisemblance". La valeur de
est souvent appelée "fonction de vraisemblance". La valeur de 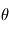 maximisant
maximisant 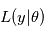 est appelé l'estimateur du maximum de vraisemblance. Il a de bonnes propritétés statistiques. En effet, on peut montrer que c'est un estimateur:
est appelé l'estimateur du maximum de vraisemblance. Il a de bonnes propritétés statistiques. En effet, on peut montrer que c'est un estimateur:
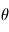
Dans notre cas, si les 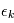 sont des variables indépendantes, leur densité de probabilité jointe est égale au produit de leurs densité de probabilité.
sont des variables indépendantes, leur densité de probabilité jointe est égale au produit de leurs densité de probabilité. 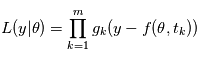 où
où 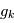 est la densité de probabilité de la variable
est la densité de probabilité de la variable 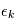 . De plus, si ces varibles sont gaussiennes et indépendantes, on a:
. De plus, si ces varibles sont gaussiennes et indépendantes, on a: