| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Exercices |
Difficulté : ☆☆☆
On rappelle que l'espérance et la variance d'une variable alétoire 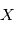 de densité de probabilité
de densité de probabilité  sont données par
sont données par 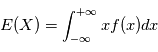 et
et 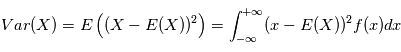
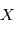 une variable aléatoire et
une variable aléatoire et 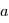 un réel. Montrer que
un réel. Montrer que 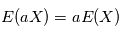 et
et 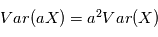
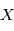 et
et 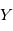 deux variables aléatoires indépendantes. Montrer que
deux variables aléatoires indépendantes. Montrer que 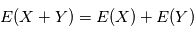 .
.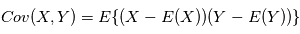 . Montrer que
. Montrer que 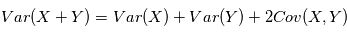
 mesures entachées de bruits gaussiens d'une quantité fixe
mesures entachées de bruits gaussiens d'une quantité fixe 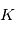 . Plus précisément, la mesure numéro
. Plus précisément, la mesure numéro 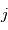 est modélisée par une variable aléatoire
est modélisée par une variable aléatoire 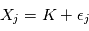 où
où  est un bruit gaussien de moyenne nulle et de variance
est un bruit gaussien de moyenne nulle et de variance  . On suppose que les mesures sont indépendantes, ce qui implique en particulier que
. On suppose que les mesures sont indépendantes, ce qui implique en particulier que 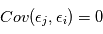 pour
pour 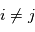 . Pour obtenir une estimation de
. Pour obtenir une estimation de 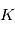 , on fait la moyenne empirique des expériences, c'est à dire
, on fait la moyenne empirique des expériences, c'est à dire 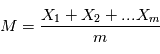 . Montrer que
. Montrer que 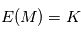 et
et 
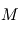 augmente-t-elle avec le nombre de mesures ?
augmente-t-elle avec le nombre de mesures ?