| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
|
Pour décrire l'état de polarisation de la lumière on va utiliser une notation introduite par Gabriel Stokes : le vecteur de Stokes. Celui-ci est composé de quatre éléments : I, Q, U et V.
Le paramètre I décrit l'intensité de la lumière. L'intensité totale est 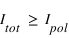 où
où 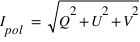 . Le degré de polarisation, décrivant la proportion de la lumière qui est polarisée est donc
. Le degré de polarisation, décrivant la proportion de la lumière qui est polarisée est donc 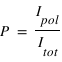 . Si on note
. Si on note 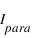 la polarisation parallèle au plan de référence et
la polarisation parallèle au plan de référence et 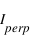 la composante polarisée perpendiculairement au plan de référence, on a
la composante polarisée perpendiculairement au plan de référence, on a 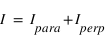 .
.
La polarisation linéaire est décrite par les éléments Q et U. Ils sont définis tels que (cf. figure):
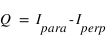
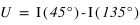
Le degré de polarisation linéaire se mesure alors avec 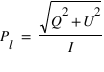 . Si on est dans le cas où
. Si on est dans le cas où 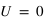 ,alors
,alors 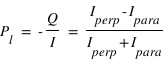 .
.
La polarisation circulaire se mesure avec V. Si V est positif, la polarisation est circulaire droite, si V est négatif, elle est gauche (du point de vue de la source, attention les conventions peuvent varier). Le degré de polarisation circulaire est alors simplement 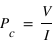 .
.