La polarisation est une propriété de la lumière. Cette dernière est une onde électromagnétique se déplaçant dans le vide à la vitesse c=299 792 458 m/s. Elle est composée d'un champ électrique (noté généralement E) et d'un champ magnétique (noté B), orthogonaux. À travers les équations de Maxwell, les champs E et B sont liés : la connaissance de l'un suffit pour connaitre l'autre. Aussi, pour simplifier — et c'est aussi la convention choisie en polarimétrie — on ne raisonne que sur le champ E.
Une onde électromagnétique plane se définit notamment par sa direction de propagation. Le plan perpendiculaire à la direction de propagation est appelé le plan d'onde. C'est dans le plan d'onde qu'évolue le champ E (et le champ B, mais nous n'en parlerons plus). À chaque instant, le champ E a une amplitude et une direction différente dans le plan d'onde. Dit autrement, si l'onde se propage en direction de l'observateur ce dernier verra le champ E former differents motifs dans le plan d'onde pendant son évolution temporelle. C'est cela qui va définir la polarisation de l'onde.
Une onde électromagnétique plane
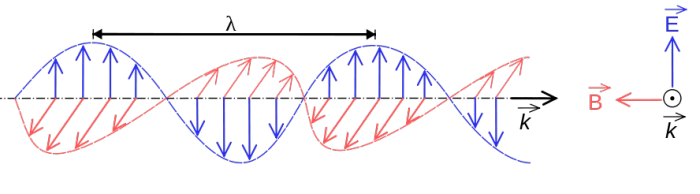
Schéma montrant une onde électromagnétique plane avec les champs E (en bleu) et B (en rouge) orthogonaux. Le vecteur k indique la direction de propagation. La longueur d'onde λ est indiquée également.
Crédit :
SuperManu, CC-BY-SA
Le cas le plus général est celui d'une polarisation elliptique, les autres situation pouvant être considérées comme des cas particuliers de celui-ci.
 Polarisation elliptique
Polarisation elliptique
Si le champ E dessine une ellipse dans le plan d'onde, on parle de polarisation elliptique.
C'est le cas le plus général. On peut alors décomposer le champ électrique selon deux composantes perpendiculaires :
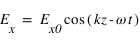
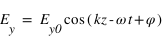 , où
, où 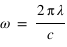 est la pulsation de l'onde électromagnétique;
est la pulsation de l'onde électromagnétique; 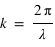 le nombre d'onde et φ le déphasage entre les deux composantes.
le nombre d'onde et φ le déphasage entre les deux composantes.
Champ E d'une onde polarisée elliptiquement.
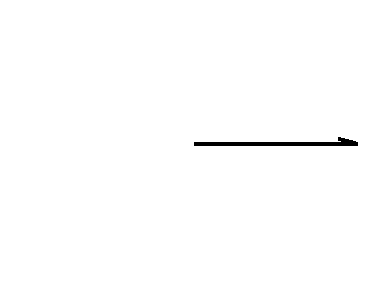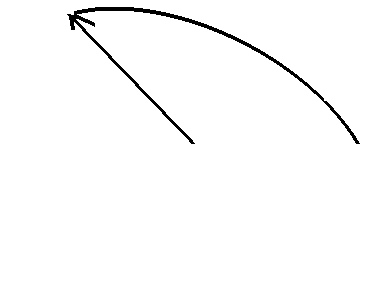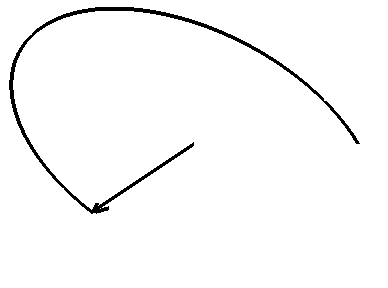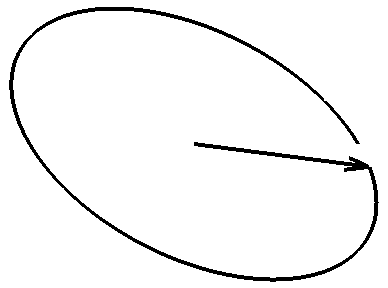
Vue du plan d'onde d'une onde électromagnétique polarisée elliptiquement. La direction de propagation « sort » de l'écran. (Cliquez sur l'image pour l'agrandir et voir l'animation)
Crédit :
Fffred
Polarisation elliptique

Onde polarisée elliptiquement. Les courbes bleue et rouge représentent les deux composantes orthogonales du champ électrique. Le champ E est indiqué en noir. La projection sur le plan d'onde (ligne jaune sur le plan bleu) donne une ellipse.
Crédit :
Inductiveload
Nous venons de voir la polarisation elliptique. On peut remarquer que si les deux axes principaux de l'ellipse sont égaux, l'ellipse devient un cercle : c'est la polarisation circulaire.
 Polarisation circulaire
Polarisation circulaire
Si le champ E dessine un cercle dans le plan d'onde, on parle de polarisation circulaire. Le sens de rotation de E définit une polarisation :
- Droite, si l'onde tourne dans le sens trigonométrique
- Gauche, si l'onde tourne dans le sens horaire
On peut se souvenir du sens de rotation en utilisant ses mains. En pointant son pouce vers soi, on regarde dans quel sens s'enroulent les autres doigts; en choisissant la main qui permet de reproduire le sens de rotation de l'onde polarisée (main gauche ou main droite), on détermine le sens de la polarisation !
On peut alors écrire les composantes du champ électrique comme suit :
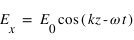
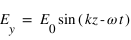 , où
, où 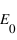 est l'amplitude commune des deux composantes du champ électrique. La phase vaut alors
est l'amplitude commune des deux composantes du champ électrique. La phase vaut alors 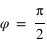 .
.
Champ E d'une onde polarisée circulairement.
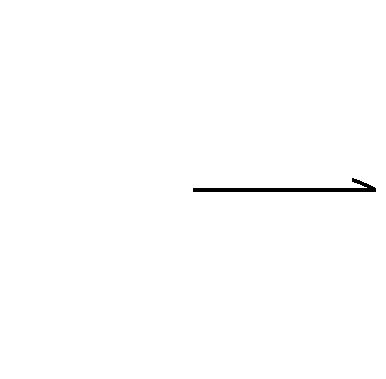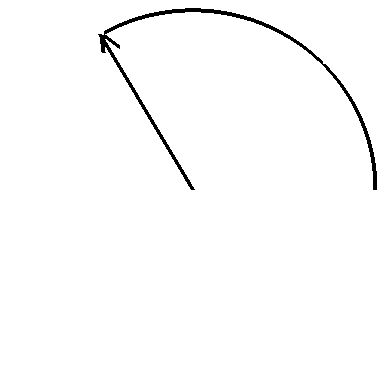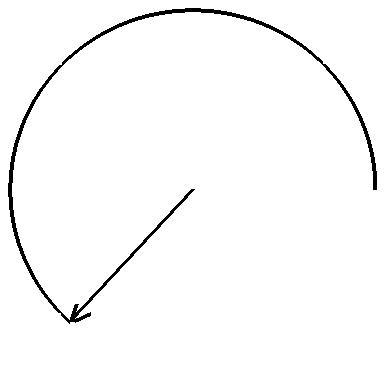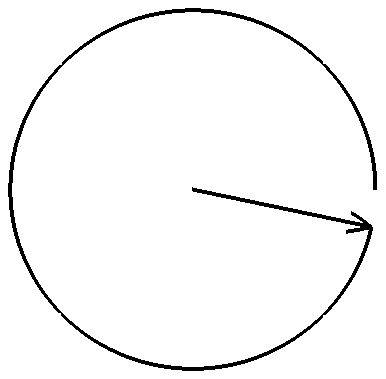
Vue du plan d'onde d'une onde électromagnétique polarisée circulairement. La direction de propagation « sort » de l'écran. Ici, la polarisation est droite vue depuis l'observateur. (Cliquer sur l'image pour l'agrandir et voir l'anumation)
Crédit :
Fffred
Polarisation circulaire

Onde polarisée circulairement. Les courbes bleue et rouge représentent les deux composantes orthogonales du champ électrique. Le champ E est indiqué en noir. La projection sur le plan d'onde (en noir sur le plan bleu) donne un cercle.
Crédit :
Inductiveload
 Attention aux conventions !
Attention aux conventions !
Attention ! Ceci est vrai si on se place du point de vue de l'observateur. Les directions doivent être interverties si on se place du point de vue de la source. Quand vous traitez des problèmes de polarisation, vérifiez toujours quelle est la convention utilisée.
 Polarisation linéaire
Polarisation linéaire
Si le champ E décrit un segment dans le plan d'onde, on dit que la polarisation est linéaire. On peut la voir comme une polarisation elliptique pour laquelle l'un des deux axes de l'ellipse de polarisation serait réduit à un point.
Le champ électrique s'écrit alors
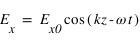
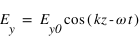 , avec
, avec 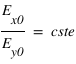 et
et 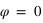 .
.
Le champ E d'une onde polarisée linéairement.

Vue du plan d'onde d'une onde électromagnétique polarisée linéairement. La direction de propagation « sort » de l'écran. (Cliquer sur l'image pour l'agrandir et voir l'animation)
Crédit :
Fffred
Polarisation linéaire

Onde polarisée linéairement. Les courbes bleue et rouge représentent les deux composantes orthogonales du champ électrique. Le champ E est indiqué en noir. La projection sur le plan d'onde (ligne jaune sur le plan bleu) donne une droite.
Crédit :
Inductiveload
Lumière non polarisée
On a abordé ici les types de polarisation, mais la lumière n'est pas forcément polarisée. Ou plutôt, un faisceau de lumière n'est pas polarisée d'une seule façon. On peut avoir une superposition de différentes polarisations linéaires, elliptiques et circulaires. La lumière naturelle est ainsi composée de multiples états de polarisation différents, donnant en moyenne une lumière non polarisée.
Pour les situations de polarisation linéaire, on décompose généralement la polarisation en deux composantes : la composante parallèle au plan de diffusion, et la composante qui lui est orthogonale. On représente souvent la lumière naturelle par un faisceau de lumière polarisée dans deux directions orthogonales. Un polariseur pourra alors filtrer l'une des composantes.
Lumière naturelle
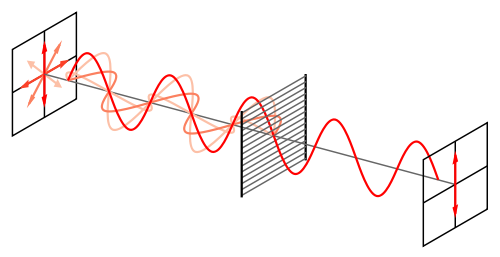
Exemple de lumière non polarisée venant de la gauche et traversant un filtre polarisant. Seule la composante polarisée linéairement et verticale est transmise.
Crédit :
Fffred CC-BY-SA
Sources non polarisées
Les sources naturellement polarisées ne sont pas communes. La lumière solaire est un bon exemple de lumière non polarisée. De même, le rayonnement thermique n'est généralement pas polarisé. Cependant, bien que les sources ne soient pas polarisées, la réflexion et la traversée de certains milieux peuvent modifier la polarisation de la lumière.
Un polariseur est un dispositif qui agit sur un faisceau de lumière incidente selon la polarisation de celui-ci. Il peut filtrer la lumière en ne laissant passer que certaines composantes de polarisation. Il peut aussi changer la polarisation d'un faisceau incident.
Les filtres polarisants
La plupart des polariseurs sont de simples filtres (la marque Polaroid en est un exemple connu), qui ne laisse passer la lumière polarisée que dans une direction particulière (on parle de direction ou d'axe du polariseur). Ainsi une lumière non-polarisée sera polarisée après avoir traversé un tel filtre. Une lumière polarisée ne sera totalement transmise que si la direction de polarisation incidente est la même que celle du filtre.
L'intensité transmise par un polariseur dépend des orientations du filtre et de l'onde incidente. Si on note 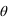 l'angle entre la direction du filtre et la direction de polarisation de l'onde incidente et
l'angle entre la direction du filtre et la direction de polarisation de l'onde incidente et 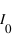 son intensité, on a après le polariseur une intensité
son intensité, on a après le polariseur une intensité 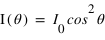 , c'est la Loi de Malus. De fait, on retrouve qu'un polariseur dont la direction de polarisation est perpendiculaire à celle de la lumière incidente, il ne transmettra rien. De même, deux polariseurs de directions perpendiculaires (on dit qu'ils sont croisés) ne laissent pas passer la lumière: celle-ci est polarisée dans une direction par le premier polariseur, puis bloquée par le second, de direction perpendiculaire. Dans le cas d'une source non polarisée
, c'est la Loi de Malus. De fait, on retrouve qu'un polariseur dont la direction de polarisation est perpendiculaire à celle de la lumière incidente, il ne transmettra rien. De même, deux polariseurs de directions perpendiculaires (on dit qu'ils sont croisés) ne laissent pas passer la lumière: celle-ci est polarisée dans une direction par le premier polariseur, puis bloquée par le second, de direction perpendiculaire. Dans le cas d'une source non polarisée 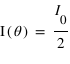 .
.
Illustration de la loi de Malus

Un polariseur (parfois appelé analyseur) devant une source polarisée linéairement . Selon l'angle que fait la direction du polariseur avec la polarisation de la lumière, le filtre laisse passer plus ou moins de lumière, conformément à la loi de Malus.
Crédit :
Rogilbert
Lames à retard
D'autres dispositifs optiques permettent de modifier la polarisation de la lumière. Les lames à retard sont utilisées à cet effet. On l'a vu précédemment, un faisceau polarisé peut être considéré comme étant la somme de deux composantes de polarisation orthogonales. Lors de la traversée d'une lame à retard, les propriétés de biréfringence de la lame vont faire qu'une des deux composantes est retardée par rapport à l'autre, ce qui va changer la polarisation en sortie. On dira que la lame a deux axes, un axe lent et un axe rapide.
Dans le cas d'une lame demi-onde, le déphasage entre les deux composantes est π (ou d'une demi-longueur d'onde, d'où son nom). De fait, si l'onde polarisée linéairement selon une direction faisant un angle θ avec l'axe rapide de la lame, elle ressortira avec une direction tournée d'un angle 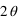 . L'utilisation principale qui en est faite est de changer la direction de polarisation linéaire. Une onde polarisée avec un angle
. L'utilisation principale qui en est faite est de changer la direction de polarisation linéaire. Une onde polarisée avec un angle 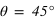 par rapport à l'axe rapide aura en sortie un angle
par rapport à l'axe rapide aura en sortie un angle 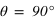 avec l'axe rapide : les directions incidentes et émergentes sont donc croisées !
avec l'axe rapide : les directions incidentes et émergentes sont donc croisées !
Lame à retard
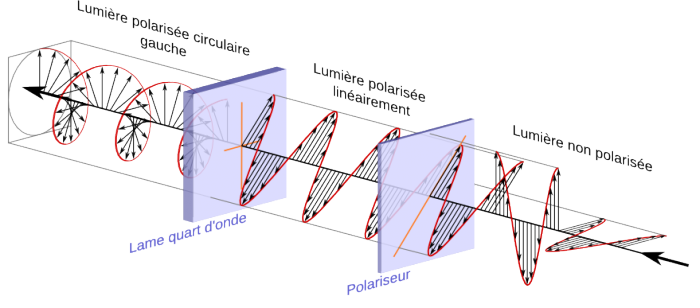
De la lumière non polarisée passe dans un polariseur qui la polarise linéairement avant de passer à travers une lame quart d'onde qui la transforme en lumière polarisée circulaire gauche.
Crédit :
Dave3457, domaine public, traduction Loïc Rossi
Dans le cas d'une lame quart d'onde, le déphasage vaut 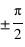 (ou un quart de longueur d'onde). Une telle lame permet de transformer une polarisation linéaire en une polarisation elliptique ou circulaire, et inversement. En effet dans le cas linéaire, les deux composantes du champ électrique, parallèle et perpendiculaire à l'axe rapide sont de la forme
(ou un quart de longueur d'onde). Une telle lame permet de transformer une polarisation linéaire en une polarisation elliptique ou circulaire, et inversement. En effet dans le cas linéaire, les deux composantes du champ électrique, parallèle et perpendiculaire à l'axe rapide sont de la forme 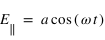 et
et 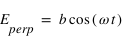 . Si on introduit un déphasage de
. Si on introduit un déphasage de 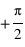 , les deux composantes deviendont
, les deux composantes deviendont 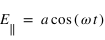 et
et 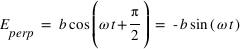 , le vecteur du champ électrique va donc décrire une ellipse !
, le vecteur du champ électrique va donc décrire une ellipse !
Attention ! Le fonctionnement des lames à retard dépend de la longueur d'onde !
Pour décrire l'état de polarisation de la lumière on va utiliser une notation introduite par Gabriel Stokes : le vecteur de Stokes. Celui-ci est composé de quatre éléments : I, Q, U et V.
Les éléments de Stokes
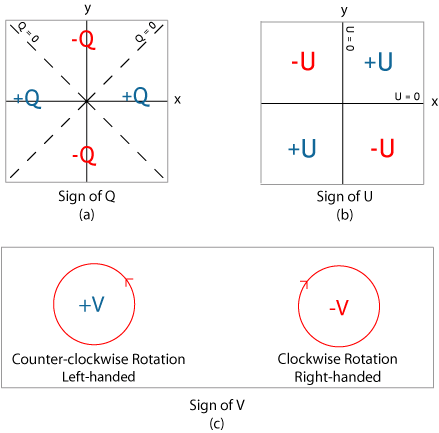
Figure illustrant les différents paramètres de Stokes.
Crédit :
Dan Moulton, CC-BY-SA
Polarisation linéaire
La polarisation linéaire est décrite par les éléments Q et U. Ils sont définis tels que (cf. figure):
Le degré de polarisation linéaire se mesure alors avec 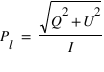 . Si on est dans le cas où
. Si on est dans le cas où 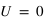 ,alors
,alors 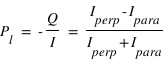 .
.
Polarisation circulaire
La polarisation circulaire se mesure avec V. Si V est positif, la polarisation est circulaire droite, si V est négatif, elle est gauche (du point de vue de la source, attention les conventions peuvent varier). Le degré de polarisation circulaire est alors simplement 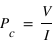 .
.

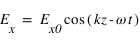
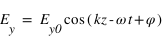 , où
, où 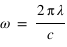 est la pulsation de l'onde électromagnétique;
est la pulsation de l'onde électromagnétique; 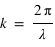 le nombre d'onde et
le nombre d'onde et 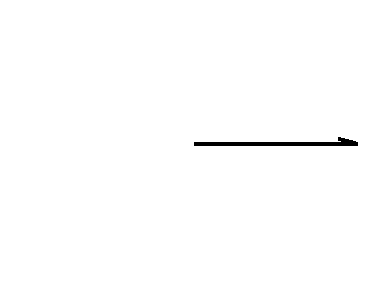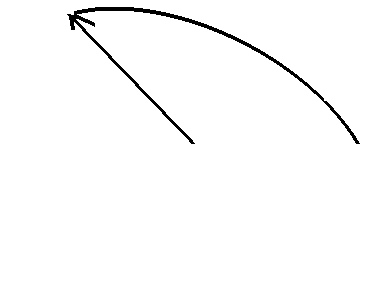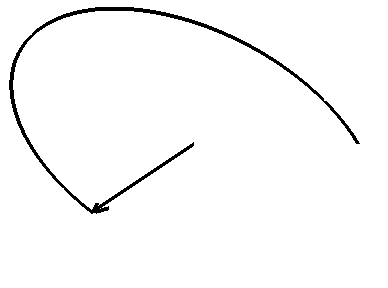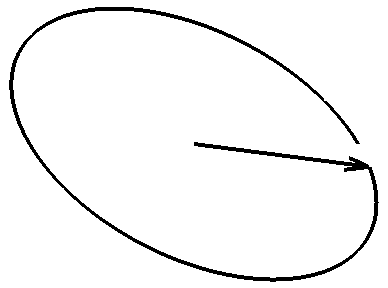

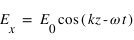
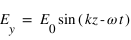 , où
, où 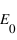 est l'amplitude commune des deux composantes du champ électrique. La phase vaut alors
est l'amplitude commune des deux composantes du champ électrique. La phase vaut alors 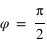 .
.


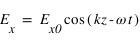
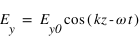 , avec
, avec 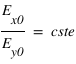 et
et 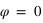 .
.



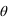 l'angle entre la direction du filtre et la direction de polarisation de l'onde incidente et
l'angle entre la direction du filtre et la direction de polarisation de l'onde incidente et 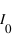 son intensité, on a après le polariseur une intensité
son intensité, on a après le polariseur une intensité 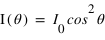 , c'est la Loi de Malus. De fait, on retrouve qu'un polariseur dont la direction de polarisation est perpendiculaire à celle de la lumière incidente, il ne transmettra rien. De même, deux polariseurs de directions perpendiculaires (on dit qu'ils sont croisés) ne laissent pas passer la lumière: celle-ci est polarisée dans une direction par le premier polariseur, puis bloquée par le second, de direction perpendiculaire. Dans le cas d'une source non polarisée
, c'est la Loi de Malus. De fait, on retrouve qu'un polariseur dont la direction de polarisation est perpendiculaire à celle de la lumière incidente, il ne transmettra rien. De même, deux polariseurs de directions perpendiculaires (on dit qu'ils sont croisés) ne laissent pas passer la lumière: celle-ci est polarisée dans une direction par le premier polariseur, puis bloquée par le second, de direction perpendiculaire. Dans le cas d'une source non polarisée 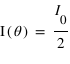 .
.

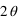 . L'utilisation principale qui en est faite est de changer la direction de polarisation linéaire. Une onde polarisée avec un angle
. L'utilisation principale qui en est faite est de changer la direction de polarisation linéaire. Une onde polarisée avec un angle 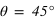 par rapport à l'axe rapide aura en sortie un angle
par rapport à l'axe rapide aura en sortie un angle 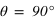 avec l'axe rapide : les directions incidentes et émergentes sont donc croisées !
avec l'axe rapide : les directions incidentes et émergentes sont donc croisées !

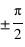 (ou un quart de longueur d'onde). Une telle lame permet de transformer une polarisation linéaire en une polarisation elliptique ou circulaire, et inversement. En effet dans le cas linéaire, les deux composantes du champ électrique, parallèle et perpendiculaire à l'axe rapide sont de la forme
(ou un quart de longueur d'onde). Une telle lame permet de transformer une polarisation linéaire en une polarisation elliptique ou circulaire, et inversement. En effet dans le cas linéaire, les deux composantes du champ électrique, parallèle et perpendiculaire à l'axe rapide sont de la forme 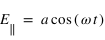 et
et 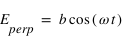 . Si on introduit un déphasage de
. Si on introduit un déphasage de 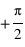 , les deux composantes deviendont
, les deux composantes deviendont 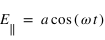 et
et 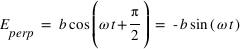 , le vecteur du champ électrique va donc décrire une ellipse !
, le vecteur du champ électrique va donc décrire une ellipse !

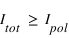 où
où 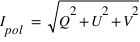 . Le degré de polarisation, décrivant la proportion de la lumière qui est polarisée est donc
. Le degré de polarisation, décrivant la proportion de la lumière qui est polarisée est donc 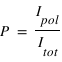 . Si on note
. Si on note 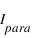 la polarisation parallèle au plan de référence et
la polarisation parallèle au plan de référence et 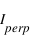 la composante polarisée perpendiculairement au plan de référence, on a
la composante polarisée perpendiculairement au plan de référence, on a 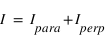 .
.
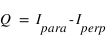
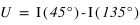
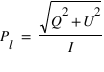 . Si on est dans le cas où
. Si on est dans le cas où 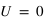 ,alors
,alors 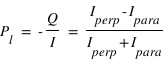 .
.
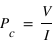 .
.