Polariseurs

Les filtres polarisants

La plupart des polariseurs sont de simples filtres (la marque Polaroid en est un exemple connu), qui ne laisse passer la lumière polarisée que dans une direction particulière (on parle de direction ou d'axe du polariseur). Ainsi une lumière non-polarisée sera polarisée après avoir traversé un tel filtre. Une lumière polarisée ne sera totalement transmise que si la direction de polarisation incidente est la même que celle du filtre.

L'intensité transmise par un polariseur dépend des orientations du filtre et de l'onde incidente. Si on note 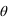l'angle entre la direction du filtre et la direction de polarisation de l'onde incidente et 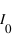son intensité, on a après le polariseur une intensité 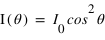, c'est la Loi de Malus. De fait, on retrouve qu'un polariseur dont la direction de polarisation est perpendiculaire à celle de la lumière incidente, il ne transmettra rien. De même, deux polariseurs de directions perpendiculaires (on dit qu'ils sont croisés) ne laissent pas passer la lumière: celle-ci est polarisée dans une direction par le premier polariseur, puis bloquée par le second, de direction perpendiculaire. Dans le cas d'une source non polarisée .

Lames à retard

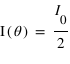D'autres dispositifs optiques permettent de modifier la polarisation de la lumière. Les lames à retard sont utilisées à cet effet. On l'a vu précédemment, un faisceau polarisé peut être considéré comme étant la somme de deux composantes de polarisation orthogonales. Lors de la traversée d'une lame à retard, les propriétés de biréfringence de la lame vont faire qu'une des deux composantes est retardée par rapport à l'autre, ce qui va changer la polarisation en sortie. On dira que la lame a deux axes, un axe lent et un axe rapide.

Dans le cas d'une lame demi-onde, le déphasage entre les deux composantes est π (ou d'une demi-longueur d'onde, d'où son nom). De fait, si l'onde polarisée linéairement selon une direction faisant un angle θ avec l'axe rapide de la lame, elle ressortira avec une direction tournée d'un angle 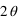. L'utilisation principale qui en est faite est de changer la direction de polarisation linéaire. Une onde polarisée avec un angle 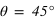par rapport à l'axe rapide aura en sortie un angle 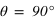avec l'axe rapide : les directions incidentes et émergentes sont donc croisées !

Lame à retard

De la lumière non polarisée passe dans un polariseur qui la polarise linéairement avant de passer à travers une lame quart d'onde qui la transforme en lumière polarisée circulaire gauche.

Crédit : Dave3457, domaine public, traduction Loïc Rossi

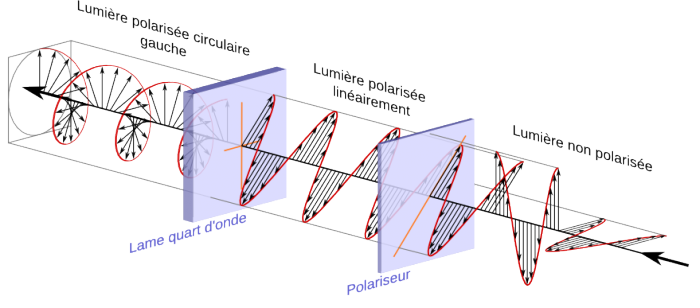
Dans le cas d'une lame quart d'onde, le déphasage vaut 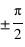(ou un quart de longueur d'onde). Une telle lame permet de transformer une polarisation linéaire en une polarisation elliptique ou circulaire, et inversement. En effet dans le cas linéaire, les deux composantes du champ électrique, parallèle et perpendiculaire à l'axe rapide sont de la forme 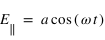et 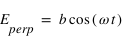. Si on introduit un déphasage de 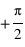, les deux composantes deviendon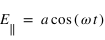t et 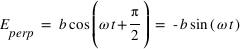, le vecteur du champ électrique va donc décrire une ellipse !

Attention ! Le fonctionnement des lames à retard dépend de la longueur d'onde !