Le filtrage et les lois de commande sont présentés car ce spaont des aspects essentiels d'un SCAO. Néanmoins, ce cours a simplement pour ambition de vous en faire une brève introduction.
En mathématiques et en ingénierie, la théorie du contrôle a comme objet l’étude du comportement de systèmes dynamiques. En électronique et traitement du signal, un filtre est originellement un circuit qui rejette une partie indésirable d'un signal. On appelle également filtre un outil logiciel dont le but est la séparation des fréquences contenues dans un signal numérisé.
L'estimation d'attitude consiste à estimer l'état actuel de l'orientation d'un satellite à partir d'un jeu d'observations et de références obtenues à partir de modèles. Ces observations ont été préalablement effectuées par des capteurs fixés sur le satellite. L'objectif est ici de trouver la meilleure estimation de l'état réel du système sous forme de matrice de changement de repère ou de quaternion d'attitude. La résolution exacte du problème n'est généralement pas possible car les observations sont entachées d'erreurs (erreurs de mesure, d'orientation du capteur, de modélisation...). De plus, on dispose souvent d'une surabondance d'information puisque plusieurs capteurs fournissent des informations par rapport à des références différentes (Soleil, champ magnétique, étoile...). On cherche alors à exploiter de manière optimale ces sources d'information en leur associant des modèles d'erreur.
Les problèmes de détermination d'attitude font intervenir des observations (orientation d'objets) pris à certaines dates. La détermination d'attitude statique représente le cas le plus simple, dans lequel on considère que toutes les mesures sont effectuées au même instant. Au contraire, lorsque le temps est introduit, on parle de détermination d'attitude récursive.
La qualité de la connaissance d'attitude dépend des limitations des capteurs, de la quantification des données, du temps d'échantillonnage et du traitement numérique. La détermination d'attitude embarquée est limitée par les capacités de filtrage de l'ordinateur de bord. Il arrive que pour obtenir une meilleure connaissance de l'attitude a posteriori les données des capteurs soient transmises au segment sol où elles sont post-traitées puis exploitables (par le segment sol ou le satellite).
Boucle SCA
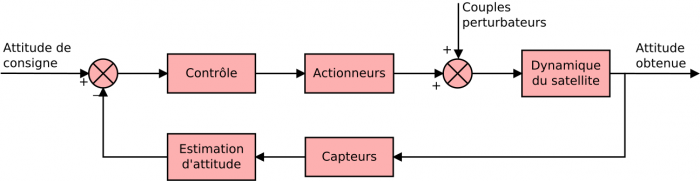
Boucle de contrôle d'attitude.
Crédit :
Gary Quinsac
Le cas particulier de l'estimation d'attitude à partir de mesures simultanées de directions non parallèles est ici introduit. À chaque observation sont associés deux vecteurs. Le premier est un vecteur unitaire 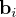 définissant la direction mesurée (observée) de la source (la Terre, le Soleil, une étoile, le champ magnétique terrestre...), exprimée dans le repère lié au satellite. Le second est un vecteur unitaire
définissant la direction mesurée (observée) de la source (la Terre, le Soleil, une étoile, le champ magnétique terrestre...), exprimée dans le repère lié au satellite. Le second est un vecteur unitaire 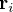 qui définit la direction de référence de la source, exprimée dans le repère origine (généralement inertiel). L'estimation d'attitude consiste ici à déterminer la matrice de transformation orthogonale
qui définit la direction de référence de la source, exprimée dans le repère origine (généralement inertiel). L'estimation d'attitude consiste ici à déterminer la matrice de transformation orthogonale  satisfaisant pour chaque observation i :
satisfaisant pour chaque observation i :
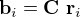
Méthode TRIAD
La méthode TRIAD se base sur l'observation de deux directions non-parallèles. Il s'agit de déterminer la MCD  permettant de transformer les vecteurs de référence
permettant de transformer les vecteurs de référence 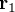 et
et 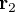 en vecteurs d'observation
en vecteurs d'observation 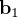 et
et 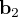 . Puisque l'on cherche à obtenir l'attitude suivant 3 axes, il nous faut créer deux bases orthonormées (y1, y2, y3) et (x1, x2, x3), respectivement associées aux vecteurs d'oservation et de référence. Il ne reste plus qu'à déduire la matrice de transformation orthogonale (ou MCD)
. Puisque l'on cherche à obtenir l'attitude suivant 3 axes, il nous faut créer deux bases orthonormées (y1, y2, y3) et (x1, x2, x3), respectivement associées aux vecteurs d'oservation et de référence. Il ne reste plus qu'à déduire la matrice de transformation orthogonale (ou MCD) 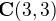 satisfaisant :
satisfaisant :
![\bold y_i = [C] \ \bold x_i](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation11.png) ,
, 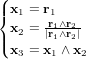 ,
, 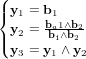
Cette méthode présente l'avantage d'être extrêmement simple, d'où son utilisation dans de nombreuses missions passées. De nos jours, cette méthode n'est plus considérée comme suffisamment précise. En effet, les mesures d'observation sont entachées d'erreur, ce qui empêche d'obtenir le même résultat suivant le vecteur d'observation choisi au départ. C'est pour cette raison que l'on choisit généralement l'observation la plus précise. Des techniques de calcul de la covarience de l'erreur de l'estimation ont été développées pour parer à ces inconvénients.
Méthode QUEST
Un critère quadratique peut être utilisé pour déterminer la matrice d'attitude. Cela revient à chercher la matrice orthogonale 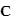 minimisant la fonction de moindres carrés :
minimisant la fonction de moindres carrés :
![L = \frac{1}{2} \ \sum_{i=1}^{n}{a_i \left| \bold b_i - [C] \bold r_i \right|^2}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation15.png)
La minimisation de ce critère n'a rien d'évident et de nombreuses méthodes ont été proposées. Il s'agit d'identifier les 9 paramètres de la MCD respectant les différentes contraintes énoncées précédemment (moindres carrés et règles de la MCD). L'algorithme QUEST (QUaternion ESTimation) offre une alternative intéressante. La forme quadratique est alors utilisée à la place de la MCD, permettant de réduire le nombre de paramètres. Nous ne rentrerons pas dans le détail de cette méthode dans le cadre de ce cours.
Dans le cas général où nous ne disposons pas de plusieurs mesures de directions non parallèles effectuées au même instant, le problème d'estimation devient dépendant du temps. Bien que des méthodes récursives basées sur l'algorithme QUEST aient été développées et utilisées, le filtrage de Kalman est le moyen le plus utilisé pour estimer l'attitude d'un satellite en présence de bruits de mesure.
Filtre de Kalman
Le filtre de Kalman a été développé en 1960 comme une nouvelle approche pour le filtrage linéaire et les problèmes de prédiction. Il permet de maintenir une estimation de l'état d'un système dynamique en dehors des périodes d'observation, à partir d'un modèle de son erreur. Puisqu'il s'agit d'un filtre récursif, la quantité d'informations à traiter reste limitée, ce qui en fait un filtre très apprécié à bord des satellites. On a pour habitude de distinguer deux phases dans ce type de filtres, la prédiction et la mise à jour :
- la phase de prédiction intervient lorsqu'aucune observation n'est disponible ; le filtre se base sur le modèle dynamique embarqué pour mettre à jour les paramètres estimés, tout en mettant à jour la matrice de covariance de l'erreur d'estimation ; cette dernière augmente durant cette phase en raison de l'incertitude inhérente au modèle dynamique,
- la mise à jour intervient lorsqu'une observation est disponible ; il devient alors possible de comparer la prédiction à l'observation ; les prédictions sont ainsi mises à jour, en tenant compte des incertitudes liées à l'observation et à la prédiction. Si les incertitudes liées aux observations sont plus faibles que celle du modèle alors cette phase fait décroître la covariance.
 Filtre de Kalman discret
Filtre de Kalman discret
C'est la version la plus simple du filtre de Kalman, seules l'estimation de l'état précédent et les mesures actuelles sont nécessaires.
Phase de prédiction
Durant la phase de prédiction, l'état et l'estimation de la covariance sont projetés dans le temps de l'état k-1 à l'état k :
![[Q]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation29.png) est la matrice de covariance du bruit de processus
est la matrice de covariance du bruit de processus 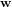 ,
, ![[P]_{k|k-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation31.png) est la matrice d'estimation a priori de la covariance de l'erreur.
est la matrice d'estimation a priori de la covariance de l'erreur.
À chaque étape le processus est répété afin d'obtenir de nouvelles estimations a posteriori à partir des estimations a priori. En pratique, la matrice de covariance ![[R]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation42.png) du bruit de mesure est déterminée avant d'utiliser le filtre et peut être mise à jour par la suite. Il est plus compliqué de déterminer la matrice de covariance du bruit de processus
du bruit de mesure est déterminée avant d'utiliser le filtre et peut être mise à jour par la suite. Il est plus compliqué de déterminer la matrice de covariance du bruit de processus ![[Q]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation43.png) car nous ne pouvons généralement pas directement observer le processus à estimer. Afin d'améliorer les performances du filtre, il est habituel de régler ces deux paramètres.
car nous ne pouvons généralement pas directement observer le processus à estimer. Afin d'améliorer les performances du filtre, il est habituel de régler ces deux paramètres.
La plupart des systèmes physiques, et notamment ceux étudiés, sont non linéaires. Le filtre de Kalman classique n'est donc optimal que sur une faible portion des phénomènes pris en compte. Dans le cas de systèmes non-linéaires, nous utilisons donc un filtre de Kalman étendu, ou "Extended Kalman Filter".
La théorie du contrôle s'intéresse au comportement de systèmes dynamiques en fonction de leurs paramètres. Elle peut être vue comme une stratégie permettant de sélectionner la bonne entrée d'un système pour que le sortie soit celle désirée. Cela fait partie du domaine de l'automatique.
Boucles ouvertes et fermées
Un système de contrôle est un mécanisme altérant l'état futur d'un système. En l'absence de retour d'information concernant la sortie du système, on se trouve dans le cas d'une boucle ouverte. Prenons l'exemple d'un lave-vaisselle. Celui-ci est programmé pour tourner un certain temps, à une certaine température et avec une certaine quantité d'eau. Ces paramètres ne dépendent pas de l'état de la vaisselle qu'il contient.
Une boucle de rétroaction peut être ajoutée afin de modifier intelligemment la durée du cycle. On obtient alors ce que l'on appelle une boucle fermée, puisqu'une information sur l'état de sortie de notre système, obtenue à l'aide de capteurs, va être comparée à un signal de référence afin de nourir un contrôleur qui a la charge de choisir la bonne entrée. On peut ici parler d'asservissement.
Les boucles de contrôle d'attitude ont pour but d'assurer un contrôle stable de l'orientation du satellite, en prenant en compte les contraintes opérationnelles (temps de réponse aux commandes par exemple) et les perturbations externes et internes. On met en place un asservissement dans le but d'atteindre une valeur de consigne et de la maintenir. Pour ce faire, l'asservissement, ou correcteur, mesure en permanence l'écart entre la valeur réelle de la grandeur à asservir et la valeur de consigne. Il en déduit la commande appropriée que les actionneurs devront ensuite appliquer afin de réduire cet écart.
Systèmes linéaires
Un système linéaire est un objet qui peut être décrit par des équations linéaires. De tels systèmes sont essentiels car nous pouvons les résoudre. Pourtant, presque aucun système réel n'est un système linéaire. L'objectif est donc de simplifier l'objet étudié (actionneur, capteur, système dynamique...) afin de pouvoir l'approximer par un système linéaire. On parle alors de son domaine linéarité.
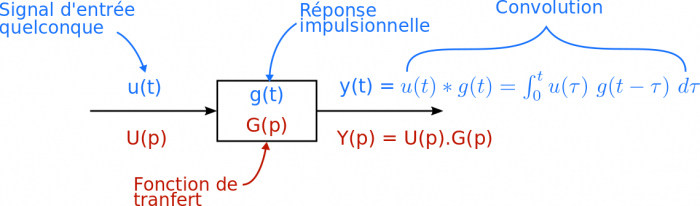
La réponse d'un système linéaire peut être obtenue en sommant ses réponses impulsionnelles. Cette sommation dans le domaine temporel est appelée convolution. Soit un signal d'entrée u(t) et une réponse impulsionnelle g(t), la sortie y(t) s'exprime :
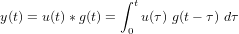
Représentation de la boucle de contrôle d'attitude
On représente la boucle du SCA comme un contrôle en boucle fermée, avec le terme de rétroaction. On note R(p) le signal de référence, Y(p) le signal de sortie, D(p) la perturbation, U(p) le signal de contrôle, Gc(p) le contrôleur, E(p) l'erreur, Gp(p) le matériel à contrôler et C(p) la dynamique des capteurs. Si l'on considère que les perturbations sont nulles, la fonction de transfert s'écrit :
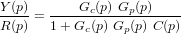
Le dénominateur de cette équation est un polynome dont les racines déterminent le type de réponse. Le contrôleur peut être utilisé pour stabiliser le système ou lui donner des caractéristiques particulières.
Boucle ouverte ou fermée
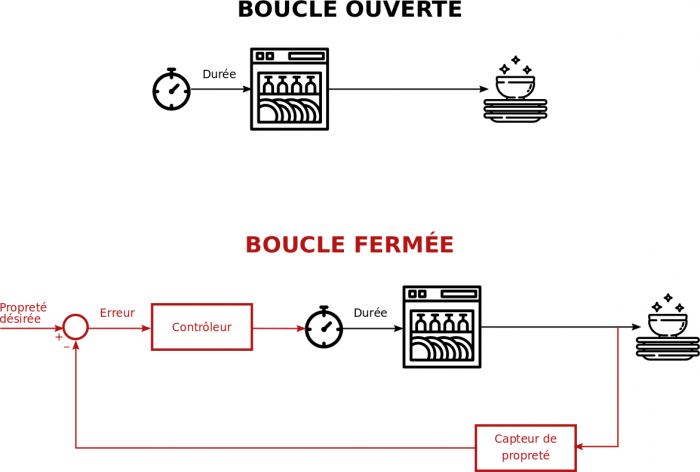
Dans la boucle ouverte, la durée du cycle de lavage ne dépend pas de la propreté de la vaisselle qu'il contient. Afin d'adapter cette durée à l'état des assiettes et verres, il faut qu'un capteur de propreté fournisse une information à comparer à la propretée désirée et qu'un contrôleur en déduise une nouvelle durée. C'est ce que l'on appelle une boucle fermée.
Crédit :
Gary Quinsac
Fonction de transfert
Crédit :
Gary Quinsac
Diagramme en bloc de la boucle de contrôle
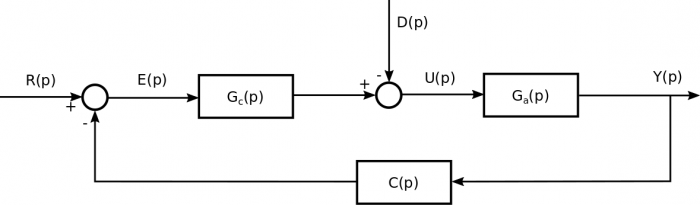
Chaque élément de la boucle de contrôle d'attitude est représenté par sa fonction de transfert.
Crédit :
"Fundamentals of Spacecraft Attitude Determination and Control", F. Landis Markley et John L. Crassidis.
Le contrôleur a pour objectif de convertir l'erreur, c'est-à-dire l'écart entre la mesure de la sortie de la boucle et le signal de référence, en un signal de contrôle qui va finir par ramener l'erreur à 0.
Les performances du contrôleur et a fortiori de l'asservissement sont décrites par plusieurs paramètres :
- la rapidité, qui définit la vitesse à laquelle une valeur de sortie stable est atteinte; la rapidité est caractérisée par le temps de réponse du système ;
- la stabilité, qui définit la capacité de l'asservissement à produire une sortie tendant vers une valeur finie pour une entrée constante (pas d'oscillation ou de divergence) ;
- le dépassement de la consigne, qui correspond au dépassement par la sortie de la valeur de consigne avant de se stabiliser ;
- la précision, c'est-à-dire la capacité de l'asservissement à atteindre la consigne avec précision le plus rapidement possible.
L'asservissement doit ainsi assurer un compromis entre performance et stabilité. La performance est proportionnelle à la valeur du gain du correcteur, mais à partir d'une certaine valeur celui-ci a tendance à déstabiliser le système.
Facteur d'amortissement
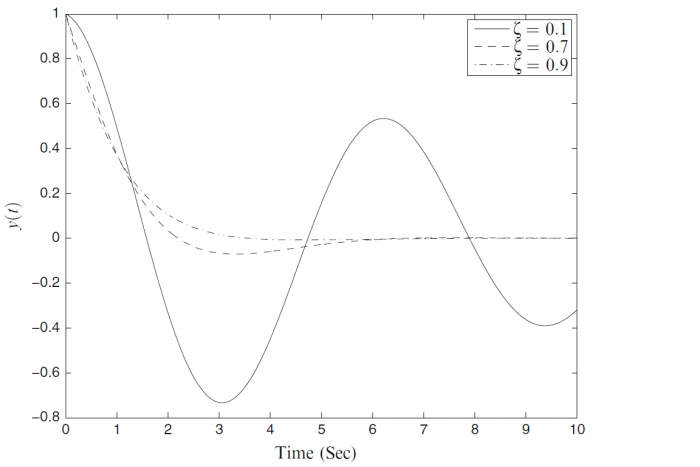
Réponse pour différents facteurs d'amortissement.
Crédit :
"Fundamentals of Spacecraft Attitude Determination and Control", F. Landis Markley et John L. Crassidis.

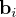 définissant la direction mesurée (observée) de la source (la Terre, le Soleil, une étoile, le champ magnétique terrestre...), exprimée dans le repère lié au satellite. Le second est un vecteur unitaire
définissant la direction mesurée (observée) de la source (la Terre, le Soleil, une étoile, le champ magnétique terrestre...), exprimée dans le repère lié au satellite. Le second est un vecteur unitaire 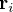 qui définit la direction de référence de la source, exprimée dans le repère origine (généralement inertiel). L'estimation d'attitude consiste ici à déterminer la matrice de transformation orthogonale
qui définit la direction de référence de la source, exprimée dans le repère origine (généralement inertiel). L'estimation d'attitude consiste ici à déterminer la matrice de transformation orthogonale  satisfaisant pour chaque observation i :
satisfaisant pour chaque observation i :
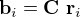
 permettant de transformer les vecteurs de référence
permettant de transformer les vecteurs de référence 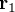 et
et 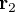 en vecteurs d'observation
en vecteurs d'observation 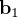 et
et 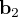 . Puisque l'on cherche à obtenir l'attitude suivant 3 axes, il nous faut créer deux bases orthonormées (y1, y2, y3) et (x1, x2, x3), respectivement associées aux vecteurs d'oservation et de référence. Il ne reste plus qu'à déduire la matrice de transformation orthogonale (ou MCD)
. Puisque l'on cherche à obtenir l'attitude suivant 3 axes, il nous faut créer deux bases orthonormées (y1, y2, y3) et (x1, x2, x3), respectivement associées aux vecteurs d'oservation et de référence. Il ne reste plus qu'à déduire la matrice de transformation orthogonale (ou MCD) 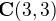 satisfaisant :
satisfaisant :
![\bold y_i = [C] \ \bold x_i](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation11.png) ,
, 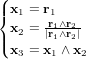 ,
, 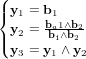
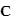 minimisant la fonction de moindres carrés :
minimisant la fonction de moindres carrés :
![L = \frac{1}{2} \ \sum_{i=1}^{n}{a_i \left| \bold b_i - [C] \bold r_i \right|^2}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation15.png)
![\bold x_k = [A]_k \ \bold x_{k-1} + [B]_k \ \bold u_{k-1} + \bold w_{k-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation16.png)
![\bold z_k = [H]_k \ \bold x_k + \bold v_k](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation17.png)
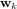 et
et 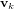 représentent respectivement les bruits de processus et de mesure. On les suppose indépendants, blancs et de distribution de probabilité normale.
représentent respectivement les bruits de processus et de mesure. On les suppose indépendants, blancs et de distribution de probabilité normale. ![[A]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation20.png) est la matrice qui relie l'état précédent k-1 à l'état actuel k,
est la matrice qui relie l'état précédent k-1 à l'état actuel k, ![[B]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation21.png) est la matrice qui relie l'entrée de commande
est la matrice qui relie l'entrée de commande  à l'état
à l'état  .
. ![[H]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation24.png) est la matrice reliant l'état
est la matrice reliant l'état  à sa mesure
à sa mesure  .
.
![\hat{\bold x}_{k|k-1} = [A]_k \ \hat{\bold x}_{k-1|k-1} + [B]_k \ \bold u_{k-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation27.png)
![[P]_{k|k-1} = [A]_k \ [P]_{k-1|k-1} \ {[A]_k}^T + [Q]_k](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation28.png)
![[Q]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation29.png) est la matrice de covariance du bruit de processus
est la matrice de covariance du bruit de processus 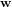 ,
, ![[P]_{k|k-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation31.png) est la matrice d'estimation a priori de la covariance de l'erreur.
est la matrice d'estimation a priori de la covariance de l'erreur.
![[K]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation32.png) , puis générer une estimation de l'état a posteriori en incorporant la mesure. Enfin, on obtient la matrice de covariance de l'erreur d'estimation a posteriori
, puis générer une estimation de l'état a posteriori en incorporant la mesure. Enfin, on obtient la matrice de covariance de l'erreur d'estimation a posteriori ![[P]_{k|k}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation33.png) .
.
![[K]_k = [P]_{k|k-1} {[H]_k}^T \ {[S]_k}^{-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation34.png)
![\hat{\bold x}_{k|k} = \hat{\bold x}_{k|k-1} + [K]_k \ \bold y_k](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation35.png)
![[P]_k = \left( [I] - [K]_k \ [H]_k \right) [P]_{k|k-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation36.png)
![[I]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation37.png) est la matrice identité. Deux équations supplémentaires permettent d'obtenir l'innovation, ou résiduel,
est la matrice identité. Deux équations supplémentaires permettent d'obtenir l'innovation, ou résiduel, 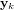 , et la covariance de l'innovation
, et la covariance de l'innovation ![[S]_k](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation39.png) :
:
![\bold y_k = \bold z_k - [H]_k \ \hat{\bold x}_{k|k-1}](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation40.png)
![[S]_k = [H]_k \ [P]_{k|k-1} \ {[H]_k}^T + [R]_k](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation41.png)
![[R]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation42.png) du bruit de mesure est déterminée avant d'utiliser le filtre et peut être mise à jour par la suite. Il est plus compliqué de déterminer la matrice de covariance du bruit de processus
du bruit de mesure est déterminée avant d'utiliser le filtre et peut être mise à jour par la suite. Il est plus compliqué de déterminer la matrice de covariance du bruit de processus ![[Q]](../pages_nanosats/equations_nanosats-comprendre-techniques-estimation-d-attitude/equation43.png) car nous ne pouvons généralement pas directement observer le processus à estimer. Afin d'améliorer les performances du filtre, il est habituel de régler ces deux paramètres.
car nous ne pouvons généralement pas directement observer le processus à estimer. Afin d'améliorer les performances du filtre, il est habituel de régler ces deux paramètres.
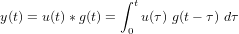
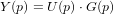
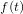 une fonction du temps. Sa transformée de Laplace unilatérale
une fonction du temps. Sa transformée de Laplace unilatérale 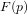 est
définie par
est
définie par 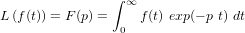 où
où 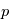 est la variable complexe.
est la variable complexe.
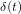 (Dirac)
(Dirac)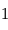
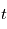
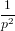
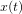
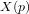
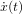
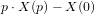
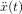
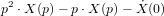
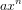
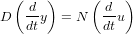 où
où 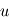 et
et 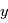 sont respectivement l'entrée et la sortie et
sont respectivement l'entrée et la sortie et 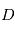 et
et 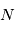 sont des polynômes à coefficients réels en (d/dt). Si l'on considère que les conditions initiales sont nulles, on peut réécrire l'équation différentielle précédente pour obtenir la fonction de transfert H :
sont des polynômes à coefficients réels en (d/dt). Si l'on considère que les conditions initiales sont nulles, on peut réécrire l'équation différentielle précédente pour obtenir la fonction de transfert H :
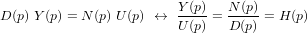
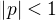 ).
).
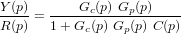



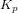
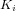
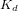
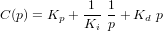
![[I] \ \ddot \theta (t) = u(t) + w(t)](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation30.png)
![[I]](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation31.png) est la matrice d'inertie,
est la matrice d'inertie, 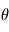 est l'angle,
est l'angle, 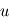 est le couple de contrôle et
est le couple de contrôle et 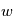 est le couple perturbateur extérieur.
est le couple perturbateur extérieur.
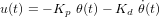
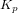 et
et 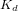 sont des gains qu'il faut déterminer. Le système en boucle fermée et son équation caractéristique s'écrivent alors :
sont des gains qu'il faut déterminer. Le système en boucle fermée et son équation caractéristique s'écrivent alors :
![[I] \ \ddot \theta (t) + [K_d] \ \dot \theta (t) + [K_p] \ \theta(t) = w(t) \ \leftrightarrow \ I \ p^2 + [K_d] \ p + [K_p] = 0](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation38.png)
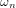 et
et 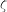 , respectivement la fréquence propre (fréquence de la réponse sinusoïdale du système non amorti) et le facteur d'amortissement. L'équation caractéristique est réécrite en introduisant ces deux nouvelles grandeurs :
, respectivement la fréquence propre (fréquence de la réponse sinusoïdale du système non amorti) et le facteur d'amortissement. L'équation caractéristique est réécrite en introduisant ces deux nouvelles grandeurs :
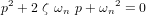
![[K_p] = [I] \ {\omega_n}^2](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation42.png) et
et ![[K_d] = 2 \ [I] \ \zeta \ \omega_n](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation43.png) . On choisit généralement le
. On choisit généralement le 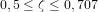 . Il est important de noter que l'information sur la dérivée provient de
. Il est important de noter que l'information sur la dérivée provient de 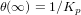 . Idéalement nous souhaitons que l'attitude en régime permanent soit nulle, c'est la raison pour laquelle nous introduisons le contrôleur PID (proportionnel-intégral-dérivé) :
. Idéalement nous souhaitons que l'attitude en régime permanent soit nulle, c'est la raison pour laquelle nous introduisons le contrôleur PID (proportionnel-intégral-dérivé) :
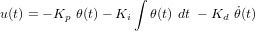
![[I] \ p^3 + [K_d] \ p^2 + [K_p] \ p + [K_i] = 0 \ \leftrightarrow \ \left( p^2 + 2 \ \zeta \ \omega_n \ p + {\omega_n}^2 \right) \left( p + \frac{1}{T} \right) = 0](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation47.png)
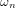 et
et 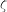 sont toujours la fréquence propre et le facteur d'amortissement, et
sont toujours la fréquence propre et le facteur d'amortissement, et 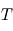 est la constante temporelle associée au contrôle intégral. Les gains du contrôleur PID s'expriment :
est la constante temporelle associée au contrôle intégral. Les gains du contrôleur PID s'expriment : ![[K_p] = [I] \left( {\omega_n}^2 + \frac{2 \ \zeta \ \omega_n}{T} \right)](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation51.png) ,
, ![[K_i] = [I] \ \frac{{\omega_n}^2}{T}](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation52.png) et
et ![[K_d] = [I] \left( 2 \ \zeta \ \omega_n + \frac{1}{T}\right)](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation53.png) . On choisit souvent la constante
. On choisit souvent la constante 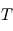 telle que :
telle que : 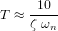 .
.
