Les faibles forces agissant sur un satellite sont connues pour dégrader la précision de pointage et engendrer des déformations mécaniques.
Des perturbations de différentes origines...
On peut distinguer les perturbations externes des perturbations internes au satellite. Dans la première catégorie on retrouve la pression de radiation solaire, la trainée atmosphérique ou pression dynamique, le couple magnétique dû au dipôle résiduel et le gradient de gravité. Les perturbations internes sont liées aux équipements présents dans le satellite. Si certains sont utilisés pour contrôler le satellite, comme les roues à inertie, la plupart sont à l'origine de couples perturbateurs. Parmi ces phénomènes, on retrouve les mécanismes tels que ceux utilisés pour les panneaux solaires ou les instruments mobiles, le désalignement et la quantification des actionneurs, le déplacement du carburant, l'incertitude sur le positionnement du centre de gravité, le frottement des roues à inertie ou encore le dégazage des polymères.
Les forces extérieures sont les plus importantes pour la majorité des CubeSats car ceux-ci sont généralement dépourvus de mécanismes ou de parties mobiles. On dénombre 4 sources environmentales de couples perturbateurs dont l'intensité varie grandement en fonction de la position du satellite dans l'espace :
Ayant différents effets
On remarque que les perturbations citées précédemment peuvent avoir deux types d'effets : séculaire ou cyclique. Les perturbations ayant un effet cyclique sont en moyenne nulles sur une orbite circulaire. Les perturbations séculaires s'accumulent durant une orbite et sont analogues à une force non-conservative. Or, on se souvient que les couples extérieurs sont proportionnels à la variation du moment cinétique du satellite. La gestion du moment cinétique va donc dépendre du type de perturbation auquel le satellite aura affaire. Suivant le pointage, certaines perturbations extérieures peuvent être cycliques ou séculaires. Dans le cas d'un pointage inertiel, on parle d'effets cycliques pour la traînée atmosphérique, le gradient de gravité et les couples magnétiques, alors qu'on parle d'effets séculaires pour les couples de pression de radiation solaire. Dans le cas d'un autre pointage classique, le pointage nadir, les couples magnétiques et de pression solaire ont des effets cycliques, à l'inverse de la trainée atmosphérique. Pour ce qui est des gradients de gravité, ils peuvent avoir les deux types d'effets.
Perturbations environmentales
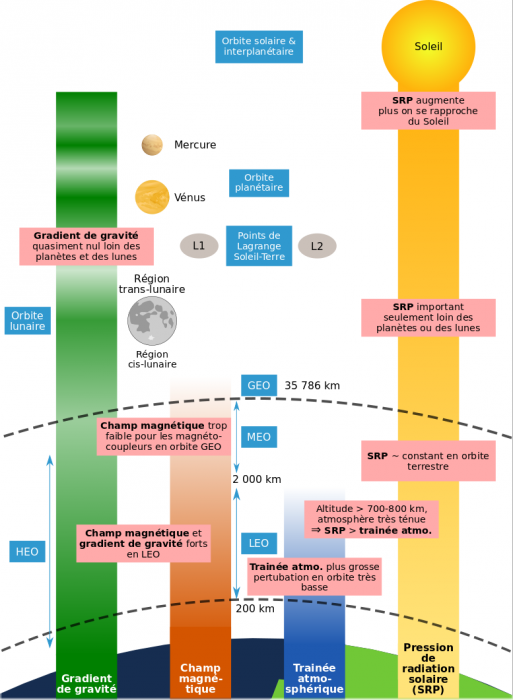
Couples perturbateurs dus à l'environement du satellite.
Crédit :
Gary Quinsac
Couples subis par un CubeSat de 3U
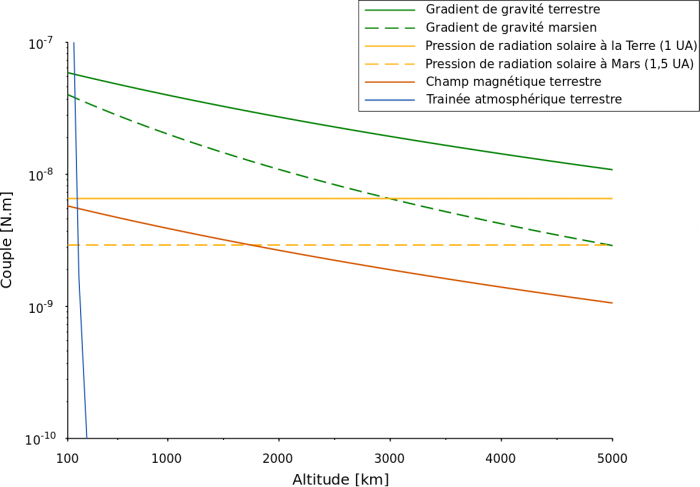
Les couples maximums subis par un CubeSat de 3U autour de la Terre et Mars sont représentés (respectivement en traits pleins et pointillés). Mars n'ayant pas ou peu de champ magnétique et une atmosphère très ténue, les couples associés ne sont pas représentés car trop faibles.
Crédit :
Gary Quinsac
Couple cyclique ou séculaire : fonction du pointage
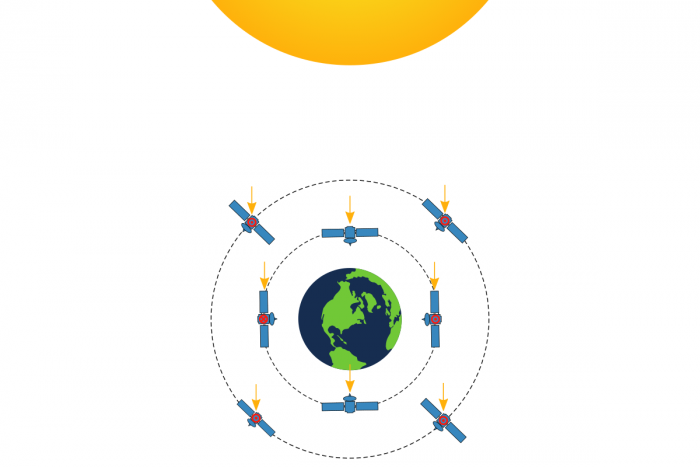
Le couple de pression de radiation solaire est plus ou moins constant dans le cas d'un pointage inertiel, à l'origine d'une accumulation du moment cinétique : c'est un couple séculaire. Au contraire, ce couple est moyennement nul sur une orbite pour un satellite effectuant un pointage nadir : on dit alors que le couple est cyclique.
Crédit :
Gary Quinsac
Gestion du moment cinétique
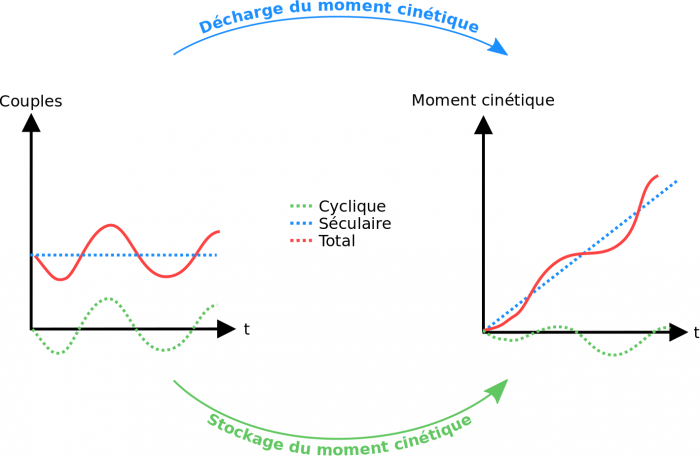
On peut voir l'accumulation du moment cinétique au cours d'une orbite dans le cas d'un couple séculaire, nécessitant de décharger celui-ci avec des actionneurs appropriés. En revanche le couple cyclique peut être stocké par un actionneur qui va se contenter de fournir un couple en opposition de phase tout au long de l'orbite.
Crédit :
Gary Quinsac
Certains corps célestes, dont la Terre, ont des champs magnétiques assez puissants pour induire d'importants effets dans l'espace environnant. Ce champ interagit avec tout autre champ magnétique qu'il rencontre. En général, les satellites ont eux-mêmes un certain niveau de moment magnétique résiduel qui se traduit par un champ magnétique propre relativement faible. Ils se comportent comme des dipôles magnétiques car ils sont parcourus par des boucles de courant. Ainsi, un courant de I ampères circulant dans une boucle plane d'aire A produit le moment dipolaire (en A.m) :
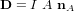
Des méthodes de compensation sont généralement mises en œuvre à bord. Si le moment magnétique résiduel d'un satellite n'est pas aligné avec le champ magnétique local un couple magnétique apparaît et modifie l'attitude du satellite. Le couple magnétique 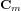 est donné par :
est donné par :
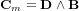
où 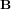 (en T) représente le champ magnétique.
(en T) représente le champ magnétique.
 Champ magnétique terrestre
Champ magnétique terrestre
Bien que le champ magnétique de la Terre soit complexe, il est souvent suffisant de le modéliser tel un dipôle (30% d'erreur sont souvent considérés) et de déterminer la valeur maximum possible. Le couple maximum peut donc être estimé à partir du champ magnétique 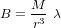 , où
, où 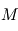 (en T.m3) est le moment magnétique terrestre multiplié par la constante magnétique,
(en T.m3) est le moment magnétique terrestre multiplié par la constante magnétique, 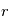 la distance entre le satellite et le centre du corps , et enfin
la distance entre le satellite et le centre du corps , et enfin 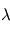 une fonction sans unité de la latitude magnétique qui prend des valeurs allant de 1 au niveau de l'équateur magnétique à 2 aux pôles magnétiques. Des modèles utilisant des harmoniques sphériques existent, à la manière du champ gravitationnel terrestre, mais la précision qu'ils permettent d'atteindre n'est pas nécessaire lors des premières phases de développement du projet spatial. L'un de ces modèles, le "12th generation of the International Geomagnetic Reference Field (IGRF)", est utilisé pour calculer le champ magnétique obtenu sur une trajectoire circulaire de 500 km d'altitude inclinée de 50°. Celui-ci est représenté par rapport au plan local tangent ou repère NED ("North East Down"). On remarque qu'il varie grandement au cours de l'orbite.
une fonction sans unité de la latitude magnétique qui prend des valeurs allant de 1 au niveau de l'équateur magnétique à 2 aux pôles magnétiques. Des modèles utilisant des harmoniques sphériques existent, à la manière du champ gravitationnel terrestre, mais la précision qu'ils permettent d'atteindre n'est pas nécessaire lors des premières phases de développement du projet spatial. L'un de ces modèles, le "12th generation of the International Geomagnetic Reference Field (IGRF)", est utilisé pour calculer le champ magnétique obtenu sur une trajectoire circulaire de 500 km d'altitude inclinée de 50°. Celui-ci est représenté par rapport au plan local tangent ou repère NED ("North East Down"). On remarque qu'il varie grandement au cours de l'orbite.
Dipôle magnétique terrestre
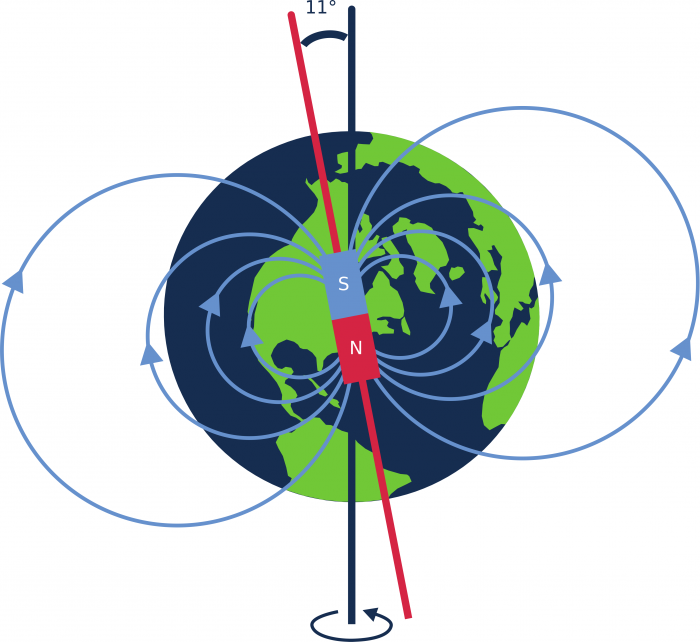
La Terre peut être assimilée à un dipôle magnétique dont l'axe est incliné d'à peu près 11° par rapport à l'axe nord-sud géographique. Attention, le pôle sud magnétique se trouve du coté du pôle nord géographique.
Crédit :
Gary Quinsac
Champ magnétique terrestre sur une orbite
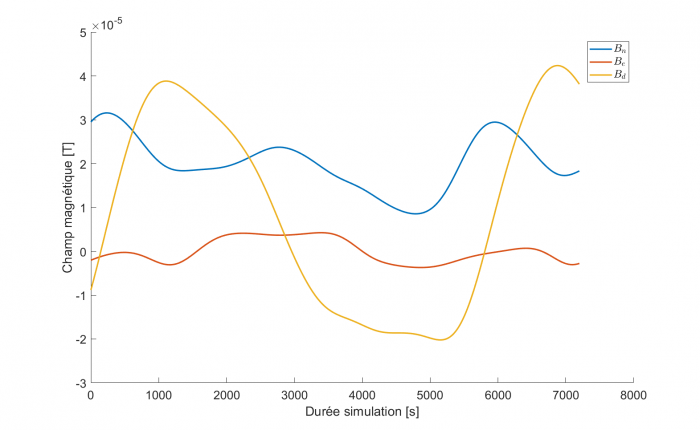
Champ magnétique sur une orbite terrestre circulaire de 500 km d'altitude et 50° d'inclinaison dans le référentiel NED.
Crédit :
Gary Quinsac
En dehors de quelques corps du système solaire, tels que la Terre et Jupiter, la plupart des régions de l'espace ne possèdent pas un champ magnétique suffisamment puissant et bien connu pour qu'un contrôle d'attitude magnétique puisse être utilisé par un satellite s'y trouvant.
 Aller plus loin
Aller plus loin
Le gradient de gravité résulte de l'interaction du champ gravitationnel, lui-même proportionnel à l'inverse du carré de la distance, avec un satellite de masse non ponctuelle. L'accélération gravitationnelle est la plus forte sur la partie du satellite la plus proche du corps attracteur. Le gradient est à l'origine d'un couple qui peut être utilisé pour contrôler passivement l'attitude du satellite. Les couples de gradient de gravité apparaissent lorsque le centre de gravité d'un satellite en orbite n'est pas aligné avec le centre de masse par rapport à la verticale locale.
 Centres de masse et de gravité
Centres de masse et de gravité
Le centre de masse, également appelé centre d'inertie, est le barycentre des masses d'un objet. Le centre de gravité, quant à lui, est le point d'application de la résultante des forces de gravité. Si ceux-ci sont souvent confondus, ce n'est plus le cas lorsque le champ de gravitation n'est plus uniforme dans le corps en question.
On exprime le gradient de gravité 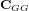 de la manière suivante :
de la manière suivante :
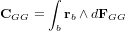
où 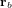 est le vecteur position allant du centre de gravité du satellite à l'élément de masse et
est le vecteur position allant du centre de gravité du satellite à l'élément de masse et 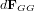 est la force de gravité s'appliquant sur ce même élément de masse :
est la force de gravité s'appliquant sur ce même élément de masse :
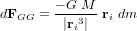
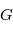 est la constante gravitationnelle, elle vaut
est la constante gravitationnelle, elle vaut 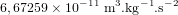 ,
, 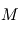 est la masse du corps attracteur et
est la masse du corps attracteur et 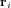 est le vecteur position de l'élément de masse
est le vecteur position de l'élément de masse 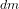 dans le référentiel inertiel (
dans le référentiel inertiel (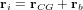 ). On peut finalement réécrire l'équation donnant le couple de gradient de gravité de la manière suivante :
). On peut finalement réécrire l'équation donnant le couple de gradient de gravité de la manière suivante :
![\bold C_{GG} = \frac{3 \ G \ M}{|\bold r_{CG}|^5} \ \bold r_{CG} \wedge \left([I] \ \bold r_{CG} \right)](../pages_nanosats/equations_nanosats-comprendre-perturbations-perturbations-externes/equation20.png)
Ce couple dépend de la matrice d'inertie ![[I]](../pages_nanosats/equations_nanosats-comprendre-perturbations-perturbations-externes/equation21.png) du satellite. Différentes propriétés sont visibles dans cette équation : la magnitude est inversement proportionnelle au cube de la distance au centre du corps attracteur, sa direction est perpendiculaire au rayon vecteur et il disparaît lorsque l'un des axes principaux du satellite est aligné avec ce rayon vecteur.
du satellite. Différentes propriétés sont visibles dans cette équation : la magnitude est inversement proportionnelle au cube de la distance au centre du corps attracteur, sa direction est perpendiculaire au rayon vecteur et il disparaît lorsque l'un des axes principaux du satellite est aligné avec ce rayon vecteur.
 Stabilisation par gradient de gravité
Stabilisation par gradient de gravité
Cette technique de contrôle d'attitude passive est assez utilisée pour des satellites en orbite terrestre devant pointer au nadir. Elle consiste à faire intéragir un satellite de forme particulière avec le champ gravitationnel afin de contraindre son orientation. Une masse peut être montée au bout d'un mât perpandiculaire à l'orbite afin de créer un moment d'inertie minimum selon cet axe. Cette masse étant plus proche, elle est plus attirée. Le satellite aura alors tendance à aligner cet axe d'inertie vers la verticale à l'orbite (qui est la direction d'attraction gravitationnelle).
 Aller plus loin
Aller plus loin
Gradient de gravité
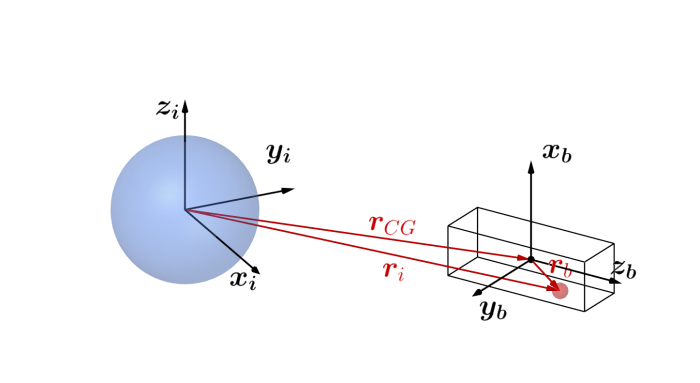
Géométrie du couple de gradient de gravité.
Crédit :
Gary Quinsac
Satellite stabilisé par gradient de gravité
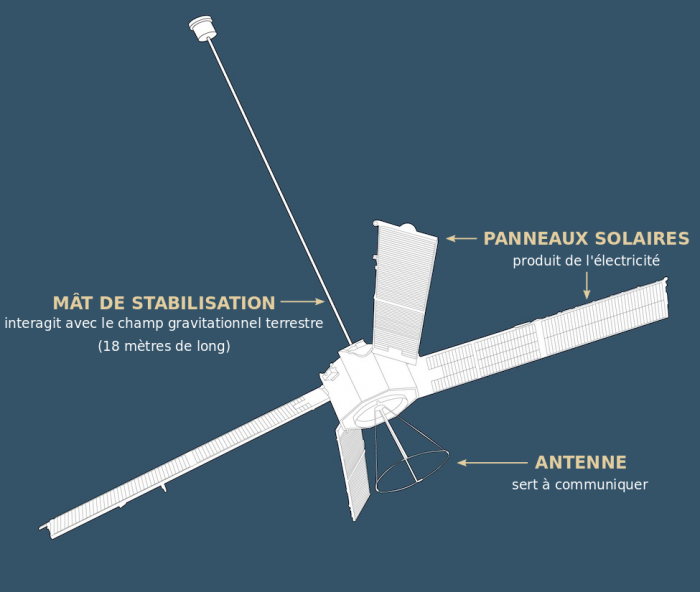
Crédit :
National Air and Space Museum, Smithsonian Institution.
La pression de radiation solaire est la source dominante de couples perturbateurs dans l'espace interplanétaire (absence de traînée atmosphérique, faibles champs de gravité et magnétique). Même en orbite basse, on a pour habitude de considérer qu'il est dominant à des altitudes supérieures à 800 km. Il est important de noter que si le Soleil n'est pas l'unique source de radiation (il y a notamment l'albédo de la Terre et de la Lune, les rayons cosmiques...), il est de loin la plus importante. Le Soleil émet des photons, mais également des protons et des électrons (vent solaire). L'interaction entre la lumière du Soleil et la surface du satellite est habituellement modélisée comme une force de pression exercée sur un objet.
On modélise la surface du satellite comme une collection de 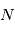 surfaces d'aire
surfaces d'aire 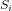 , dont la normale orientée vers l'extérieur est notée
, dont la normale orientée vers l'extérieur est notée 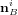 dans le référentiel du satellite et de coefficient de réflexion
dans le référentiel du satellite et de coefficient de réflexion 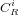 (on lui attribue généralement une valeur de 0,6 pour un petit satellite).
(on lui attribue généralement une valeur de 0,6 pour un petit satellite).
Le vecteur allant du satellite au Soleil dans le référentiel du satellite s'écrit 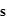 . L'angle entre ce vecteur et et la normale à la ième surface s'écrit alors :
. L'angle entre ce vecteur et et la normale à la ième surface s'écrit alors :
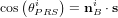
La force de pression de radiation solaire exercée sur une surface peut alors s'exprimer de la manière suivante :
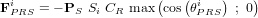 avec
avec 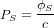
où 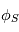 (en W.m) est l'irradiance solaire moyenne (fonction de la distance au Soleil) et
(en W.m) est l'irradiance solaire moyenne (fonction de la distance au Soleil) et 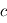 (en m/s) est la vitesse de la lumière.
(en m/s) est la vitesse de la lumière.
La différence entre les positions des centres de pression solaire et de masse aboutit à un couple de radiation solaire. Une telle différence dépend des surfaces éclairées, de l'incidence des rayons lumineux et de la répartition de la masse à l'intérieur du satellite. On note 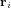 le vecteur allant du centre de masse du satellite au centre de pression de radiation solaire de la ième surface. Le couple de radiation solaire s'écrit alors :
le vecteur allant du centre de masse du satellite au centre de pression de radiation solaire de la ième surface. Le couple de radiation solaire s'écrit alors :
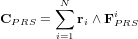
 Complément : coefficients de réflexion
Complément : coefficients de réflexion
Afin de gagner en précision, il est possible de détailler le coefficient de réflexion en une somme de trois coefficients dont le résultat vaut 1 :
La force de pression de radiation sur la ième surface s'exprime alors :
![\bold F_{PRS}^i = -P_S \ S_i \left[ 2 \left( \frac{R_{diff}^i}{3} + R_{spec}^i \ \textup{cos} \left(\theta_{PRS}^i \right) \right) \bold n_B^i + \left( 1-R_{spec}^i \right) \bold s \right] \textup{max} \left( \textup{cos} \left( \theta_{PRS}^i \right) \ ; \ 0 \right)](../pages_nanosats/equations_nanosats-comprendre-perturbations-perturbations-externes/equation37.png)
 Zone d'ombre
Zone d'ombre
Afin de simuler la pression de radiation solaire, il ne faut pas oublier les zones d'ombres dans lesquelles le satellite peut se retrouver. Par exemple, en orbite basse autour de la Terre, un satellite peut passer une partie importante de son orbite caché des rayons du Soleil. L'approche la plus simple est de considérer que l'ombre de la Terre est une projection cylindrique du diamètre de la Terre le long de l'axe Soleil-Terre. Sur cette figure on remarque qu'en faisant le produit scalaire de vecteur unitaire 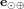 (Terre-Soleil) on obtient l'inégalité suivante lorsque le satellite se trouve dans la zone d'ombre :
(Terre-Soleil) on obtient l'inégalité suivante lorsque le satellite se trouve dans la zone d'ombre :
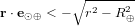
Géométrie du couple de pression de radiation solaire
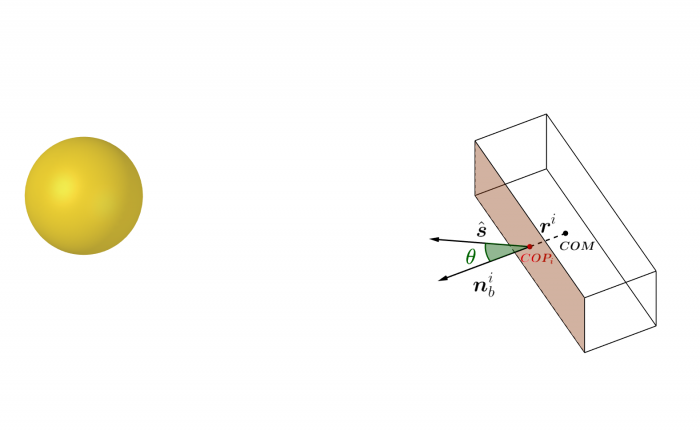
Géométrie du couple de pression de radiation solaire. Chaque face du satellite exposée au Soleil subit une force qui, si elle est désaxée par rapport au centre de masse, engendre un couple.
Crédit :
Gary Quinsac
Zones d'ombre
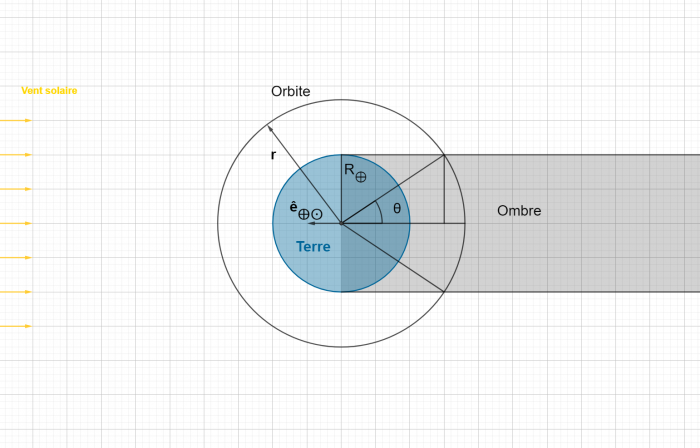
Géométrie simplifiée du problème de zone d'ombre en orbite terrestre.
Crédit :
Gary Quinsac
L'atmosphère ténue des corps célestes peut exercer une force de pression sur un satellite. Cela inclut toutes les interactions avec des particules non-chargées, comme les queues de comète, les poussières ou les éjectas. Dans le cas de la Terre, à quelques centaines de kilomètres d'altitude, ce couple peut être le plus important. De la même manière qu'avec le couple dû à la pression de radiation solaire, on calcule la force exercée par la traînée atmosphérique en considérant que le satellite est une collection de N surfaces d'aire Si. On définit de nouveau la normale orientée vers l'extérieur, notée 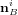 , pour chacune des surfaces. La force s'exerçant sur chaque surface dépend de la vitesse relative du satellite par rapport à l'atmosphère. En première approximation, on considère que cette vitesse relative est égale à celle du satellite, mais en réalité ce n'est pas immédiatement la vitesse du satellite dans le référentiel inertiel, car l'atmosphère n'est pas stationnaire dans celui-ci. L'inclinaison de la ième surface par rapport à la vitesse relative du satellite s'exprime :
, pour chacune des surfaces. La force s'exerçant sur chaque surface dépend de la vitesse relative du satellite par rapport à l'atmosphère. En première approximation, on considère que cette vitesse relative est égale à celle du satellite, mais en réalité ce n'est pas immédiatement la vitesse du satellite dans le référentiel inertiel, car l'atmosphère n'est pas stationnaire dans celui-ci. L'inclinaison de la ième surface par rapport à la vitesse relative du satellite s'exprime :
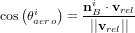
La force aérodynamique s'exerçant sur la ième surface est :
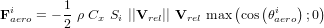
Dans cette équation, ρ est la densité atmosphérique et 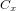 est le coefficient de trainée. Ce coefficient est déterminé de manière empirique et se situe généralement entre 1.5 et 2.5. Un couple apparaît lorsque la force agissant sur le centre de la pression atmosphérique ne passe pas par le centre de masse. Une estimation de ce couple est donnée par l'équation suivante :
est le coefficient de trainée. Ce coefficient est déterminé de manière empirique et se situe généralement entre 1.5 et 2.5. Un couple apparaît lorsque la force agissant sur le centre de la pression atmosphérique ne passe pas par le centre de masse. Une estimation de ce couple est donnée par l'équation suivante :
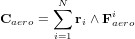
où 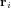 est le vecteur allant du centre de masse du satellite au centre de pression de la ième surface.
est le vecteur allant du centre de masse du satellite au centre de pression de la ième surface.
En principe, les couples aérodynamiques peuvent être utilisés pour effectuer un contrôle passif de l'attitude, comme les plumes d'une flèche, et même pour un contrôle actif avec des surfaces amovibles.
Bien que les CubeSats puissent généralement être modélisés comme un simple corps solide, de nombreuses raisons peuvent rendre la situation beaucoup plus complexe :
- Certains satellites peuvent être composés de nombreux corps solides en mouvement de rotation ou de translation les uns par rapport aux autres. La dynamique des corps flexibles utilise généralement des méthodes de calcul par éléments finis. Parmi les raisons simples empêchant de traiter un satellite comme un corps rigide, on peut citer la présence de roues à inertie, de gyroscopes, de panneaux solaires motorisés ou de systèmes de déploiement.
- Le déplacement des fluides, tels que le carburant ou les fluides cryogéniques est également une source de perturbations internes.
- Les désalignements et la quantification des actionneurs peut aussi être une source de perturbations. Par exemple, un système de propulsion dont l'axe de poussée serait décalé par rapport à l'axe idéal créera des couples non désirés à chaque fois qu'il sera utilisé.
On qualifie ces couples internes de couples d'échange de moment cinétique car ils correspondent à un échange de moment cinétique entre des composants d'un satellite complexe sans que le moment cinétique du satellite dans son ensemble ne soit modifié.




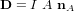
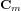 est donné par :
est donné par :
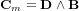
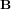 (en T) représente le champ magnétique.
(en T) représente le champ magnétique.
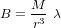 , où
, où 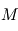 (en T.m3) est le moment magnétique terrestre multiplié par la constante magnétique,
(en T.m3) est le moment magnétique terrestre multiplié par la constante magnétique, 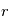 la distance entre le satellite et le centre du corps , et enfin
la distance entre le satellite et le centre du corps , et enfin 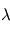 une fonction sans unité de la latitude magnétique qui prend des valeurs allant de 1 au niveau de l'équateur magnétique à 2 aux pôles magnétiques. Des modèles utilisant des harmoniques sphériques existent, à la manière du champ gravitationnel terrestre, mais la précision qu'ils permettent d'atteindre n'est pas nécessaire lors des premières phases de développement du projet spatial. L'un de ces modèles, le "12th generation of the International Geomagnetic Reference Field (IGRF)", est utilisé pour calculer le champ magnétique obtenu sur une trajectoire circulaire de 500 km d'altitude inclinée de 50°. Celui-ci est représenté par rapport au plan local tangent ou repère NED ("North East Down"). On remarque qu'il varie grandement au cours de l'orbite.
une fonction sans unité de la latitude magnétique qui prend des valeurs allant de 1 au niveau de l'équateur magnétique à 2 aux pôles magnétiques. Des modèles utilisant des harmoniques sphériques existent, à la manière du champ gravitationnel terrestre, mais la précision qu'ils permettent d'atteindre n'est pas nécessaire lors des premières phases de développement du projet spatial. L'un de ces modèles, le "12th generation of the International Geomagnetic Reference Field (IGRF)", est utilisé pour calculer le champ magnétique obtenu sur une trajectoire circulaire de 500 km d'altitude inclinée de 50°. Celui-ci est représenté par rapport au plan local tangent ou repère NED ("North East Down"). On remarque qu'il varie grandement au cours de l'orbite.


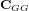 de la manière suivante :
de la manière suivante :
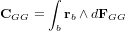
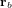 est le vecteur position allant du centre de gravité du satellite à l'élément de masse et
est le vecteur position allant du centre de gravité du satellite à l'élément de masse et 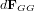 est la force de gravité s'appliquant sur ce même élément de masse :
est la force de gravité s'appliquant sur ce même élément de masse :
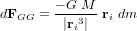
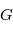 est la constante gravitationnelle, elle vaut
est la constante gravitationnelle, elle vaut 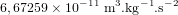 ,
, 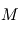 est la masse du corps attracteur et
est la masse du corps attracteur et 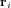 est le vecteur position de l'élément de masse
est le vecteur position de l'élément de masse 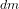 dans le référentiel inertiel (
dans le référentiel inertiel (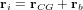 ). On peut finalement réécrire l'équation donnant le couple de gradient de gravité de la manière suivante :
). On peut finalement réécrire l'équation donnant le couple de gradient de gravité de la manière suivante :
![\bold C_{GG} = \frac{3 \ G \ M}{|\bold r_{CG}|^5} \ \bold r_{CG} \wedge \left([I] \ \bold r_{CG} \right)](../pages_nanosats/equations_nanosats-comprendre-perturbations-perturbations-externes/equation20.png)
![[I]](../pages_nanosats/equations_nanosats-comprendre-perturbations-perturbations-externes/equation21.png) du satellite. Différentes propriétés sont visibles dans cette équation : la magnitude est inversement proportionnelle au cube de la distance au centre du corps attracteur, sa direction est perpendiculaire au rayon vecteur et il disparaît lorsque l'un des axes principaux du satellite est aligné avec ce rayon vecteur.
du satellite. Différentes propriétés sont visibles dans cette équation : la magnitude est inversement proportionnelle au cube de la distance au centre du corps attracteur, sa direction est perpendiculaire au rayon vecteur et il disparaît lorsque l'un des axes principaux du satellite est aligné avec ce rayon vecteur.


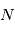 surfaces d'aire
surfaces d'aire 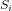 , dont la normale orientée vers l'extérieur est notée
, dont la normale orientée vers l'extérieur est notée 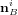 dans le référentiel du satellite et de coefficient de réflexion
dans le référentiel du satellite et de coefficient de réflexion 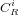 (on lui attribue généralement une valeur de 0,6 pour un petit satellite).
(on lui attribue généralement une valeur de 0,6 pour un petit satellite).
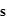 . L'angle entre ce vecteur et et la normale à la ième surface s'écrit alors :
. L'angle entre ce vecteur et et la normale à la ième surface s'écrit alors :
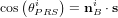
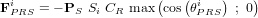 avec
avec 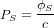
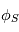 (en W.m) est l'irradiance solaire moyenne (fonction de la distance au Soleil) et
(en W.m) est l'irradiance solaire moyenne (fonction de la distance au Soleil) et 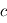 (en m/s) est la vitesse de la lumière.
(en m/s) est la vitesse de la lumière.
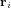 le vecteur allant du centre de masse du satellite au centre de pression de radiation solaire de la ième surface. Le couple de radiation solaire s'écrit alors :
le vecteur allant du centre de masse du satellite au centre de pression de radiation solaire de la ième surface. Le couple de radiation solaire s'écrit alors :
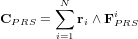
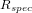 ;
;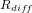 ;
;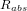 .
.![\bold F_{PRS}^i = -P_S \ S_i \left[ 2 \left( \frac{R_{diff}^i}{3} + R_{spec}^i \ \textup{cos} \left(\theta_{PRS}^i \right) \right) \bold n_B^i + \left( 1-R_{spec}^i \right) \bold s \right] \textup{max} \left( \textup{cos} \left( \theta_{PRS}^i \right) \ ; \ 0 \right)](../pages_nanosats/equations_nanosats-comprendre-perturbations-perturbations-externes/equation37.png)
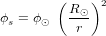
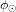 le flux émis à la surface du Soleil et
le flux émis à la surface du Soleil et 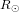 le rayon du Soleil.
le rayon du Soleil. 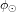 est estimé en appliquant la loi de Stefan-Boltzmann au Soleil considéré comme un corps noir :
est estimé en appliquant la loi de Stefan-Boltzmann au Soleil considéré comme un corps noir :
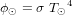
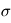 la constante de Stefan-Boltzmann et
la constante de Stefan-Boltzmann et 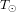 la température thermodynamique du corps noir. À la distance moyenne Terre-Soleil (1 UA) l'irradiance solaire (ou constante solaire) vaut 1362 W.m-2.
la température thermodynamique du corps noir. À la distance moyenne Terre-Soleil (1 UA) l'irradiance solaire (ou constante solaire) vaut 1362 W.m-2.
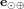 (Terre-Soleil) on obtient l'inégalité suivante lorsque le satellite se trouve dans la zone d'ombre :
(Terre-Soleil) on obtient l'inégalité suivante lorsque le satellite se trouve dans la zone d'ombre :
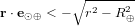


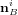 , pour chacune des surfaces. La force s'exerçant sur chaque surface dépend de la vitesse relative du satellite par rapport à l'atmosphère. En première approximation, on considère que cette vitesse relative est égale à celle du satellite, mais en réalité ce n'est pas immédiatement la vitesse du satellite dans le référentiel inertiel, car l'atmosphère n'est pas stationnaire dans celui-ci. L'inclinaison de la ième surface par rapport à la vitesse relative du satellite s'exprime :
, pour chacune des surfaces. La force s'exerçant sur chaque surface dépend de la vitesse relative du satellite par rapport à l'atmosphère. En première approximation, on considère que cette vitesse relative est égale à celle du satellite, mais en réalité ce n'est pas immédiatement la vitesse du satellite dans le référentiel inertiel, car l'atmosphère n'est pas stationnaire dans celui-ci. L'inclinaison de la ième surface par rapport à la vitesse relative du satellite s'exprime :
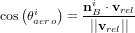
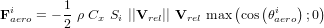
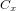 est le coefficient de trainée. Ce coefficient est déterminé de manière empirique et se situe généralement entre 1.5 et 2.5. Un couple apparaît lorsque la force agissant sur le centre de la pression atmosphérique ne passe pas par le centre de masse. Une estimation de ce couple est donnée par l'équation suivante :
est le coefficient de trainée. Ce coefficient est déterminé de manière empirique et se situe généralement entre 1.5 et 2.5. Un couple apparaît lorsque la force agissant sur le centre de la pression atmosphérique ne passe pas par le centre de masse. Une estimation de ce couple est donnée par l'équation suivante :
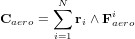
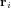 est le vecteur allant du centre de masse du satellite au centre de pression de la ième surface.
est le vecteur allant du centre de masse du satellite au centre de pression de la ième surface.