Contrôleur

Auteur: Gary Quinsac

Facteur d'amortissement

Réponse pour différents facteurs d'amortissement.

Crédit : "Fundamentals of Spacecraft Attitude Determination and Control", F. Landis Markley et John L. Crassidis.

Le contrôleur a pour objectif de convertir l'erreur, c'est-à-dire l'écart entre la mesure de la sortie de la boucle et le signal de référence, en un signal de contrôle qui va finir par ramener l'erreur à 0.

Les performances du contrôleur et a fortiori de l'asservissement sont décrites par plusieurs paramètres :

la rapidité, qui définit la vitesse à laquelle une valeur de sortie stable est atteinte; la rapidité est caractérisée par le temps de réponse du système ;
la stabilité, qui définit la capacité de l'asservissement à produire une sortie tendant vers une valeur finie pour une entrée constante (pas d'oscillation ou de divergence) ;
le dépassement de la consigne, qui correspond au dépassement par la sortie de la valeur de consigne avant de se stabiliser ;
la précision, c'est-à-dire la capacité de l'asservissement à atteindre la consigne avec précision le plus rapidement possible.

L'asservissement doit ainsi assurer un compromis entre performance et stabilité. La performance est proportionnelle à la valeur du gain du correcteur, mais à partir d'une certaine valeur celui-ci a tendance à déstabiliser le système.

Contrôleur PID

Le contrôleur "Proportionnel-Intégral-Dérivé" est la logique de contrôle la plus utilisée pour les régulateurs avec boucle de rétroaction. Ce contrôleur agit de trois manières :

action proportionnelle : l'erreur est multipliée par un gain
action intégrale : l'erreur est intégrée et divisée par un gain
action dérivée : l'erreur est dérivée et multipliée par un gain

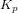
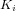
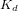
La fonction de transfert d'un régulateur PID s'exprime :

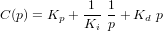
$C(p) = K_p + \frac{1}{K_i} \ \frac{1}{p} +K_d \ p$

Considérons un système de contrôle d'attitude mono-axe simple. L'équation d'Euler s'exprime :

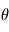$[I] \ \ddot \theta (t) = u(t) + w(t)$

où [I] est la matrice d'inertie, $\theta$ est l'angle, 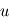est le couple de contrôle et 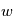est le couple perturbateur extérieur.

Contrôleur PD

Un simple contrôle proportionnel ne pourrait pas atteindre une réponse asymptotiquement stable, nous introduisons donc un régulateur PD (proportionnel-dérivé) :

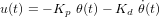
$u(t) = -K_p \ \theta(t) - K_d \ \dot \theta (t)$

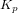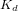où K_p et K_d sont des gains qu'il faut déterminer. Le système en boucle fermée et son équation caractéristique s'écrivent alors :

$[I] \ \ddot \theta (t) + [K_d] \ \dot \theta (t) + [K_p] \ \theta(t) = w(t) \ \leftrightarrow \ I \ p^2 + [K_d] \ p + [K_p] = 0$

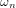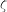Dans le but d'identifier les valeurs des deux gains, nous introduisons $\omega_n$ et $\zeta$ , respectivement la fréquence propre (fréquence de la réponse sinusoïdale du système non amorti) et le facteur d'amortissement. L'équation caractéristique est réécrite en introduisant ces deux nouvelles grandeurs :

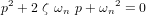
$p^2 + 2 \ \zeta \ \omega_n \ p + {\omega_n}^2 = 0$

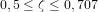Les gains du contrôleur s'expriment alors : $[K_p] = [I] \ {\omega_n}^2$ et $[K_d] = 2 \ [I] \ \zeta \ \omega_n$ . On choisit généralement le facteur d'amortissement de tel sorte que $0,5 \leq \zeta \leq 0,707$ . Il est important de noter que l'information sur la dérivée provient de gyroscopes ou de différences finies de l'attitude.

Contrôleur PID

Pour une perturbation constante de valeur unitaire, le système asservi par le contrôleur PD produit une attitude en régime permanent non-nulle : 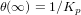$\theta(\infty) = 1/K_p$ . Idéalement nous souhaitons que l'attitude en régime permanent soit nulle, c'est la raison pour laquelle nous introduisons le contrôleur PID (proportionnel-intégral-dérivé) :

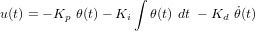
$u(t) = -K_p \ \theta(t) - K_i \int{\theta(t) \ dt} \ - K_d \ \dot \theta(t)$

L'équation caractéristique s'écrit cette fois :

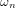$[I] \ p^3 + [K_d] \ p^2 + [K_p] \ p + [K_i] = 0 \ \leftrightarrow \ \left( p^2 + 2 \ \zeta \ \omega_n \ p + {\omega_n}^2 \right) \left( p + \frac{1}{T} \right) = 0$

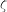où $\omega_n$ et $\zeta$ sont toujours la fréquence propre et le facteur d'amortissement, et 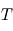est la constante temporelle associée au contrôle intégral. Les gains du contrôleur PID s'expriment : $[K_p] = [I] \left( {\omega_n}^2 + \frac{2 \ \zeta \ \omega_n}{T} \right)$ , $[K_i] = [I] \ \frac{{\omega_n}^2}{T}$ et $[K_d] = [I] \left( 2 \ \zeta \ \omega_n + \frac{1}{T}\right)$ . 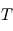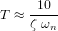On choisit souvent la constante telle que : $T \approx \frac{10}{\zeta \ \omega_n}$ .