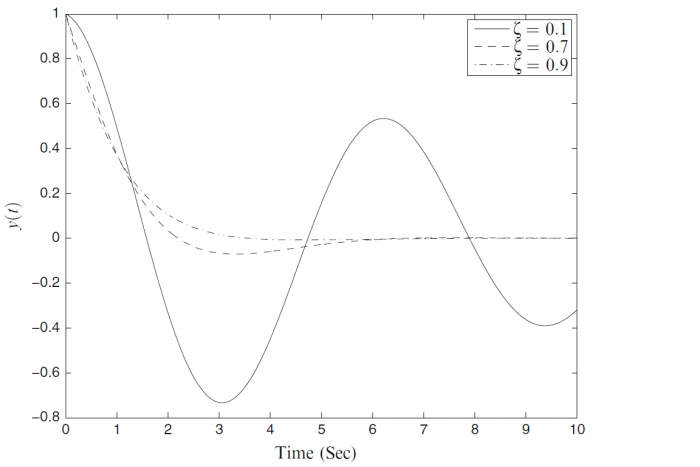
La théorie du contrôle s'intéresse au comportement de systèmes dynamiques en fonction de leurs paramètres. Elle peut être vue comme une stratégie permettant de sélectionner la bonne entrée d'un système pour que le sortie soit celle désirée. Cela fait partie du domaine de l'automatique.
Boucles ouvertes et fermées
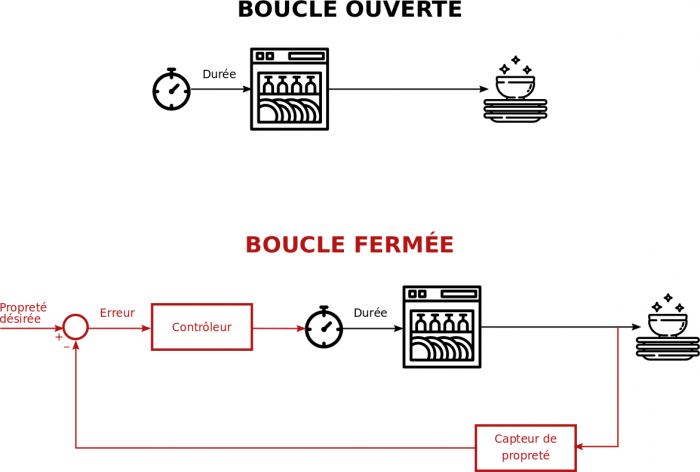
Un système de contrôle est un mécanisme altérant l'état futur d'un système. En l'absence de retour d'information concernant la sortie du système, on se trouve dans le cas d'une boucle ouverte. Prenons l'exemple d'un lave-vaisselle. Celui-ci est programmé pour tourner un certain temps, à une certaine température et avec une certaine quantité d'eau. Ces paramètres ne dépendent pas de l'état de la vaisselle qu'il contient.
Une boucle de rétroaction peut être ajoutée afin de modifier intelligemment la durée du cycle. On obtient alors ce que l'on appelle une boucle fermée, puisqu'une information sur l'état de sortie de notre système, obtenue à l'aide de capteurs, va être comparée à un signal de référence afin de nourir un contrôleur qui a la charge de choisir la bonne entrée. On peut ici parler d'asservissement.
Les boucles de contrôle d'attitude ont pour but d'assurer un contrôle stable de l'orientation du satellite, en prenant en compte les contraintes opérationnelles (temps de réponse aux commandes par exemple) et les perturbations externes et internes. On met en place un asservissement dans le but d'atteindre une valeur de consigne et de la maintenir. Pour ce faire, l'asservissement, ou correcteur, mesure en permanence l'écart entre la valeur réelle de la grandeur à asservir et la valeur de consigne. Il en déduit la commande appropriée que les actionneurs devront ensuite appliquer afin de réduire cet écart.
Systèmes linéaires
Un système linéaire est un objet qui peut être décrit par des équations linéaires. De tels systèmes sont essentiels car nous pouvons les résoudre. Pourtant, presque aucun système réel n'est un système linéaire. L'objectif est donc de simplifier l'objet étudié (actionneur, capteur, système dynamique...) afin de pouvoir l'approximer par un système linéaire. On parle alors de son domaine linéarité.
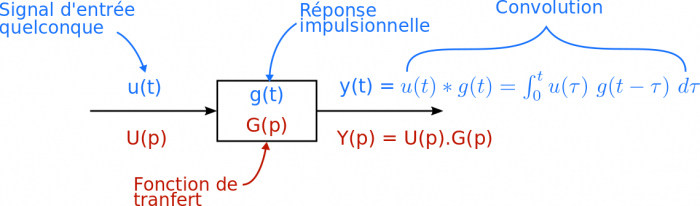
La réponse d'un système linéaire peut être obtenue en sommant ses réponses impulsionnelles. Cette sommation dans le domaine temporel est appelée convolution. Soit un signal d'entrée u(t) et une réponse impulsionnelle g(t), la sortie y(t) s'exprime :
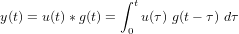
Fonction de transfert
Afin de simplifier cette opération, on introduit la fonction de transfert. Une fonction de transfert est la transformée de Laplace de la réponse impulsionnelle d'un système linéaire lorsque ses conditions initiales (ou aux limites) sont nulles. Elle permet de transformer le produit de convolution en simple produit :
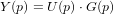
 Transformée de Laplace
Transformée de Laplace
Soit 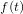 une fonction du temps. Sa transformée de Laplace unilatérale
une fonction du temps. Sa transformée de Laplace unilatérale 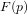 est
définie par
est
définie par 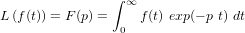 où
où 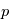 est la variable complexe.
est la variable complexe.
| f(t) | F(p) |
|---|---|
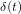 (Dirac) (Dirac) | 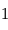 |
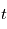 | 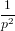 |
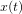 | 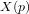 |
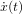 | 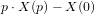 |
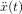 | 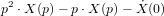 |
Soit l'équation 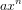
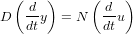 où
où 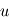 et
et 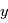 sont respectivement l'entrée et la sortie et
sont respectivement l'entrée et la sortie et 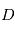 et
et 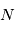 sont des polynômes à coefficients réels en (d/dt). Si l'on considère que les conditions initiales sont nulles, on peut réécrire l'équation différentielle précédente pour obtenir la fonction de transfert H :
sont des polynômes à coefficients réels en (d/dt). Si l'on considère que les conditions initiales sont nulles, on peut réécrire l'équation différentielle précédente pour obtenir la fonction de transfert H :
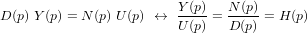
Les pôles d'une fonction de transfert sont les valeurs pour lesquelles le dénominateur D, aussi appelé équation caractéristique, s'annule. Attention, tout ceci est vrai à condition que la fonction de transfert soit sous forme irréductible. Pour que le système soit stable, il faut que tous les pôles soient strictement à l'intérieur du cercle unité (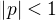 ).
).
Représentation de la boucle de contrôle d'attitude
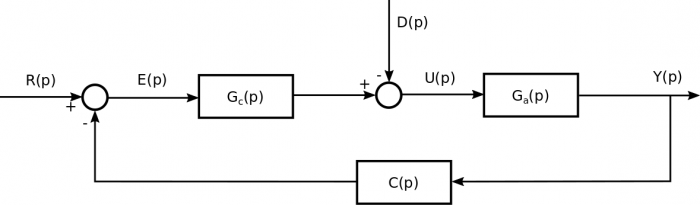
On représente la boucle du SCA comme un contrôle en boucle fermée, avec le terme de rétroaction. On note R(p) le signal de référence, Y(p) le signal de sortie, D(p) la perturbation, U(p) le signal de contrôle, Gc(p) le contrôleur, E(p) l'erreur, Gp(p) le matériel à contrôler et C(p) la dynamique des capteurs. Si l'on considère que les perturbations sont nulles, la fonction de transfert s'écrit :
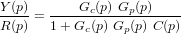
Le dénominateur de cette équation est un polynome dont les racines déterminent le type de réponse. Le contrôleur peut être utilisé pour stabiliser le système ou lui donner des caractéristiques particulières.
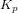
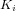
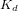
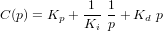
![[I] \ \ddot \theta (t) = u(t) + w(t)](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation30.png)
![[I]](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation31.png) est la matrice d'inertie,
est la matrice d'inertie, 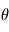 est l'angle,
est l'angle, 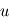 est le couple de contrôle et
est le couple de contrôle et 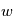 est le couple perturbateur extérieur.
est le couple perturbateur extérieur.
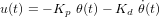
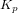 et
et 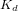 sont des gains qu'il faut déterminer. Le système en boucle fermée et son équation caractéristique s'écrivent alors :
sont des gains qu'il faut déterminer. Le système en boucle fermée et son équation caractéristique s'écrivent alors :
![[I] \ \ddot \theta (t) + [K_d] \ \dot \theta (t) + [K_p] \ \theta(t) = w(t) \ \leftrightarrow \ I \ p^2 + [K_d] \ p + [K_p] = 0](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation38.png)
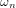 et
et 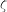 , respectivement la fréquence propre (fréquence de la réponse sinusoïdale du système non amorti) et le facteur d'amortissement. L'équation caractéristique est réécrite en introduisant ces deux nouvelles grandeurs :
, respectivement la fréquence propre (fréquence de la réponse sinusoïdale du système non amorti) et le facteur d'amortissement. L'équation caractéristique est réécrite en introduisant ces deux nouvelles grandeurs :
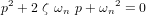
![[K_p] = [I] \ {\omega_n}^2](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation42.png) et
et ![[K_d] = 2 \ [I] \ \zeta \ \omega_n](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation43.png) . On choisit généralement le
. On choisit généralement le 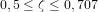 . Il est important de noter que l'information sur la dérivée provient de
. Il est important de noter que l'information sur la dérivée provient de 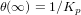 . Idéalement nous souhaitons que l'attitude en régime permanent soit nulle, c'est la raison pour laquelle nous introduisons le contrôleur PID (proportionnel-intégral-dérivé) :
. Idéalement nous souhaitons que l'attitude en régime permanent soit nulle, c'est la raison pour laquelle nous introduisons le contrôleur PID (proportionnel-intégral-dérivé) :
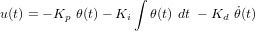
![[I] \ p^3 + [K_d] \ p^2 + [K_p] \ p + [K_i] = 0 \ \leftrightarrow \ \left( p^2 + 2 \ \zeta \ \omega_n \ p + {\omega_n}^2 \right) \left( p + \frac{1}{T} \right) = 0](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation47.png)
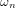 et
et 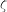 sont toujours la fréquence propre et le facteur d'amortissement, et
sont toujours la fréquence propre et le facteur d'amortissement, et 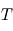 est la constante temporelle associée au contrôle intégral. Les gains du contrôleur PID s'expriment :
est la constante temporelle associée au contrôle intégral. Les gains du contrôleur PID s'expriment : ![[K_p] = [I] \left( {\omega_n}^2 + \frac{2 \ \zeta \ \omega_n}{T} \right)](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation51.png) ,
, ![[K_i] = [I] \ \frac{{\omega_n}^2}{T}](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation52.png) et
et ![[K_d] = [I] \left( 2 \ \zeta \ \omega_n + \frac{1}{T}\right)](../pages_nanosats/equations_nanosats-comprendre-techniques-lois-de-controle/equation53.png) . On choisit souvent la constante
. On choisit souvent la constante 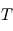 telle que :
telle que : 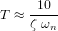 .
.