Transits d'exoplanètes
Auteurs: Emmanuel Lellouch, Jean-Mathias Griessmeier, Quentin Kral
- Décrire
- Définitions
- Différents mots pour une variété de phénomènes
- Dans le système solaire
- Hors du système solaire
- Des phénomènes riches d'enseignements
- Paramètres planétaires accessibles
- Paramètres planétaires
- Taille de la planète
- Orbite : Période et excentricité
- Orbite : Orientation
- Orbites perturbées
- Un système extraordinaire : TRAPPIST-1
- Atmosphère: composition et dynamique - I
- Atmosphère: composition et dynamique - II
- Atmosphère: composition et dynamique - III
- Atmosphère: composition et dynamique - IV
- Environnement planétaire accessible
- Transit de satellites
- Transit de comètes
- Transit d'anneaux
- Comprendre
- Des événements rares
- Probabilité de transit
- Recherche au hasard
- Temps des transits
- Géometrie détaillée d'un transit
- Durée du transit
- Mise en oeuvre de la méthode
- Différents objectifs scientifiques
- Equipement
- Difficultés de la méthode
- Variabilité stellaire
- Faux positifs
- Débusquer les faux positifs
- Complémentarité des méthodes
- Limites de la méthode des transits
- Complémentarité des méthodes de transit et de vélocimétrie
- Importance des données stellaire
- Spectroscopie des transits et courbes de phase
- Spectroscopie du transit
- Spectroscopie de l'éclipse secondaire
- Emission thermique de la planète
- Comment résoudre l'équation de transfert radiatif
- Courbes de phase
- Les missions Corot et Kepler et leurs résultats
- Deux missions de photométrie de haute précision
- Corot
- Kepler
- Se tester
- Projet
- Projet : Découverte de WASP-80
- WAST-80 : Les données
- WASP-80 : Les transits
- WASP-80 : La planète
- WASP-80 : Pour aller plus loin
-
Transits d'exoplanètes
Ce chapitre présente la recherche et l'étude des exoplanètes par la méthode des transits. Il décrit les techniques d'observation, ainsi que les phénomènes observés et les paramètres déduits de ces observations concernant la planète, son environnement, sa structure interne et son atmosphère.
La lecture de ce cours demande quelques connaissances sur les atmopshères planétaires disponibles ici.
Décrire
Auteur: Emmanuel Lellouch
Définitions
Différents mots pour une variété de phénomènes
Vus depuis la Terre, les objets célestes peuvent passer les uns devant les autres, ce qui conduit à l’obscuration partielle ou totale de l'objet le plus lointain. Lorsque deux objets ont une taille apparente différente, le passage du plus petit devant le plus grand est appelé transit . Celui du plus grand devant le plus petit est appelé occultation ou plus improprement éclipse .
Dans le système solaire
Jupiter
Phénomènes mutuels des satellites de Jupiter
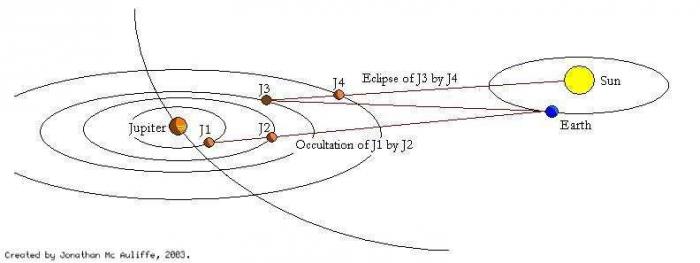
Dans le système solaire, les transits les plus courants sont ceux des satellites galiléens devant Jupiter, ainsi que leurs transits, occultations et éclipses mutuels. Dans le cas de Jupiter, lorsque la planète est proche de son équinoxe (tous les 5.5 ans environ), on peut observer les phénomènes mutuels de ses satellites galiléens, parmi lesquels on distingue entre transits, occultations et éclipses.
Mercure et Vénus
Transit de Vénus

Transit de Vénus de 2012 observé dans une bande H alpha, qui montre les tâches solaires et le filaments.
Crédit :
C. Hetlage,
APOD
Moins fréquents mais plus connus sont les transits de Mercure (13 ou 14 fois par siècle) et Vénus (2 fois, séparées de 8 ans, tous les 243 ans) devant le Soleil.
Le Soleil et la Lune
En principe, le terme éclipse (littéralement : privation de lumière) devrait être réservé aux situations dans lesquelles un corps passe dans l’ombre d’un autre et non derrière lui. Il est ainsi employé correctement lorsqu’on parle d’une éclipse de Lune – la Lune passant dans l’ombre de la Terre – mais improprement lorsqu’on parle d’une éclipse de Soleil, ce phénomène devant en toute rigueur être appelé occultation du Soleil par la Lune .
Le système solaire extérieur
Les planètes et petits corps du système solaire extérieur, très peu lumineux, passent assez souvent devant des étoiles du fond de ciel plus brillantes qu'eux. Ces occultations d'étoiles, comme les "ombres chinoises" révèlent des informations inaccessibles autrement.
Quelques-uns des résultats obtenus grâce à ces phénomènes sont décrits ci-dessous.
Hors du système solaire
hst-hd209458.png
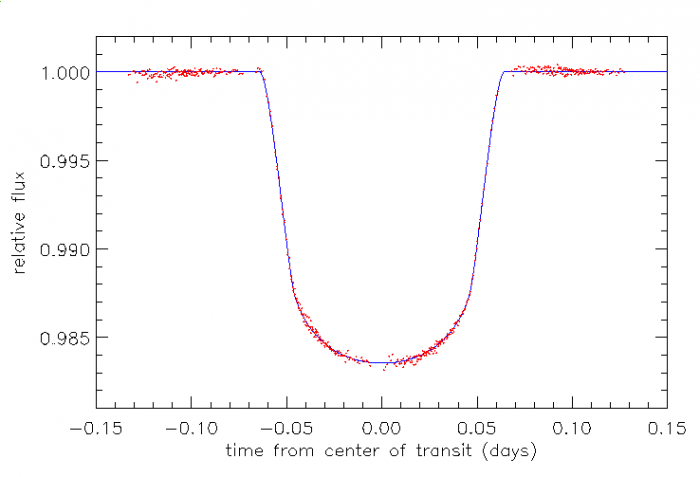
Transit de la planète HD 209458 b, observé par le Télecope Spatial
Crédit :
NASA
En sciences exoplanétaires, la méthode des transits consiste à mesurer les timings et l’ensemble des phénomènes observables lors du passage apparent d’une planète devant (figure ci-jointe- et derrière son étoile-hôte, lorsque ceux-ci se produisent en raison d’une orientation favorable de l’orbite planétaire (nous parlerons ci-après d’une planète transitante). Comme on le verra en détail, ces observations fournissent des informations irremplaçables sur la taille de la planète, ses caractéristiques orbitales, la structure et la composition de son atmosphère, voire la présence éventuelle de planètes supplémentaires dans le système.
Le passage de la planète derrière l’étoile (stricto sensu son occultation) est dans la littérature le plus souvent désigné par « transit secondaire » voire « éclipse secondaire », ou «anti-transit». Dans ce qui suit, on utilisera les termes transit (ou transit primaire) et éclipse secondaire pour le passage d’une planète devant et derrière l’étoile. L’observation de la planète hors transit, c’est-à dire dans la période de temps située entre le transit et l'éclipse secondaire fournit elle aussi des renseignements très intéressants sur la planète.
Des phénomènes riches d'enseignements
Roemer
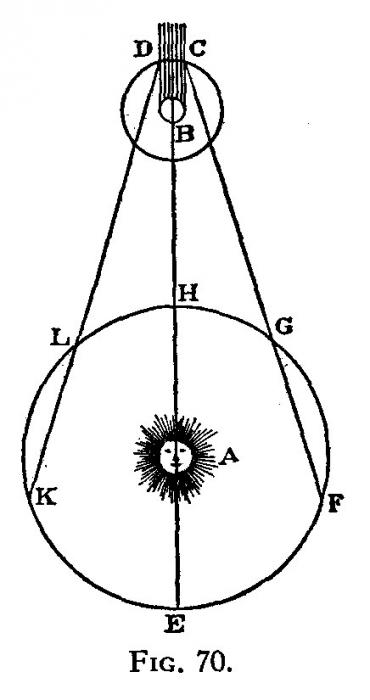
Gravure de l'article de Rømer dans le
JOURNAL DES SCAVANS de l'orbite de Io (en haut) observée de la Terre (en bas). L'article rapporte les 8 années d'observation et la conclusion que la lumière ne se propage pas instantanément.
Chariklo
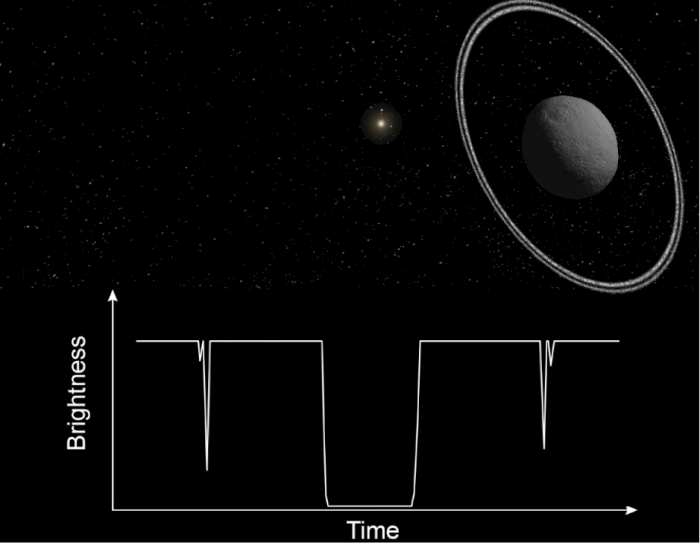
L'enregistrement du passage de l'astéroïde Chariklo devant une étoile a révélé la présente de deux anneaux.
Crédit :
L. Maquet
Dans différentes branches de l’astrophysique, l’observation de ces phénomènes de masquage ont donné historiquement des résultats scientifiques majeurs. Il y a exactement 400 ans, la mesure du timing des éclipses de Io par Jupiter a conduit le Danois Ole Rømer à la première estimation de la vitesse de la lumière (figure ci-jointe).
L’observation des transits de Vénus depuis différents points de la Terre a permis de calibrer les distances dans le système solaire (c’est-à-dire de mesurer l’unité astronomique) en employant la méthode des parallaxes. Elle a aussi fourni les premières indications sur la présence d’une atmosphère autour de Vénus (transit de 1761).
Les observations des éclipses de Soleil, qui permettent d’isoler la chromosphère, ont fourni de très nombreux résultats, parmi lesquels on se bornera à citer ici la découverte de l’hélium (1868), et la confirmation de la prédiction d’Einstein sur la déflection gravitationnelle de la lumière (1919) en comparant la distance apparente entre des étoiles selon que le Soleil était absent du champ ou présent (i.e. pendant une éclipse de Soleil).
Même si on se limite au système solaire, ces phénomènes continuent à fournir des informations majeures. La mesure des positions précises des satellites de Jupiter grâce aux phénomènes mutuels a permis de reconstituer leur mouvement orbital avec une précision suffisante pour en déduire le taux de dissipation d’énergie lié aux forces de marée dans l’intérieur de Io.
Dans des situations géométriquement semblables à celle des exoplanètes, la spectroscopie de Mercure et Vénus lors des transits récents devant le Soleil, et de Io en transit devant Jupiter, ont fourni de nouvelles information sur la composition et la structure de leurs atmosphères.
Un outil puissant d’étude des objets du système solaire lointain (objets trans-neptuniens) est fourni par la méthode de l’occultation stellaire : elle permet, par mesure du temps d’occultation – c’est-à-dire le temps de disparition de l’étoile derrière l’objet – la détermination de leur taille avec une précision (de l’ordre du kilomètre) inégalable par d’autres techniques. Les systèmes d'anneaux d'Uranus, de Neptune, du Centaure Chariklo (figure ci-jointe) et du transneptunien Haumea ont été découverts grâce à de telles occultations stellaires. Cette même technique permet de mesurer et de suivre l’évolution temporelle de la pression à la surface d’un objet comme Pluton.
Paramètres planétaires accessibles
Paramètres planétaires
L'observation des transits donne accès à des informations sur
Taille de la planète
Rayon
Géométrie des transits
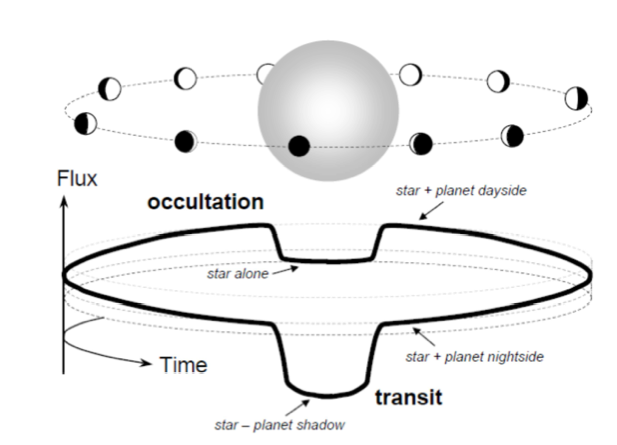
Figure 1 : Géométrie de l’orbite d’une planète transitante. Nous utilisons ici le terme éclipse secondaire pour désigner le passage de la planète derrière l’étoile, i.e. l’occultation.
Crédit :
A traduire
La figure ci-jointe montre schématiquement la géométrie d’observation d’une exoplanète transitante. L’observable la plus directe est la mesure de la variation de flux pendant le transit primaire et l'éclipse secondaire. Hors transit, le flux mesuré correspond à la somme du flux de l’étoile 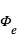 et celui de la planète
et celui de la planète 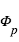 . Pendant l'éclipse secondaire, le flux mesuré est restreint à
. Pendant l'éclipse secondaire, le flux mesuré est restreint à 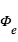 .
.
Pendant le transit primaire, une fois que la planète est entièrement devant le disque de l’étoile, une fraction de la surface de l'étoile est cachée, 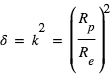 , où
, où 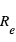 et
et 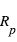 sont respectivement le rayon de l'étoile et de la planète. Le flux de lumière de l'étoile est réduit d'une fraction δ. Comme la planète est devant l’étoile, elle nous présente sa face non-éclairée, donc sa contribution au flux observé est nulle. En conséquence, le rapport du flux mesuré pendant le transit primaire à celui mesuré pendant l'éclipse secondaire (ou en pratique à celui mesuré à n’importe quel moment hors du transit) donne directement le rapport du rayon de la planète à celui de l’étoile.
sont respectivement le rayon de l'étoile et de la planète. Le flux de lumière de l'étoile est réduit d'une fraction δ. Comme la planète est devant l’étoile, elle nous présente sa face non-éclairée, donc sa contribution au flux observé est nulle. En conséquence, le rapport du flux mesuré pendant le transit primaire à celui mesuré pendant l'éclipse secondaire (ou en pratique à celui mesuré à n’importe quel moment hors du transit) donne directement le rapport du rayon de la planète à celui de l’étoile.
 Transit de planètes du système solaire
Transit de planètes du système solaire
Question 1)
Calculez la baisse de luminosité du Soleil dû à un transit de Jupiter, de la Terre.
Les petites étoiles favorisent la détection de transits
L'exercice ci-dessus montre que le transit de Jupiter devant le Soleil conduit à une baisse de luminosité de celui-ci de 1.05%. Pour la Terre passant devant le Soleil, l’assombrissement relatif n’est que de 0.0084%.
La perte de flux mesurée pendant l'éclipse secondaire dépend elle non seulement du rapport 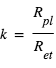 , mais également du rapport de l’intensité lumineuse spécifique (i.e. pour une surface donnée) émise par les deux objets. Comme on le verra plus loin, il dépend de de la longueur d’onde, et selon celle-ci, des températures de la planète et de l’étoile, ou de l’albédo de la planète.
, mais également du rapport de l’intensité lumineuse spécifique (i.e. pour une surface donnée) émise par les deux objets. Comme on le verra plus loin, il dépend de de la longueur d’onde, et selon celle-ci, des températures de la planète et de l’étoile, ou de l’albédo de la planète.
L’expression de la perte de flux au moment du transit montre que la détection d’un transit d’une exoplanète de rayon donné autour d’une étoile naine (de type M) est plus favorable qu’autour d’une étoile de type solaire ou d’une étoile géante. Par exemple, l’étoile Kepler- 42 a un rayon égal à 0.17 rayon solaire (120 000 km). Elle abrite 3 planètes, dont la plus petite (Kepler-42 d), a un rayon de ∼0.57 rayon terrestre, ce qui donne un signal photométrique de l’ordre de 0.1%, plus de dix fois plus fort que la Terre devant le Soleil.
Orbite : Période et excentricité
La grande puissance de la méthode des transits résulte de la reproductibilité du phénomène. Un système transitant peut être observé autant de fois que l’on souhaite, avec à chaque fois les mêmes caractéristiques en termes de timing et de profondeur de transit, ce qui permet l’accumulation de la précision sur ces deux paramètres. La précision sur la mesure des instants de transits est riche d’enseignements.
Dans le cas d’une orbite circulaire de période P, un transit et l'éclipse secondaire adjacente sont séparés temporellement de P/2. Ce n’est plus le cas pour une orbite elliptique, et la mesure de ces séparations temporelles (transit-éclipse et éclipse-transit) donne une information sur l’excentricité de l’orbite; plus précisément, elle contraint le produit e cos (ω), où e est l’excentricité et ω l’argument du périastre.
La mesure des durées relatives du transit et de l'éclipse secondaire fournissent aussi des contraintes sur ces paramètres, mais avec moins de précision, eu égard à la courte durée des transits par rapport à leur périodicité.
Au-delà même de la caractérisation statistique des orbites planétaires, l’intérêt physique de ces mesures d’excentricité est grand. Ainsi, pour les planètes proches de leur étoile, les effets de marée associés aux orbites elliptiques produisent un chauffage interne qu’il est possible d’estimer, fournissant des contraintes sur la structure thermique des objets.
Par ailleurs, s’agissant de la connaissance de la période orbitale et des instants de transit et d’éclipse, la méthode des transits est presque toujours plus précise que la méthode des vitesses radiales. Pour autant, ces paramètres interviennent dans l’interprétation des courbes de vitesse radiale (ce sont 3 des 6 paramètres libres associés à cette méthode), donc leur connaissance indépendante via les transits a un grand intérêt pour l’amélioration de la précision sur les autres.
Orbite : Orientation
Orientation de l'orbite
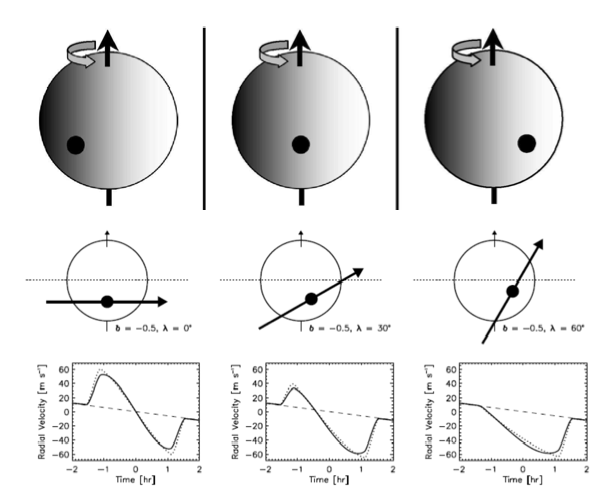
Figure 2 : Transit d’une exoplanète en présence de rotation stellaire. La planète masque d’abord des régions émettant vers le bleu, puis vers le rouge. La dernière ligne montre l’évolution de la vitesse radiale mesurée pour l’étoile pour différentes orientations de l’orbite planétaire. Dans les trois situations montrées, la durée du transit est la même de sorte que la simple observation photométrique du transit ne pourrait les distinguer.
Crédit :
A traduire
Une exoplanète qui transite devant son étoile possède une orientation favorable pour la spectroscopie des vitesses radiales : L'étoile et la planète tournent autour de leur centre de gravité. Au moment du transit planétaire, l'étoile est à son point le plus éloigné de la Terre (i.e. l'observateur) et sa vitesse Doppler s'annule.
S’y rajoute un effet subtil : en raison de sa rotation propre, le rayonnement d’une partie de l’étoile est décalé vers le bleu, l’autre vers le rouge (Fig. 2). Si la planète a une orbite prograde (dans le même sens que la rotation stellaire), elle masque d’abord des régions de l’étoile émettant un rayonnement décalé vers le bleu (zones grisées sur la Fig. 2), puis vers le rouge (zones claires). En conséquence, par rapport à sa valeur mesurée au centre du transit, la vitesse radiale globale de l’étoile est d’abord décalée vers le rouge, puis vers le bleu. C’est ce que l’on appelle l’effet Rossiter- McLaughlin. L’effet est loin d’être faible: en raison des fortes vitesses de rotation stellaires (typiquement 2 km/s pour le Soleil), il peut se chiffrer en quelques dizaines de mètre par seconde – soit souvent plus que la vitesse Doppler de l’étoile liée à la planète.
L’évolution du décalage Doppler de l’étoile pendant le transit permet alors non seulement de confirmer l’existence du transit, mais aussi de déterminer l’orientation de l’orbite planétaire, à savoir l’angle entre le plan orbital et l’axe de rotation de l’étoile (angle appelé obliquité de l’étoile).
Cette méthode a mis en évidence de nombreux cas de tels désalignements spin-orbite, voire d’orbites planétaires rétrogrades. L’origine de ces désalignements reste mal comprise, mais est sans doute liée à des phénomènes d’interaction, magnétique entre la jeune étoile et le disque proto-stellaire, ou gravitationnelle avec des compagnons stellaires au moment de la formation, qui auraient pu faire « basculer » l’axe de rotation stellaire. Une autre hypothèse serait que l’axe de rotation de l’étoile représente bien la direction perpendiculaire au plan du disque primordial, et que c’est le système planétaire dont le plan orbital a changé depuis sa formation.
Orbites perturbées
Orbites non kepleriennes et planètes additionnelles
TTV
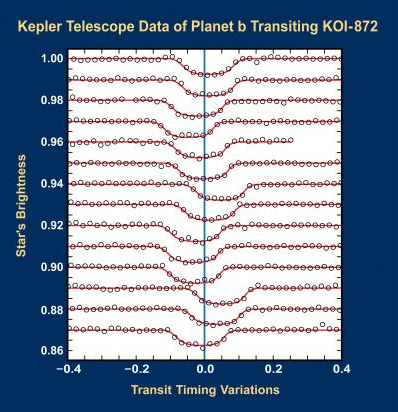
TTV de l'étoile KOI 872 (Kepler-46)
Crédit :
D. Forgan
Kepler-88

La planète Kepler-88b transite devant l'étoile Kepler-88. La planète Kepler-88c a été décourverte par les perturbations induites sur les instants des transits.
Crédit :
A. Santerne
De manière encore plus fine, la précision extraordinaire qui peut être atteinte sur les instants de transits peut révéler des cas d’orbites non-képleriennes. Ces situations peuvent résulter d’effets relativistes, de forces de marée liées à l’étoile, ou de perturbations associées à des forces gravitationnelles dues à des objets supplémentaires dans le système (deuxième étoile, planète additionnelle, etc.). Elles se manifestent par des variations sur les timings des transits primaire et secondaire, soit sur le long terme, ce qui peut indiquer une précession de l’orbite, soit à plus court terme, dans le cas de perturbations par des planètes non nécessairement transitantes dans le système.
Les planètes sur des orbites résonantes, c’est-à-dire présentant des commensurabilités de leurs périodes – produisent des variations particulièrement grandes des instants des temps de transit (figure ci-jointe). Cette effet est appelé TTV (transit time variation). L’ « inversion » des données de TTV en termes de propriétés (masse et orbite) des planètes perturbatrices est souvent « dégénérée » (i.e. n’a pas de solution unique), mais dans certains cas, une solution non-ambigüe peut être obtenue. Le plus souvent, l’ordre de grandeur des TTV est une très faible fraction de la période orbitale.
Un cas remarquable est celui de l’exoplanète Kepler-88b, une planète de 9 masses terrestres, qui présente des TTV de 12h d’amplitude, pour une période orbitale de 11 jours. Il a été prédit qu’ils étaient causés par une planète perturbatrice non-transitante de 0.7 masses de Jupiter, qui est ensuite été détectée par vélocimétrie radiale !
Un système extraordinaire : TRAPPIST-1
Transit triple de planètes de TRAPPIST-1
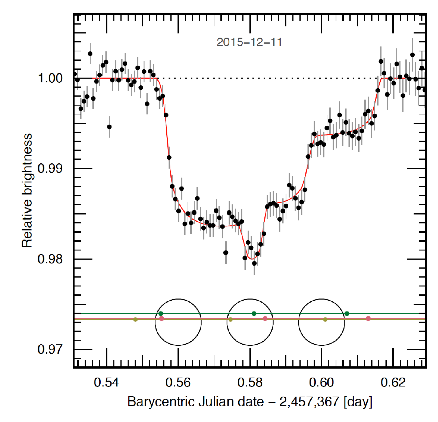
Courbe de lumière pour un transit triple des planètes TRAPPIST-1c, TRAPPIST-1e, et TRAPPIST-1f. La configuration des planètes (jaune, rouge, vert) à trois instants particuliers est indiquée en bas.
Crédit :
Gillon et al. 2017.
TRAPPIST-1 versus Jupiter
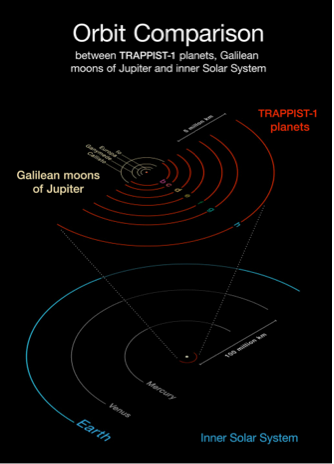
Taille comparée du système de 7 planètes TRAPPIST-1 avec le système des lunes galiléennes de Jupiter et le système solaire interne.
Crédit :
tréduire
Tout récemment (22 février 2017), un système exceptionnel de 7 planètes, toutes transitantes, a été découvert autour d’une étoile naine (rayon = 0.11 rayons solaires, masse= 0.08 masses solaires) ultra-froide (2550 K) appelée TRAPPIST-1 et située à 40 années-lumière. Les périodes orbitales (de 1.5 à 20 jours) sont telles que plusieurs de ces planètes peuvent transiter en même temps, et même s’occulter mutuellement pendant le transit, ce qui conduit à des courbes lumières d’une superbe complexité (Fig. ci-jointe).
Les tailles (Rp = 0.75 à 1.1 rayons terrestres) et masses (0.85 à 1.38 masses terrestres, mesurées par la méthode des TTV) indiquent clairement des planètes telluriques et trois d’entre elles pourraient avoir une température compatible avec l’eau liquide. Le système dans son ensemble (0.063 UA pour la planète la plus externe) tiendrait aisément dans l’orbite de Mercure, et apparaît comme un cas intermédiaire entre le système des satellites galiléens de Jupiter et celui du système solaire interne (Fig. ci-jointe).
Atmosphère: composition et dynamique - I
Structure verticale - transit primaire
Dans ce qui précède, nous n’avons parlé de d’observations photométriques des transits – c’est-à-dire dans une seule bande de longueur d’onde (outre la description de l’effet Rossiter-McLaughlin). Par ailleurs, nous avons implicitement supposé que la planète a un « bord net », de sorte qu’on pouvait parler de son « rayon » sans ambiguÏté. La réalité est plus floue. Les planètes géantes n’ont pas de surface solide bien définie, et même une planète tellurique peut posséder une atmosphère, qui influence la manière dont la lumière stellaire est absorbée pendant le transit. Concrètement, l’absorption préférentielle de la lumière à certaines longueurs d’onde par les gaz et/ou aérosols/nuages rend le « rayon d’absorption » de la planète plus grand à ces longueurs d’onde. Du coup, la mesure spectroscopique du transit, c’est-à-dire la variation de la profondeur d’absorption du transit en fonction de la longueur d’onde, permet d’obtenir des informations sur la composition de l’atmosphère, voire sa dynamique. Nous verrons plus loin les équations générales régissant ces principes. Notons que cette spectroscopie de transmission peut être effectuée dans tout l’infrarouge et jusqu’à l’ultraviolet, ce qui permet en principe de sonder une vaste gamme verticale de niveaux dans l’atmosphère, allant des troposphères (pression de plusieurs bars) jusqu’aux thermosphères/exosphères (nanobar).
Atmosphère: composition et dynamique - II
Structure verticale-transit secondaire
De même, il est extrêmement intéressant d’observer par spectroscopie l'éclipse secondaire. Comme on l’a vu, la différence entre le flux mesuré juste avant ou après le passage de la planète derrière l’étoile et celui mesuré pendant l'éclipse secondaire donne le rayonnement provenant de la planète elle-même (pour être précis, du côté éclairé de la planète). Selon le domaine de longueur d’onde, ce rayonnement planétaire peut-être de nature stellaire réfléchie ou thermique.
La première composante, qui domine dans le visible et le proche infrarouge, correspond à la lumière de l’étoile réfléchie par la planète. Le rayon étant approximativement connu par l’observation du transit, l’intensité de ce rayonnement réfléchi fournit l’albédo de la planète. Ce dernier résulte de la compétition entre les propriétés réfléchissantes/diffusantes et absorbantes de l’atmosphère (voire de sa surface). Pour une planète avec une atmosphère épaisse, les variations spectrales de l’albédo sont dues aux variations de ses propriétés de diffusion (par les gaz et/ou les nuages atmosphériques) avec la longueur d’onde, mais peuvent aussi faire intervenir la composition gazeuse (des espèces atomiques comme le sodium ou le potassium ont des raies d’absorption très fortes dans le visible). Comme on verra, la grande difficulté de la mise en œuvre de cette technique résulte dans la très faible intensité du signal planétaire à extraire.
Le domaine thermique, lui, correspond au rayonnement propre de l’atmosphère de la planète. Celui-ci dépend à la fois de la structure thermique verticale (la variation de la température avec la pression dans l’atmosphère de la planète) et des profils verticaux d’abondance des gaz – qui définissent le profil vertical de l’opacité atmosphérique. En termes de composition atmosphérique, la mesure du spectre thermique apparaît donc complémentaire de celle du spectre en transmission mesuré pendant le transit. Cette complémentarité reflète notamment le fait que les deux méthodes ne sondent pas les mêmes régions atmosphériques : le transit est sensible à la composition du limbe de la planète – i.e. les régions où la lumière stellaire est rasante (« terminateurs ») alors que l’émission thermique sonde le côté jour de la planète.
Par ailleurs, à une longueur d'onde donnée, le transit sonde des régions plus ténues de l'atmosphère que l'émission thermique.
Atmosphère: composition et dynamique - III
Chimie de l'atmosphère
A ce jour (janvier 2017), la spectroscopie des transits a permis de détecter un petit nombre d’espèces chimiques dans certaines exoplanètes (~20 objets en tout), parmi lesquelles les molécules H2O, CO2, CO, CH4, et les espèces atomiques H, C, O, Na, K. De manière très générale, l’intérêt de ces mesures est double, permettant (i) d’en déduire la composition élémentaire (par exemple le rapport C/O), qui donne des contraintes sur les processus de formation de ces objets (ii) de caractériser les processus physiques (photochimie, condensation, thermochimie à l’équilibre ou hors-équilibre, transport vertical, échappement atmosphérique...) qui gouvernent les atmosphères. L’étude des spectres exoplanétaires renseigne aussi sur la présence de nuages dans leurs atmosphères, dans la mesure où des nuages diffusants ou absorbants à haute altitude masquent les absorptions moléculaires attendues.
Atmosphère: composition et dynamique - IV
Courbe de phase
Transits et courbe de phase de HD189733 b
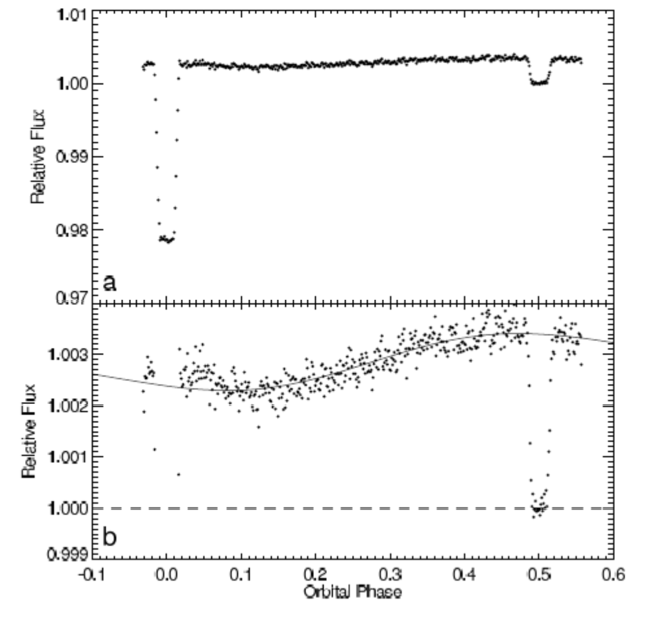
Figure 3 : Transit, éclipse secondaire, et courbe de phase de la planète HD 189733 b, observés à une longueur d’onde de 8
μm avec le télescope spatial infrarouge Spitzer. Les courbes sont normalisées au flux stellaire (1.000 pendant l'éclipse secondaire).
Le transit (à la phase 0.0) fait environ 2.1% de profondeur, ce qui indique un rapport des rayons
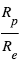
de 1.0%. L'éclipse secondaire (phase 0.5) indique que le côté jour de la planète émet 0.3% du rayonnement stellaire à cette longueur d’onde, impliquant une température d’environ 1210 K. La figure du bas (zoom vertical de celle du haut) montre la courbe de phase. Après modélisation, celle-ci indique que la température du côté nuit est d’environ 970 K, « seulement » 240 K plus froid que sur le côté jour, ce qui implique une forte redistribution de la chaleur par la dynamique atmosphérique. D’après Knutson et al. 2007.
Crédit :
à traduire
La figure montre qu’au cours de sa révolution autour de l’étoile, une exoplanète présente différentes phases : côté nuit au moment du transit, côté jour juste avant/après l'éclipse secondaire, et à l’instar de la Lune, des phases de croissant/quartier tout au long de l’orbite.
Le suivi de l’émission thermique avec la position de la planète sur son orbite – et ceci est vrai même pour une planète ne transitant pas – permet ainsi de mesurer les variations spatiales – en l’occurrence les variations avec l’heure locale pour une orbite circulaire – des propriétés atmosphériques. Ces courbes de phase renseignent principalement sur la variabilité diurne des températures atmosphériques. Par exemple, on pourrait s’attendre à ce que les Jupiter chauds, qui, dus aux effets de marée, sont en rotation synchrone autour de leur étoile, présentent des écarts de températures gigantesques entre les côtés éclairé et sombre. Ce n’est en fait souvent pas le cas (voir exemple sur la figure ci-jointe), ce qui implique une forte redistribution de la chaleur par des vents atmosphériques. Il est également généralement observé que le maximum de température ne se produit pas au midi local, mais est décalé vers les zones « de l’après-midi », ce qui s’explique par des effets d’inertie thermique.
Une méthode complémentaire consiste à résoudre temporellement l'éclipse secondaire dans le domaine thermique : la disparition progressive derrière l’étoile de la planète permet de déterminer successivement les températures de « tranches de planète » correspondant à des heures locales différentes, et ainsi d’établir une carte de températures.
La spectroscopie des transits donne enfin potentiellement un accès direct à la vitesse des vents atmosphériques. En effet si une molécule est détectée par spectroscopie du transit, la mesure précise de la longueur d’onde des raies planétaires peut éventuellement indiquer des décalages spectraux diagnostics de vitesses de vent. Ainsi, un décalage vers le bleu des raies de CO dans le cas de HD209458b a été interprété comme la signature de vents jour-nuit de l’ordre de 2 km/s. Des complications liées à la connaissance précise de l’orbite de la planète peuvent toutefois survenir. Dans un cas, il a aussi été possible de mesurer la période de rotation propre d’une exoplanète (β-Pictoris b) à partir de la largeur des raies de CO.
Environnement planétaire accessible
Transit de satellites
Nous n’avons ci-dessus parlé que de transits de planètes devant des étoiles. Le phénomène peut être généralisé au transit d’autres objets de nature planétaires, tels que : satellites, astéroïdes/comètes, anneaux.
Un satellite d’une exoplanète transitante doit généralement lui-même transiter et peut donc en être détecté directement par une allure particulière des courbes ingress/egress. Même si le satellite est trop petit pour être observé directement, un autre effet potentiellement détectable serait la mesure de TTV, dues au fait que la position de la planète oscille autour du centre de masse planète-satellite. Les données de transit de la planète Kepler-1625 b ont montré la premiètre trace de présence d'un exo-satellite, appelé Kepler-1625 b I
Transit de comètes
En revanche, on connaît deux cas de systèmes exoplanétaires avec transits de comètes. Le plus célèbre et le premier découvert est celui du disque de débris de l’étoile β-Pictoris, dont le spectre présente des raies atomiques (Ca II par exemple) variables temporellement, qui sont interprétées comme la signature de comètes en évaporation passant devant l’étoile. L’analyse statistique de ces signatures prouve qu’il existe deux familles de comètes différant par leur type d’orbite. A noter que le système de β-Pictoris possède également une planète géante (β-Pictoris b), découverte par imagerie directe, d’environ 7 masses de Jupiter, de période 22 ans. La recherche de son éventuel transit n'a, pour le moment rien donné.
Des transits de comètes devant une étoile (transit par le noyau cométaire et pas signature spectrale du nuage comme dans le cas de β-Pictoris) ont été détectés par Kepler en 2017.
Transit d'anneaux
Transit d'anneaux
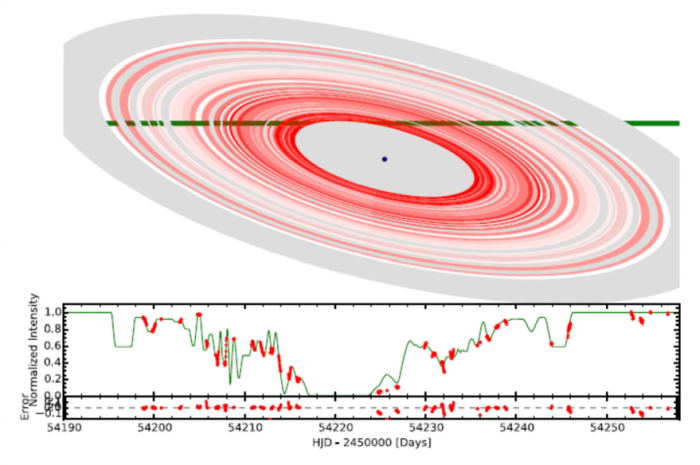
Figur 4 : Modèle et courbe de transit du système SWASP-J1407. La planète (point au centre) est détectée par vitesse radiale mais ne transite pas. Elle est en revanche entourée d’anneaux géants qui transitent devant l’étoile en 56 jours. La bande verte indique le parcours de l’étoile relatif aux anneaux pendant le transit. Les anneaux présentent un « vide » aux 2/3 environ de leur extension, ce qui pourrait indiquer l’existence d’une lune.
Crédit :
à traduire
Enfin, on a découvert le cas exceptionnel d’une exoplanète qui semble entourée d’anneaux (1SWASP J1407 b ; compte tenu de sa masse, environ 20 masses de Jupiter, il pourrait s’agir d’une naine brune). Ces anneaux, dont l’existence est attestée par leur transit devant l’étoile (Fig. 4), constituent un système géant (rayon ~90 millions de km, soit 200 fois les anneaux de Saturne) et pourraient abriter une masse totale d’environ 1 masse terrestre. Un modèle invoquant 37 anneaux distincts permet de reproduire la courbe du transit, qui dure 56 jours. A noter que le modèle présente une zone vide d’anneaux à environ les 2/3 du rayon total, peut-être la conséquence d’une lune de ~1 masse terrestre.
Comprendre
Auteur: E. Lellouch
Des événements rares
Probabilité de transit
Recherche au hasard
 Détectabilité des planètes par transit
Détectabilité des planètes par transit
Quelle est la probabilité, pour un extraterrestre, de détecter par transit,
Question 1)
- la Terre ? - Jupiter? - une planète à 0.05 UA d’une étoile de type solaire?
Le Soleil a un rayon de 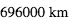 . L'orbite de la Terre a un rayon de
. L'orbite de la Terre a un rayon de 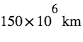 soit 1 U.A. (Unité Astronomique). L'orbite de Jupiter est à 5.2 U.A.
soit 1 U.A. (Unité Astronomique). L'orbite de Jupiter est à 5.2 U.A.
Cette probabilité peut se traduire en termes du nombre moyen d’étoiles qu’il faut observer pour espérer découvrir une exoplanète transitante à un rayon orbital donné. Si on note η la fraction des étoiles possédant une telle planète, ce nombre est de l’ordre de 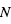 ∼
∼ 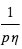 . Par exemple, les « Jupiters chauds » ont une distance type à leur étoile de 0.05 UA, et concernent environ 1 % des étoiles. Ceci donne p ∼0.1 et N ∼1000.
. Par exemple, les « Jupiters chauds » ont une distance type à leur étoile de 0.05 UA, et concernent environ 1 % des étoiles. Ceci donne p ∼0.1 et N ∼1000.
Même dans ce cas très favorable (planète proche), on voit que la recherche d’exoplanètes nouvelles par transit nécessite l’observation en aveugle de grands échantillons.
L'exercice ci-dessus montre que la probabilité de détecter la Terre par transit n'est que de 0.45%. Pour Jupiter, la probabilité est de 0.09%. En revanche, pour une planète à 0.05 UA autour d’une étoile de type solaire, la probabilité atteint 9 %. Les probabilités de transit et d'éclipse secondaire peuvent différer lorsque l’orbite planétaire est d’excentricité non-nulle (elliptique) de sorte qu’il est en principe possible d’observer un transit primaire sans transit secondaire et vice-versa.
Temps des transits
Géometrie détaillée d'un transit
Temps
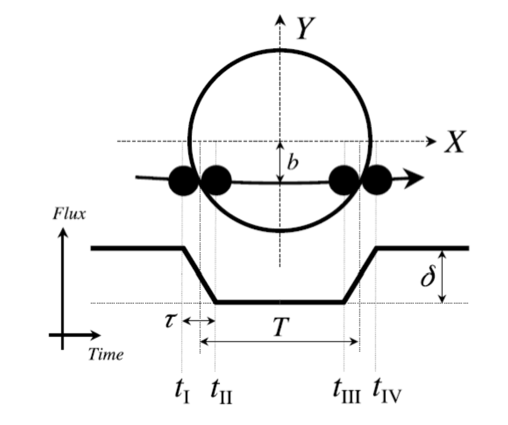
Figure 5 : Géométrie d’un transit. δ est la profondeur du transit, b le paramètre d’impact, T la durée du transit et τ la durée de l’ingress.
Crédit :
à traduire
La géométrie d’un transit est représentée sur la Fig. 5.
Appelons 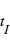 à
à 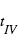 les 4 « temps de contact », c’est-à-dire les instants auxquels les disques de la planète et de l’étoile sont tangents. L’instant moyen de l’entrée (du disque planétaire devant le disque stellaire) est
les 4 « temps de contact », c’est-à-dire les instants auxquels les disques de la planète et de l’étoile sont tangents. L’instant moyen de l’entrée (du disque planétaire devant le disque stellaire) est 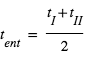 ; de même l’instant moyen de la sortie (du disque planétaire) est
; de même l’instant moyen de la sortie (du disque planétaire) est 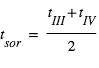 . L’intervalle de temps séparant ces deux instants, noté T, est par définition la « durée du transit », alors que
. L’intervalle de temps séparant ces deux instants, noté T, est par définition la « durée du transit », alors que 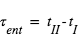 et
et 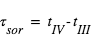 sont respectivement la durée de l’entrée et de la sortie. On note également b le « paramètre d’impact », i.e. la distance minimale – exprimée en fraction de rayon stellaire – entre la position apparente de la planète et le centre de l’étoile.
sont respectivement la durée de l’entrée et de la sortie. On note également b le « paramètre d’impact », i.e. la distance minimale – exprimée en fraction de rayon stellaire – entre la position apparente de la planète et le centre de l’étoile.
Durée du transit
Avec ces définitions, en se limitant au cas des orbites circulaires et en faisant les approximations raisonnables suivantes : 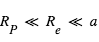 , et
, et 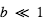 (transit non-rasant), on peut montrer que la durée du transit est égale à :
(transit non-rasant), on peut montrer que la durée du transit est égale à :
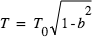 où
où 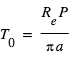 , P étant la période orbitale.
, P étant la période orbitale.
Par ailleurs, 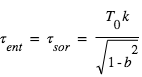 , où
, où 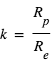 En combinant l’expression de
En combinant l’expression de 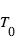 ci-dessus avec la 3eme loi de Kepler, et en se ramenant au cas du système solaire, on obtient
ci-dessus avec la 3eme loi de Kepler, et en se ramenant au cas du système solaire, on obtient 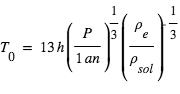 expression dans laquelle la seconde parenthèse représente le rapport de la densité de l’étoile à celle du Soleil. Ainsi, vu depuis une autre étoile, le transit de la Terre devant le Soleil ne dure que 13 h une fois tous les ans, et celui de Jupiter ne dure que 30 h une fois tous les douze ans, ce qui illustre à nouveau la rareté du phénomène. Bien évidemment, la mesure de la période requiert l’observation d’au moins deux transits.
expression dans laquelle la seconde parenthèse représente le rapport de la densité de l’étoile à celle du Soleil. Ainsi, vu depuis une autre étoile, le transit de la Terre devant le Soleil ne dure que 13 h une fois tous les ans, et celui de Jupiter ne dure que 30 h une fois tous les douze ans, ce qui illustre à nouveau la rareté du phénomène. Bien évidemment, la mesure de la période requiert l’observation d’au moins deux transits.
Mise en oeuvre de la méthode
Différents objectifs scientifiques
Les expressions ci-dessus montrent que les transits sont des événements a priori rares, puisque seule, une faible fraction des exoplanètes transitent, et parmi celles-ci, seulement pendant une faible fraction de leur période orbitale.
Il faut donc distinguer entre les différents objectifs suivants: (i) la recherche d’exoplanètes, qui comme on l’a vu nécessite l’observation de grands échantillons (ii) le suivi photométrique de systèmes planétaires découverts en vélocimétrie radiale pour voir s’ils donnent lieu à des transits (iii) la caractérisation d’exoplanètes transitantes, notamment par spectroscopie.
Equipement
De par sa simplicité, la méthode est en principe accessible avec un équipement modeste, puisqu’au premier ordre il s’agit simplement (sauf pour le troisième objectif) de suivre photométriquement une étoile qui peut être relativement brillante. De fait, le premier transit d’exoplanète (celui de HD209458b, dont l’étoile a une magnitude ∼ 8) fut observé depuis le sol, en 2000, à l’aide d’un simple télescope de 25 cm, doté d’une caméra CCD. De nombreux programmes de recherche de transits au sol ont été développés, tels que TrES, XO, HAT, SuperWASP, avec des télescopes de ∼10 cm qui font des relevés sur des étoiles de magnitude 10 à 12, ou OGLE, avec un télescope de 1 m pour des étoiles de magnitude 14-16. A ce jour (fin 2016), ces relevés depuis le sol ont permis de découvrir environ 250 exoplanètes, notamment avec SuperWASP et HAT.
Comme on l’a vu plus haut, le transit d'une planète géante (resp. tellurique) autour d’une étoile de type solaire produit typiquement un signal photométrique de 1 % (resp. 0.01 %). En raison de la turbulence atmosphérique, les planètes telluriques ne sont pas à la portée des observations au sol, sauf autour des étoiles naines. Ce problème est éliminé par l’emploi d’observations depuis l’espace, qui ont en outre l’avantage de s’affranchir des aléas de la météo et des interruptions jour-nuit. Dans tous les cas, l’extraction des signaux planétaires requiert des techniques élaborées de photométrie de haute précision, excluant au maximum les erreurs systématiques éventuelles. Les projets spatiaux CoRoT et Kepler et leurs résultats sont décrits ci-après.
Difficultés de la méthode
Variabilité stellaire
La description faite plus haut de la perte de flux pendant un transit suppose que le flux stellaire est indépendant de la position sur l’étoile et constant dans le temps. Dans la réalité, le rayonnement stellaire est généralement caractérisé par un assombrissement centre-bord, lié au fait que le rayonnement au limbe provient d’un niveau plus élevé, et par conséquent plus froid, dans l’atmosphère de l’étoile, que celui au centre. En conséquence, l’atténuation du rayonnement de l’étoile lors d’un transit planétaire n’est pas purement géométrique.
Aux longueurs d’onde où l’assombrissement centre-bord est important, les courbes de lumière apparaissent ainsi plus « piquées » (c’est-à-dire moins plates) près de leur centre, puisque la planète masque alors une zone de rayonnement plus intense.
De manière plus générale, les étoiles présentent des hétérogénéités locales de flux, associées notamment aux tâches stellaires liées à l’activité de l’étoile. Leur masquage pendant le transit peut conduire à des irrégularités dans le profil d’atténuation de l’étoile, ce qui compliquera la détermination du rayon planétaire. Ces problèmes sont particulièrement sérieux dans le cas des étoiles géantes et sous-géantes. L’activité stellaire, qui induit une variation temporelle du flux total émis par l’étoile, peut aussi conduire à des courbes de lumières non parfaitement reproductibles dans le temps.
Faux positifs
Faux positifs
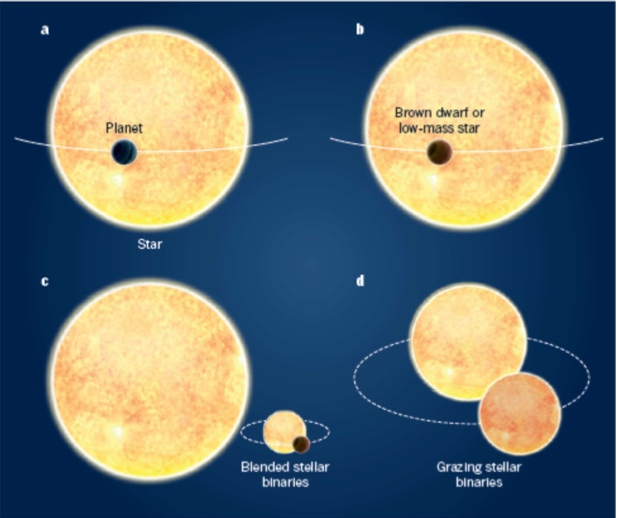
Figure 6 :Transit d’une exoplanète devant son étoile (a), et trois types de « faux positifs » : (b) Transit d’une naine brune ou d’une étoile de très faible masse (c) transit d’une binaire à éclipse en présence d’une étoile brillante dans un système triple (d) transit rasant d’une binaire à éclipse. Au premier ordre, toutes ces situations donnent des courbes de lumières semblables.
Crédit :
à traduire
Une faible atténuation temporaire et reproductible du flux stellaire peut sembler être la signature non-ambiguë d’un passage planétaire. Pourtant, il existe d’autres situations pouvant conduire au même type de signal (Fig. 6), telles que :
le transit rasant d’une étoile dans un système binaire à éclipses
le cas d’un système triple incluant une étoile brillante et une binaire à éclipses peu lumineuse : dans ce cas, l’effet du transit « normal » dans la binaire à éclipses est fortement dilué par la présence de l’étoile brillante, ce qui donne au phénomène l’apparence d’un transit planétaire de faible profondeur. Une variante de cette situation est le cas où la binaire à éclipse et l’étoile brillante ne font pas partie d’un système triple, mais se trouvent dans un alignement de circonstance.
Enfin, même dans les cas où on peut établir qu’il s’agit bien du transit d’un objet unique devant l’étoile étudiée, il faut encore prouver que l’objet en transit est bien une planète : en effet, les étoiles de faible masse (<10% de la masse du Soleil) et les naines brunes ont des rayons comparables à celles d’une planète géante comme Jupiter, et ne s’en distinguent que par leur masse bien plus élevée.
Débusquer les faux positifs
Il y a différentes manière de débusquer ces « faux positifs ». Ainsi les cas des transits rasants peuvent être identifiés par leur forme plus piquée (en « V ») que celle des transits planétaires (en « U »). Par ailleurs, comme on l’a vu plus haut, la durée du transit donne une mesure de la densité de l’étoile-hôte ; une solution aberrante (c’est-à-dire incohérente avec celle que l’on peut estimer à partir de la température de l’étoile) indiquera qu’il ne s’agit pas d’un transit planétaire. Enfin, pour distinguer entre une véritable planète et un objet sous-stellaire de même rayon, le seul moyen est de déterminer la masse de l’objet par vélocimétrie radiale. L’étude (et l’élimination) des faux positifs est fondamental pour les études statistiques de population planétaire. Ce taux s’avère important et fortement dépendant des types de planètes. Par exemple, dans le cas des données Kepler, il est de l’ordre de 10 à 20 % globalement, mais peut atteindre 35-55% pour les planètes géantes, plus difficiles à distinguer des étoiles de faible masse et naines brunes. En revanche, le taux de faux positifs dans le cas des systèmes multi-planétaires (en particulier dans le cas des systèmes à TTV, voir ci-dessus) est faible.
Complémentarité des méthodes
Limites de la méthode des transits
L’observation photométrique du transit ne fournit que le rapport du rayon de la planète à celui de l’étoile, pas le rayon absolu de la planète. Par ailleurs, sauf dans les cas où des perturbations gravitationnelles entrent en jeu (TTV), les transits en eux-mêmes ne contraignent pas les masses planétaires.
Complémentarité des méthodes de transit et de vélocimétrie
Importance des données stellaire
Densité des exoplanètes
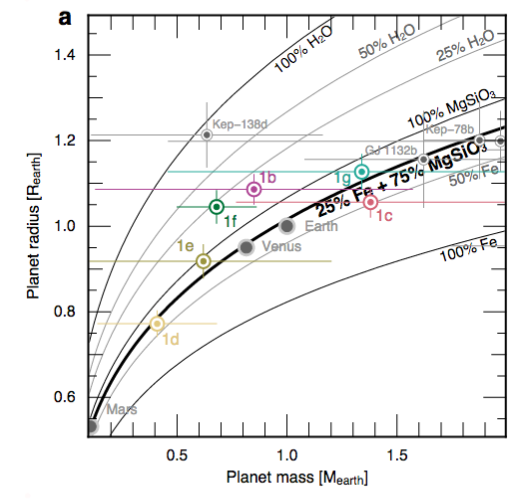
Diagramme masse-rayon des planètes TRAPPIST-1, comparées aux planètes telluriques du Système Solaire et quelques autres exoplanètes. Sont montrées aussi les courbes theoriques pour des planètes de différentes compositions
Crédit :
Gillon et al. 2017
A nouveau, une limitation est que 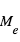 n’est pas connue. Il faut donc combiner les mesures de transit et de vitesse radiale avec des informations indépendantes sur l’étoile, typiquement obtenues via les modèles d’évolution stellaire, qui donnent des relations entre âge, luminosité, rayon, masse et composition.
n’est pas connue. Il faut donc combiner les mesures de transit et de vitesse radiale avec des informations indépendantes sur l’étoile, typiquement obtenues via les modèles d’évolution stellaire, qui donnent des relations entre âge, luminosité, rayon, masse et composition.
Par ailleurs, comme indiqué en 2.2, la profondeur du transit 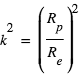 , la durée du transit T et la durée de l’ingress/egress contraignent le rapport
, la durée du transit T et la durée de l’ingress/egress contraignent le rapport 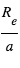 et le paramètre d’impact b, ce qui permet de « calibrer » le rayon planétaire en absolu. Si les propriétés stellaires sont suffisamment bien connues, on peut donc obtenir des valeurs absolues du rayon et de la masse planétaire, donc de sa densité, ce qui a évidemment une importance énorme pour contraindre la nature (gazeuse, glacée, rocheuse) et la structure interne de la planète.
et le paramètre d’impact b, ce qui permet de « calibrer » le rayon planétaire en absolu. Si les propriétés stellaires sont suffisamment bien connues, on peut donc obtenir des valeurs absolues du rayon et de la masse planétaire, donc de sa densité, ce qui a évidemment une importance énorme pour contraindre la nature (gazeuse, glacée, rocheuse) et la structure interne de la planète.
Finalement, en combinant la relation ci-dessous avec la 3e loi de Kepler, on peut déterminer la gravité planétaire 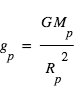 indépendamment des propriétés de l’étoile :
indépendamment des propriétés de l’étoile :
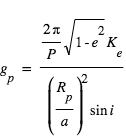 La connaissance de
La connaissance de 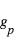 est nécessaire pour l’élaboration de modèles d’atmosphères.
est nécessaire pour l’élaboration de modèles d’atmosphères.
Spectroscopie des transits et courbes de phase
Spectroscopie du transit
Spectre en transmission de HD 209458 b
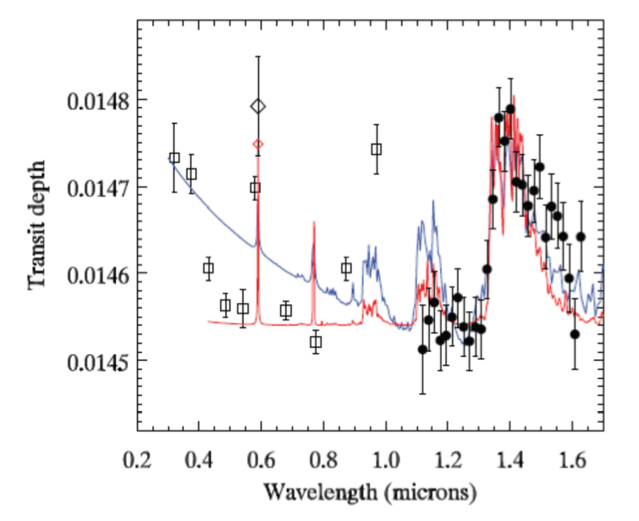
Figure 7 : Le spectre en transmission de HD 209458b, exprimé en termes de profondeur du transit. La partie visible (<1 micron) suggère l’effet de la diffusion Rayleigh et de l’absorption par le sodium à 0.58 micron. La présence de la vapeur d’eau est clairement visible à 1.4 microns (Deming et al. 2013).
Crédit :
à traduire
Comme exposé plus haut, le principe de la spectroscopie du transit est de mesurer des variations spectrales de la profondeur du transit comme diagnostic de composition atmosphérique. A une longueur d’onde où l’atmosphère absorbe, le rayon "effectif" de la planète est augmenté d’une quantité 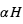 , où H est la hauteur d’échelle de l’atmosphère et α est généralement un nombre de l’ordre de quelques unités. La profondeur du transit δ est donc augmentée de :
, où H est la hauteur d’échelle de l’atmosphère et α est généralement un nombre de l’ordre de quelques unités. La profondeur du transit δ est donc augmentée de :
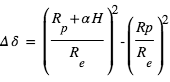 ∼
∼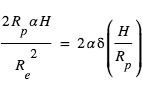
Cette relation montre fondamentalement que l’effet est d’autant plus grand que H est grande, i.e. que l’atmosphère est chaude, de faible masse moléculaire, et que la gravité est faible. Par exemple, pour un Jupiter chaud (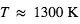 ,
, 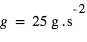 , masse moléculaire = 2 amu (
, masse moléculaire = 2 amu (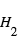 ),
), 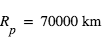 ), on obtient
), on obtient 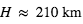 , ce qui fait
, ce qui fait 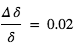 en adoptant
en adoptant 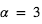 . Pour une "Terre" (
. Pour une "Terre" (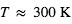 ,
, 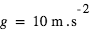 , masse moléculaire = 28 amu (
, masse moléculaire = 28 amu (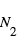 ),
), 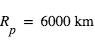 ), on trouve
), on trouve 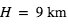 et
et 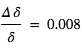 , en prenant toujours
, en prenant toujours 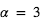 .
.
Dans les deux cas, l’ordre de grandeur est donc une augmentation relative de la profondeur du transit de l’ordre de 1% de sa valeur. Pour la planète tellurique, compte tenu que le transit géométrique est déjà inférieur à 0.01%, le signal spectral 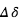 est donc inférieur à
est donc inférieur à 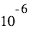 , ce qui illustre l’extrême difficulté de ce type de mesures.
, ce qui illustre l’extrême difficulté de ce type de mesures.
Echelle de hauteur
La spectroscopie du transit primaire permet d’estimer l’échelle de hauteur atmosphérique. Imaginons d’abord que le coefficient d’absorption intrinsèque de l’atmosphère varie avec la longueur d’onde λ, mais pas avec le niveau d’altitude dans l’atmosphère. Si on note 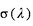 la section efficace d’absorption à la longueur d’onde λ, l’opacité en visée verticale est
la section efficace d’absorption à la longueur d’onde λ, l’opacité en visée verticale est
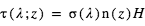 , où
, où 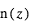 est la concentration de l’espèce absorbante à l’altitude z. Comme le transit sonde les couches au limbe, l’opacité le long de la ligne de visée est multipliée par le facteur géométrique d’augmentation du parcours
est la concentration de l’espèce absorbante à l’altitude z. Comme le transit sonde les couches au limbe, l’opacité le long de la ligne de visée est multipliée par le facteur géométrique d’augmentation du parcours 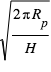 , et vaut donc :
, et vaut donc : 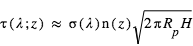 On peut montrer que le rayon planétaire effectif à la longueur d’onde λ est égal au rayon de la surface augmenté de la hauteur
On peut montrer que le rayon planétaire effectif à la longueur d’onde λ est égal au rayon de la surface augmenté de la hauteur 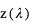 pour laquelle l’opacité en visée horizontale vaut environ 0.56 :
pour laquelle l’opacité en visée horizontale vaut environ 0.56 : 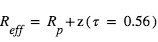 Comme
Comme 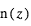 est relié à la concentration
est relié à la concentration 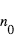 à la surface, selon
à la surface, selon 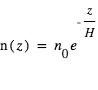 , on peut en déduire
, on peut en déduire
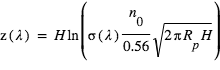 ce qui confirme que l’augmentation du rayon effectif est essentiellement proportionnelle à H (le terme dans le ln variant lentement avec H).
ce qui confirme que l’augmentation du rayon effectif est essentiellement proportionnelle à H (le terme dans le ln variant lentement avec H).
Cette expression montre que la variation du rayon effectif avec la longueur d’onde suit : 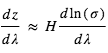 Si l’on connaît le mécanisme physique responsable de l’absorption (par exemple, la diffusion Rayleigh où σ varie comme une puissance de λ), la mesure de la variation du rayon effectif avec la longueur d’onde fournit directement la hauteur d’échelle de l’atmosphère
Si l’on connaît le mécanisme physique responsable de l’absorption (par exemple, la diffusion Rayleigh où σ varie comme une puissance de λ), la mesure de la variation du rayon effectif avec la longueur d’onde fournit directement la hauteur d’échelle de l’atmosphère 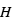 , donc une estimation de sa composition principale si la température peut être estimée indépendamment.
, donc une estimation de sa composition principale si la température peut être estimée indépendamment.
Le raisonnement précédent est valable en première approximation lorsque l’opacité atmosphérique est le fait des brumes, mais l’est moins pour une absorption par les gaz, car celle-ci dépend intrinsèquement fortement de la pression. Ce développement analytique doit donc être remplacé par des modèles numériques. Il n’en reste pas moins vrai que le spectre en transmission montre la planète « plus grosse » dans les bandes d’absorption gazeuse qu’en dehors de ces bandes, et qu’il est alors possible de contraindre la composition chimique (Fig. 7).
Les premières découvertes d’espèces chimiques dans les spectres d’exoplanètes en transmission datent des années 2002-2003 avec la détection d’espèces atomiques (Na, H, et plus tard K, C, O) dans le spectre visible. Le cas de l’hydrogène atomique est particulier car il donne lieu à des transits extrêmement profonds (15%), causés par des atmosphères d’hydrogène très étendues et en échappement rapide. Dans l’infrarouge, dû à la grande difficulté d’extraire les spectres, des controverses ont eu lieu sur la réalité et surtout la quantification des signatures spectrales en termes de paramètres atmosphériques. Il semble toutefois qu’un nombre important de ces spectres montrent les signatures spectrales de H2O, celles de CH4, CO2, et CO étant également présentes sur quelques objets. Une caractéristique très fréquente est le rôle des brumes ou nuages de haute altitude, qui contribuent à l’émission dans le spectre visible et tendent à masquer les signatures des gaz dans l’infrarouge.
Spectroscopie de l'éclipse secondaire
Comme on l’a vu plus haut, l’observation de l'éclipse secondaire permet en principe de déterminer par différence la quantité de radiation que nous envoie une exoplanètes, que ce soit sous forme de lumière stellaire réfléchie ou de rayonnement thermique propre. La difficulté est ici le contraste de luminosité entre la planète et l’étoile.
La profondeur de l'éclipse secondaire s'écrit :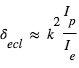 où
où 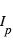 et
et 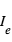 sont les intensités (par élément de surface) émises par la planète et l’étoile et
sont les intensités (par élément de surface) émises par la planète et l’étoile et 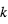 est le rapport des rayons
est le rapport des rayons 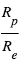 .
.
Dans la composante stellaire réfléchie, juste avant l'éclipse secondaire, la planète – qui présente alors sa face entièrement éclairée – reçoit une fraction
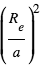 du rayonnement
du rayonnement 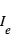 de l’étoile, et en réémet une fraction
de l’étoile, et en réémet une fraction 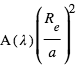 où
où 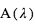 est appelé l’albédo géométrique. Ceci correspond donc à une profondeur de l'éclipse secondaire égale à :
est appelé l’albédo géométrique. Ceci correspond donc à une profondeur de l'éclipse secondaire égale à : 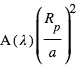 .
.
Comme 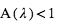 (et peut être <<1) et que
(et peut être <<1) et que 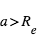 (et normalement
(et normalement 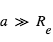 ), ceci implique le résultat intuitif que l'éclipse secondaire est (beaucoup) moins profonde que le transit primaire. Pour un albédo caractéristique de 10%, la profondeur de l'éclipse secondaire dans la composante stellaire réfléchie est de
), ceci implique le résultat intuitif que l'éclipse secondaire est (beaucoup) moins profonde que le transit primaire. Pour un albédo caractéristique de 10%, la profondeur de l'éclipse secondaire dans la composante stellaire réfléchie est de 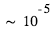 pour un Jupiter chaud à 0.05 UA (contre 0,01 pour le transit). Pour une Terre à 1 UA de même albédo, elle vaudrait
pour un Jupiter chaud à 0.05 UA (contre 0,01 pour le transit). Pour une Terre à 1 UA de même albédo, elle vaudrait 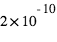 ! Si elles sont complètement hors de portée dans ce dernier cas, les mesures d’albédo sont possibles pour des Jupiters chauds (voir plus loin les résultats de Kepler) mais requièrent une haute précision photométrique et l’accumulation de nombreuses mesures.
! Si elles sont complètement hors de portée dans ce dernier cas, les mesures d’albédo sont possibles pour des Jupiters chauds (voir plus loin les résultats de Kepler) mais requièrent une haute précision photométrique et l’accumulation de nombreuses mesures.
Le contraste devient progressivement moins défavorable dans la composante thermique. Dans ce cas, le rapport 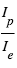 s’écrit comme le rapport des fonctions de Planck aux températures caractéristiques de la planète
s’écrit comme le rapport des fonctions de Planck aux températures caractéristiques de la planète 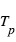 et de l’étoile
et de l’étoile 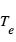 . Dans la limite des grandes longueurs d’onde, il tend vers le rapport
. Dans la limite des grandes longueurs d’onde, il tend vers le rapport 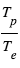 . Pour un Jupiter chaud (
. Pour un Jupiter chaud (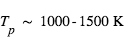 ) autour d’une étoile de type solaire, ce terme n’est plus pénalisant que d’un facteur
) autour d’une étoile de type solaire, ce terme n’est plus pénalisant que d’un facteur 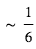 à
à 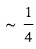 ). Ceci explique l’allure des courbes d'éclipse les plus favorables (cf. Fig. 3). Dans ce cas, il devient envisageable d’effectuer la spectroscopie de l’émission thermique.
). Ceci explique l’allure des courbes d'éclipse les plus favorables (cf. Fig. 3). Dans ce cas, il devient envisageable d’effectuer la spectroscopie de l’émission thermique.
Emission thermique de la planète
Comment résoudre l'équation de transfert radiatif
GCM
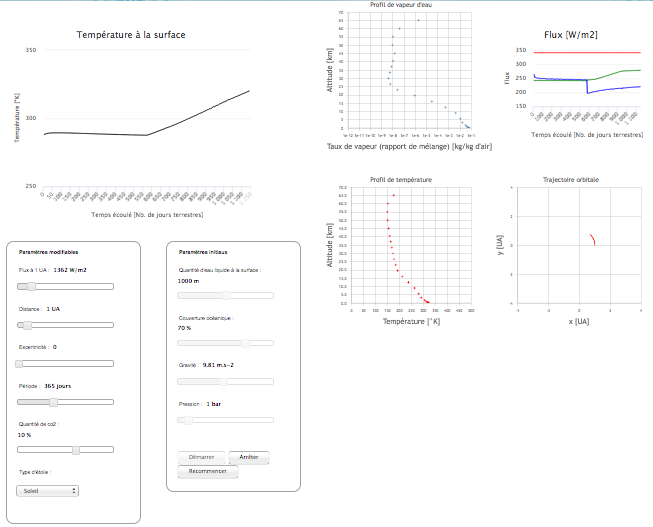
Résultat d'un GCM
Crédit :
M. Turbet, F. Forget
Une méthode dite d’inversion permet en principe de remonter aux deux paramètres, mais il est généralement impossible d’obtenir une solution unique ou même précise, compte tenu de la connaissance préalable très pauvre que l’on a des objets (contrairement aux atmosphères du Système Solaire), et le plus souvent de la qualité très modeste des spectres exoplanétaires (faibles résolution spectrale et signal-sur-bruit). Des contraintes supplémentaires peuvent être injectées pour aider à l’interprétation des spectres. Ainsi, on peut chercher des solutions physiquement cohérentes entre les profils de composition et de température, compte tenu des équilibres chimiques et de condensation entre les différents gaz et les nuages. Une autre complication est qu’on s’attend à ce que les profils atmosphériques présentent des variations horizontales considérables sur la planète (variations jour/nuit notamment), qui ne peuvent évidemment pas être appréhendées à partir d’un spectre planétaire unique.
Une approche alternative moderne est de construire des modèles atmosphériques auto-cohérents à 3 dimensions à l’aide d’outils de type MCG (modèles de circulation générale, GCM en anglais), puis de les tester en regard des observations. Il est aussi fructueux de combiner la mesure de l’émission thermique avec celle du spectre en transmission au moment du transit (cette dernière étant très sensible à la composition atmosphérique mais beaucoup moins aux détails du profil de température), tout en étant conscient que les deux mesures ne sondent pas les mêmes régions de la planète ; à nouveau le passage par un MCG peut s’avérer très utile.
Malgré tout, le plus souvent, au-delà de la présence avérée de certains gaz – H2O essentiellement – les interprétations du spectre d’un objet donné peuvent être diverses, avec des divergences sur les abondances gazeuses (parfois par des ordres de grandeurs), et sur la forme des profils de température – notamment la présence ou non de couches d’inversion (stratosphères).
Courbes de phase
La mesure de la courbe de phase est également une mesure de l’émission thermique d’une exoplanète, mais le focus est alors sur la variation photométrique de cette émission avec la position de la planète sur son orbite. Celle-ci renseigne sur les variations de la température « moyenne » (stricto sensu, la température au niveau d’émission dans l’atmosphère) le long de l’orbite. En général, comme indiqué plus haut, on a ainsi accès aux variations diurnes de température. Dans le cas d’une orbite de forte excentricité, les températures dépendent surtout de la distance à l’étoile, i.e. l’écart au périastre. Dans les deux cas, cela de permet de mesurer la constante de temps radiative de l’atmosphère, i.e. le temps caractéristique de réponse aux variations d’insolation.
Difficulté de la spectroscopie des exoplanètes
A de très rares exceptions près, la spectroscopie atmosphérique requiert une stabilité et une sensibilité qui ne peuvent être atteinte que par des moyens spatiaux. Dans l’infrarouge proche, les meilleurs spectres d’exoplanète en transit et en éclipse secondaire ont été obtenus par le télescope spatial Hubble (instruments NICMOS, STIS et surtout WFC3, couvrant 0.9 – 1.7 microns). A plus grande longueur d’onde, ces spectres ont été complétés par le spectromètre IRS (couvrant 5-14 microns) du télescope spatial Spitzer, alors que les courbes de phases proviennent le plus souvent du photomètre IRAC dans 4 bandes de longueur d’onde (3.6, 4.5, 5.8, 8.0 micron, cf Fig. 3). Dans un futur proche, les observations avec le télescope spatial JWST s'annoncent très prometteuses.
Les missions Corot et Kepler et leurs résultats
Deux missions de photométrie de haute précision
Nous terminerons par une description de deux missions spatiales dédiées (au moins partiellement) à la recherche et l’étude des transits exoplanétaires, et de leurs principaux résultats.
Corot
Corot

le satellite Corot
Crédit :
CNES
Courbe de lumière de Corot-7 b
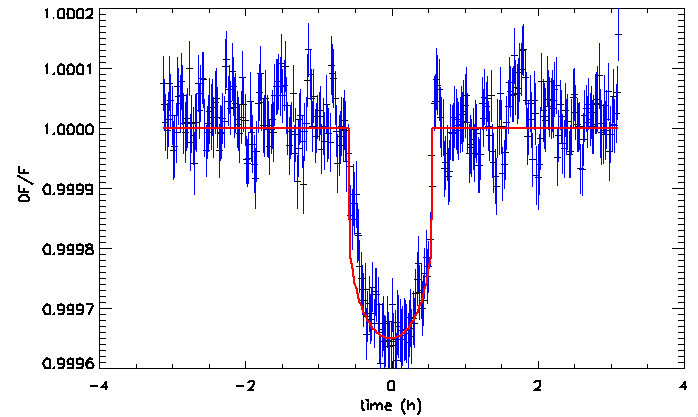
Crédit :
ESA
CoRoT (COnvection ROtation et Transits planétaires), un programme mené par le CNES en collaboration avec l’ESA, a fonctionné de janvier 2007 à décembre 2012. Ce télescope de 27 cm en orbite géocentrique polaire était équipé de 4 détecteurs CCD couvrant un champ d’environ 3.5°. CoRoT a suivi des milliers d’étoiles de magnitude 11 à 16 avec une sensibilité photométrique d’environ 0.01 %. CoRot a permis la découverte de 31 exoplanètes. Parmi celles-ci, on peut relever les cas particulièrement intéressants suivants :
CoRot 7-b, dont le rayon (1.7 rayons terrestres) et la masse (5-8 masses terrestres, mesurée ultérieurement par vitesse radiale) impliquent une densité proche ou légèrement supérieure à celle de la Terre, ce qui en fit la première exoplanète tellurique découverte. Sa période orbitale est incroyablement courte (20.5 heures) et la distance à l’étoile n’est que de 6 rayons stellaires. D’après les modèles, la température côté jour pourrait dépasser 2000°C et la surface pourrait donc se présenter comme un océan de lave.
- CoRot 1-b, première exoplanète dont l'éclipse secondaire a été observée dans la composante stellaire réfléchie
- Corot 2-b, dont le très grand rayon (1.7 rayon de Jupiter) est mal compris, et la classent parmi les planètes « enflées »
Kepler
Kepler
Nombre d'exoplanètes
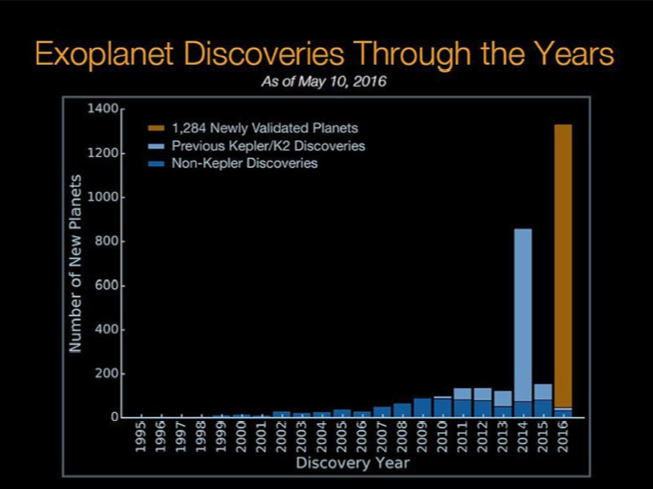
Figure 8 : Nombre d’exo-planètes découvertes par année (jusqu’au 10 mai 2016). En bleu clair et ocre, la contribution de Kepler à ces découvertes.
Crédit :
à traduire
Exoplanètes candidates de Kepler
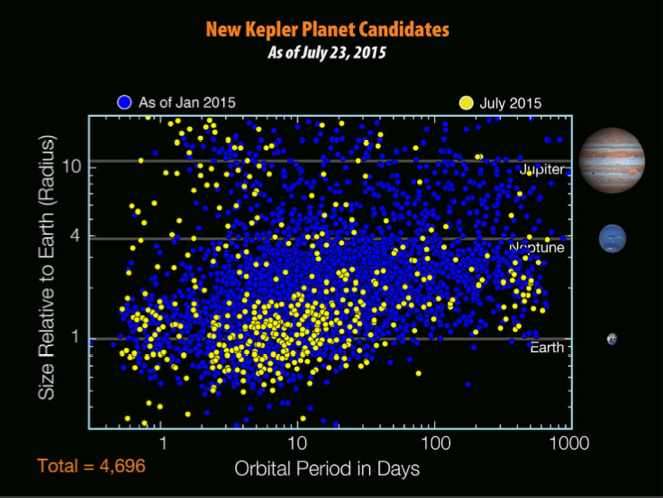
Figure 9a : Candidats planétaires Kepler (en date du 23/07/2015) dans un diagramme période / rayon.
Crédit :
à traduire
Taille des exoplanètes
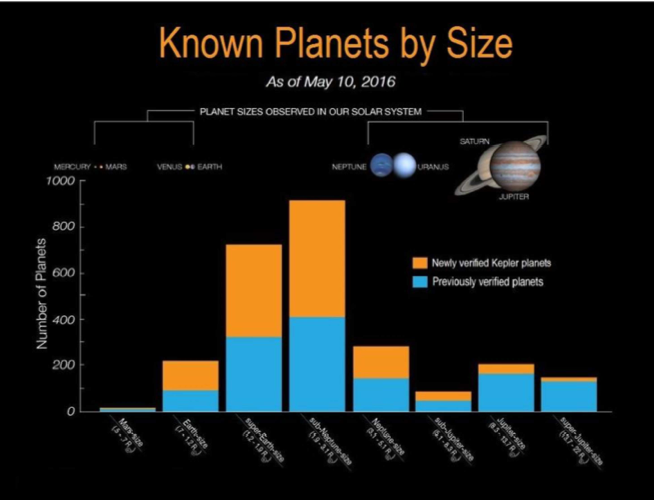
Figure 9b : Distribution des exo-planètes confirmées en fonction de leur rayon
Crédit :
à traduire
Exoplanètes dans la "zone habitable"
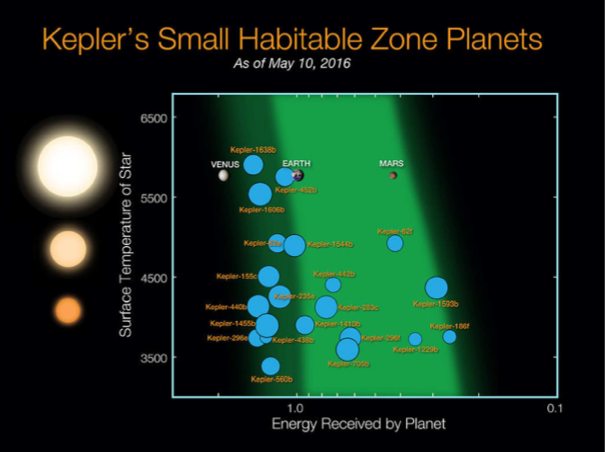
Figure 10 : Les 21 planètes de rayon inférieur à 2 rayons terrestres et se trouvant dans la zone habitable. Elles sont placées dans un diagramme montrant l’énergie qu’elles reçoivent de leur étoile (normalisée à celle reçue par la Terre du Soleil) en fonction de la température de l’étoile. Les zones vertes indiquent l’extension probable de la zone habitable selon une estimation prudente (vert clair) et optimiste (vert foncé).
Kepler, une mission du programme « Discovery » de la NASA, a été lancée en mars 2009 et a fonctionné nominalement jusqu’en mai 2013. Malgré des avaries techniques, elle a pu poursuivre son programme exoplanètes après cette date, sous le nom de mission K2. Avec un télescope de 1.4 m en orbite héliocentrique, sa précision photométrique est de 3x10-5, ce qui permet d’atteindre les planètes sub-telluriques, même si de nombreux transits sont nécessaires pour garantir des détections sans ambiguïté. Avec un champ de 115 degrés carrés, Kepler surveille en permanence 150,000 étoiles, pour la plupart de magnitude 14-16, avec une mesure photométrique toutes les 30 minutes. Un traitement automatisé détecte les «candidats », appelés aussi les Kepler Objects of Interest (KOI), i.e. les signaux pouvant indiquer le transit d’une exoplanète, mais qui doivent ensuite être inspectés/validés pour éliminer les faux positifs.
Les résultats de Kepler sont annoncés sous forme de parution régulière de liste de candidats et de planètes confirmées. Le nombre de planètes Kepler confirmées a dépassé le millier en janvier 2015, et a atteint 2325 en mai 2016 (Fig. 8). La majorité est dans la gamme des « super-Terre » (1 à 2 rayons terrestres) et « mini-Neptune » (2 à 3 rayons terrestres) (Fig. 9a, 9b). A ce jour, le nombre total d’exoplanètes confirmées découvertes par la méthode des transits est de l’ordre de 2700 (correspondant à environ 2000 systèmes planétaires), sur un total de 4000 environ. La méthode des transits est devenue, et de loin, la plus prolifique.
Outre la richesse et les études statistiques que permettent ces découvertes, on peut, comme pour CoRoT, relever quelques cas de planètes ou systèmes Kepler remarquables :
- Les planètes dans la zone habitable. Kepler 22-b, une planète de ~2 rayons terrestres, située à 0.85 AU de son étoile-hôte (de type solaire), est la première exoplanète découverte (décembre 2011) dans la zone habitable, c’est-à-dire la zone où l’eau peut être présente sous forme liquide. Des indices suggèrent une composition interne différente (plus riche en volatils) que celle de la Terre, et sa surface pourrait être couverte d’océans. Depuis, Kepler a découvert 21 planètes de rayon inférieur à 2 rayons terrestre et dans la zone habitable (Fig. 10).
- Les planètes circumbinaires, i.e. qui orbitent autour du barycentre d’un système d’étoile double. Le cas le plus célèbre est celui de Kepler 16-b (« Tatooine »). Suivant les époques, elle transite devant l’une ou l’autre des étoiles, ou les deux.
- Les systèmes contenant de nombreuses planètes : par exemple, Kepler-90 abrite sept planètes, toutes transitantes, avec des rayons de 0.12 à 1 rayon de Jupiter, et des périodes de 7 à 332 jours. Dans certains cas, ces planètes sont en résonance de période: par exemple, les 4 planètes de Kepler-223 sont en résonance 3 :4 :6 :8.
- Les planètes non transitantes découvertes par la méthode des TTV (transit time variations)
- Les planètes les plus « extrêmes ». On trouve ainsi dans le bestiaire Kepler :
- l’exoplanète la plus petite : Kepler 37-b, à peine plus grande que la Lune (0.30 rayon terrestre)
- l’exoplanète la plus chaude et la deuxième plus proche de son étoile : Kepler-70b, qui orbite en 5.8 heures et à 0.0060 UA l’étoile sous-naine B Kepler-70, a une température estimée à 7100 K. Elle est donc plus chaude que la surface du Soleil ! A noter que le système possède une seconde planète, Kepler-70c, qui orbite à 0.0076 UA. Il s’agit du couple d’exoplanètes les plus proches : au plus près, les objets sont à 240000 km l’un de l’autre (60 % de la distance Terre-Lune)
- l’exoplanète de plus fort albédo. Alors que la plupart des albédos exoplanétaires mesurés sont typiquement de 0.1 ou moins en raison de l’absorption par des espèces atmosphériques comme Na, K, TiO, VO, Kepler 10-b, une autre planète « océan de lave » a un albédo d’environ 0.5.
Se tester
Auteur: F. Roques
Se tester
Auteur: J.M. Griessmayer
 HD 189733
HD 189733
Temps :
En 2005, il n'y avait que 160 exoplanètes découvertes, la plupart par la méthode des vitesses radiales. La planète HD 189733 a été découverte par François Bouchy et son équipe au cours d'une campagne de recherche associant le spectrographe à fibres ELODIE et une caméra CDD.
Question 1)
La courbe de lumière de HD 189733
montre plusieurs phénomènes. Expliquer à quels phénomènes physiques chaque phase correspond et quels paramètres de la planète ils permettent d'estimer.
A quoi correspond le flux = 1?
Projet
Projet : Découverte de WASP-80
Ce projet a pour but de mettre en application tout votre nouveau savoir théorique pour l'appliquer à un cas pratique. Nous allons prendre des données réelles de transit, chercher si une planète s'y cache, et le cas échéant, déduire les paramètres de la planète associée, tels que son rayon et sa période. Vous comparerez alors vos résultats à ceux qui ont vraiment étaient publiés par l'équipe de recherche qui a traité ces données il y a quelques années.
Nous allons analyser des données provenant de SuperWASP qui est composé de 8 télescopes de 11cm chacun, ce qui permet de couvrir presque 500 degrés carrés sur le ciel (i.e. la surface d'environ 2500 pleines lunes à chaque prise). Il y a en fait un SuperWASP au Nord (La Palma) et un au Sud (Afrique du Sud) pour pouvoir couvrir tout le ciel (plus de détails ici ).
Voici les données historiques qui ont mené à la première détection de la planète autour de l'étoile WASP-80 en 2013. Dans ce fichier, vous trouverez les mesures photométriques de l'étoile WASP-80 (située dans la constellation de l'Aigle) à différentes dates. Les 3 colonnes indiquent respectivement la date du point photométrique (en BJD pour Barycentric Julian Date, qui donne le jour julien correspondant à l'observation), la magnitude de l'étoile mesurée à cette date, et l'erreur associée sur la magnitude.
WAST-80 : Les données
 Exercice
Exercice
Nous allons utiliser python pour ce mini-projet. Vous pouvez aussi utiliser votre langage de prédilection si Python ressemble à des hiéroglyphes pour vous.
Question 1)
Commencez par charger le fichier wasp80data.txt qui contient les observations de WASP-80 et faites un graphe représentant la magnitude en fonction du temps, avec les barres d'erreurs associées à chaque point.
En python, cela donne :
import numpy as np
import matplotlib.pyplot as plt
bjd, mag, err = np.loadtxt("wasp80data.txt", delimiter=' ', skiprows=1, unpack=True)
plt.errorbar(bjd,mag,err)
Question 2)
On pourrait travailler avec les magnitudes, mais il est plus commun de travailler directement en flux. En effet, un transit produit une baisse du flux total qui provient de l'étoile alors que ça provoque une augmentation de la magnitude et donc on ne verrait pas une baisse mais une croissance de la magnitude lors d'un transit en magnitude. Vous pourrez essayer plus loin de suivre la même procédure en travaillant sur les magnitudes (pour constater que l'on arrive aux mêmes résultats) mais pour le moment on travaillera en flux.
Reproduire le même graphique que précédemment en unité de flux
La conversion d'un Flux F à une magnitude m est telle que 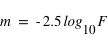
Que voyons-nous ? Est-ce ce à quoi l'on s'attend ? Voyons-nous un transit ? Pas vraiment ! Ça ne ressemble pas exactement aux courbes théoriques que l'on a vues dans le cours avec une belle chute de flux quand la planète passe devant son étoile. Pour cela il va falloir travailler un peu les données.
Un œil averti se rendra compte que ces données on été pré-traitées. On voit que la magnitude oscille autour de zéro, la composante de magnitude due à l'étoile a donc été retirée. On voit aussi que les données semblent suivre une ligne horizontale, sans qu'il y ait de variations linéaires ou polynomiales. En réalité, quand on obtient les données brutes, c'est beaucoup moins propre que cela, et il faut retirer les effets qui ne sont pas dûs au transit mais plutôt à l'observation en tant que telle. Il peut y avoir des déviations du signal dues à l'instrumentation (par exemple à cause de variations thermiques), ou même des variations de l’atmosphère au cours de l'observation. Il y a différentes méthodes pour réajuster les données afin de corriger ces variations qui ne sont pas dues au transit. De manière générale et simplifiée, cela revient à trouver une fonction polynomiale qui suit au mieux les variations à long terme et de retirer cette fonction du signal. On appelle cela le detrending. Les données que l'on traite ici ont déjà subi ce detrending et peuvent être maintenant exploitées pour chercher un transit potentiel et trouver les paramètres de la planète le cas échéant.
WASP-80 : Les transits
 La recherche des transits
La recherche des transits
Que faut-il faire pour essayer de voir un transit dans ces données ?
Ici, on a la magnitude (ou le flux) du système en fonction du temps. Pour pouvoir voir un transit, et c'est là toute la puissance de cette méthode de détection, il va falloir sommer les différents transits potentiels qu'il y a dans ces données. Pour cela, il faut trouver la bonne période sur laquelle sommer les données, et peut-être qu'alors avec une somme de plusieurs transits, on verra effectivement une courbe de lumière typique avec une baisse de flux quand la planète passe devant son étoile.
Question 1)
On peut essayer par exemple de sommer les signaux sur une période de 2 jours. En python cela donne :
from PyAstronomy.pyasl import foldAt
best_period=2#jours
phases = foldAt(bjd, best_period)
sortIndi = np.argsort(phases)
phases = phases[sortIndi]*best_period
mag = mag[sortIndi]
plt.plot(phases, mag)
Question 2)
On ne voit toujours rien. Idéalement, il faudrait pouvoir faire cela pour un très grand nombre de périodes et visualiser le résultat jusqu'à l'obtention potentielle d'une baisse de flux à un endroit de la courbe (i.e. voir le transit). C'est la méthode que l'on va utiliser, mais bien sûr, il est impossible de visualiser des millions de courbes à l'oeil et il faut trouver un bon indicateur que l'ordinateur puisse tester lui-même pour nous dire quand il y a effectivement une baisse de flux visible et donc un transit.
La méthode la plus couramment utilisée dans le domaine de la recherche est la méthode BLS (pour Box Least Square, développée par Kovacs et al. 2002). L'idée est de dire qu'un transit peut être en première approximation modélisé par une fonction porte (fonction rectangulaire). Un transit est en effet bien plus proche d'une fonction porte que d'un sinus ou cosinus car les variations lors de l'entrée ou de la sortie du transit qui peuvent être non rectangulaires ne représentent qu'une petite partie du signal et le reste du transit est plutôt plat. La décomposition en série de Fourier ne fournirait pas une fréquence donnée dominante mais plutôt un ensemble de fréquences alors que la fonction porte ne requiert qu'un terme pour bien modéliser le signal, d'où l'avantage.
On crée alors un modèle simple de fonction porte avec trois paramètres : sa profondeur, sa longueur (durée du transit) et sa phase (la date où le transit a lieu). On fait ensuite tourner le modèle sur un très grand nombre de périodes. Pour chaque période testée, l'algorithme BLS essaye de trouver les meilleurs paramètres (profondeur, longueur, phase) du modèle pour expliquer les observations. L'algorithme compare le meilleur modèle aux données et estime alors la vraisemblance (en log) du modèle en question (par exemple par une méthode des moindres carrés) et crée un périodogramme qui donne la vraisemblance du modèle en fonction de la période. On peut alors voir si certaines périodes paraissent plus vraisemblables que d'autres. Les pics dans le périodogramme indiquent la présence de planètes en transit ou du bruit non pris en compte dans le pré-traitement (detrending). Il faut faire attention aux faux-positifs avec cette méthode et les repérer est un champ actif de recherche dans lequel nous ne rentrerons pas en détails.
Trouvez la période du transit et sa profondeur dans les données de WASP-80.
Il faut utiliser la méthode BLS décrite précédemment. Soit vous la codez vous-même, soit vous utilisez une fonction pré-existente qui intègre déjà cet algorithme BLS. Il y a de telles fonctions en python ou fortran par exemple.
Question 3)
Vérifiez ces valeurs en sommant les données initiales sur la période trouvée et en affichant le flux en fonction de la phase (vous pouvez utiliser le code de la question 1 ci-dessus pour sommer les différents transits sur une période donnée). Vous produirez aussi une deuxième courbe où vous moyennerez le signal dans des bins temporels d'environ 15 minutes pour avoir une courbe de transit plus lisse.
En faisant ce travail , on trouve le diagramme de la figure ci-jointe. :
Flux stellaire
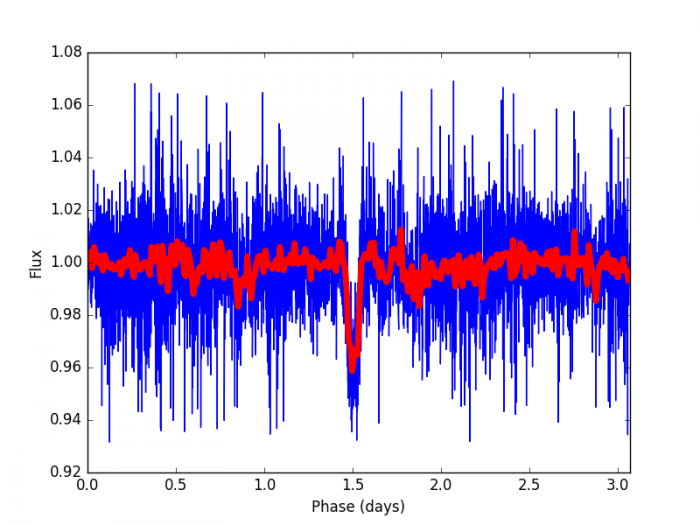
Crédit :
Q. Kral
Maintenant, on reconnaît une courbe de transit typique. On peut même zoomer sur la phase de transit pour obtenir la figure ci-jointe.
Transit
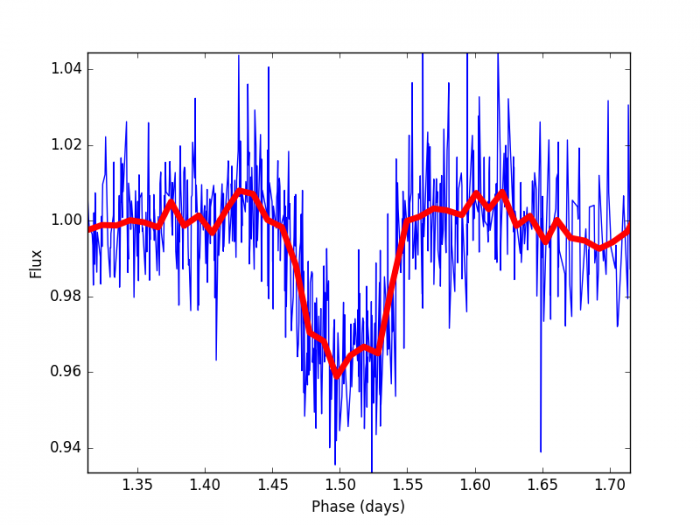
Crédit :
Q. Kral
On voit alors que la durée du transit totale est inférieure à 0.1 jours, i.e. <2.4h. Pour obtenir la courbe rouge rebinnée en python, on peut écrire un code ad hoc ou procéder ainsi :
from scipy.stats import binned_statistic
bin_means = binned_statistic(phases, mag, bins=300)
bin_means2 = binned_statistic(phases, phases, bins=300)
plt.plot(bin_means2[0], bin_means[0],color='red',linewidth=5)
WASP-80 : La planète
 WASP-80 : Les paramètres de la planète
WASP-80 : Les paramètres de la planète
Déduisez maintenant le rayon de la planète et son demi-grand axe.
Question 1)
Il faudra d'abord trouver le rayon de l'étoile WASP-80 afin de pouvoir déterminer le rayon de la planète.
Nous allons estimer le rayon de l'étoile à partir de sa température et de sa distance. La température est estimée à partir de ses magnitudes dans la couleur bleue (B) et visible (V) grâce au graphe ci-joint.

Les données de l'étoile, sa distance et ses magnitudes B et V sont données dans le tableau venant de l'article de Triaud et al. ( ci-joint). Ces données sont aussi accessibles dans la base de données Simbad

Notez que Simbad donne la parallaxe de l'étoile en milliarcseconde d'arc. La distance exprimée en parsec est l'inverse de la parallaxe exprimée en seconde d'arc.
La magnitude absolue du Soleil est de 4.83 et sa température est de 5800K.
Dans ces calculs, on utilise différentes magnitudes dont les définitions sont données ici. La magnitude visuelle est notée 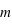 ou
ou 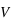 .
.
Question 2)
Le calcul du rayon de l'étoile que l'on vient de mener n'est qu'un calcul approximatif etTriaud et al. (2013) sont capable d'estimer ce rayon plus précisément à partir de leur jeu de données, ils trouvent 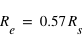 , que l'on utilisera par la suite pour comparer à leurs résultats.
, que l'on utilisera par la suite pour comparer à leurs résultats.
Maintenant on peut déduire le rayon de la planète. En supposant que l'orbite est circulaire, on peut aussi déduire facilement son rayon orbitale à partir de la 3ème loi de Kepler
On utilise Tpla= 3.0674846 jours et la masse de l'étoile est dans Triaud et al. (2013), soit 0.57Ms.
Question 3)
On peut maintenant comparer aux valeurs trouvées dans le papier originel de Triaud et al. (2013) (tableau ci-joint).
On voit que nos valeurs pour 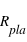 , la période et le demi-grand axe sont très proches des valeurs originelles.
, la période et le demi-grand axe sont très proches des valeurs originelles.
Paramètres du système WASP-80

article Triaud et al. 2013
On peut aussi comparer les valeurs trouvées avec celles de l'encyclopédie exoplanet.eu.
Comme vu dans le cours, on peut faire une première vérification pour tester pour un faux positif, en comparant la durée du transit théorique avec sa durée réelle que l'on a obtenue à la question 3 de la page précédente.
WASP-80 : Pour aller plus loin
Pour aller plus loin vous pouvez aussi essayer d'obtenir plus d'informations à partir des données, par exemple en utilisant, au lieu de la fonction porte, un vrai modèle de transit à la Mandel & Agol (2002) pour pouvoir déduire le paramètre d'impact et une possible excentricité en prenant en compte les effets d'assombrissement centre au bord (il y a une fonction python qui implémente ce modèle ).
Ce dossier(une fois décompressé, le fichier readme.txt décrit les différents fichiers) donne un ensemble de données qui permettent de faire d'autres analyses de cette planète:
Le dossier donne aussi des données Spitzer (infrarouge) du même système qui ont été utilisées dans Triaud et al. (2015). Dans ces données, on peut voir l'éclipse secondaire (en plus du transit) car le contraste dans l'infrarouge est plus favorable. Attention, il va falloir faire du detrending pour bien corriger les données brutes. Vous pouvez alors déduire la température de brillance de la planète. On s’attend à ce que la température d’équilibre et de brillance soient du même ordre, mais pas exactement les mêmes. On s'attend à ce que le côté jour de la planète soit légèrement plus chaud et le côté nuit légèrement en dessous de la température d’équilibre.
Pour avoir un jeu de données complet, on fournit aussi les observations en vélocimétrie radiale avec Coralie et HARPS pour ce même système afin de pouvoir aussi déterminer la masse de la planète et ainsi connaître sa densité (et donc pouvoir inférer sa composition).
Vous pouvez faire une courbe de la vitesse radiale en fonction de la phase (comme pour la courbe de transit) et voir ce qu'il se passe, en particulier pendant le transit. On peut, en effet, voir l'effet de Rossiter-McLaughlin dans les données HARPS, ce qui permet de contraindre le sens de rotation de l'orbite de la planète et l’orientation de l’orbite planétaire, à savoir l’angle entre le plan orbital et l’axe de rotation de l’étoile.
Au boulot !
-------------FIN DU CHAPITRE -------------
-------------FIN DU CHAPITRE -------------
-------------FIN DU CHAPITRE -------------
ACCES AU PLAN DES CHAPITRES
Réponses aux exercices
pages_ind-transits/taille.html
Exercice
'Transit de planètes du système solaire'
pages_ind-transits/candidates.html
Exercice
'Détectabilité des planètes par transit'
pages_ind-transits/setester.html
Exercice
'HD 189733'
- Question 1
Solution :
- Phase 0 : la planète passe devant l'étoile
- Phase 0.5 : la planète passe derrière l'étoile
- Entre la phase 0.2 et la phase 0.4, l'augmentation de surface de la planète orientée vers l'observateur
- Phase 0.2 : Nouvelle Planète (comme on parle de Nouvelle Lune)
- Phase 0.4 : Pleine Planète (comme on parle de la Pleine Lune).
Le flux = 1 correspond au flux de l'étoile.
- Question 2
Aide :
Commencez par 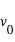 , puis
, puis 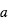 .
.
Solution :
La période est 2.219 jours, la demi-amplitude est de 205 m/s, la vitesse du système est de -2.361 km/s.
pages_ind-transits/wasp89-donnees.html
Exercice
pages_ind-transits/wasp80-recherche.html
Exercice
'La recherche des transits'
- Question 1
- Question 2
Aide :
Il faut utiliser la méthode BLS décrite précédemment. Soit vous la codez vous-même, soit vous utilisez une fonction pré-existente qui intègre déjà cet algorithme BLS. Il y a de telles fonctions en python ou fortran par exemple.
Solution :
Pour gagner du temps nous utiliserons la fonction python bls.eebls qui permet de faire tourner l'algorithme BLS en une ligne de code (il faut suivre l'installation du module ici ). On peut aussi essayer de réinventer la roue et de le développer soi-même pour comprendre tous les tenants et aboutissants de cette fonction.
Faisons appel à la fonction BLS python pour trouver notre transit.
On appellera la fonction bls.eebls où l'on doit fournir les arguments qui suivent en entrée:
bls.eebls(bjd, flux, u, v, nf, fmin, df, nb, qmi, qma)
bjd est la date. Flux est le flux ou la magnitude. Puis les autres arguments sont fixés comme ceci :
- u=np.empty(bjd.shape)
- v=np.empty(bjd.shape)
- nf=1000#nombre de bins de fréquences à tester
- fmin=1./(100.)#fréquence minimum à tester (100 jours)
- df=0.0005#taille des bins de fréquences
- nb=1000#nombre de bins à utiliser pour la courbe de lumière sommée
- qmi=0.001#durée de transit minimum à tester
- qma=0.2#durée de transit maximum à tester
On appelle ensuite la fonction avec u et v qui sont vides et servent à des calculs intermédiaires et on stocke le résultat dans la variable results :
results = bls.eebls(bjd, mag, u, v, nf, fmin, df, nb, qmi, qma)
On stocke les résultats dans différentes variables décrites ci-dessous
power, best_period, best_power, depth, q, in1, in2 = results
power est le spectre de puissance de dimension nf aux fréquences f = fmin + arange(nf) * df,
best_period est la meilleure période de transit trouvée par l'algorithme (dans la même unité que le temps mis en entrée),
best_power est la puissance (du spectre de puissance) pour cette meilleure période trouvée,
depth est la profondeur du transit pour la meilleure période,
q est la durée du transit par rapport à la période,
in1 est l'index du bin où le transit commence,
in2 est l'index du bin où le transit se termine.
Puis on crée le périodogramme résultant comme ceci :
plt.plot(np.arange(fmin, fmin+nf*df, df), power)
Cela retourne le périodogramme de la figure ci-jointe.

On constate donc qu'il y a une fréquence orbitale privilégiée à environ 0.33 orbite par jour, i.e. 1/0.326=3.067 jours par orbite. L'algorithme retourne une période (best_period) de 3.0674846 jours et une profondeur de transit (depth) de 0.0313459 pour cette meilleure période.
- Question 3
pages_ind-transits/wasp80-planete.html
Exercice
'WASP-80 : Les paramètres de la planète'
- Question 1
Aide :
Nous allons estimer le rayon de l'étoile à partir de sa température et de sa distance. La température est estimée à partir de ses magnitudes dans la couleur bleue (B) et visible (V) grâce au graphe ci-joint.

Aide :
Les données de l'étoile, sa distance et ses magnitudes B et V sont données dans le tableau venant de l'article de Triaud et al. ( ci-joint). Ces données sont aussi accessibles dans la base de données Simbad

Aide :
Notez que Simbad donne la parallaxe de l'étoile en milliarcseconde d'arc. La distance exprimée en parsec est l'inverse de la parallaxe exprimée en seconde d'arc.
Aide :
On utilise le fait que la luminosité d'une étoile est 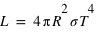 , que
, que 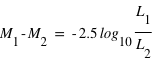 , où
, où 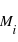 est la magnitude absolue de l'étoile
est la magnitude absolue de l'étoile 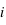 (i.e. la magnitude qu'aurait cette étoile si elle était à 10pc) et enfin que la magnitude absolue
(i.e. la magnitude qu'aurait cette étoile si elle était à 10pc) et enfin que la magnitude absolue 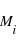 et la magnitude visuelle,
et la magnitude visuelle, 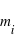 sont liées à la distance
sont liées à la distance 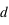 par
par 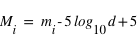
Aide :
La magnitude absolue du Soleil est de 4.83 et sa température est de 5800K.
Aide :
Dans ces calculs, on utilise différentes magnitudes dont les définitions sont données ici. La magnitude visuelle est notée 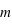 ou
ou 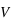 .
.
Solution :
La différence de magnitude en bande B et en bande V égale à B-V=0.93. On trouve une température d'environ 4000K. On a affaire à une étoile de type K, plus petite que notre soleil (de type G2).
La distance est 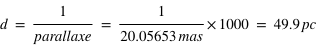 .
.
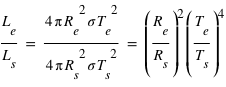 et donc
et donc 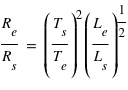 où l'index
où l'index 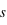 est pour le Soleil et
est pour le Soleil et 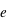 pour l'étoile WASP-80. D'après la définition de la magnitude, on a aussi que
pour l'étoile WASP-80. D'après la définition de la magnitude, on a aussi que 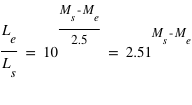 , où
, où 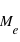 est la magnitude absolue de l'étoile. Pour transformer la magnitude mesurée
est la magnitude absolue de l'étoile. Pour transformer la magnitude mesurée 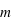 (qui dépend de la distance de l'étoile) en magnitude absolue, on utilise
(qui dépend de la distance de l'étoile) en magnitude absolue, on utilise 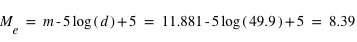 , soit
, soit 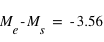 et donc on obtient
et donc on obtient 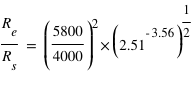 , soit
, soit 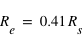 .
.
- Question 2
Aide :
On utilise Tpla= 3.0674846 jours et la masse de l'étoile est dans Triaud et al. (2013), soit 0.57Ms.
Solution :
Comme on connait la profondeur du transit de 0.0313459 et en utilisant la relation du cours sur taille de la planète, la profondeur = 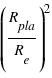 , on déduit que
, on déduit que 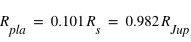 .
.
Le demi-grand axe 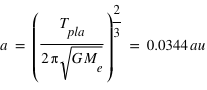 .
.
On aurait aussi pu deriver la masse en utilisant les relations entre masse et rayon ou entre masse et luminosité.
- Question 3
Solution :
Comme on a vu dans le cours, la durée du transit est égale à : 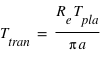 en supposant un paramètre d'impact nul. On obtient donc une durée de 0.075 jours ou 1.8 heures, ce qui est proche de ce que l'on voit sur le transit zoomé de la page précédente.
en supposant un paramètre d'impact nul. On obtient donc une durée de 0.075 jours ou 1.8 heures, ce qui est proche de ce que l'on voit sur le transit zoomé de la page précédente.






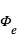 et celui de la planète
et celui de la planète 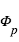 . Pendant l'éclipse secondaire, le flux mesuré est restreint à
. Pendant l'éclipse secondaire, le flux mesuré est restreint à 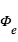 .
.
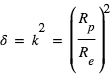 , où
, où 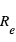 et
et 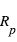 sont respectivement le rayon de l'étoile et de la planète. Le flux de lumière de l'étoile est réduit d'une fraction
sont respectivement le rayon de l'étoile et de la planète. Le flux de lumière de l'étoile est réduit d'une fraction 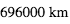 et Jupiter a un rayon de
et Jupiter a un rayon de 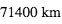 . La Terre a un rayon de
. La Terre a un rayon de 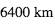 .
.
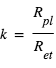 , mais également du rapport de l’intensité lumineuse spécifique (i.e. pour une surface donnée) émise par les deux objets. Comme on le verra plus loin, il dépend de de la longueur d’onde, et selon celle-ci, des températures de la planète et de l’étoile, ou de l’albédo de la planète.
, mais également du rapport de l’intensité lumineuse spécifique (i.e. pour une surface donnée) émise par les deux objets. Comme on le verra plus loin, il dépend de de la longueur d’onde, et selon celle-ci, des températures de la planète et de l’étoile, ou de l’albédo de la planète.






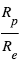 de 1.0%. L'éclipse secondaire (phase 0.5) indique que le côté jour de la planète émet 0.3% du rayonnement stellaire à cette longueur d’onde, impliquant une température d’environ 1210 K. La figure du bas (zoom vertical de celle du haut) montre la courbe de phase. Après modélisation, celle-ci indique que la température du côté nuit est d’environ 970 K, « seulement » 240 K plus froid que sur le côté jour, ce qui implique une forte redistribution de la chaleur par la dynamique atmosphérique. D’après Knutson et al. 2007.
de 1.0%. L'éclipse secondaire (phase 0.5) indique que le côté jour de la planète émet 0.3% du rayonnement stellaire à cette longueur d’onde, impliquant une température d’environ 1210 K. La figure du bas (zoom vertical de celle du haut) montre la courbe de phase. Après modélisation, celle-ci indique que la température du côté nuit est d’environ 970 K, « seulement » 240 K plus froid que sur le côté jour, ce qui implique une forte redistribution de la chaleur par la dynamique atmosphérique. D’après Knutson et al. 2007.

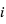 l’inclinaison entre la normale au plan orbital et la ligne de visée, il faut que l’on ait la relation :
l’inclinaison entre la normale au plan orbital et la ligne de visée, il faut que l’on ait la relation : 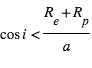 , où
, où 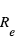 et
et 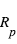 sont les rayons de l'étoile et de la planète,
sont les rayons de l'étoile et de la planète, 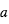 est la distance projetée entre l’étoile et planète au moment où celle-ci est au plus proche de l’observateur. Compte tenu que la planète est toujours beaucoup plus petite que l’étoile, et en se limitant pour simplifier au cas d’une orbite circulaire de demi-grand axe a, on peut montrer que la probabilité de transit et celle d'éclipse secondaire sont toutes deux égales à
est la distance projetée entre l’étoile et planète au moment où celle-ci est au plus proche de l’observateur. Compte tenu que la planète est toujours beaucoup plus petite que l’étoile, et en se limitant pour simplifier au cas d’une orbite circulaire de demi-grand axe a, on peut montrer que la probabilité de transit et celle d'éclipse secondaire sont toutes deux égales à 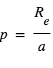 . Ceci prouve le résultat intuitif que la probabilité de transit est plus grande pour les planètes les plus proches de leur étoile.
. Ceci prouve le résultat intuitif que la probabilité de transit est plus grande pour les planètes les plus proches de leur étoile.
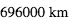 . L'orbite de la Terre a un rayon de
. L'orbite de la Terre a un rayon de 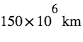 soit 1 U.A. (Unité Astronomique). L'orbite de Jupiter est à 5.2 U.A.
soit 1 U.A. (Unité Astronomique). L'orbite de Jupiter est à 5.2 U.A.
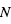
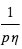 . Par exemple, les « Jupiters chauds » ont une distance type à leur étoile de 0.05 UA, et concernent environ 1 % des étoiles. Ceci donne p
. Par exemple, les « Jupiters chauds » ont une distance type à leur étoile de 0.05 UA, et concernent environ 1 % des étoiles. Ceci donne p 
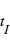 à
à 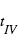 les 4 « temps de contact », c’est-à-dire les instants auxquels les disques de la planète et de l’étoile sont tangents. L’instant moyen de l’entrée (du disque planétaire devant le disque stellaire) est
les 4 « temps de contact », c’est-à-dire les instants auxquels les disques de la planète et de l’étoile sont tangents. L’instant moyen de l’entrée (du disque planétaire devant le disque stellaire) est 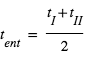 ; de même l’instant moyen de la sortie (du disque planétaire) est
; de même l’instant moyen de la sortie (du disque planétaire) est 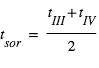 . L’intervalle de temps séparant ces deux instants, noté T, est par définition la « durée du transit », alors que
. L’intervalle de temps séparant ces deux instants, noté T, est par définition la « durée du transit », alors que 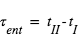 et
et 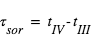 sont respectivement la durée de l’entrée et de la sortie. On note également b le « paramètre d’impact », i.e. la distance minimale – exprimée en fraction de rayon stellaire – entre la position apparente de la planète et le centre de l’étoile.
sont respectivement la durée de l’entrée et de la sortie. On note également b le « paramètre d’impact », i.e. la distance minimale – exprimée en fraction de rayon stellaire – entre la position apparente de la planète et le centre de l’étoile.
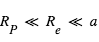 , et
, et 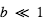 (transit non-rasant), on peut montrer que la durée du transit est égale à :
(transit non-rasant), on peut montrer que la durée du transit est égale à :
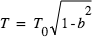 où
où 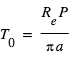 , P étant la période orbitale.
, P étant la période orbitale.
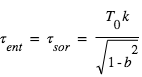 , où
, où 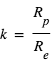 En combinant l’expression de
En combinant l’expression de 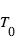 ci-dessus avec la 3eme loi de Kepler, et en se ramenant au cas du système solaire, on obtient
ci-dessus avec la 3eme loi de Kepler, et en se ramenant au cas du système solaire, on obtient 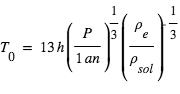 expression dans laquelle la seconde parenthèse représente le rapport de la densité de l’étoile à celle du Soleil. Ainsi, vu depuis une autre étoile, le transit de la Terre devant le Soleil ne dure que 13 h une fois tous les ans, et celui de Jupiter ne dure que 30 h une fois tous les douze ans, ce qui illustre à nouveau la rareté du phénomène. Bien évidemment, la mesure de la période requiert l’observation d’au moins deux transits.
expression dans laquelle la seconde parenthèse représente le rapport de la densité de l’étoile à celle du Soleil. Ainsi, vu depuis une autre étoile, le transit de la Terre devant le Soleil ne dure que 13 h une fois tous les ans, et celui de Jupiter ne dure que 30 h une fois tous les douze ans, ce qui illustre à nouveau la rareté du phénomène. Bien évidemment, la mesure de la période requiert l’observation d’au moins deux transits.

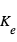 sur l’étoile est relié à la masse planétaire par :
sur l’étoile est relié à la masse planétaire par :
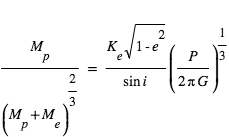 où
où 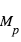 et
et 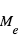 sont la masse planétaire et stellaire, e l’excentricité, P la période, et G la constante universelle de gravitation. L’avantage ici est qu’on peut écrire
sont la masse planétaire et stellaire, e l’excentricité, P la période, et G la constante universelle de gravitation. L’avantage ici est qu’on peut écrire 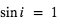 .
.

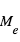 n’est pas connue. Il faut donc combiner les mesures de transit et de vitesse radiale avec des informations indépendantes sur l’étoile, typiquement obtenues via les modèles d’évolution stellaire, qui donnent des relations entre âge, luminosité, rayon, masse et composition.
n’est pas connue. Il faut donc combiner les mesures de transit et de vitesse radiale avec des informations indépendantes sur l’étoile, typiquement obtenues via les modèles d’évolution stellaire, qui donnent des relations entre âge, luminosité, rayon, masse et composition.
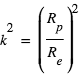 , la durée du transit T et la durée de l’ingress/egress contraignent le rapport
, la durée du transit T et la durée de l’ingress/egress contraignent le rapport 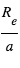 et le paramètre d’impact b, ce qui permet de « calibrer » le rayon planétaire en absolu. Si les propriétés stellaires sont suffisamment bien connues, on peut donc obtenir des valeurs absolues du rayon et de la masse planétaire, donc de sa densité, ce qui a évidemment une importance énorme pour contraindre la nature (gazeuse, glacée, rocheuse) et la structure interne de la planète.
et le paramètre d’impact b, ce qui permet de « calibrer » le rayon planétaire en absolu. Si les propriétés stellaires sont suffisamment bien connues, on peut donc obtenir des valeurs absolues du rayon et de la masse planétaire, donc de sa densité, ce qui a évidemment une importance énorme pour contraindre la nature (gazeuse, glacée, rocheuse) et la structure interne de la planète.
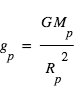 indépendamment des propriétés de l’étoile :
indépendamment des propriétés de l’étoile :
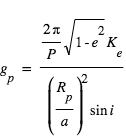 La connaissance de
La connaissance de 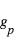 est nécessaire pour l’élaboration de modèles d’atmosphères.
est nécessaire pour l’élaboration de modèles d’atmosphères.

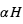 , où H est la hauteur d’échelle de l’atmosphère et
, où H est la hauteur d’échelle de l’atmosphère et 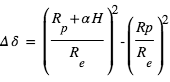
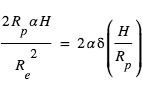
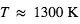 ,
, 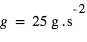 , masse moléculaire = 2 amu (
, masse moléculaire = 2 amu (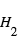 ),
), 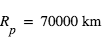 ), on obtient
), on obtient 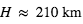 , ce qui fait
, ce qui fait 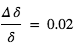 en adoptant
en adoptant 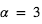 . Pour une "Terre" (
. Pour une "Terre" (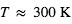 ,
, 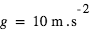 , masse moléculaire = 28 amu (
, masse moléculaire = 28 amu (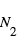 ),
), 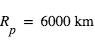 ), on trouve
), on trouve 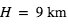 et
et 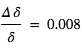 , en prenant toujours
, en prenant toujours 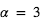 .
.
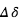 est donc inférieur à
est donc inférieur à 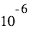 , ce qui illustre l’extrême difficulté de ce type de mesures.
, ce qui illustre l’extrême difficulté de ce type de mesures.
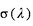 la section efficace d’absorption à la longueur d’onde
la section efficace d’absorption à la longueur d’onde 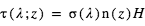 , où
, où 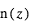 est la concentration de l’espèce absorbante à l’altitude z. Comme le transit sonde les couches au limbe, l’opacité le long de la ligne de visée est multipliée par le facteur géométrique d’augmentation du parcours
est la concentration de l’espèce absorbante à l’altitude z. Comme le transit sonde les couches au limbe, l’opacité le long de la ligne de visée est multipliée par le facteur géométrique d’augmentation du parcours 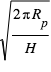 , et vaut donc :
, et vaut donc : 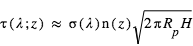 On peut montrer que le rayon planétaire effectif à la longueur d’onde
On peut montrer que le rayon planétaire effectif à la longueur d’onde 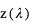 pour laquelle l’opacité en visée horizontale vaut environ 0.56 :
pour laquelle l’opacité en visée horizontale vaut environ 0.56 : 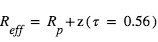 Comme
Comme 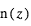 est relié à la concentration
est relié à la concentration 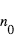 à la surface, selon
à la surface, selon 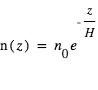 , on peut en déduire
, on peut en déduire
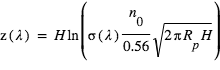 ce qui confirme que l’augmentation du rayon effectif est essentiellement proportionnelle à H (le terme dans le ln variant lentement avec H).
ce qui confirme que l’augmentation du rayon effectif est essentiellement proportionnelle à H (le terme dans le ln variant lentement avec H).
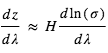 Si l’on connaît le mécanisme physique responsable de l’absorption (par exemple, la diffusion Rayleigh où
Si l’on connaît le mécanisme physique responsable de l’absorption (par exemple, la diffusion Rayleigh où 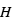 , donc une estimation de sa composition principale si la température peut être estimée indépendamment.
, donc une estimation de sa composition principale si la température peut être estimée indépendamment.
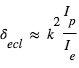 où
où 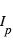 et
et 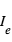 sont les intensités (par élément de surface) émises par la planète et l’étoile et
sont les intensités (par élément de surface) émises par la planète et l’étoile et 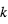 est le rapport des rayons
est le rapport des rayons 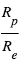 .
.
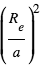 du rayonnement
du rayonnement 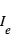 de l’étoile, et en réémet une fraction
de l’étoile, et en réémet une fraction 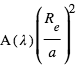 où
où 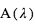 est appelé l’albédo géométrique. Ceci correspond donc à une profondeur de l'éclipse secondaire égale à :
est appelé l’albédo géométrique. Ceci correspond donc à une profondeur de l'éclipse secondaire égale à : 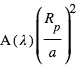 .
.
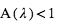 (et peut être <<1) et que
(et peut être <<1) et que 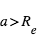 (et normalement
(et normalement 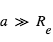 ), ceci implique le résultat intuitif que l'éclipse secondaire est (beaucoup) moins profonde que le transit primaire. Pour un albédo caractéristique de 10%, la profondeur de l'éclipse secondaire dans la composante stellaire réfléchie est de
), ceci implique le résultat intuitif que l'éclipse secondaire est (beaucoup) moins profonde que le transit primaire. Pour un albédo caractéristique de 10%, la profondeur de l'éclipse secondaire dans la composante stellaire réfléchie est de 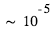 pour un Jupiter chaud à 0.05 UA (contre 0,01 pour le transit). Pour une Terre à 1 UA de même albédo, elle vaudrait
pour un Jupiter chaud à 0.05 UA (contre 0,01 pour le transit). Pour une Terre à 1 UA de même albédo, elle vaudrait 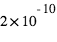 ! Si elles sont complètement hors de portée dans ce dernier cas, les mesures d’albédo sont possibles pour des Jupiters chauds (voir plus loin les
! Si elles sont complètement hors de portée dans ce dernier cas, les mesures d’albédo sont possibles pour des Jupiters chauds (voir plus loin les 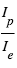 s’écrit comme le rapport des fonctions de Planck aux températures caractéristiques de la planète
s’écrit comme le rapport des fonctions de Planck aux températures caractéristiques de la planète 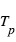 et de l’étoile
et de l’étoile 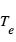 . Dans la limite des grandes longueurs d’onde, il tend vers le rapport
. Dans la limite des grandes longueurs d’onde, il tend vers le rapport 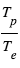 . Pour un Jupiter chaud (
. Pour un Jupiter chaud (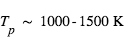 ) autour d’une étoile de type solaire, ce terme n’est plus pénalisant que d’un facteur
) autour d’une étoile de type solaire, ce terme n’est plus pénalisant que d’un facteur 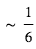 à
à 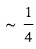 ). Ceci explique l’allure des courbes d'éclipse les plus favorables (cf. Fig. 3). Dans ce cas, il devient envisageable d’effectuer la spectroscopie de l’émission thermique.
). Ceci explique l’allure des courbes d'éclipse les plus favorables (cf. Fig. 3). Dans ce cas, il devient envisageable d’effectuer la spectroscopie de l’émission thermique.
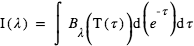 où
où 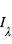 est l’intensité lumineuse sortante à la longueur d'onde
est l’intensité lumineuse sortante à la longueur d'onde 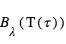 est la fonction de Planck à la température
est la fonction de Planck à la température 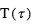 du niveau atmosphérique d’opacité
du niveau atmosphérique d’opacité 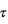 , et où l’intégrale porte sur l’ensemble de l’atmosphère. Essentiellement, l’information sur le profil de température est contenue dans la fonction de Planck, alors que le profil vertical d’opacité contraint la composition chimique.
, et où l’intégrale porte sur l’ensemble de l’atmosphère. Essentiellement, l’information sur le profil de température est contenue dans la fonction de Planck, alors que le profil vertical d’opacité contraint la composition chimique.







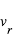 est la vitesse radiale de l'étoile
est la vitesse radiale de l'étoile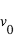 est la vitesse radiale du centre de gravité du système
est la vitesse radiale du centre de gravité du système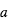 est la demi-amplitude de la sinusoïde
est la demi-amplitude de la sinusoïde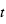 est le temps en Jours Julien
est le temps en Jours Julien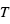 est la période de révolution de la planète autour de l'étoile
est la période de révolution de la planète autour de l'étoile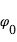 est la phase
est la phase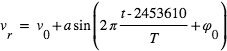
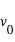 , puis
, puis 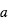 .
.
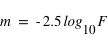


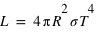 , que
, que 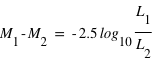 , où
, où 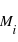 est la magnitude absolue de l'étoile
est la magnitude absolue de l'étoile 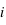 (i.e. la magnitude qu'aurait cette étoile si elle était à 10pc) et enfin que la magnitude absolue
(i.e. la magnitude qu'aurait cette étoile si elle était à 10pc) et enfin que la magnitude absolue 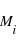 et la magnitude visuelle,
et la magnitude visuelle, 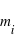 sont liées à la distance
sont liées à la distance 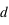 par
par 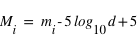
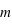 ou
ou 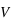 .
.
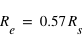 , que l'on utilisera par la suite pour comparer à leurs résultats.
, que l'on utilisera par la suite pour comparer à leurs résultats.
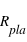 , la période et le demi-grand axe sont très proches des valeurs originelles.
, la période et le demi-grand axe sont très proches des valeurs originelles.

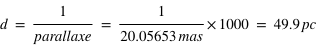 .
.
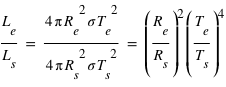 et donc
et donc 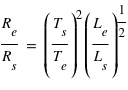 où l'index
où l'index 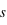 est pour le Soleil et
est pour le Soleil et 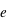 pour l'étoile WASP-80. D'après la définition de la magnitude, on a aussi que
pour l'étoile WASP-80. D'après la définition de la magnitude, on a aussi que 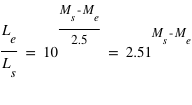 , où
, où 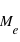 est la magnitude absolue de l'étoile. Pour transformer la magnitude mesurée
est la magnitude absolue de l'étoile. Pour transformer la magnitude mesurée 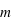 (qui dépend de la distance de l'étoile) en magnitude absolue, on utilise
(qui dépend de la distance de l'étoile) en magnitude absolue, on utilise 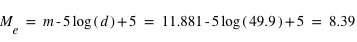 , soit
, soit 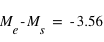 et donc on obtient
et donc on obtient 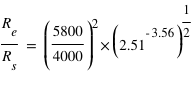 , soit
, soit 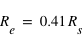 .
.
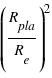 , on déduit que
, on déduit que 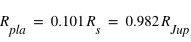 .
.
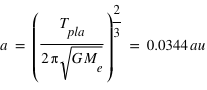 .
.
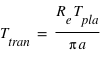 en supposant un paramètre d'impact nul. On obtient donc une durée de 0.075 jours ou 1.8 heures, ce qui est proche de ce que l'on voit sur le transit zoomé de la page précédente.
en supposant un paramètre d'impact nul. On obtient donc une durée de 0.075 jours ou 1.8 heures, ce qui est proche de ce que l'on voit sur le transit zoomé de la page précédente.