| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
La spirale de Parker |
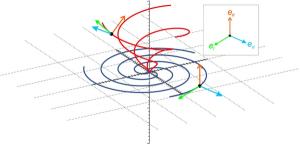
Nous avons vu précédemment que le champ magnétique solaire approche celui d'un dipole puis s'ouvre lorsque l'on s'éloigne du soleil à partir d'une distance appelé source surface, 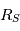 . Dans le milieu interplanétaire,
. Dans le milieu interplanétaire, 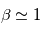 , i.e., le plasma du vent solaire impose son mouvement au champ magnétique. La forme du champ B interplanétaire est alors une combinaison entre le flot radial du plasma du vent solaire et d'un champ magnétique radial en rotation (On suppose les pieds du champ magnétique fixé à la surface du soleil).
, i.e., le plasma du vent solaire impose son mouvement au champ magnétique. La forme du champ B interplanétaire est alors une combinaison entre le flot radial du plasma du vent solaire et d'un champ magnétique radial en rotation (On suppose les pieds du champ magnétique fixé à la surface du soleil).
En supposant que le vent solaire et le champ magnéique s'étendent seulement en 2 dimension, on a : 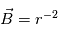 . En coordonnées sphériques, on suppose un champ magnétique à symétrie de révolution :
. En coordonnées sphériques, on suppose un champ magnétique à symétrie de révolution : 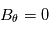 et azimuthale :
et azimuthale : 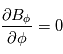 . On développe alors la condition
. On développe alors la condition 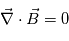 (équation de Maxwell), et on obtient :
(équation de Maxwell), et on obtient :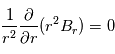 . En intégrant, on obtient entre la source surface et une distance
. En intégrant, on obtient entre la source surface et une distance 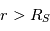 :
:
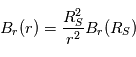 .
Si l'on suppose que la structure du milieu interplanétaire est stationnnaire,
.
Si l'on suppose que la structure du milieu interplanétaire est stationnnaire, 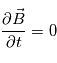 , on peut calculer
, on peut calculer 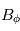 à partir de l'équation d'induction :
à partir de l'équation d'induction : 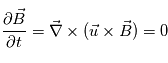 .
.
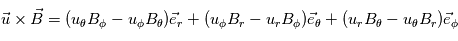
Le vent solaire et le champ magnétique s'étend en 2D, donc 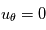 et
et 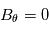
On se retrouve alors avec : 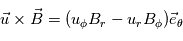
En utilisant l'expression du rotationel d'un vecteur et en ne gardant que les termes contenant la composante θ de ce vecteur, on obtient :
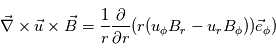
En intégrant de la surface source RS à une distance r, on obtient : 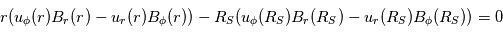 . A la surface source, B est radial, i.e.
. A la surface source, B est radial, i.e. 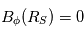 , et
, et 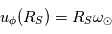 , où ω est la vitesse angulaire du Soleil.
, où ω est la vitesse angulaire du Soleil.
Finalement, 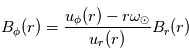 . Pour un distance r grande,
. Pour un distance r grande, 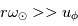 et
et 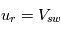 la vitesse du vent solaire, on a
la vitesse du vent solaire, on a 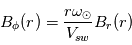 .
.
Pour déterminer la forme du champ magnétique interplanétaire, il faut calculer les lignes de forces du champ, i.e, les lignes co-linéaire au champ magnétique en tout point : On peut alors montrer que les lignes de forces ont une forme de spirale d'archimède.
Une ligne de force est une courbe qui est tangente partout au champ magnétique, i.e., 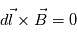
Déterminer l'équation des lignes de forces du champ magnétique interplanétaire.