La connexion Soleil - planète

La connexion Soleil-planète

Dans le cadre des relations Soleil - planète, le champ magnétique interplanétaire a un rôle déterminant.

1. C'est lui qui connecte magnetiquement le Soleil et les planètes. Lorsque des particules accélérées vont s'échapper vers l'espace interplanétaire, elle vont suivre les lignes du champ interplanétaire. Si les particules voyagent sur des lignes non-connecté à la Terre, elles ne l'impacteront pas. Cette notion est illustré sur le shéma.
2. Lorsqu'une éjection de masse coronale se propage dans l'espace interplanétaire, elle interagit directement avec son milieu environnant, ce qui a pour effet de modifier son champ magnétique par erosion, son taux d'expansion en fonction de la pression exterieur, son accélération, i.e., son temps d'arrivée sur Terre

Dans une situation ou le milieu interplanétaire suit la spirale de Parker, on peut déterminer la région à la surface solaire ou doit avoir lieu une éruption pour que les particules atteignent la Terre. Dans le plan de l'ecliptique, on définit l''angle que fait la ligne de champ avec l'axe terre soleil tel que : 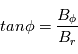. D'après l'expression du champ magnétique interplanétaire, l'angle 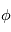dépend de la vitesse du vent solaire et de la distance au Soleil A la Terre, 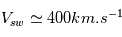, et 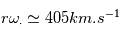, ce qui donne .

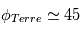En utilisant les équations des lignes de champs, on peut alors calculer la position, 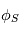du pied de la ligne à la surface source. La vitesse andulaire du Soleil est 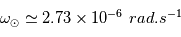. A la Terre, on a 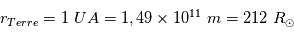avec 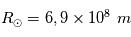, et l'angle 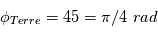. Pour une surface source 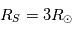, on a :

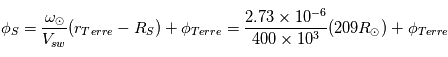
D'après le calcul ci-dessus, pour que les particules énergétiques arrivent à la Terre, l'éruption solaire devrait avoir lieu à proximité du pied de la spirale de Parker connectée à la Terre, c'est a dire à l'Ouest solaire autour de 45 degré.