Cas général

Auteur: Gary Quinsac

Dans le cas général où nous ne disposons pas de plusieurs mesures de directions non parallèles effectuées au même instant, le problème d'estimation devient dépendant du temps. Bien que des méthodes récursives basées sur l'algorithme QUEST aient été développées et utilisées, le filtrage de Kalman est le moyen le plus utilisé pour estimer l'attitude d'un satellite en présence de bruits de mesure.

Filtre de Kalman

Le filtre de Kalman a été développé en 1960 comme une nouvelle approche pour le filtrage linéaire et les problèmes de prédiction. Il permet de maintenir une estimation de l'état d'un système dynamique en dehors des périodes d'observation, à partir d'un modèle de son erreur. Puisqu'il s'agit d'un filtre récursif, la quantité d'informations à traiter reste limitée, ce qui en fait un filtre très apprécié à bord des satellites. On a pour habitude de distinguer deux phases dans ce type de filtres, la prédiction et la mise à jour :

la phase de prédiction intervient lorsqu'aucune observation n'est disponible ; le filtre se base sur le modèle dynamique embarqué pour mettre à jour les paramètres estimés, tout en mettant à jour la matrice de covariance de l'erreur d'estimation ; cette dernière augmente durant cette phase en raison de l'incertitude inhérente au modèle dynamique,
la mise à jour intervient lorsqu'une observation est disponible ; il devient alors possible de comparer la prédiction à l'observation ; les prédictions sont ainsi mises à jour, en tenant compte des incertitudes liées à l'observation et à la prédiction. Si les incertitudes liées aux observations sont plus faibles que celle du modèle alors cette phase fait décroître la covariance.

Filtre de Kalman discret

C'est la version la plus simple du filtre de Kalman, seules l'estimation de l'état précédent et les mesures actuelles sont nécessaires.

Processus à estimer

Ici, le processus stochastique à estimer est gouverné par une équation différentielle linéaire :

$\bold x_k = [A]_k \ \bold x_{k-1} + [B]_k \ \bold u_{k-1} + \bold w_{k-1}$

La mesure devant permettre l'estimation s'écrit :

$\bold z_k = [H]_k \ \bold x_k + \bold v_k$

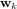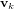$\bold w_k$ et $\bold v_k$ représentent respectivement les bruits de processus et de mesure. On les suppose indépendants, blancs et de distribution de probabilité normale. [A] est la matrice qui relie l'état précédent k-1 à l'état actuel k, [B] est la matrice qui relie l'entrée de commande $\bold u$ à l'état $\bold x$ . [H] est la matrice reliant l'état $\bold x$ à sa mesure $\bold z$ .

Phase de prédiction

Durant la phase de prédiction, l'état et l'estimation de la covariance sont projetés dans le temps de l'état k-1 à l'état k :

$\hat{\bold x}_{k|k-1} = [A]_k \ \hat{\bold x}_{k-1|k-1} + [B]_k \ \bold u_{k-1}$
$[P]_{k|k-1} = [A]_k \ [P]_{k-1|k-1} \ {[A]_k}^T + [Q]_k$

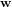[Q] est la matrice de covariance du bruit de processus $\bold w$ , $[P]_{k|k-1}$ est la matrice d'estimation a priori de la covariance de l'erreur.

Phase de mise à jour

Trois étapes se succèdent dans la phase de mise à jour. Il faut d'abord calculer le gain de Kalman [K] , puis générer une estimation de l'état a posteriori en incorporant la mesure. Enfin, on obtient la matrice de covariance de l'erreur d'estimation a posteriori $[P]_{k|k}$ .

$[K]_k = [P]_{k|k-1} {[H]_k}^T \ {[S]_k}^{-1}$
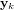$\hat{\bold x}_{k|k} = \hat{\bold x}_{k|k-1} + [K]_k \ \bold y_k$
$[P]_k = \left( [I] - [K]_k \ [H]_k \right) [P]_{k|k-1}$

[I] est la matrice identité. Deux équations supplémentaires permettent d'obtenir l'innovation, ou résiduel, $\bold y_k$ , et la covariance de l'innovation [S]_k :

$\bold y_k = \bold z_k - [H]_k \ \hat{\bold x}_{k|k-1}$
$[S]_k = [H]_k \ [P]_{k|k-1} \ {[H]_k}^T + [R]_k$

À chaque étape le processus est répété afin d'obtenir de nouvelles estimations a posteriori à partir des estimations a priori. En pratique, la matrice de covariance [R] du bruit de mesure est déterminée avant d'utiliser le filtre et peut être mise à jour par la suite. Il est plus compliqué de déterminer la matrice de covariance du bruit de processus [Q] car nous ne pouvons généralement pas directement observer le processus à estimer. Afin d'améliorer les performances du filtre, il est habituel de régler ces deux paramètres.

La plupart des systèmes physiques, et notamment ceux étudiés, sont non linéaires. Le filtre de Kalman classique n'est donc optimal que sur une faible portion des phénomènes pris en compte. Dans le cas de systèmes non-linéaires, nous utilisons donc un filtre de Kalman étendu, ou "Extended Kalman Filter".