Exercices

Ecrantage dans un plasma

Difficulté : ☆☆

On considère une charge test 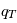q_T située en un point O placée dans un plasma dont le densité particulaire, à la distance r de O, peut s'écrire pour les ions :

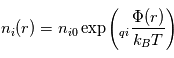
$n_i(r) = n_{i0}\exp\left(_q_i\frac{\Phi(r)}{k_BT}\right)$

et pour les électrons :

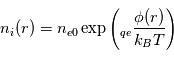
$n_i(r) = n_{e0}\exp\left(_q_e\frac{\phi(r)}{k_BT}\right)$

où 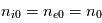$n_{i0}=n_{e0}=n_0$ (hypothèse de quasi-neutralité du plasma) est la densité particulaire moyenne, 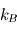k_B est la constante de Boltzmann, 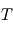est la température, 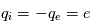q_i=-q_e=e est la chage des particules, et 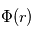$\Phi(r)$ est le potentiel qui règne à la distance 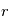de O.

Question 1)

Déterminer la densité voulumique 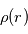$\rho(r)$

Question 2)

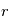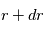En appliquant le théorème de Gauss entre deux sphères de rayons et r+dr , donner l'équation satisfaite par le champ électrostatique. En déduire une équation différentielle de deuxième ordre sur le potentiel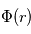 $\Phi(r)$

Aide

Question 3)

On se place dans le cas de haute températures $k_BT \gg e\Phi(r)$ . Simplifier l'équation précédente et la résoudre. La solution approche le potentiel de Coulomb de q_T quand $r\longrightarrow 0$ et reste finie à toutes les distances.

Aide Aide

Quantité macroscopique

Difficulté : ☆

On considère une fonction de distribution de vitesse Maxwellienne de la forme :

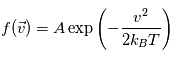
$f(\vec{v}) = A\exp\left(-\frac{v^2}{2k_BT}\right)$

avec 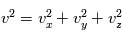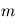v^2=v_x^2+v_y^2+v_z^2 , la masse des particules, 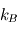k_B la constante de Boltzamnn, 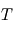la température et 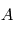une quantité réelle.

Question 1)

Déterminer 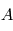telle que

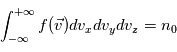
$\int_{-\infty}^{+\infty}f(\vec{v})dv_xdv_ydv_z = n_0$

où 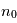n_0 est la densité des particules

Question 2)

Montrer que :

$<\frac{1}{2}mv_x^2 > = \frac{1}{2}k_B_T$

Aide

Question 3)

Montrer que :

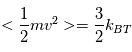
$<\frac{1}{2}mv^2> = \frac{3}{2}k_B_T$

Question 4)

Comment représenter mathématiquement une distribution de vistesse Maxwellienne avec une vitesse de dérive 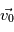$\vec{v_0}$

Question 5)

Déterminer la distribution en énergie de la fonction de distribution de vitesse précédente

Aide

Auteur: R. Modolo

Mouvement d'une particule chargée dans un champ électromagnétique

Difficulté : ☆ Temps : 15 min

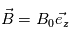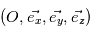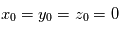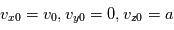On considère une particule de charge électrique q et de masse m plongée dans un champ magnétique uniforme $\vec{B}=B_0\vec{e_z}$ . On cherche à déterminer le mouvement de la particule dans ce champ magnétique. On se place dans un repère cartésien orthonormé $(O,\vec{e_x},\vec{e_y},\vec{e_z})$ . A t=0 la position de la particule est telle que x_0=y_0=z_0=0 et sa vitesse intiale est définie par $v_{x0}=v_0, v_{y0} = 0, v_{z0}=a$ .

Question 1)

Dans un premier temps on considère que le champ électrique est nul. Ecrire les équations de mouvement de la particule

Aide

Question 2)

Résoudre ces équations en utilisant les conditions initiales

Aide

Question 3)

Quelle est la trajectoire de cette particule ? La tracer.

Question 4)

On considère maintenant que la particule est toujours plangé dans le magnétique 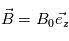$\vec{B}=B_0\vec{e_z}$ mais qu'un champ électrique est désormais présent tel que 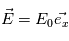$\vec{E}=E_0\vec{e_x}$ . Comment la trajectoire est-elle modifiée ?

Aide

Auteur: R. Modolo

Champ magnétique créé par une bobine torique

Difficulté : ☆ Temps : 15 min

Soit une bobine sphérique constituée d'un enroulement de N spires circulaires de rayon r parcourue par le même courant I. Ces N spires entourent réglièrement un tore de rayon R de section circulaire de rayon r<R.

Question 1)

Montrer que le champ magnétique est nul en dehors du tore et déterminer son expression à l'intérieur de celui-ci en fonction de la distance 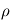$\rho$ à l'axe du tore.

Aide

Question 2)

Déterminer les valeurs extrêmes du champ magnétique pour N=500, I=0.1 mA, R=10cm et r=1cm. Quel courant devrait-on faire passer dans un fil rectiligne unique pour obtenir le même champ à la même distance ?

Aide

Auteur: Ronan Modolo

Etude d'un analyseur électrostatique à plaque parallèle

Difficulté : ☆

On considère le montage de la figure suivante. Une particule chargée de charge q (>0) entre dans le dispositif en (0,0) avec une vitesse 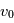v_0 , et avec un angle 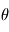$\theta$ entre le vecteur vitesse de la particule et l'axe x du montage. On cherche à caractériser le mouvement de cetteparticule chargée.

Question 1)

Dans quelle sens est dirigée le champ électrique E qui apparait entre les deux plaques parallèles? Quelle relation a-t-on entre le potentiel Va et le champ électrique E ?

Question 2)

Déterminer les conditions initiales du problème pour la position et la vitesse de la particule.

Aide

Question 3)

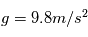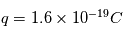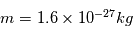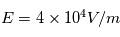
Déterminer les forces qui s'appliquent à cette particule et simplifier éventuellement le problème. On pourra prendre les valeurs numériques suivantes : g = 9.8 m/s^2 , $q = 1.6\times 10^{-19} C$ , $m=1.6\times 10^{-27} kg$ , $E=4\times 10^4 V/m$

Aide

Question 4)

Déterminer l'équation paramétrique de la trajectoire (x(t), y(t)).

Aide

Question 5)

Dans l'hypothèse où la particule n'atteint pas la plaque supérieure, déterminer le temps auquel la particule chargée atteint le sommet de sa trajectoire puis sa coordonée y.

Aide

Question 6)

Au bout de combien de teps la particule impacte-t-elle la plaque du bas ? A quelle distance de la position d'entrée ?

Aide