La troisième loi de Kepler (1618)

Auteur: Valérie Ciarletti et Lucie Maquet

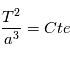
Loi des périodes : Le carré de la période de révolution T d'une planète sur son orbite est proportionnel au cube du demi-grand axe de l'ellipse. $\frac{T^2}{a^3}=Cte$

Pour un système planétaire donné, plus une planète est éloignée de son étoile, plus sa période est grande. Il est important de ne pas tirer de conclusions fausses sur les vitesses relatives de ces planètes. En effet, lorsque les orbites en question ne sont pas des cercles, la vitesse de déplacement de la planète n'est pas constante en accord avec la loi des aires.

Cette loi ayant été établie dans notre système solaire, il pouvait sembler à Kepler que la constante était universelle. Nous verrons par la suite que les lois de la mécanique permettent de calculer cette constante et que la valeur de la constante dépend de la masse de l'étoile. On montre que

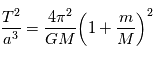
$\frac{T^2}{a^3}=\frac{4\pi^2}{GM}{\left(1+\frac{m}{M}\right)}^2$

où 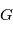est la constante de gravitation universelle et 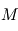la masse de l'étoile et 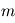celle de la planète.

Dans le cas très fréquent où la masse de l'étoile 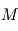est très supérieure à celle de la planète 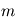, la relation devient 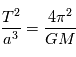$\frac{T^2}{a^3}=\frac{4\pi^2}{GM}$ et seule la masse de l'étoile intervient.

Troisième loi de Kepler

Question 1)

Utilisez la boite à outils diagrammes pour représenter pour l'ensemble des exoplanètes du catalogue leur période de révolution autour de son étoile en fonction de la valeur du demi-grand axe de leur ellipse.

Aide

Question 2)

En échelle logarithmique pour les deux axes montrez que les points sont tous sur des droites de même pente. Expliquez pourquoi, sur le diagramme obtenu, les points ne sont pas tous alignés sur la même droite.

Aide Solution