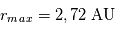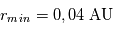Les exoplanètes, comme les planètes et autres corps de notre système solaire sont soumises à la loi de la gravitation ou attraction universelle. Cette loi a été historiquement formalisée par Isaac Newton en 1687. Elle permet de modéliser, de façon générale, l'attraction entre des corps ayant une masse et, par conséquent, le mouvement des corps célestes.
Copernic
Modèle héliocentrique de Copernic , Caelestial Orbes, 1576
Bien avant Newton, le mouvement des planètes dans le ciel a retenu l'attention de nombreux scientifiques (Aristote, Galilée, Copernic,...) qui ont proposé des modèles pour expliquer ou, au moins, modéliser leurs observations.
Les travaux de Copernic font date avec sa proposition en 1543 d'un modèle héliocentrique qui présente, entre autres, le grand avantage de simplifier les calculs par rapport au modèle géocentrique. Cependant, la cause du mouvement n'est pas identifiée et les orbites des planètes restent des cercles.
Johannes Kepler établit, à partir des observations minutieuses du mouvement de Vénus, Mars, Jupiter et Saturne faites par Tycho Brahe, le fait que les orbites des planètes de notre système solaire ne sont pas des cercles mais des ellipses dont le Soleil est un foyer. Il publie, en 1609 et 1619, des lois empiriques qui prendront le nom de Lois de Kepler. Ces lois sont particulièrement intéressantes et utiles parce qu'elles établissent des relations entre les différents paramètres des orbites. En outre, il faut noter que Kepler a certainement ouvert la voie à Newton en affirmant que "deux corps voisins et hors de la sphère d'attraction d'un troisième corps s'attireraient en raison directe de leur masse."
Newton a finalement modélisé la gravitation est ainsi permis une explication des phénomènes observés ainsi que la possibilité de prédire le mouvement des planètes en orbite autour de leur soleil. Les lois de la gravitation de Newton permettront d'ailleurs d'expliquer les résultats empiriques énoncés dans les lois de Kepler.
Notons que la mécanique classique issue des lois de Newton n'est elle-même qu'une approximation, qui ne rend plus bien compte des mouvements des corps aux vitesses très élevées ou au voisinage immédiat des masses. Ainsi c'est la relativité générale d'Einstein qui a permis d'expliquer le mouvement du périhélie de Mercure ce qui n'était pas possible à partir des lois de Newton.
Kepler

Portait de Johannes Kepler (1571-1630) réalisé en 1610 - Artiste inconnu
Brahe

Portait de Tycho Brahe (1546-1601) réalisé en 1596 - Artiste inconnu
Les trois lois de Kepler ont été établies à partir de l'observation du mouvement des planètes au sein de notre système solaire. Elles ne reposent sur aucune modélisation mécanique de l'interaction entre la planète et le soleil.
Néanmoins, ces lois seront confirmées, a posteriori, par la théorie de la gravitation universelle.
Dans cette partie, ces lois sont énoncées sans démonstration (les démonstrations seront faites plus loin) et illustrées.
Loi des orbites : Les planètes autour de leur soleil ont un mouvement périodique dans un plan. Plus précisément, ces orbites sont des ellipses dont le soleil est un foyer.
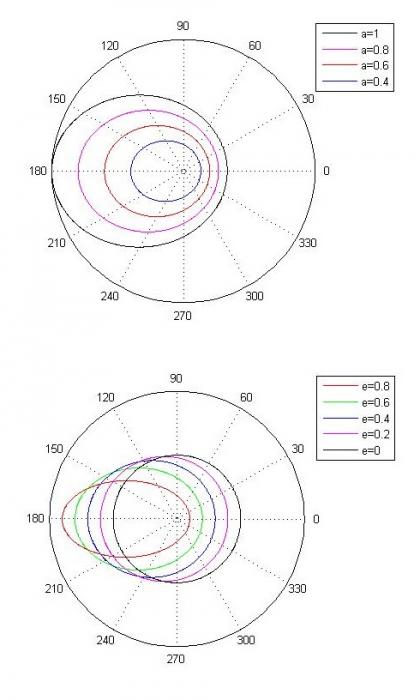
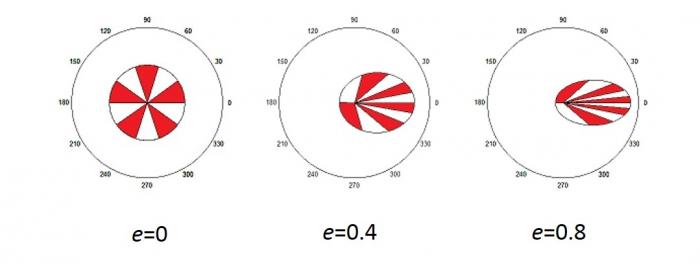
Haut : Effet de la valeur de l'excentricté e sur la forme de l'ellipse
Bas : Effet de la valeur du demi-grand axe a sur la taille de l'ellipse
 Forme des orbites
Forme des orbites
Question 1)
Exprimer la distance étoile-planète lorsque la planète est à son apoastre. Même question lorsqu'elle est située à son périastre .
On a la relation qui donne la distance en fonction de l'angle 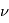 :
: 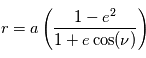
Question 2)
Calculer, en utilisant les données du catalogue des exoplanètes, la valeur munérique de ces deux distances pour l'exoplanète détectée à ce jour, ayant la valeur d'excentricité la plus élevée du catalogue.
Dans le catalogue, classer les planètes par value d'excentricité décroissante pour identifier l'exoplanète recherchée.
Question 3)
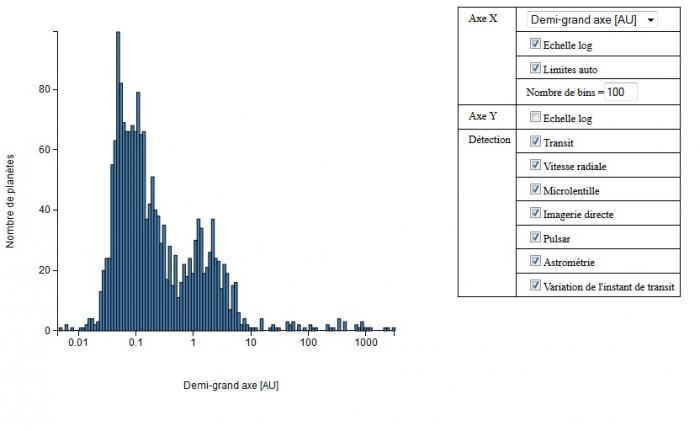
Utiliser les données du catalogue des exoplanètes et l'outil histogrammes pour étudier la variabilité des excentricités des exoplanètes.
Estimez l'excentricité moyenne des exoplanètes détectées à ce jour
Tracez l'histogramme des excentricités et pensez à diminuer le nombre de bins de l'histogramme pour obtenir simplement une valeur approchée de la moyenne des excentricités.
Auteur: Valérie Ciarletti
 Dimension des orbites
Dimension des orbites
L'objectif de cet exercice est d'étudier les tailles des ellipses des exoplanètes qui ont été détectées à ce jour en utilisant les données du catalogue et les outils qui permettent de les visualiser.
Question 1)
La taille d'une ellipse est donnée par la valeur de son demi-grand axe a. Pensez à utiliser l'échelle logarithmique.
Question 2)
Utilisez la boite à outils diagrammes pour rechercher un lien entre taille et forme des ellipses.
Loi des aires : En un temps donné, le segment qui joint le centre du soleil au centre de la planète en orbite balaie une surface (aire) égale quelle que soit la position de la planète sur l'orbite.
- Dans le cas particulier où l'orbite est un cercle (excentricté
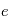 nulle), la distance planète-étoile est constante et la vitesse de déplacement de la planète sur son orbite est constante. On a un mouvement circulaire uniforme.
nulle), la distance planète-étoile est constante et la vitesse de déplacement de la planète sur son orbite est constante. On a un mouvement circulaire uniforme. - Si l'orbite est une ellipse
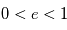 , la distance planète-étoile varie en fonction de la position de la planète sur son orbite, sa vitesse de déplacement également. Plus la planète est proche de son étoile, plus elle va vite.
, la distance planète-étoile varie en fonction de la position de la planète sur son orbite, sa vitesse de déplacement également. Plus la planète est proche de son étoile, plus elle va vite.
Illustration de la loi des aires
Pour chacun des graphes, le temps de parcours les secteurs colorés ont des aires égales
Loi des périodes : Le carré de la période de révolution T d'une planète sur son orbite est proportionnel au cube du demi-grand axe de l'ellipse.
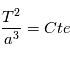
Pour un système planétaire donné, plus une planète est éloignée de son étoile, plus sa période est grande.
Il est important de ne pas tirer de conclusions fausses sur les vitesses relatives de ces planètes. En effet, lorsque les orbites en question ne sont pas des cercles, la vitesse de déplacement de la planète n'est pas constante en accord avec la loi des aires.
Cette loi ayant été établie dans notre système solaire, il pouvait sembler à Kepler que la constante était universelle. Nous verrons par la suite que les lois de la mécanique permettent de calculer cette constante et que la valeur de la constante dépend de la masse de l'étoile. On montre que
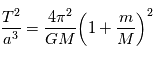
où 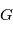 est la constante de gravitation universelle et
est la constante de gravitation universelle et 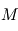 la masse de l'étoile et
la masse de l'étoile et 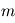 celle de la planète.
celle de la planète.
Dans le cas très fréquent où la masse de l'étoile 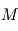 est très supérieure à celle de la planète
est très supérieure à celle de la planète 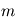 , la relation devient
, la relation devient
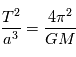 et seule la masse de l'étoile intervient.
et seule la masse de l'étoile intervient.
 Troisième loi de Kepler
Troisième loi de Kepler
Question 1)
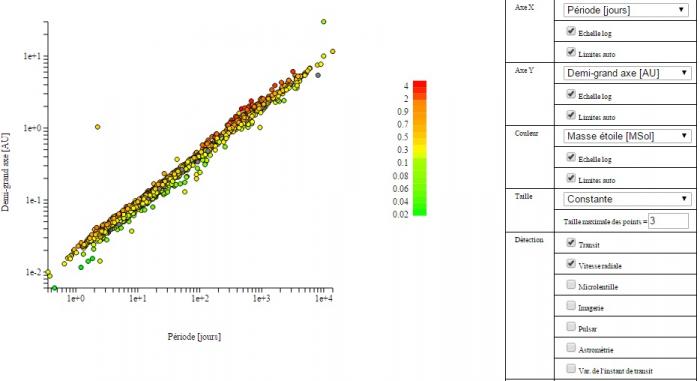
Utilisez la boite à outils diagrammes pour représenter pour l'ensemble des exoplanètes du catalogue leur période de révolution autour de son étoile en fonction de la valeur du demi-grand axe de leur ellipse.
Pensez à utiliser les échelles logarithmiques pour mettre en évidence une relation du type 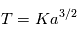
Question 2)
En échelle logarithmique pour les deux axes montrez que les points sont tous sur des droites de même pente.
Expliquez pourquoi, sur le diagramme obtenu, les points ne sont pas tous alignés sur la même droite.
Utiliser le code couleur de l'outil diagramme pour visualiser la masse de l'étoile et vérifier que ce paramètre explique largement le décalage des droites qui sont toutes parallèles.
L'attraction gravitationnelle, dans le cas d'un système planète-étoile isolé, permet de démontrer les lois de Kepler et de calculer le mouvement des deux corps. (Ces calculs sont présentés dans la partie comprendre).
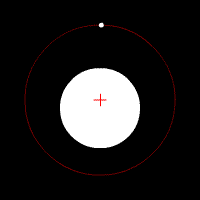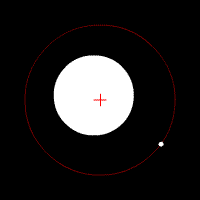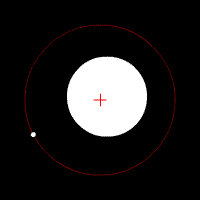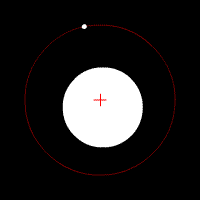
Les animations ci-dessous illustrent l'effet de cette force d'attraction en fonction du rapport des deux masses en jeu. La croix rouge imobile correspond au centre de gravité (barycentre) de l'ensemble.
mouvement de deux corps de même masse
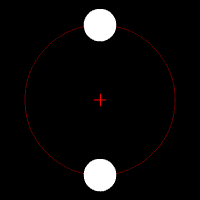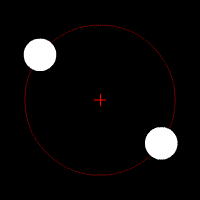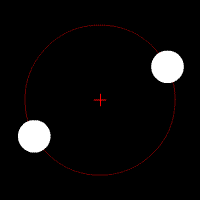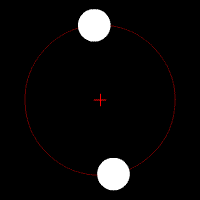
mouvement de deux corps de masse très différente
Au cours de la formation et de l'évolution d'un système planétaire, plusieurs types de migrations planétaires peuvent avoir lieu. On distingue trois types de migration de planètes. Les deux premiers types de migrations ont lieu lorsque la proto-étoile est toujours entourée d'un disque soit de gaz (migration de type I) soit de planétésimaux (migration de type II).
- La migration de type I : elle a lieu lorsqu'une proto-planète d'une masse comparable à la masse terrestre intéragit avec le disque de gaz. La migration s'exerce de l'extérieur vers l'intérieur et fait donc tomber la planète vers son étoile. Cette migration est rapide comparée à la durée de vie du disque
- La migration de type II : elle a lieu lorsque la proto-planète atteint une masse de plus de dix fois celle de la Terre. Elle creuse alors un sillon dans le disque de gaz. Le disque spiralant vers l'étoile va entrainer la proto-planète vers l'astre dans une migration lent comparée à la durée de vie du disque.
Après la dispersion du disque de gaz et de planétésimaux, les planètes peuvent toujours intéragir avec les petits corps rescapés de l'accrétion planétaire. Étant donnée la composition actuelle des planètes Uranus et Neptune (elles contiennent, toutes deux, un coeur solide : signe qu'elles ont du se former plus proche du Soleil), il y a de forts soupçons sur le fait que la migration tardive des planètes du Système solaire soit responsable de l'orbite actuelle d'Uranus et Neptune à, respectivement, 20 et 30 UA du Soleil.
Ces migrations planétaires sont notamment une explication plausible pour l'existence des " Jupiters chauds " : planètes trés massives et trés proches de leur étoile.
Pour en savoir plus sur les migrations planétaires : voir la page en suivant le lien.




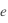 (
( 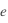 est un nombre sans dimension
est un nombre sans dimension 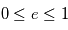 ) qui décrit le degré d'allongement de l'ellipse.
Le cercle est le cas particulier qui correspond à
) qui décrit le degré d'allongement de l'ellipse.
Le cercle est le cas particulier qui correspond à 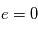 . Le cas particulier
. Le cas particulier 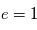 correspond à une parabole (qui ne convient pas pour une orbite fermée mais décrit la chute des corps ).
La trajectoire de la planète sur son orbite est décrite en coordonnées polaires par la relation
correspond à une parabole (qui ne convient pas pour une orbite fermée mais décrit la chute des corps ).
La trajectoire de la planète sur son orbite est décrite en coordonnées polaires par la relation 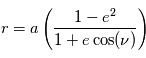 . Sous cette forme, la distance r est mesurée par rapport au centre de l'étoile (qui est sur l'un des foyers) et l'angle polaire
. Sous cette forme, la distance r est mesurée par rapport au centre de l'étoile (qui est sur l'un des foyers) et l'angle polaire 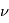 est appelé l'anomalie vraie.
est appelé l'anomalie vraie.
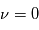 correspond à la direction du point de l'ellipse le plus proche de l'étoile. Cette position qui correspond à la distance planète-étoile minimale est appelée périastre (périhélie pour la Terre qui tourne autour du Soleil). L' apoastre (aphélie dans le cas de la Terre ) est la position qui correspond à la distance planète-étoile maximale.
correspond à la direction du point de l'ellipse le plus proche de l'étoile. Cette position qui correspond à la distance planète-étoile minimale est appelée périastre (périhélie pour la Terre qui tourne autour du Soleil). L' apoastre (aphélie dans le cas de la Terre ) est la position qui correspond à la distance planète-étoile maximale.
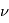 :
: 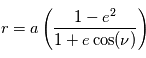
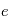 nulle), la distance planète-étoile est constante et la vitesse de déplacement de la planète sur son orbite est constante. On a un mouvement circulaire uniforme.
nulle), la distance planète-étoile est constante et la vitesse de déplacement de la planète sur son orbite est constante. On a un mouvement circulaire uniforme. 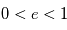 , la distance planète-étoile varie en fonction de la position de la planète sur son orbite, sa vitesse de déplacement également. Plus la planète est proche de son étoile, plus elle va vite.
, la distance planète-étoile varie en fonction de la position de la planète sur son orbite, sa vitesse de déplacement également. Plus la planète est proche de son étoile, plus elle va vite.
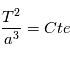
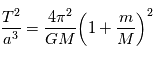
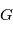 est la constante de gravitation universelle et
est la constante de gravitation universelle et 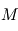 la masse de l'étoile et
la masse de l'étoile et 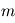 celle de la planète.
celle de la planète.
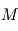 est très supérieure à celle de la planète
est très supérieure à celle de la planète 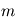 , la relation devient
, la relation devient
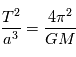 et seule la masse de l'étoile intervient.
et seule la masse de l'étoile intervient.
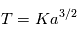


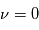 et
et 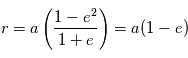 c'est la distance minimale
A l'apoastre,
c'est la distance minimale
A l'apoastre, 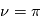 et
et 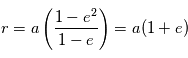 c'est la distance maximale
c'est la distance maximale