| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Datation relative |
La désintégration radioactive permet également de dater des corps même bien après la disparition des radionucléotides concernés (c'est à dire bien au delà du temps de 1/2-vie de la désintégration concernée). C’est le cas par exemple de la désintégration 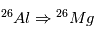 , dont le temps de ½ vie est de « seulement » 720 000ans. Notons que ni
, dont le temps de ½ vie est de « seulement » 720 000ans. Notons que ni 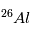 , ni
, ni 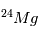 ne sont des isotopes naturels de leurs éléments, qui sont, respectivement,
ne sont des isotopes naturels de leurs éléments, qui sont, respectivement, 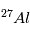 et
et 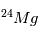 . A la différence de la désintégration d’
. A la différence de la désintégration d’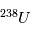 , il n’existe aujourd’hui plus de
, il n’existe aujourd’hui plus de 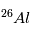 que l’on puisse mesurer. En principe, on a donc :
que l’on puisse mesurer. En principe, on a donc :
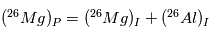
Cette équation n’est pas d’une grande aide en elle-même, mais, comme pour la datation absolue, on peut tirer parti de la non-homogénéité d’une météorite donnée. Si en effet deux endroits de cette météorite avaient initialement des teneurs totales en 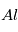 (tous isotopes confondus) différentes, mais que la proportion de
(tous isotopes confondus) différentes, mais que la proportion de 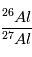 était, elle, la même, alors l’excès de
était, elle, la même, alors l’excès de 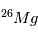 ne sera aujourd’hui pas partout le même, et cet excès sera relié à l’abondance actuelle locale de
ne sera aujourd’hui pas partout le même, et cet excès sera relié à l’abondance actuelle locale de 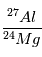 par la relation :
par la relation :
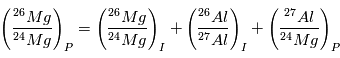
Les mesures de 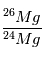 et
et 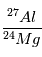 en différents endroits de la météorite
vont alors tracer une isochrone dont la pente donnera la teneur initiale en
en différents endroits de la météorite
vont alors tracer une isochrone dont la pente donnera la teneur initiale en
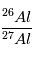 (voir Figure).
(voir Figure).
Maintenant, si on compare les teneurs initiales de 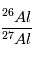 obtenus pour
différentes météorites, on peut obtenir une datation relative des temps de
formation de ces météorites. En effet, étant donné le temps de vie très court
de
obtenus pour
différentes météorites, on peut obtenir une datation relative des temps de
formation de ces météorites. En effet, étant donné le temps de vie très court
de 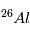 , sa teneur par rapport à
, sa teneur par rapport à 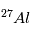 pourra être très différente suivant l’instant
où la météorite s’est formée. Si on compare les valeurs
pourra être très différente suivant l’instant
où la météorite s’est formée. Si on compare les valeurs 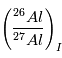 dans 2
météorites différentes, on obtient ainsi la datation relative de leur formation
par la formule:
dans 2
météorites différentes, on obtient ainsi la datation relative de leur formation
par la formule:
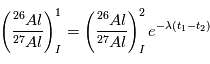
où 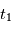 et
et 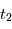 sont les instants de formation des 2 météorites, et
sont les instants de formation des 2 météorites, et 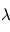 est le taux de
désintégration de la réaction
est le taux de
désintégration de la réaction 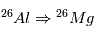
Il faut cependant ici bien faire attention à deux points très importants :
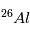 était uniformément
distribué dans la nébuleuse initiale. Les dernières recherches semblent cependant montrer que tel était bien le cas.
était uniformément
distribué dans la nébuleuse initiale. Les dernières recherches semblent cependant montrer que tel était bien le cas. 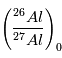 estimée correspond à ce qu’elle était au moment
de la dernière condensation de l’objet. En effet, quand le corps est dans un
état fluide (gaz, liquide), les abondances de
estimée correspond à ce qu’elle était au moment
de la dernière condensation de l’objet. En effet, quand le corps est dans un
état fluide (gaz, liquide), les abondances de 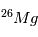 et
et 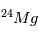 se ré-équilibrent
automatiquement à leurs proportions « naturelles » et tout excès antérieur
de
se ré-équilibrent
automatiquement à leurs proportions « naturelles » et tout excès antérieur
de 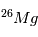 est effacé. Autrement dit, le chronomètre isotopique se « reset » lors
de tout épisode de très forte température.
est effacé. Autrement dit, le chronomètre isotopique se « reset » lors
de tout épisode de très forte température.