 |  |  |  |  |  |
| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
| | | | | |
Spectroscopie de l'éclipse secondaire |
Comme on l’a vu plus haut, l’observation de l'éclipse secondaire permet en principe de déterminer par différence la quantité de radiation que nous envoie une exoplanètes, que ce soit sous forme de lumière stellaire réfléchie ou de rayonnement thermique propre. La difficulté est ici le contraste de luminosité entre la planète et l’étoile.
La profondeur de l'éclipse secondaire s'écrit :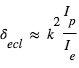
où 
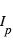et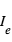 
sont les intensités (par élément de surface) émises par la planète et l’étoile et 
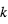est le rapport des rayons 
.
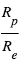Dans la composante stellaire réfléchie, juste avant l'éclipse secondaire, la planète – qui présente alors sa face entièrement éclairée – reçoit une fraction
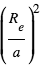du rayonnement 
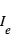de l’étoile, et en réémet une fraction 
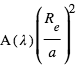où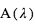 
est appelé l’albédo géométrique. Ceci correspond donc à une profondeur de l'éclipse secondaire égale à : 
.
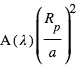Comme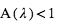 
(et peut être <<1) et que 
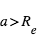(et normalement 
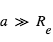), ceci implique le résultat intuitif que l'éclipse secondaire est (beaucoup) moins profonde que le transit primaire. Pour un albédo caractéristique de 10%, la profondeur de l'éclipse secondaire dans la composante stellaire réfléchie est de 
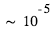pour un Jupiter chaud à 0.05 UA (contre 0,01 pour le transit). Pour une Terre à 1 UA de même albédo, elle vaudrait 
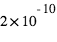! Si elles sont complètement hors de portée dans ce dernier cas, les mesures d’albédo sont possibles pour des Jupiters chauds (voir plus loin les résultats de Kepler) mais requièrent une haute précision photométrique et l’accumulation de nombreuses mesures.
Le contraste devient progressivement moins défavorable dans la composante thermique. Dans ce cas, le rapport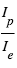 
s’écrit comme le rapport des fonctions de Planck aux températures caractéristiques de la planète 
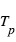et de l’étoile 
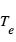. Dans la limite des grandes longueurs d’onde, il tend vers le rapport 
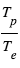. Pour un Jupiter chaud (
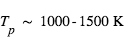) autour d’une étoile de type solaire, ce terme n’est plus pénalisant que d’un facteur 
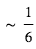à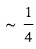 
). Ceci explique l’allure des courbes d'éclipse les plus favorables (cf. Fig. 3). Dans ce cas, il devient envisageable d’effectuer la spectroscopie de l’émission thermique.
 |  |
