Spectre en transmission de HD 209458 b
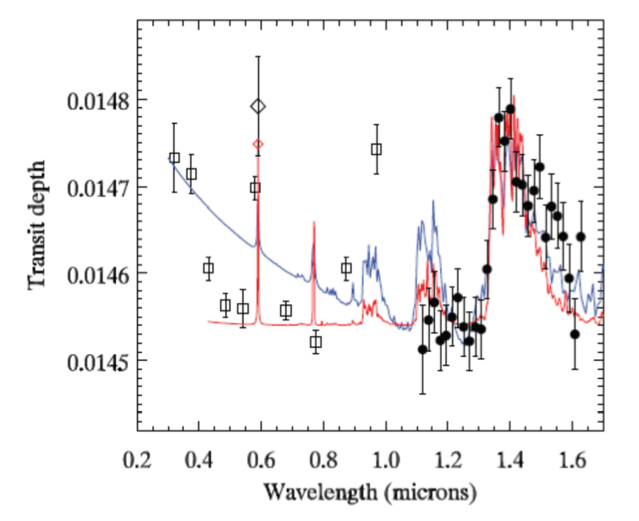
Figure 7 : Le spectre en transmission de HD 209458b, exprimé en termes de profondeur du transit. La partie visible (<1 micron) suggère l’effet de la diffusion Rayleigh et de l’absorption par le sodium à 0.58 micron. La présence de la vapeur d’eau est clairement visible à 1.4 microns (Deming et al. 2013).
Crédit :
à traduire
Comme exposé plus haut, le principe de la spectroscopie du transit est de mesurer des variations spectrales de la profondeur du transit comme diagnostic de composition atmosphérique. A une longueur d’onde où l’atmosphère absorbe, le rayon "effectif" de la planète est augmenté d’une quantité 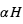 , où H est la hauteur d’échelle de l’atmosphère et α est généralement un nombre de l’ordre de quelques unités. La profondeur du transit δ est donc augmentée de :
, où H est la hauteur d’échelle de l’atmosphère et α est généralement un nombre de l’ordre de quelques unités. La profondeur du transit δ est donc augmentée de :
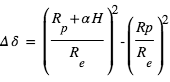 ∼
∼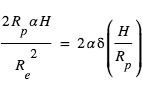
Cette relation montre fondamentalement que l’effet est d’autant plus grand que H est grande, i.e. que l’atmosphère est chaude, de faible masse moléculaire, et que la gravité est faible. Par exemple, pour un Jupiter chaud (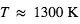 ,
, 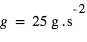 , masse moléculaire = 2 amu (
, masse moléculaire = 2 amu (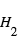 ),
), 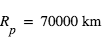 ), on obtient
), on obtient 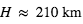 , ce qui fait
, ce qui fait 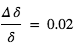 en adoptant
en adoptant 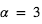 . Pour une "Terre" (
. Pour une "Terre" (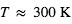 ,
, 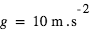 , masse moléculaire = 28 amu (
, masse moléculaire = 28 amu (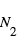 ),
), 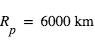 ), on trouve
), on trouve 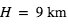 et
et 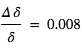 , en prenant toujours
, en prenant toujours 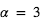 .
.
Dans les deux cas, l’ordre de grandeur est donc une augmentation relative de la profondeur du transit de l’ordre de 1% de sa valeur. Pour la planète tellurique, compte tenu que le transit géométrique est déjà inférieur à 0.01%, le signal spectral 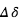 est donc inférieur à
est donc inférieur à 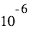 , ce qui illustre l’extrême difficulté de ce type de mesures.
, ce qui illustre l’extrême difficulté de ce type de mesures.
Echelle de hauteur
La spectroscopie du transit primaire permet d’estimer l’échelle de hauteur atmosphérique. Imaginons d’abord que le coefficient d’absorption intrinsèque de l’atmosphère varie avec la longueur d’onde λ, mais pas avec le niveau d’altitude dans l’atmosphère. Si on note 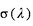 la section efficace d’absorption à la longueur d’onde λ, l’opacité en visée verticale est
la section efficace d’absorption à la longueur d’onde λ, l’opacité en visée verticale est
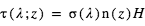 , où
, où 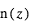 est la concentration de l’espèce absorbante à l’altitude z. Comme le transit sonde les couches au limbe, l’opacité le long de la ligne de visée est multipliée par le facteur géométrique d’augmentation du parcours
est la concentration de l’espèce absorbante à l’altitude z. Comme le transit sonde les couches au limbe, l’opacité le long de la ligne de visée est multipliée par le facteur géométrique d’augmentation du parcours 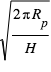 , et vaut donc :
, et vaut donc : 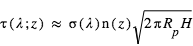 On peut montrer que le rayon planétaire effectif à la longueur d’onde λ est égal au rayon de la surface augmenté de la hauteur
On peut montrer que le rayon planétaire effectif à la longueur d’onde λ est égal au rayon de la surface augmenté de la hauteur 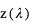 pour laquelle l’opacité en visée horizontale vaut environ 0.56 :
pour laquelle l’opacité en visée horizontale vaut environ 0.56 : 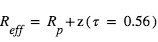 Comme
Comme 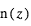 est relié à la concentration
est relié à la concentration 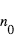 à la surface, selon
à la surface, selon 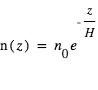 , on peut en déduire
, on peut en déduire
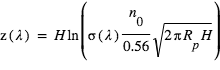 ce qui confirme que l’augmentation du rayon effectif est essentiellement proportionnelle à H (le terme dans le ln variant lentement avec H).
ce qui confirme que l’augmentation du rayon effectif est essentiellement proportionnelle à H (le terme dans le ln variant lentement avec H).
Cette expression montre que la variation du rayon effectif avec la longueur d’onde suit : 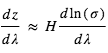 Si l’on connaît le mécanisme physique responsable de l’absorption (par exemple, la diffusion Rayleigh où σ varie comme une puissance de λ), la mesure de la variation du rayon effectif avec la longueur d’onde fournit directement la hauteur d’échelle de l’atmosphère
Si l’on connaît le mécanisme physique responsable de l’absorption (par exemple, la diffusion Rayleigh où σ varie comme une puissance de λ), la mesure de la variation du rayon effectif avec la longueur d’onde fournit directement la hauteur d’échelle de l’atmosphère 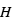 , donc une estimation de sa composition principale si la température peut être estimée indépendamment.
, donc une estimation de sa composition principale si la température peut être estimée indépendamment.
Le raisonnement précédent est valable en première approximation lorsque l’opacité atmosphérique est le fait des brumes, mais l’est moins pour une absorption par les gaz, car celle-ci dépend intrinsèquement fortement de la pression. Ce développement analytique doit donc être remplacé par des modèles numériques. Il n’en reste pas moins vrai que le spectre en transmission montre la planète « plus grosse » dans les bandes d’absorption gazeuse qu’en dehors de ces bandes, et qu’il est alors possible de contraindre la composition chimique (Fig. 7).
Les premières découvertes d’espèces chimiques dans les spectres d’exoplanètes en transmission datent des années 2002-2003 avec la détection d’espèces atomiques (Na, H, et plus tard K, C, O) dans le spectre visible. Le cas de l’hydrogène atomique est particulier car il donne lieu à des transits extrêmement profonds (15%), causés par des atmosphères d’hydrogène très étendues et en échappement rapide. Dans l’infrarouge, dû à la grande difficulté d’extraire les spectres, des controverses ont eu lieu sur la réalité et surtout la quantification des signatures spectrales en termes de paramètres atmosphériques. Il semble toutefois qu’un nombre important de ces spectres montrent les signatures spectrales de H2O, celles de CH4, CO2, et CO étant également présentes sur quelques objets. Une caractéristique très fréquente est le rôle des brumes ou nuages de haute altitude, qui contribuent à l’émission dans le spectre visible et tendent à masquer les signatures des gaz dans l’infrarouge.
Comme on l’a vu plus haut, l’observation de l'éclipse secondaire permet en principe de déterminer par différence la quantité de radiation que nous envoie une exoplanètes, que ce soit sous forme de lumière stellaire réfléchie ou de rayonnement thermique propre. La difficulté est ici le contraste de luminosité entre la planète et l’étoile.
La profondeur de l'éclipse secondaire s'écrit :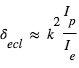 où
où 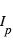 et
et 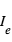 sont les intensités (par élément de surface) émises par la planète et l’étoile et
sont les intensités (par élément de surface) émises par la planète et l’étoile et 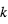 est le rapport des rayons
est le rapport des rayons 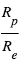 .
.
Dans la composante stellaire réfléchie, juste avant l'éclipse secondaire, la planète – qui présente alors sa face entièrement éclairée – reçoit une fraction
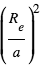 du rayonnement
du rayonnement 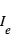 de l’étoile, et en réémet une fraction
de l’étoile, et en réémet une fraction 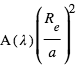 où
où 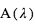 est appelé l’albédo géométrique. Ceci correspond donc à une profondeur de l'éclipse secondaire égale à :
est appelé l’albédo géométrique. Ceci correspond donc à une profondeur de l'éclipse secondaire égale à : 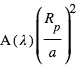 .
.
Comme 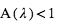 (et peut être <<1) et que
(et peut être <<1) et que 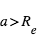 (et normalement
(et normalement 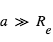 ), ceci implique le résultat intuitif que l'éclipse secondaire est (beaucoup) moins profonde que le transit primaire. Pour un albédo caractéristique de 10%, la profondeur de l'éclipse secondaire dans la composante stellaire réfléchie est de
), ceci implique le résultat intuitif que l'éclipse secondaire est (beaucoup) moins profonde que le transit primaire. Pour un albédo caractéristique de 10%, la profondeur de l'éclipse secondaire dans la composante stellaire réfléchie est de 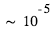 pour un Jupiter chaud à 0.05 UA (contre 0,01 pour le transit). Pour une Terre à 1 UA de même albédo, elle vaudrait
pour un Jupiter chaud à 0.05 UA (contre 0,01 pour le transit). Pour une Terre à 1 UA de même albédo, elle vaudrait 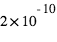 ! Si elles sont complètement hors de portée dans ce dernier cas, les mesures d’albédo sont possibles pour des Jupiters chauds (voir plus loin les résultats de Kepler) mais requièrent une haute précision photométrique et l’accumulation de nombreuses mesures.
! Si elles sont complètement hors de portée dans ce dernier cas, les mesures d’albédo sont possibles pour des Jupiters chauds (voir plus loin les résultats de Kepler) mais requièrent une haute précision photométrique et l’accumulation de nombreuses mesures.
Le contraste devient progressivement moins défavorable dans la composante thermique. Dans ce cas, le rapport 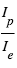 s’écrit comme le rapport des fonctions de Planck aux températures caractéristiques de la planète
s’écrit comme le rapport des fonctions de Planck aux températures caractéristiques de la planète 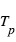 et de l’étoile
et de l’étoile 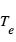 . Dans la limite des grandes longueurs d’onde, il tend vers le rapport
. Dans la limite des grandes longueurs d’onde, il tend vers le rapport 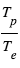 . Pour un Jupiter chaud (
. Pour un Jupiter chaud (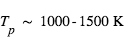 ) autour d’une étoile de type solaire, ce terme n’est plus pénalisant que d’un facteur
) autour d’une étoile de type solaire, ce terme n’est plus pénalisant que d’un facteur 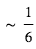 à
à 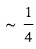 ). Ceci explique l’allure des courbes d'éclipse les plus favorables (cf. Fig. 3). Dans ce cas, il devient envisageable d’effectuer la spectroscopie de l’émission thermique.
). Ceci explique l’allure des courbes d'éclipse les plus favorables (cf. Fig. 3). Dans ce cas, il devient envisageable d’effectuer la spectroscopie de l’émission thermique.
GCM
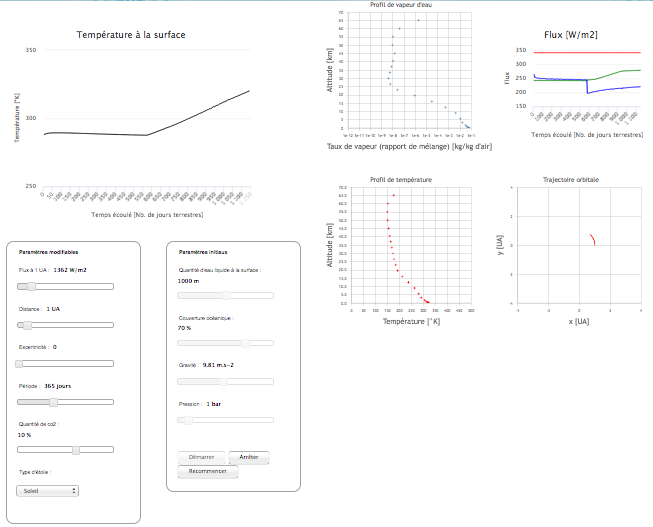
Résultat d'un GCM
Crédit :
M. Turbet, F. Forget
Une méthode dite d’inversion permet en principe de remonter aux deux paramètres, mais il est généralement impossible d’obtenir une solution unique ou même précise, compte tenu de la connaissance préalable très pauvre que l’on a des objets (contrairement aux atmosphères du Système Solaire), et le plus souvent de la qualité très modeste des spectres exoplanétaires (faibles résolution spectrale et signal-sur-bruit). Des contraintes supplémentaires peuvent être injectées pour aider à l’interprétation des spectres. Ainsi, on peut chercher des solutions physiquement cohérentes entre les profils de composition et de température, compte tenu des équilibres chimiques et de condensation entre les différents gaz et les nuages. Une autre complication est qu’on s’attend à ce que les profils atmosphériques présentent des variations horizontales considérables sur la planète (variations jour/nuit notamment), qui ne peuvent évidemment pas être appréhendées à partir d’un spectre planétaire unique.
Une approche alternative moderne est de construire des modèles atmosphériques auto-cohérents à 3 dimensions à l’aide d’outils de type MCG (modèles de circulation générale, GCM en anglais), puis de les tester en regard des observations. Il est aussi fructueux de combiner la mesure de l’émission thermique avec celle du spectre en transmission au moment du transit (cette dernière étant très sensible à la composition atmosphérique mais beaucoup moins aux détails du profil de température), tout en étant conscient que les deux mesures ne sondent pas les mêmes régions de la planète ; à nouveau le passage par un MCG peut s’avérer très utile.
Malgré tout, le plus souvent, au-delà de la présence avérée de certains gaz – H2O essentiellement – les interprétations du spectre d’un objet donné peuvent être diverses, avec des divergences sur les abondances gazeuses (parfois par des ordres de grandeurs), et sur la forme des profils de température – notamment la présence ou non de couches d’inversion (stratosphères).
La mesure de la courbe de phase est également une mesure de l’émission thermique d’une exoplanète, mais le focus est alors sur la variation photométrique de cette émission avec la position de la planète sur son orbite. Celle-ci renseigne sur les variations de la température « moyenne » (stricto sensu, la température au niveau d’émission dans l’atmosphère) le long de l’orbite. En général, comme indiqué plus haut, on a ainsi accès aux variations diurnes de température. Dans le cas d’une orbite de forte excentricité, les températures dépendent surtout de la distance à l’étoile, i.e. l’écart au périastre. Dans les deux cas, cela de permet de mesurer la constante de temps radiative de l’atmosphère, i.e. le temps caractéristique de réponse aux variations d’insolation.
Difficulté de la spectroscopie des exoplanètes
A de très rares exceptions près, la spectroscopie atmosphérique requiert une stabilité et une sensibilité qui ne peuvent être atteinte que par des moyens spatiaux. Dans l’infrarouge proche, les meilleurs spectres d’exoplanète en transit et en éclipse secondaire ont été obtenus par le télescope spatial Hubble (instruments NICMOS, STIS et surtout WFC3, couvrant 0.9 – 1.7 microns). A plus grande longueur d’onde, ces spectres ont été complétés par le spectromètre IRS (couvrant 5-14 microns) du télescope spatial Spitzer, alors que les courbes de phases proviennent le plus souvent du photomètre IRAC dans 4 bandes de longueur d’onde (3.6, 4.5, 5.8, 8.0 micron, cf Fig. 3). Dans un futur proche, les observations avec le télescope spatial JWST s'annoncent très prometteuses.

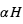 , où H est la hauteur d’échelle de l’atmosphère et α est généralement un nombre de l’ordre de quelques unités. La profondeur du transit δ est donc augmentée de :
, où H est la hauteur d’échelle de l’atmosphère et α est généralement un nombre de l’ordre de quelques unités. La profondeur du transit δ est donc augmentée de :
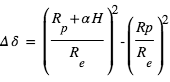 ∼
∼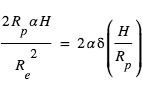
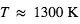 ,
, 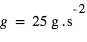 , masse moléculaire = 2 amu (
, masse moléculaire = 2 amu (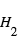 ),
), 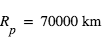 ), on obtient
), on obtient 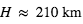 , ce qui fait
, ce qui fait 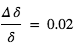 en adoptant
en adoptant 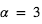 . Pour une "Terre" (
. Pour une "Terre" (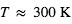 ,
, 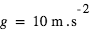 , masse moléculaire = 28 amu (
, masse moléculaire = 28 amu (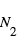 ),
), 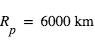 ), on trouve
), on trouve 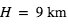 et
et 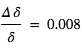 , en prenant toujours
, en prenant toujours 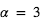 .
.
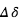 est donc inférieur à
est donc inférieur à 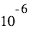 , ce qui illustre l’extrême difficulté de ce type de mesures.
, ce qui illustre l’extrême difficulté de ce type de mesures.
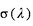 la section efficace d’absorption à la longueur d’onde λ, l’opacité en visée verticale est
la section efficace d’absorption à la longueur d’onde λ, l’opacité en visée verticale est
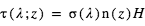 , où
, où 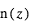 est la concentration de l’espèce absorbante à l’altitude z. Comme le transit sonde les couches au limbe, l’opacité le long de la ligne de visée est multipliée par le facteur géométrique d’augmentation du parcours
est la concentration de l’espèce absorbante à l’altitude z. Comme le transit sonde les couches au limbe, l’opacité le long de la ligne de visée est multipliée par le facteur géométrique d’augmentation du parcours 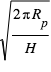 , et vaut donc :
, et vaut donc : 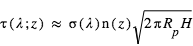 On peut montrer que le rayon planétaire effectif à la longueur d’onde λ est égal au rayon de la surface augmenté de la hauteur
On peut montrer que le rayon planétaire effectif à la longueur d’onde λ est égal au rayon de la surface augmenté de la hauteur 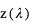 pour laquelle l’opacité en visée horizontale vaut environ 0.56 :
pour laquelle l’opacité en visée horizontale vaut environ 0.56 : 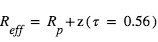 Comme
Comme 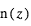 est relié à la concentration
est relié à la concentration 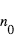 à la surface, selon
à la surface, selon 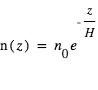 , on peut en déduire
, on peut en déduire
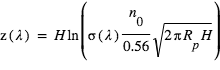 ce qui confirme que l’augmentation du rayon effectif est essentiellement proportionnelle à H (le terme dans le ln variant lentement avec H).
ce qui confirme que l’augmentation du rayon effectif est essentiellement proportionnelle à H (le terme dans le ln variant lentement avec H).
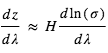 Si l’on connaît le mécanisme physique responsable de l’absorption (par exemple, la diffusion Rayleigh où σ varie comme une puissance de λ), la mesure de la variation du rayon effectif avec la longueur d’onde fournit directement la hauteur d’échelle de l’atmosphère
Si l’on connaît le mécanisme physique responsable de l’absorption (par exemple, la diffusion Rayleigh où σ varie comme une puissance de λ), la mesure de la variation du rayon effectif avec la longueur d’onde fournit directement la hauteur d’échelle de l’atmosphère 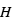 , donc une estimation de sa composition principale si la température peut être estimée indépendamment.
, donc une estimation de sa composition principale si la température peut être estimée indépendamment.
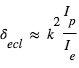 où
où 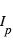 et
et 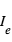 sont les intensités (par élément de surface) émises par la planète et l’étoile et
sont les intensités (par élément de surface) émises par la planète et l’étoile et 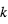 est le rapport des rayons
est le rapport des rayons 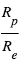 .
.
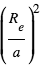 du rayonnement
du rayonnement 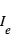 de l’étoile, et en réémet une fraction
de l’étoile, et en réémet une fraction 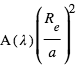 où
où 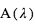 est appelé l’albédo géométrique. Ceci correspond donc à une profondeur de l'éclipse secondaire égale à :
est appelé l’albédo géométrique. Ceci correspond donc à une profondeur de l'éclipse secondaire égale à : 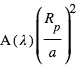 .
.
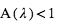 (et peut être <<1) et que
(et peut être <<1) et que 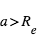 (et normalement
(et normalement 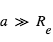 ), ceci implique le résultat intuitif que l'éclipse secondaire est (beaucoup) moins profonde que le transit primaire. Pour un albédo caractéristique de 10%, la profondeur de l'éclipse secondaire dans la composante stellaire réfléchie est de
), ceci implique le résultat intuitif que l'éclipse secondaire est (beaucoup) moins profonde que le transit primaire. Pour un albédo caractéristique de 10%, la profondeur de l'éclipse secondaire dans la composante stellaire réfléchie est de 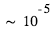 pour un Jupiter chaud à 0.05 UA (contre 0,01 pour le transit). Pour une Terre à 1 UA de même albédo, elle vaudrait
pour un Jupiter chaud à 0.05 UA (contre 0,01 pour le transit). Pour une Terre à 1 UA de même albédo, elle vaudrait 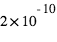 ! Si elles sont complètement hors de portée dans ce dernier cas, les mesures d’albédo sont possibles pour des Jupiters chauds (voir plus loin les
! Si elles sont complètement hors de portée dans ce dernier cas, les mesures d’albédo sont possibles pour des Jupiters chauds (voir plus loin les 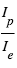 s’écrit comme le rapport des fonctions de Planck aux températures caractéristiques de la planète
s’écrit comme le rapport des fonctions de Planck aux températures caractéristiques de la planète 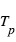 et de l’étoile
et de l’étoile 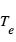 . Dans la limite des grandes longueurs d’onde, il tend vers le rapport
. Dans la limite des grandes longueurs d’onde, il tend vers le rapport 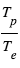 . Pour un Jupiter chaud (
. Pour un Jupiter chaud (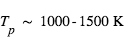 ) autour d’une étoile de type solaire, ce terme n’est plus pénalisant que d’un facteur
) autour d’une étoile de type solaire, ce terme n’est plus pénalisant que d’un facteur 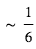 à
à 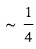 ). Ceci explique l’allure des courbes d'éclipse les plus favorables (cf. Fig. 3). Dans ce cas, il devient envisageable d’effectuer la spectroscopie de l’émission thermique.
). Ceci explique l’allure des courbes d'éclipse les plus favorables (cf. Fig. 3). Dans ce cas, il devient envisageable d’effectuer la spectroscopie de l’émission thermique.
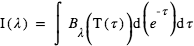 où
où 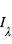 est l’intensité lumineuse sortante à la longueur d'onde
est l’intensité lumineuse sortante à la longueur d'onde 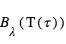 est la fonction de Planck à la température
est la fonction de Planck à la température 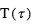 du niveau atmosphérique d’opacité
du niveau atmosphérique d’opacité 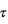 , et où l’intégrale porte sur l’ensemble de l’atmosphère. Essentiellement, l’information sur le profil de température est contenue dans la fonction de Planck, alors que le profil vertical d’opacité contraint la composition chimique.
, et où l’intégrale porte sur l’ensemble de l’atmosphère. Essentiellement, l’information sur le profil de température est contenue dans la fonction de Planck, alors que le profil vertical d’opacité contraint la composition chimique.
