Changement de connectivité

Reconnexion magnétique

Les lignes de couleurs representent les lignes de champ magnetique. De la gauche vers la droite ce schema montre le changement de connection des lignes de champ qui se cassent et se reforment en se couplant l'une a lautre.

Crédit : Obs. de Paris

Une des propriétés de la reconnexion est le changement de connectivité. Sur la figure ci-contre, premier panneau, le champ magnétique est initialement anti-parallèle. Puis sur le deuxieme panneau les lignes de champ se rapprochent l'une de l'autre. Une région de diffusion se forme à la frontière. Les lignes de champs echangent leur connectivité dans cette région de diffusion. On peut visualiser cette reconnection comme des lignes de champ qui se brisent et se recollent à l'opposé. Cette description simpliste permet de comprendre le changement de connectivité.

Physiquement, le changement de connectivité résultant de la reconnexion magnétique n'est possible que pour un plasma magnétisé et à de petites échelles spatiales, inférieures aux rayon de gyration des particules chargées. Dans cette situation, le plasma et le champ magnétique sont découplés (trop loin et le théorème du gel n'est plus valide), c'est ce qui permet aux lignes de champ de perdre leur identité et de pouvoir localement changer de direction.

L'équation d'induction est l'équation qui définit l'évolution du champ magnétique. En exprimant l'équations de Faraday, 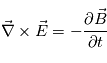$\vec \nabla \times \vec E =-\frac{\partial \vec B}{\partial t}$ , en utilisant l'équation de Maxwell 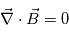$\vec \nabla \cdot \vec B =0$ et la loi d'Ohm non généralisé : 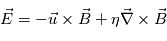$\vec E = -\vec u \times \vec B +\eta \vec \nabla \times \vec B$ , on obtient l'expression de l'équation d'induction : 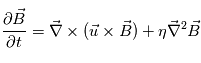$\frac{\partial \vec B}{\partial t}= \vec \nabla \times (\vec u \times \vec B)+ \eta \vec 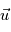\nabla^2 \vec B$ . Avec $\vec u$ la vitesse du plasma et 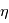$\eta$ la resistivité électrique du milieu. Le premier terme est le terme d'advection et le second terme est le terme dissipatif.

Le régime physique d'un plasma magnétisé est défini par son nombre de Reynolds magnétique qui est le rapport entre le terme dissipatif et le terme d'advection, 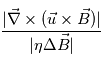$\frac{|\vec{\nabla}\times(\vec{u} \times \vec{B})|}{|\eta \Delta \vec B|}$ . La couronne solaire étant un très bon conducteur, la resistivité électrique 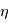$\eta$ est petite et le reynolds magnétique est alors >> 1 : le terme d'avection domine. La reconnexion magnétique se développe lorsque le terme dissipatif est du même ordre de grandeur que le terme d'advection du champ magnétique. En explicitant le nombre de Reynolds on obtient : 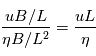$\frac{uB/L}{\eta B/ L^2}=\frac{uL}{\eta}$ . u est la vitesse caracteristique du plasma , L la longueur caracteristique de la region de dissipation et 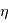$\eta$ la resistivité électrique du milieu. Si L devient très petit, le terme d'advection diminue et devient comparable au terme dissipatif. Dans la couronne solaire, le mécanisme de reconnexion magnétique se developpera aux petites échelles (L petit).

Pour que le changement de connectivité opère dans les régions de diffusion, il faut la présence d'un champ électrique parallèle au champ magnétique. C'est cette composante parallèle qui permet de briser le gel magnétique et de conduire au mouvement propre des lignes de champ magnétique. D'apres la loi d'Ohm non-généralisée, le terme 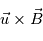$\vec u \times \vec B$ exprime le champ életrique crée par les déplacements du plasma magnétisé à une vitesse u. On peut montrer que le champ électrique parallele ne provient que du rotationnel du champ magnétique. 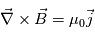La création d'un champ électrique s'accompagne de la formation d'une nappe de courant (loi de Maxwell-Ampère : $\vec \nabla \times \vec B = \mu_0 \vec j$ ).

Les configurations magnétiques des régions actives sont généralement multi-polaires, ce qui permet d'avoir des zones particulières ou le champ magnétique s'inverse rapidement. Ces zones sont généralement associées à une discontinuité du champ magnétique qui constitue des sites préférentiels pour le développement de la reconnexion magnétique.

Exercice

Question 1)

Bien que la reconnexion magnétique fasse appelle à des notions compliqués, on peut tout de même se faire une idée du principe en posant le problème le plus simplement possible. Soit un champ magnétique 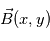$\vec B(x,y)$ distribué comme le montre le schéma (a ajouter)en coordonnées cartesienne. On suppose alors aucun mouvement de plasma, i.e., 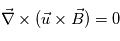$\vec \nabla \times(\vec u \times \vec B)=0$ . 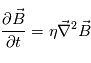L'équation d'induction est alors réduite à $\frac{\partial \vec B}{\partial t}= \eta \vec \nabla ^2 \vec B$ . Expliciter cette equation pour le champ magnetique donne ci-dessus :

Question 2)

A partir du schema ci-contre, trace l'evolution de bx et by en fonction de y. En utilisant ces profiles , evaluez le signe de leur dérivée seconde :

Question 3)

En deduire l'evolution au cours du temps des composante de bx et by. En conclure comment cela modifie les lignes de champ sur le schema.