Le noyau

Le noyau est le coeur du Soleil qui s'étend du centre à 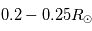$0.2-0.25 R_\odot$ et contient 60% de masse solaire. C'est dans cette région où est produite la majorité de l'énergie solaire rayonnée par la surface. Cette énergie est générée par les réactions de fusion nucléaires de l'hydrogène. En effet, la compression gravitationnelle dans cette région est telle que la densité est de 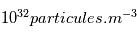$10^{32} particules.m^{-3}$ (la densité de l'atmosphère terrestre est de 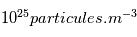$10^{25} particules.m^{-3}$ ) et la température atteint 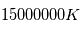15 000 000 K . Pour l'hydrogène, ces conditions impliquent que l'énergie cinétique du à lagitation thermiquedu plasma est supérieure à la repulsion coulombienne présente lorsque 2 particules de même charge se rapprochent.

La chaine de réaction nucléaire "PP1" au coeur du Soleil conduit à la fusion de 4 hydrogene en un atome d'Hélium et est la plus énergétique :

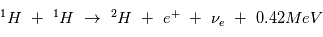
$^1H~+~^1H~\rightarrow ~^2H~+~e^+~+~\nu_e~+~0.42MeV$

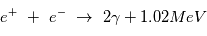
$e^+~+~e^-~\rightarrow~ 2\gamma+1.02MeV$

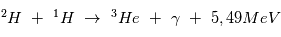
$^2H~+~^1H~\rightarrow~^3He~+~\gamma~+~5,49MeV$

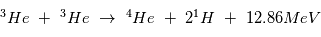
$^3He~+~^3He~\rightarrow~^4He~+~2^1H~+~12.86MeV$

Température de fusion au coeur du Soleil

Question 1)

Determiner la temperature minimale nécessaire pour que les processus de fusion se mettent en place. L'énergie thermique d'un gaz de densité n est : 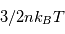3/2 n k_B T et l'energie coulombienne est 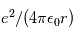$e^2/(4\pi \epsilon_0 r)$ où r est la distance entre les deux noyau et doit etre inférieure à 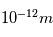$10^{-12}m$ , e est la charge d'un électron en coulomb 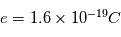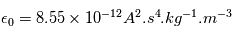$e=1.6\times10^{-19}C$ , $\epsilon_0=8.55\times 10^{-12} A^2.s^4.kg^{-1}.m^{-3}$ est la permettivité électrique du vide, 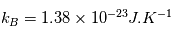$k_B=1.38\times10^{-23} J.K^{-1}$ est la constante de Boltzmann.

Energie de la fusion thermonucléaire

La chaine de réaction nucléaire PP1 décrite dans le cours peut se résumer à la fusion de 4 atomes d'hydrogène pour former un atome d'Helium. Lors de la fusion de 2 atomes, on peut calculer l'énergie libérée grâce à la relation d'Einstein : 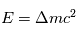$E=\Delta mc^2$ où m est la masse atomique en kg des éléments de la réaction, 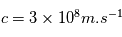$c=3 \times 10^8 m.s^{-1}$ est la vitesse de la lumière et l'énergie E est en Joule.

Nous rappelons que la masse atomique est la masse moyenne d'un atome. Cette masse se calcul à partir du nombre de particules du noyau et prend éalement en compte la présence d'isotopes (meme nombres de protons et d'électrons mais un nombre différent de neutrons). L'hydrogène 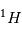^1H est formé d'un proton et d'un électron. Son isotope le Deuterium 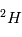^2H est consititué d'un proton, d'un neutron et d'un électron et le tritium 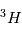^3 H = 1 proton, 2 neutrons et 1 electron. La masse atomique de l'hydrogène est donc 1,0079u.

Question 1)

Sachant que l'unité de masse atomique 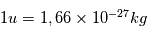$1u = 1,66\times 10^{-27}kg$ , calculez la masse atomique de 4 atomes d'hydrogène 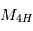$M_{4H}$ en kg?

Question 2)

La masse atomique d'un atome d'hélium est 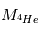$M_{^4 He}$ est 4.0026 u. En utilisant la relation masse-énergie d'einstein, calculer l'énergie libérée lors de la fusion de 4 atomes d'hydrogènes en un atome d'hélium.

Question 3)

Quelle est la fraction de masse d'hydrogène convertie en énergie ?

Question 4)

En considérant que seule 10% de la masse totale du Soleil est de l'hydrogène et peut être convertie en énergie, calculez l'énergie totale générée par fusion thermonucléaire.

Question 5)

L'énergie perdue par le Soleil par irradiation est 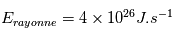$E_{rayonne}=4 \times 10^{26}J.s^{-1}$ . Estimez alors le temps de vie du Soleil pour consommer tout son hydrogène.