Fondamentaux de la propulsion

Auteur: Gary Quinsac

Action-réaction

Illustration du principe d'action-réaction. Le carburant éjecté propulse le véhicule dans la direction opposée.

Conversion d'énergie

Tous les types de systèmes de propulsion sont basés sur un processus de conversion d'énergie. Du carburant est libéré à grande vitesse (vitesse d'expulsion notée 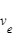v_e qui représente la vitesse relative entre le satellite et le carburant expulsé) avec une quantité de mouvement associée 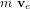$m \ \bold v_e$ , ce qui, par conservation de la quantité de mouvement, résulte en une quantité de mouvement opposée pour le véhicule. En partant de la troisième loi de Newton et en considérant que la vitesse d'expulsion est constante, on obtient : $\bold F = \dot m \bold v_e \ \textup{[N]}$ .

Incrément de vitesse

Ecrivons que la variation de la quantité de mouvement du satellite est opposée à la variation de la quantité de mouvement du carburant expulsé : 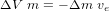$\Delta V \ m = -\Delta m \ v_e$

On peut directement en déduire la capacité d'incrément de vitesse total (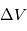 $\Delta V$ ) du satellite :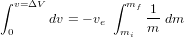 $\int_{0}^{v=\Delta V}{dv} = -v_e \ \int_{m_i}^{m_f}{\frac{1}{m} \ dm}$

On en déduit l'équation de Tsiolkovski : 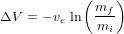$\Delta V = -v_e \ \textup{ln} \left( \frac{m_f}{m_i} \right)$

Manœuvres orbitales

Voici quelques exemples d'incréments de vitesse associés à des lancements et à des manœuvres orbitales issus de "Spacecraft propulsion - A brief introduction" par Peter Erichsen :

Incréments de vitesses associés à des manœuvres spatiales et de décollage
Manœuvre	ΔV typique [m/s]
Kourou → LEO (équatorial)	9300
Kourou → GTO	11443
Cap Canaveral → LEO (équatorial)	9500
Cap Canaveral → GEO	13600
LEO → GEO (changement d'inclinaison de 28°)	4260
GTO → GEO (changement d'inclinaison de 9°)	1500
GTO → GEO (changement d'inclinaison de 28°)	1800
Maintien à poste Nord/Sud	50 / an
Maintien à poste Est/Ouest	5 / an
LEO → Orbite de libération terrestre	3200
LEO → Orbite lunaire	3900
LEO → Orbite martienne	5700

Quantité de carburant

Si l'on veut déterminer la quantité de carburant nécessaire à la réalisation d'un manœuvre spatiale 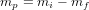m_p = m_i - m_f , il ne reste plus qu'à déplacer les termes de l'équation précédente afin d'obtenir :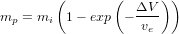 $m_p = m_i \left( 1 - exp \left( -\frac{\Delta V}{v_e} \right) \right)$

Impulsions

Nous pouvons maintenant définir de nouveaux termes. L'impulsion minimum (ou "impulse bit" en anglais, I_bit) est la plus petite modification de la quantité de mouvement permise par le système de propulsion. C'est un paramètre important lorsque l'on veut effectuer du contrôle fin de l'attitude et de l'orbite.
L'impulsion totale (I_tot) quant à elle représente la capacité de modification de la quantité de mouvement pour une quantité donnée de carburant : $I_{tot} = \int_{0}^{\tau}{F \ dt} = v_e \ \int_{0}^{m_p}{dm} = v_e \ m_p \ \textup{[N.s]}$ .
Il est essentiel de définir des paramètres permettant de comparer la performance des différents systèmes propulsifs. Le plus utilisé, l'impulsion spécifique (I_sp), peut être obtenue expérimentalement. Elle se définit comme l'impulsion délivrée par unité de poids de carburant : 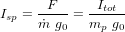$I_{sp} = \frac{F}{\dot m \ g_0} = \frac{I_{tot}}{m_p \ g_0}$ , avec 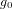le champ standard de la pesanteur (9,81 m.s^-2). Les impulsions spécifiques sont notées en secondes et parfois données en N.s.kg^-1, ce qui correspond à la formule précédente multipliée par l'accélération standard de la pesanteur, donnant l'impulsion délivrée par unité de masse.
Dans le but de déterminer la performance du système propulsif dans son ensemble, en incluant la masse de l'ensemble (l'électronique, le carburant et réservoir, l'alimentation) m_ps, on introduit l'impulsion spécifique du système, notée I_ssp : $I_{ssp} = \frac{I_{tot}}{m_{ps} \ g_0} \ \textup{[s]}$ .