Théorie simplifiée pour un analyseur magnétique

Auteur: Ronan Modolo

Concept physique sous-jacent

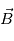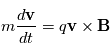
Lorsque les particules chargées entrent dans l'analyseur, elles se trouvent dans un milieu avec un champ magnétique uniforme et statique $\vec{B}$ . Le mouvement d'une particule non-relativiste dans un tel champ est donné par : $m\frac{d\mathbf{v}}{dt} = q\mathbf{v}\times\mathbf{B}$

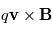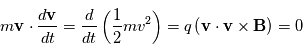
où $q\mathbf{v}\times\mathbf{B}$ est la force de Lorentz. En prenant le produit scalaire de l'équation ci-dessus avec le vecteur vitesse, nous obtenons $m\mathbf{v}\cdot\frac{d\mathbf{v}}{dt} = \frac{d}{dt}\left(\frac{1}{2}mv^2\right) = q\left(\mathbf{v}\cdot\mathbf{v}\times\mathbf{B}\right)=0$

Ce qui montre que l'énergie cinétique 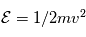$\mathcal{E}=1/2mv^2$ est une constante du mouvement. Pour déterminer la trajectoire il est avantageux de séparer les composantes des vitesses parallèle et perpendiculaire au champ magnétique. Soit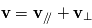 $\mathbf{v} = \mathbf{v}_{/\!/}+\mathbf{v}_\perp$

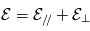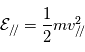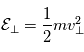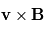L'énergie cinétique peut également se décomposer en une contribution parallèle et une autre perpendiculaire, $\mathcal{E} = \mathcal{E}_{/\!/}+\mathcal{E}_\perp$ où $\mathcal{E}_{/\!/}=\frac{1}{2}mv^2_{/\!/}$ et $\mathcal{E}_\perp=\frac{1}{2}mv^2_\perp$ . Comme la force $\mathbf{v}\times\mathbf{B}$ n'a pas de composante parallèle au champ magnétique, la composante parallèle de la vitesse est constante, donc la particule se déplace avec un vitesse constante le long du champ 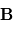$\mathbf{B}$ (sauf si 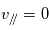$v_{/\!/} = 0$ ). 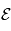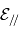Puisque $\mathcal{E}$ et $\mathcal{E}_{/\!/}$ sont constants alors 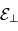$\mathcal{E}_\perp$ (et de ce fait 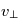$v_\perp$ ) sont également des constantes du mouvement.

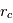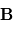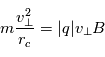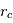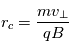
Le rayon de courbure r_c du mouvement de la particule dans le plan perpendiculaire à $\mathbf{B}$ peut s'écrire (en ignorant le signe) : $m\frac{v^2_\perp}{r_c} = |q|v_\perp B$ Le rayon r_c est souvent appelé le rayon de Larmor $r_c = \frac{mv_\perp}{qB}$

Si les ions entrant dans le secteur magnétique sont initialement passés par un analyseur électrostatique (seules les particules avec une énergie sélectionnée peuvent sortir de l'analyseur) alors les ions ont une énergie donnée 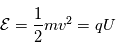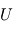$\mathcal{E}=\frac{1}{2}mv^2=qU$ ( est la tension d'accélération utilisé dans l'analyseur électrostatique). 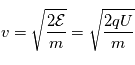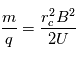La vitesse des ions vaut donc $v=\sqrt{\frac{2\mathcal{E}}{m}}=\sqrt{\frac{2qU}{m}}$ On obtient ainsi la mesure de masse sur charge : $\frac{m}{q} = \frac{r_c^2B^2}{2U}$

Les ions avec différents rapports de masse sur charge auront des rayons de Larmor différents et auront des zones d'impact sur le détecteur différentes.