 Objectifs
Objectifs
Les objectifs de ce chapitre sont, d'une part, de découvrir quelques méthodes de mesure in situ utilisées dans les missions d'explorations spatiales et, d'autre part, de comprendre sommairement le principe de fonctionnement de quelques uns des instruments qui permettent de caractériser le milieu plasma. Il ne s'agit donc pas de décrire en détail un instrument particulier, ou un jeu d'instruments, mais de présenter et assimiler les concepts physiques mis en jeu.
 Prérequis
Prérequis
Les concepts abordés dans ce chapitre font appel à des notions de :
- Electrostatique
- Magnétostatique
- Electromagnétisme
- Théorie cinétique des gaz
- Mécanique des fluides
- Mécanique classique
Plus particulièrement, ce chapitre est basé sur des techniques de mesures et de diagnostics utilisées en physique des plasmas. Bien que souhaitable, il n'est pas essentiel d'avoir suivi un cours de physique des plasmas pour comprendre ce chapitre.
 Un gaz ionisé rempli l'Univers
Un gaz ionisé rempli l'Univers
Il est souvent dit que l'univers est composé à 99% de plasma et que cet état constitue logiquement le quatrième état de la matière (solide, liquide, gazeux et plasma). Cela peut paraître surprenant car sur Terre, cet état n'existe que dans certains cas très précis. Il est possible de rencontrer cet état sous une forme naturelle dans les éclairs d'orage, les aurores boréales, ou bien sous une forme 'artificielle' (c'est-à-dire produite par l'homme) dans les tubes à décharges (lampes,...), les téléviseurs, dans les tokamaks pour la fusion nucléaire,...
En dehors de l'environnement terrestre, cet état constitue donc la majeure partie de l'univers visible et peut se rencontrer dans les étoiles, les nébuleuses, les pulsars et les systèmes planétaires. Pour comprendre la grande diversité des plasmas, il est fréquent de représenter leurs propriétés dans un diagramme densité-température (Fig). Nous remarquons que la densité peut varier de 20 ordres de grandeur tandis que la température peut s'échelonner sur 7 ordres de grandeurs, ce sont des variations extrêmement grandes.
Diversité des propriétés plasmas
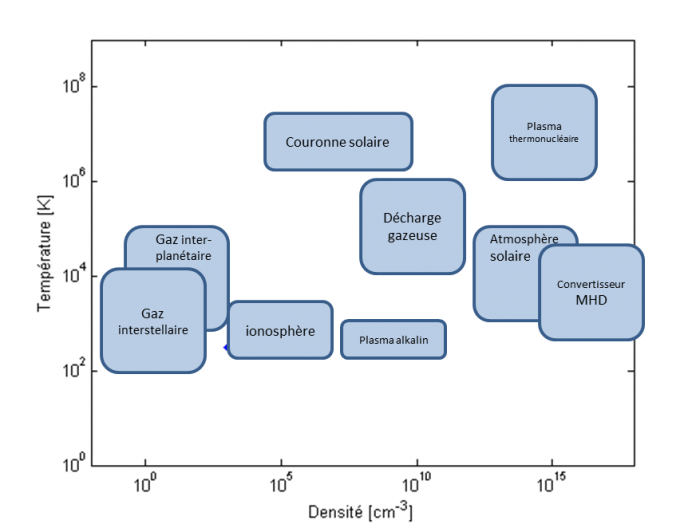
Diversité des plasmas naturels et artificiels que l'on peut rencontrer
 Mais qu'est-ce qu'un plasma ?
Mais qu'est-ce qu'un plasma ?
Considérons l'expérience suivante : une boîte contient un gaz mono-atomique (hydrogène par exemple) à température et pression atmosphérique constante. On suppose que les parois de la boîte sont parfaites et que les atomes frappant la paroi subissent une collision élastique et n'ont pas d'échange chimique avec la paroi. Le comportement de ce gaz obéit à la loi des gaz parfaits. Le comportement de ce gaz peut être décrit par la dynamique des fluides et des équations standard de la dynamique des gaz neutres de Navier-Stokes. Nous chauffons ce gaz à pression constante. Rappelons que la température est directement proportionnelle dans ce cas à l'énergie cinétique moyenne des particules constituant le gaz. A partir d'une température suffisamment élevée (de l'ordre de 1 million de K), les atomes sont ''ionisés''. Par conséquent les électrons sont littéralement arrachés de leur orbite dans l'atome et il est énergétiquement possible pour les électrons et les protons d'exister sous la forme de deux fluides distincts électriquement chargés. Notre gaz d'hydrogène a atteint l'état plasma.
Etat plasma
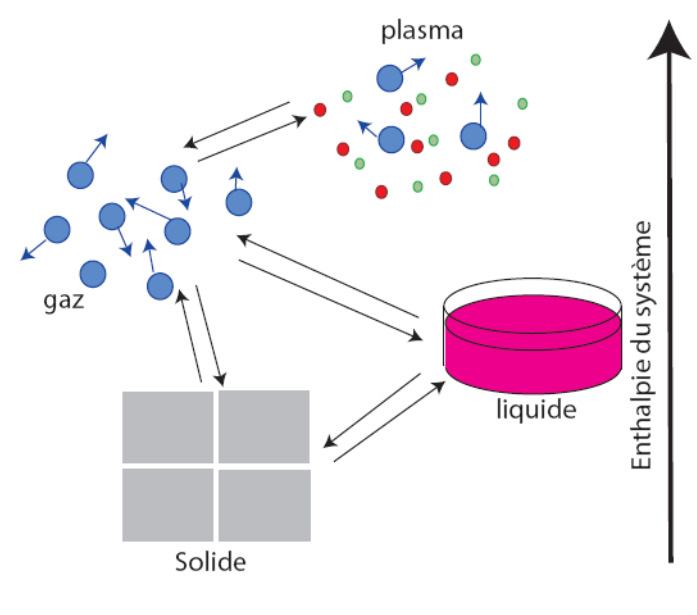
Représentation schématique des différents états de la matière
 Une description succincte des propriétés plasmas
Une description succincte des propriétés plasmas
Dans l'état plasma, la matière est composée, soit totalement soit partiellement, de particules chargées (électrons et ions) qui sont libres et non pas liées comme au sein d'atomes ou molécules. Cela découle simplement du fait que leur énergie cinétique liée au mouvement des particules est plus grande que l'énergie de liaison électrostatique de 13.6 eV ∼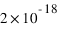 J (pour l'hydrogène). Gardons en tête que 1eV, ou un électron volt, est le travail fourni pour déplacer un électron au travers d'une différence de potentiel de un volt. C'est une unité d'énergie très utilisée en physique atomique et physique des plasmas.
J (pour l'hydrogène). Gardons en tête que 1eV, ou un électron volt, est le travail fourni pour déplacer un électron au travers d'une différence de potentiel de un volt. C'est une unité d'énergie très utilisée en physique atomique et physique des plasmas.
Du fait de leur charge électrique, les particules interagissent avec le champ électromagnétique, d'une part parce que le mouvement des particules chargées est régi par le champ magnétique, et d'autre part parce que l'ensemble des particules est lui-même source de champ, par la densité de charge et de courants que ces mouvements entraînent.
Parmi les nombreuses propriétés des plasmas, nous retiendrons d'une part qu'un plasma est globalement électriquement neutre mais que des écarts à la neutralité au niveau microspcopique, qui découle du fait que les particules chargées sont libres, sont susceptibles d'intervenir et d'autre part que les plasmas montrent des comportements collectifs, différents des gaz neutres, régis par les forces électromagnétiques. Ces effets collectifs sont plus importants que les forces Coulombiennes entre particules chargées.
Ainsi dans le cas des gaz, les ondes se propagent par l'action de collisions inter-moléculaires tandis que pour un plasma les ions peuvent se propager en l'absence de collisions au moyen de forces électromagnétiques qui agissent à distance sur les particules.
L'étude et le formalisme de la physique des plasmas s'appuient donc sur l'électromagnétisme pour décrire l'évolution du champ électromagnétique, la mécanique pour s'intéresser à la trajectoire de particules individuelles, la physique statistique qui permet de décrire l'évolution d'un grand nombre de particules et la mécanique des fluides pour comprendre le comportement global d'un fluide (électriquement chargé dans ce cas et donc les équations de la mécanique des fluides doivent être couplées avec les équations de Maxwell). La figure résume très schématiquement les interactions entre particules chargées et champ et les formalismes physique mis en jeu.
Relation Plasma
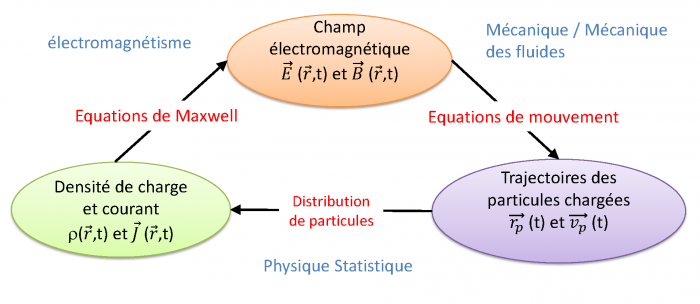
Représentation schématique entre le champ électromagnétique et les particules chargées.
Crédit :
R. Modolo
Quelques grandeurs caractéristiques
Une description plus détaillée de la physique des plasmas est disponible à la
page suivante. Dans ce chapitre nous nous interessons aux instruments et aux mesures qui permettent de caractériser ce milieu.
Certaines propriétés et caractéristiques de ce milieu sont également présentées telles que :
Nous ferons appel à ces notions dans ce chapitre.
 Quelles sont les quantités à mesurer ?
Quelles sont les quantités à mesurer ?
L'étude des plasmas nécessite d'avoir accès aux informations caractérisant le champ électromagnétique et les particules chargées dans la région considérée. Ces informations peuvent être obtenues à l'aide de différentes mesures et leurs instrumentations spécifiques. Comme nous l'avons montré en préambule, la diversité des plasmas est telle que des paramètres comme la densité ou la température varient sur plusieurs ordres de grandeurs. Il n'est de ce fait pas possible avec un unique instrument de couvrir l'ensemble des valeurs possibles.
Pour caractériser les environnements planétaires ionisés, il est nécessaire de décrire/caractériser les quantités suivantes :
- Les champs électrique et magnétique, ce sont des paramètres essentiels à mesurer. Les champs électrique et magnétique interviennent dans la dynamique des particules chargées via la force de Lorentz
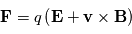 . Une description de l'effet du champ électromagnétique sur une particule chargée est décrit sur le site suivant
Ils sont également nécessaires pour caractériser les ondes dans les plasmas. Un exemple de propagation d'onde (caractéristique à la physique des plasmas) faisant intervenir le champ magnétique se trouve au lien suivant
NB : L'interprétation des résultats de l'appliquette requiert une assimiliation des concepts de physique plasmas (niveau M1)
.
. Une description de l'effet du champ électromagnétique sur une particule chargée est décrit sur le site suivant
Ils sont également nécessaires pour caractériser les ondes dans les plasmas. Un exemple de propagation d'onde (caractéristique à la physique des plasmas) faisant intervenir le champ magnétique se trouve au lien suivant
NB : L'interprétation des résultats de l'appliquette requiert une assimiliation des concepts de physique plasmas (niveau M1)
. - Le flux, l'énergie. Ces informations contribuent à l'étude de la dynamique du plasma dans la région explorée. Ces deux informations sont des mesures quasi-directes obtenues à partir des différents senseurs.
Le flux (des particules) consiste à déterminer le nombre de particules qui traversent une unité de surface par unité de temps, cela diffère du flux (magnétique) que nous avons introduit dans un chapitre suivant.
L'énergie est directement liée à la vitesse des particules (la vitesse dirigée et la vitesse thermique, i.e. la vitesse liée à l'agitation thermique)
- Fonction de distribution et moments. Pour un plasma constitué d'électrons et de différents types d'ions, il est nécessaire de définir la densité pour chacune des espèces et on utilise pour cela une approche statistique. Il est commode de représenter le comportement du plasma par une fonction de distribution
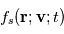 dont l'évolution (en temps et en espace) caractérisera la dynamique de chaque espèce
dont l'évolution (en temps et en espace) caractérisera la dynamique de chaque espèce 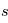 du plasma. La température des particules de l'espèce considérée est directement proportionnelle à l'énergie cinétique moyenne liée au mouvement aléatoire des particules. A l'équilibre thermique la fonction de distribution de vitesses des particules (de l'espèce considérée) est donnée par une distribution de vitesses de Maxwell-Boltzmann (appelé Maxwellienne, comme pour les gaz neutres).
Dans un grand nombre de cas l'analyse et l'interprétation des mesures plasmas requièrent la connaissance des moments de la fonction de distribution (la densité est le pemier moment de la fonction de distribution).
Ainsi l'intégration sur l'espace des vitesses de la fonction de distribution permet d'obtenir la densité de l'espèce considérée
du plasma. La température des particules de l'espèce considérée est directement proportionnelle à l'énergie cinétique moyenne liée au mouvement aléatoire des particules. A l'équilibre thermique la fonction de distribution de vitesses des particules (de l'espèce considérée) est donnée par une distribution de vitesses de Maxwell-Boltzmann (appelé Maxwellienne, comme pour les gaz neutres).
Dans un grand nombre de cas l'analyse et l'interprétation des mesures plasmas requièrent la connaissance des moments de la fonction de distribution (la densité est le pemier moment de la fonction de distribution).
Ainsi l'intégration sur l'espace des vitesses de la fonction de distribution permet d'obtenir la densité de l'espèce considérée 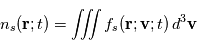 . Il s'agit du moment d'ordre 0.
Le moment d'ordre un donnera accès au flux
. Il s'agit du moment d'ordre 0.
Le moment d'ordre un donnera accès au flux 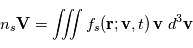 . Et ainsi de suite ...
. Et ainsi de suite ... - La composition ionique. La mesure de composition (et charge) du plasma est importante car elle donne une information sur l'origine (la source) du plasma. Il est ainsi possible de différencier les populations d'origine solaire (par exemple les
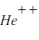 du vent solaire) et les ions
du vent solaire) et les ions 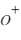 d'origine ionosphérique (issus directement ou indirectement de l'ionisation partielle de l'atmosphère de la planète).
Par ailleurs la composition a un impact direct sur la densité de masse du plasma. Ainsi même une faible abondance d'un ion lourd à une influence significative sur la densité de masse du plasma.
d'origine ionosphérique (issus directement ou indirectement de l'ionisation partielle de l'atmosphère de la planète).
Par ailleurs la composition a un impact direct sur la densité de masse du plasma. Ainsi même une faible abondance d'un ion lourd à une influence significative sur la densité de masse du plasma.
Nous nous limiterons à l'étude des plasmas naturels rencontrés dans le système solaire. Malgré ces considérations, aucun instrument ne peut couvrir ces larges gammes de densité, énergie, ... il existe donc de nombreux instruments qui permettent d'obtenir des mesures/observations sur une échelle de valeurs restreintes. Nous présentons uniquement un échantillon des possibles instruments embarqués sur les missions spatiales à titre d'illustration.
Nous présentons brièvement les instruments mentionnés à la page précédente et leurs principales caractéristiques.
- Mesures de champ magnétique
- Mesures particulaires
- Spectromètre électronique
- Spectromètre de masse ionique
- Sonde de Langmuir
La sonde spatiale Cassini et quelques-uns de ces instruments
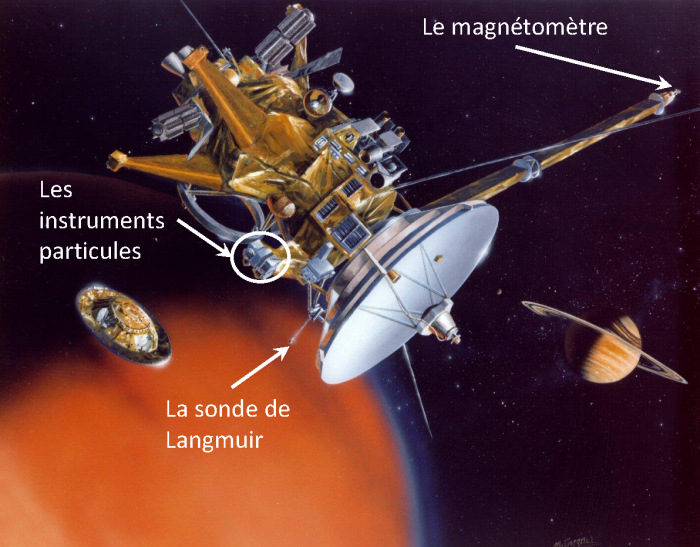
Vue d'artiste de la Sonde Cassini-Huygens
 Mesures particulaires
Mesures particulaires
En dépit du fait que les instruments particules utilisés en physique spatiale ont été construits avec diverses géométries et manipulant des combinaisons sur l'énergie des particules, l'état de charge, la masse des particules et l'analyse des espèces, il n'y a en fait que quelques techniques basiques qui permettent de sélectionner des particules avec des propriétés spécifiques. Ils peuvent faire appel à un champ électrostatique, ou à un champ magnétostatique, ou une combinaison de champ électrique et magnétique, ou en déterminant le temps de vol d'une particule sur une distance donnée... pour ne mentionner que ceux-ci.
Lors de la sélection d'un instrument pour une mission particulière ou si l'on souhaite comparer différents instruments plasmas, on regarde essentiellement quelques paramètres clefs. Ceux-ci sont :
- La gamme d'énergie (ou de vitesse) couverte par l'nstrument
- Le champ de vue de l'instrument (c'est-à-dire sa couverture angulaire)
- La résolution dans l'espace des vitesses (norme et direction) :
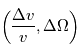
- Le facteur géométrique, qui détermine la sensibilité et la résolution temporelle de l'instrument
Nous nous intéresserons aux quelques instruments suivants :
 Mesure des électrons
Mesure des électrons
Les spectromètres électroniques permettent de déterminer la fonction de distribution des électrons des divers milieux traversés. Ces différentes régions se traduisent par des distributions de vitesse extrêmement variées. Ces instruments sont essentiellement constitués de plusieurs fenêtres d'entrées afin d'avoir une couverture angulaire la plus importante possible. Les particules chargées qui rentrent dans le système sont ensuite dirigées vers un analyseur électrostatique qui permet d'effectuer une sélection en énergie puis, en sortie de l'analyseur viennent impacter des galettes de microcanaux couplées à un système électronique qui permettent de compter les impacts et digitaliser les informations.
Ces instruments sont particulièrement utilisés dans les régions où le plasma est ''chaud'', c'est-à-dire dans le contexte des plasmas spatiaux, dont l'énergie est supérieure à une dizaine d'eV (jusqu'à plusieurs dizaine de keV).
 Mesure des ions
Mesure des ions
Tout comme les électrons, les spectromètres ioniques doivent permettre de caractériser les fonction de distribution de cette population du plasma et s'appuient également sur le principe d'analyseurs électrostatiques. Ces instruments doivent couvrir une grande échelle d'énergie et un grand champ de vue (idéalement 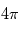 stéradians). Par ailleurs la caractérisation des ions nécessite de déterminer la masse de ceux-ci. Différents principes de spectrométrie de masse sont utilisés dans la physique des plasmas spatiaux et nous présenterons deux concepts.
stéradians). Par ailleurs la caractérisation des ions nécessite de déterminer la masse de ceux-ci. Différents principes de spectrométrie de masse sont utilisés dans la physique des plasmas spatiaux et nous présenterons deux concepts.
 Mesures des particules de basse énergie (Sonde de Langmuir)
Mesures des particules de basse énergie (Sonde de Langmuir)
Une sonde de Langmuir est une sonde électrostatique qui permet de mesurer, entre autre, la densité et la température électronique et le potentiel du plasma. Cela consiste en une électrode plongée dans le plasma. Pour l'exploration spatiale, cette électrode est située au bout d'un mât, à quelques mètres du corps du satellite. En faisant varier la tension appliquée à la sonde, un courant est collecté. L'analyse de cette réponse permet d'en déduire les propriétés du plasma (densité et température électronique, potentiel du satellite).
Cette technique est utilisée préférentiellement dans une région de plasma dense et ''froid'' ( > eV) tel que les régions ionosphériques.
 Quelques généralités sur le principe d'une sonde électrostatique
Quelques généralités sur le principe d'une sonde électrostatique
Les sondes électrostatiques utilisées pour les missions spatiales sont basées sur des techniques de laboratoire développées et présentées par Irving Langmuir et ses collègues au milieu des années 1920. Ce n'est seulement qu'à partir de la fin des années 1950 que ce type de technique a été utilisé sur des fusées et satellites pour mesurer la densité des ions et des électrons ionosphériques, la température électronique et le potentiel du satellite.
La technique des sondes de Langmuir consiste à mesurer le courant collecté par la sonde lorsque l'on fait varier la tension apliquéee à celle-ci. Une sonde électrostatique est une électrode conductrice de taille et forme appropriées qui est insérée dans le plasma (pour les plamas spatiaux la sonde se trouve sur au bout d'un mât du satellite). La tension sur l'électrode varie par rapport à une électrode de référence et le courant collecté est mesuré. L'analyse de la réponse ''tension-courant (U-I)'', appelé caractéristique va permettre de déterminer les propriétés du plasma : sa densité électronique 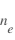 , sa température électronique
, sa température électronique 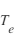 , la masse moyenne des ions
, la masse moyenne des ions 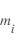 et la densité des ions
et la densité des ions 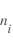 , ainsi que le potentiel du satellite.
, ainsi que le potentiel du satellite.
Une théorie simple de la sonde de Langmuir [Mott-Smith and Langmuir, 1926] montre que l'amplitude du courant électronique 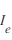 , est proportionnel à
, est proportionnel à 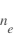 , et que l'amplitude du courant ionique
, et que l'amplitude du courant ionique 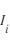 est proportionnel à
est proportionnel à 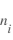 . Le courant pour des potentiels répulsifs est proportionnel à l'exponentielle de la tension divisée par la température :
. Le courant pour des potentiels répulsifs est proportionnel à l'exponentielle de la tension divisée par la température : 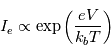
Caractéristique "tension-courant" d'une sonde électrostatique
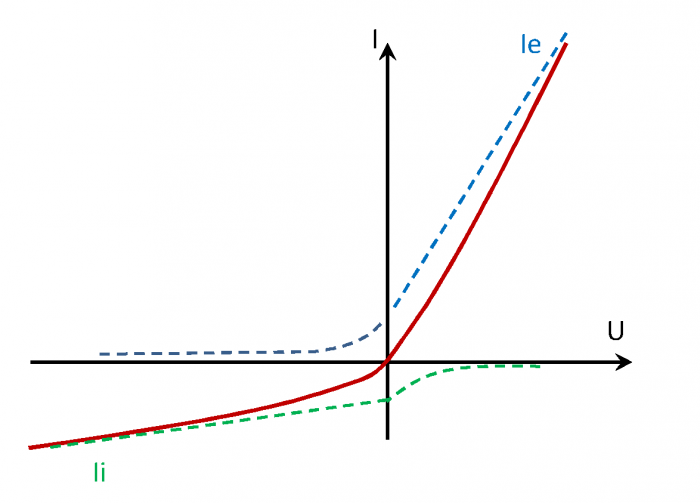
Représentation schématique d'une caractéristique U-I pour une sonde de Langmuir à symétrie sphérique (similaire à celle de Cassini). La courbe rouge indique le courant total collecté en fonction de la tension. Les courbes discontinues bleus et vertes indiquent les contribution respectives du courant électronique et du courant ionique.
On fait varier le potentiel appliqué à la sonde 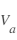 par rapport au satellite et on collecte le courant sur la sonde. Le courant
par rapport au satellite et on collecte le courant sur la sonde. Le courant 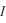 est la somme des courant ionique et électronique générés par les particules impactant la sonde. La figure de cette page illustre une représentation schématique d'un courant collecté par une sonde de Langmuir sphérique (celle de Cassini). Il est possible d'identifier différentes régions. Lorsque
est la somme des courant ionique et électronique générés par les particules impactant la sonde. La figure de cette page illustre une représentation schématique d'un courant collecté par une sonde de Langmuir sphérique (celle de Cassini). Il est possible d'identifier différentes régions. Lorsque 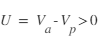 (
(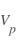 étant le potentiel du plasma) les électrons sont accélérés et les ions sont freinés. Dans le cas inverse (
étant le potentiel du plasma) les électrons sont accélérés et les ions sont freinés. Dans le cas inverse (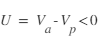 ) les électrons sont repoussés et les ions accélérés.
L'échantillonnage de la fonction de distribution des électrons en fonction du potentiel appliqué à la sonde est schématisé grâce à l'appliquette disponible à la page suivante.
) les électrons sont repoussés et les ions accélérés.
L'échantillonnage de la fonction de distribution des électrons en fonction du potentiel appliqué à la sonde est schématisé grâce à l'appliquette disponible à la page suivante.
Cette technique est une mesure active, c'est-à-dire qu'elle pertube le milieu qu'elle mesure. Ainsi l'insertion de la sonde va modifier le plasma. Lorsque la sonde n'est pas présente le plasma a localement une densité 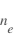 , une température
, une température 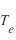 , une densité
, une densité 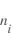 ,...
Lorsque la sonde est présente, la tension appliquée à la sonde va collecter les courants liés aux déplacement des charges électriques (ions et électrons). Du fait de la plus grande mobilité des électrons (moins massifs que les ions), les électrons vont impacter la sonde plus rapidement ce qui va créer une structure de potentiel autour de la sonde. Du coup un électron qui se trouve loin de la sonde et de sa structure de potentiel verra un potentiel différent que celui appliqué à la sonde à cause de cet écrantage. Cette région s'appelle la gaine et l'équilibre de charge entre ions et électrons est brisé.
,...
Lorsque la sonde est présente, la tension appliquée à la sonde va collecter les courants liés aux déplacement des charges électriques (ions et électrons). Du fait de la plus grande mobilité des électrons (moins massifs que les ions), les électrons vont impacter la sonde plus rapidement ce qui va créer une structure de potentiel autour de la sonde. Du coup un électron qui se trouve loin de la sonde et de sa structure de potentiel verra un potentiel différent que celui appliqué à la sonde à cause de cet écrantage. Cette région s'appelle la gaine et l'équilibre de charge entre ions et électrons est brisé.
 Introduction
Introduction
On appelle sonde électrostatique, ou sonde de Langmuir, un conducteur de petite dimension, plongé dans le plasma à étudier, polarisé électriquement et qui collecte les particules chargées du plasma. Au voisinage de la sonde se forme une gaine que l'on décrira rapidement par la suite.
La théorie classique des sondes électrostatiques repose sur les hypothèses suivantes :
- Il n'y a pas de collisions dans la gaine
- Les dimensions de la sonde sont petites devant le libre parcours moyens et devant les dimensions du plasma
- La sonde capte ou neutralise toutes les particules chargées qui arrivent à sa surface
- Le plasma est stationnaire, macroscopiquement neutre et équipotentiel au voisinage de la sonde
- La fonction de distribution des électrons est isotrope
 Distribution de Maxwell-Boltzmann
Distribution de Maxwell-Boltzmann
Les électrons ont une distribution des vitesses de Maxwell-Boltzmann (dite maxwellienne)
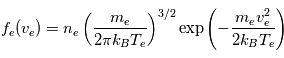
Le nombre d'électrons par unité de volume, dont le vecteur vitesse est compris entre 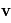 et
et 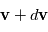 est ainsi égal à :
est ainsi égal à :
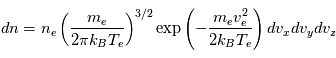
en système de coordonnées cartésiennes.
 En résumé ... et en savoir plus
En résumé ... et en savoir plus
L'analyse de la caractéristique tension-courant permet de déterminer quelques propriétés du plasma telles que la densité électronique et ionique, la température électronique ,...
En se limitant à la théorie la plus simple (sans prendre en compte les effets de gaine), il est possible de trouver des expressions théoriques ci-dessous :
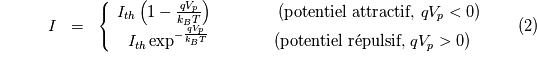
L'appliquette du lien suivant présente une observation de la sonde de Langmuir de Cassini (point rouge) et le résultat d'un ajustement d'une courbe théorique pour les paramètres d'entrées (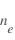 ,
, 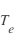 ...) à spécifier par l'utilisateur.
...) à spécifier par l'utilisateur.
 On ne vous a pas tout dit
On ne vous a pas tout dit
Dans le cas des sondes de Langmuir embarqués sur des missions spatiales, d'autres termes de courant contribuent au courant total. En particulier les photoélectrons du satellite ont une contribution non-négligeable dans le courant total. Ces photoélectrons sont les électrons arrachés du satellite (qui est composé de parties conductrices) lors de l'interaction entre le plasma et la sonde spatiale. Il existe d'autres contributions comme le courant des particules énergétiques ou le courant lié aux impacts de poussières (ou plasma poussiérieux) présentes dans l'espace.
 Un peu de lecture
Un peu de lecture
Pour approfondir, nous recommandons les lectures suivantes :
- Mott-Smith and Langmuir, Physical Review, 28, 727, 1926
- Laframboise J., Univ. Toronto Institue for Aerospace Studie, 1966
- Fahleson U, Space Science Reviews, 7, 238, 1967
- Chen F., ''Plasma diagnostic techniques'', Academic, New-York, 1965. Une note de lecture est disponible à l'adresse suivante
 Principe de fonctionement
Principe de fonctionement
Pour illustration nous prenons comme exemple le spectromètre électronique embarqué sur la mission Spatiale Cassini. Plus d'informations sont disponibles dans le papier de description instrumentale Young et al, Space Science Reviews, ..., 2004.
Ce spectromètre a été construit par le Mullard Space Science Laboratory, Angleterre.
Un schéma simplifié de l'instrument est présenté à la figure suivante. Cet instrument est essentiellement un analyseur électrostatique hémisphérique de type 'top-hat' (en référence au fait qu'une petite section d'analyseur se trouve placée au dessus des électrodes de déflection).
Schéma d'un spectromètre électronique
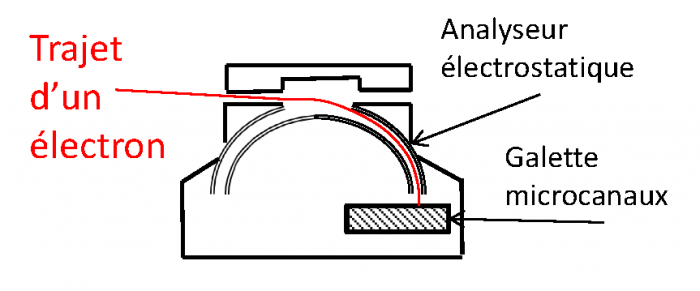
Représentation schématique du spectromètre électronique embarqué sur la mission Cassini et la trajectoire possible d'un électron en rouge.
Crédit :
Ce schéma est une version adaptée de la figure 3 de Young et al, SSR, 2004
Les électrons entrent dans le senseur via une des huit fenêtres d'entrées qui consiste en un baffle collimateur (les huit fenêtres définissent le champ de vue de l'instrument, c'est-à-dire sa couverture angulaire ). Ces électrons sont ensuite dirigés dans l'analyseur électrostatique jusqu'au détecteur, qui dans le cas du spectromètre électronique de Cassini sont des galettes micro-canaux. Ces galettes permettent la détection des particules chargées. La sélection en énergie s'effectue dans l'analyseur électrostatique. L'analyseur consiste en deux plaques/électrodes ayant pour l'une un potentiel nul et pour l'autre un potentiel que l'on applique. Le champ électrique 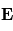 entre les deux électrodes exerce une force
entre les deux électrodes exerce une force 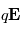 sur la particule qui va dévier la trajectoire lorsque celle-ci entre dans l'entrefer (espace entre les deux électrodes). Les particules atteignent les détecteur lorsque le rapport
sur la particule qui va dévier la trajectoire lorsque celle-ci entre dans l'entrefer (espace entre les deux électrodes). Les particules atteignent les détecteur lorsque le rapport 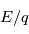 correspond à la force
correspond à la force 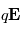 générée par le champ. En faisant varier le potentiel de l'électrode, il est possible de parcourir différentes gammes d'énergie. Les mesures présentent donc un spectre d'énergie. En analysant ce spectre, et en combinant les informations sur la couverture angulaire, il sera possible de reconstruire la fonction de distribution des électrons.
générée par le champ. En faisant varier le potentiel de l'électrode, il est possible de parcourir différentes gammes d'énergie. Les mesures présentent donc un spectre d'énergie. En analysant ce spectre, et en combinant les informations sur la couverture angulaire, il sera possible de reconstruire la fonction de distribution des électrons.
L'appliquette \ref{appliquette_analyseur_electrostatique} présente brièvement le mode de fonctionnement d'un analyseur électrostatique et la trajectoire d'un électron pour une énergie incidente fixée par l'utilisateur. Les potentiels des deux électrodes ont été fixés (valeurs non connues de l'utilisateur) et il s'agit de déterminer la bande passante en énergie.
Nous présentons deux cas simples d'analyseur électrostatique :
Les analyseurs sphériques ou hémisphériques sont des extensions naturelles de ces deux types d'analyseurs et ne présentent pas de concepts différents, seuls les calculs sont un peu plus compliqués.
Pour illustrer la théorie qui se cache derrière le fonctionnement d'un analyseur électrostatique nous prendrons le cas d'un analsyeur à électrodes parallèles (cf Figure). Notons que ce genre d'instrument n'a pas été embarqué à bord de missions spatiales et est utilisé juste dans le cadre d'explication du concept sur une géométrie simple.
Energie des particules et position du détecteur
Il est possible de décrire analytiquement la trajectoire d'une particule de charge 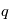 dans ce système. Nous présentons ici uniquement les résultats et les cacluls pourront être fait dans le cadre d'un exercice (cf exercice ).
Les équations paramétriques décrivant la trajectoire sont :
dans ce système. Nous présentons ici uniquement les résultats et les cacluls pourront être fait dans le cadre d'un exercice (cf exercice ).
Les équations paramétriques décrivant la trajectoire sont :
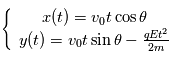
En notant 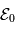 l'énergie cinétique initiale de la particule (à l'entrée du système), il est possible de relier la distance du détecteur (
l'énergie cinétique initiale de la particule (à l'entrée du système), il est possible de relier la distance du détecteur (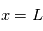 ) à l'énergie.
) à l'énergie.
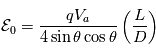
A partir d'un simple calcul d'incertitude il est possible de montrer que la résolution relative en énergie dépend de la position du détecteur et de sa largeur.
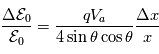
Ainsi en balayant le potentiel appliqué à l'électrode on pourra couvrir différentes gammes d'énergie et reconstruire la fonction de distribution en énergie.
 Configuration
Configuration
Un autre analyseur électrostatique simple a une géométrie cylindrique. Cet analyseur est constitué de deux secteurs cylindriques concentriques (cf Figure). Ce type d'analyseur a été utilisé lors de la mission spatiale Mariner 2. Cet analyseur a entre autre permis de fournir la confirmation expérimentale d'un vent solaire continu et de déterminer ses propriétés élémentaires [Snyder and Neugebauer, 1962].
Représentation schématique d'un analyseur à secteur cylindrique
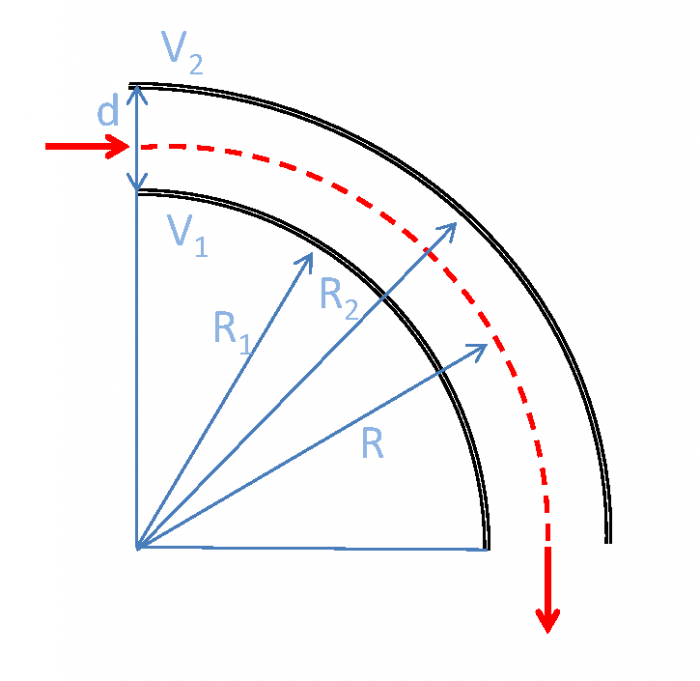
À cause de la géométrie cylindrique, seules les particules avec une vitesse parallèle à la normale du plan d'entrée de l'analyseur peuvent entrer dans celui-ci. Or avec une largeur 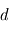 de l'entrefer, des particules avec une composante non nulle suivant le plan d'entrée de l'analyseur peuvent également se propager jusqu'à la sortie. Cela a pour conséquence d'augmenter la gamme d'énergie car les particules entrant dans l'analyseur avec un angle important par rapport à la normale peuvent être sélectionnées quand bien même leur énergie totale peut se trouver en dehors de la gamme d'énergie filtrée.
de l'entrefer, des particules avec une composante non nulle suivant le plan d'entrée de l'analyseur peuvent également se propager jusqu'à la sortie. Cela a pour conséquence d'augmenter la gamme d'énergie car les particules entrant dans l'analyseur avec un angle important par rapport à la normale peuvent être sélectionnées quand bien même leur énergie totale peut se trouver en dehors de la gamme d'énergie filtrée.
La spectrométrie de masse utilise le rapport masse sur charge (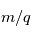 ) pour séparer les atomes et molécules ionisés. La spectrométrie de masse est l'une des techniques analytiques les plus sensibles et est fréquemment utilisée pour déterminer les propriétés du plasma. Le spectre de masse contient des informations sur la composition élémentaire (présence et nombre de certains éléments), l'abondance isotopique (la masse exacte) et la structure (les fragments).
) pour séparer les atomes et molécules ionisés. La spectrométrie de masse est l'une des techniques analytiques les plus sensibles et est fréquemment utilisée pour déterminer les propriétés du plasma. Le spectre de masse contient des informations sur la composition élémentaire (présence et nombre de certains éléments), l'abondance isotopique (la masse exacte) et la structure (les fragments).
Un spectromètre de masse se compose en deux parties, une source qui va ioniser le gaz et un analyseur qui va permettre la détermination des masses qui composent le mileu (en fait des rapport 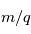 ). Dans le domaine spatial, le plasma est le milieu d'étude et la source d'ionisation n'est généralement pas nécessaire (sauf si on souhaite caractériser les atmosphères neutres planétaires). L'instrument se réduit donc à la partie analyseur.
). Dans le domaine spatial, le plasma est le milieu d'étude et la source d'ionisation n'est généralement pas nécessaire (sauf si on souhaite caractériser les atmosphères neutres planétaires). L'instrument se réduit donc à la partie analyseur.
Il existe différentes classes d'analyseur permettant de donner la masse des particules. Nous nous limiterons à une description succincte du fonctionnement de base de deux analyseurs :
 Description et principe de base
Description et principe de base
Un analyseur magnétique sépare les rapports 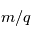 basés sur la déviation des trajectoires de particules ionisés dans un secteur magnétique. Dans le secteur magnétique, la trajectoire des ions est plane et est située dans le plan perpendiculaire à
basés sur la déviation des trajectoires de particules ionisés dans un secteur magnétique. Dans le secteur magnétique, la trajectoire des ions est plane et est située dans le plan perpendiculaire à 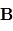 . La trajectoire est circulaire avec un rayon
. La trajectoire est circulaire avec un rayon 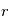 .
.
Connaissant la tension d'accélération des particules à l'entrée de l'analyseur, la zone d'impact sur le détecteur permet d'obtenir la masse de la particule.
Le schéma présente l'analyseur d'ions IMA (Ion Mass Anaylzer) embarqué sur les missions Mars Express et Venus Express.
On identifie un déflecteur électrostatique (partie du haut) qui va permettre d'avoir une acceptance angulaire des faisceaux d'entrée plus importante, un analyseur électrostatique de type ''top-Hat'' étudié précédemment, un analyseur magnétique où les trajectoires de différentes espèces (masses) ioniques illustrent les différentes zones d'impact du détecteur.
Le spectromètre de masse de Mars-Express / Venus-Express
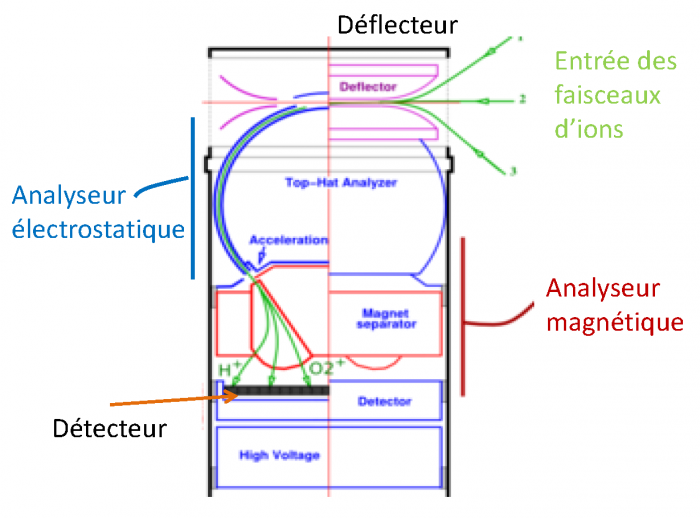
Représentation schématique du spectromètre de masse ionique de Mars-Express et Venus-Express.
Crédit :
Source : Thèse Claire Ferrier, 2009
 Principe de fonctionnement
Principe de fonctionnement
Un analyseur à temps de vol est également appelé ''Time of Flight'' ou ''TOF''. Cet analyseur repose sur le principe de détermination du temps de vol des particules qui entrent dans l'analyseur. Pour une particule à une énergie connue 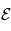 , on mesure le temps que la particule met pour effectuer la distance entre la source et le détecteur. Connaissant le temps de parcours et la distance parcourue, on en déduit la vitesse. Comme l'énergie de la particule est déterminé on peut en déduire sa masse.
, on mesure le temps que la particule met pour effectuer la distance entre la source et le détecteur. Connaissant le temps de parcours et la distance parcourue, on en déduit la vitesse. Comme l'énergie de la particule est déterminé on peut en déduire sa masse.
Par exemple pour une même énergie de départ 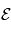 deux particules de masse
deux particules de masse 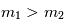 auront des vitesses telles que
auront des vitesses telles que 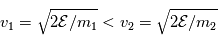 . C'est-à-dire que la vitesse de la particule légère (
. C'est-à-dire que la vitesse de la particule légère (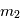 ) sera plus grande que la vitesse de la particule lourde (
) sera plus grande que la vitesse de la particule lourde (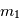 ). Comme les deux particules ont parcouru la même distance
). Comme les deux particules ont parcouru la même distance 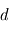 on trouve que le temps de parcours de la particule légère
on trouve que le temps de parcours de la particule légère 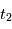 sera plus bref que celui de la particule lourde
sera plus bref que celui de la particule lourde 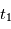 .
.
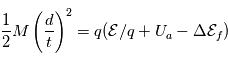 avec
avec 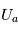 un potentiel de post-accélération et
un potentiel de post-accélération et 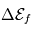 l'énergie perdue lors de collision à travers une feuille de carbone (cf ci-dessous).
Soit
l'énergie perdue lors de collision à travers une feuille de carbone (cf ci-dessous).
Soit
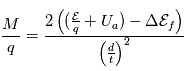
 Description du spectromètre de masse de Cassini
Description du spectromètre de masse de Cassini
Prenons comme illustration le spectromètre à temps de vol de l'instrument CAPS sur Cassini (cf figure). Dans ce schéma, tout comme celui de l'analyseur de Mars Express, les particules passent d'abord par un analyseur électrostatique type top hat avant de rentrer la partie de l'analyseur en masse. Cet analyseur en masse est représenté par la cavité se situant après l'analyseur électrostatique ou un champ électrique quasi-linéaire est présent. Un détecteur se trouvant au bas de l'instrument (ST) se trouve dans une région où le potentiel est proche de +15kV (les particules chargées négativement viendront principalement impacter ce détecteur), le détecteur se trouvant au dessus (LEF) est situé dans une région où le potentiel est proche de -15kV (seul les ions positifs peuvent impacter ce détecteur).
Analyseur à temps de vol de CAPS-CASSINI
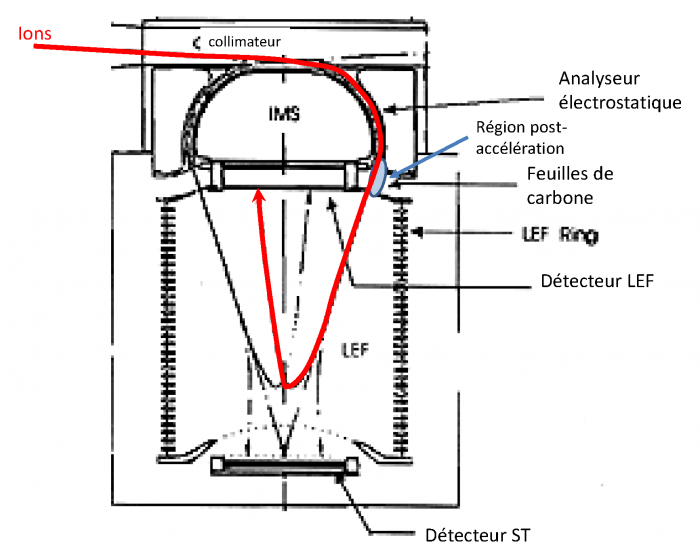
Représentation schématique du spectromètre de masse de type temps de vol de l'expérience Cassini CAPS. Le trajet d'un ion est représenté par la courbe rouge
Crédit :
NASA, image modifiée et commentée par R. Modolo
 Principe de fonctionnement du spectromètre TOF
Principe de fonctionnement du spectromètre TOF
Le principe de fonctionnement est le suivant :
- Les ions rentrent dans le collimateur du top hat et sont dirigés vers l'entrée de l'analyseur électrostatique
- Une tension est appliquée à l'électrode intérieure de l'analyseur électrostatique qui crée un champ électrique qui va modifier les trajectoires des particules. C'est la sélection en énergie : seules les particules autour d'une énergie donnée pourront ressortir de l'analyseur électrostatique. En sortie de l'analyseur, les ions sont accélérés par une tension de post-accélération (
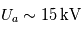 ).
).
- Les ions viennent impacter une feuille de carbone avec l'énergie
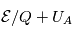 , où
, où 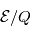 est l'énergie des particules en sortie de l'analyseur électrostatique.
est l'énergie des particules en sortie de l'analyseur électrostatique. - Les ions (atomiques et moléculaires) se fragmentent en particules plus élémentaires (électron, atome neutre, ion atomique de charge positive ou négative,...).
- Lors de l'impact sur la feuille de carbone, des électrons secondaires sont arrachés de celle-ci, attirés par le potentiel positif +15 kV ; ces électrons viendront impacter le détecteur ST. C'est le signal START du début de mesure du temps de vol.
- Lorsque des ions positifs sont arrachés, et s'ils sont une énergie
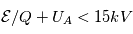 , ils viendront impacter le détecteur LEF et produiront un signal STOP. La différence de temps entre le signal de départ et le signal d'arrivée permettra d'en déduire le temps de vol. Dans ce cas de figure le champ électrostatique agit sur la trajectoire de la particule (
, ils viendront impacter le détecteur LEF et produiront un signal STOP. La différence de temps entre le signal de départ et le signal d'arrivée permettra d'en déduire le temps de vol. Dans ce cas de figure le champ électrostatique agit sur la trajectoire de la particule (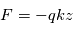 ) et l'équation de mouvement suivant la direction
) et l'équation de mouvement suivant la direction 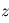 est celle d'un oscillateur harmonique. On en déduit le temps de vol tel que
est celle d'un oscillateur harmonique. On en déduit le temps de vol tel que 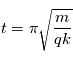 .
. - Si les ions en sortie de feuille de carbone ont une énergie supérieure à 15 kV alors le champ électrostatique ne fera que ralentir l'ion et il viendra impacter le détecteur ST.
- Les autres ions négatifs sortant de la feuille de carbone seront attirés par le potentiel +15 kV et impacteront le détecteur ST tandis que les neutres, qui sont insensibles au champ électrique, continueront leur trajectoire initiale et impacteront également le détecteur ST
On se place dans un cas de figure simple d'un analyseur à temps de vol linéaire (Wiley and McLaren, 1955).
Le montage est présenté à la figure suivante.
On applique une tension d'accélération connue. La vitesse de la particule est liée à cette tension d'accélération (l'énergie potentielle électrostatique est transformée en énergie cinétique)
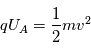 Dans la région de champ libre, l'énergie de la particule n'évolue pas. Le temps
Dans la région de champ libre, l'énergie de la particule n'évolue pas. Le temps  pour parcourir la distance
pour parcourir la distance 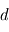 est lié à sa vitesse
est lié à sa vitesse 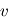 .
.
Soit
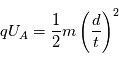 On en déduit le temps de vol
On en déduit le temps de vol
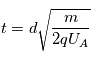
Schéma d'un analyseur à temps de vol linéaire
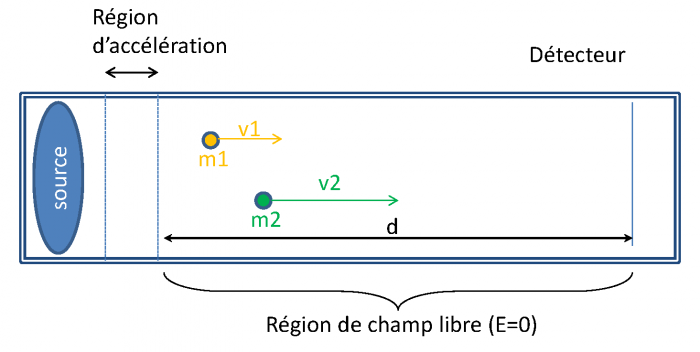
Représentation schématique d'un analyseur à temps de vol linéaire.
Crédit :
Reproduction simplifiée de Wiley and McLaren, 1955.
Le mouvement des particules chargées est contraint par le champ magnétique, de ce fait, une connaissance des variations spatiales et temporelles du champ magnétique est primordiale. Les magnétomètres ont été largement utilisés à bord de missions spatiales d'exploration terrestres et planétaires. Nous nous intéressons ici aux mesures de champ magnétique continu obtenu à l'aide d'un magnétomètre de type magnétomètre à vanne de flux, également appelé fluxgate. Les mesures des fluxgate peuvent également fournir des informations sur les ondes basses fréquences.
 Montage
Montage
Un fuxgate est donc constitué d'un tore en matériau ferromagnétique sur lequel on place deux bobinages :
- un bobinage d'excitation (appelée drive winding ou excitation coil)
- un bobinage de mesure (appelée sense winding ou pickup coil)
Une représentation schématique d'un fluxgate est illustrée sur la figure suivante.
Schéma d'un fluxgate
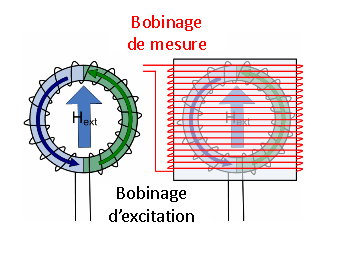
 Ce qu'il faut retenir
Ce qu'il faut retenir
Les magnétomètres à vannes de flux, ou fluxgate, utilisent les propriétés des matériaux ferromagnétiques pour mesurer un champ d'induction externe. Le système consiste en un tore ferromagnétique entouré d'un premier bobinage parcouru par un courant d'intensité sinusoïdale (ou triangulaire). Ce courant génère un champ magnétique qui va s'ajouter au champ externe à mesurer. De façon liée à la géométrie du système, une partie du champ généré va avoir une composante parallèle au champ externe, l'autre anti-parallèle. Cette différence de champ va provoquer une variation de flux magnétique et induira une tension induite dans un deuxième bobinage. Cette tension induite contient les harmoniques de la tension d'excitation. Le filtrage de la seconde harmonique permet de retrouver l'information sur le champ externe à mesurer.
 Un peu de lecture
Un peu de lecture
Pour approfondir le sujet nous recommandons les lectures suivantes :
- Primdahl F., J. Phys. E. Sci. Instrum. Vol 12, 1979
- Acuna M. H., Rev Sci. Inst. 73, 3717, 2002
- Mesure de champ magnétique (en anglais) par Steven A Macintyre
- Moutoussamy J., Thèse, 2009
- Leroy P., Thèse, 2007
- Coillot C., HDR, 2012
- Rhouni A., Thèse, 2012
Les questions suivantes portent sur des questions en lien direct avec le cours. La solution ne nécessite que quelques lignes de calcul si elle ne se trouve pas déjà exprimée dans les pages du chapitre.
 Ecrantage dans un plasma
Ecrantage dans un plasma
Difficulté : ☆☆
On considère une charge test 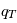 située en un point O placée dans un plasma dont le densité particulaire, à la distance r de O, peut s'écrire
pour les ions :
située en un point O placée dans un plasma dont le densité particulaire, à la distance r de O, peut s'écrire
pour les ions :
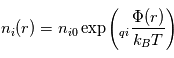
et pour les électrons :
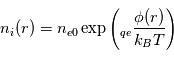
où 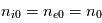 (hypothèse de quasi-neutralité du plasma) est la densité particulaire moyenne,
(hypothèse de quasi-neutralité du plasma) est la densité particulaire moyenne, 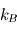 est la constante de Boltzmann,
est la constante de Boltzmann, 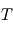 est la température,
est la température, 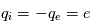 est la chage des particules, et
est la chage des particules, et 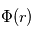 est le potentiel qui règne à la distance
est le potentiel qui règne à la distance 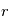 de O.
de O.
Question 1)
Déterminer la densité voulumique 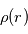
Question 2)
En appliquant le théorème de Gauss entre deux sphères de rayons 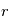 et
et 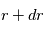 , donner l'équation satisfaite par le champ électrostatique. En déduire une équation différentielle de deuxième ordre sur le potentiel
, donner l'équation satisfaite par le champ électrostatique. En déduire une équation différentielle de deuxième ordre sur le potentiel 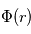
Pensez à utliser la symétrie du problème.
La dérivée seconde de la composante radiale d'une fonction f(r) s'écrit :
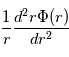
Question 3)
On se place dans le cas de haute températures 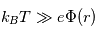 . Simplifier l'équation précédente et la résoudre.
La solution approche le potentiel de Coulomb de
. Simplifier l'équation précédente et la résoudre.
La solution approche le potentiel de Coulomb de 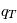 quand
quand 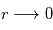 et reste finie à toutes les distances.
et reste finie à toutes les distances.
On pourra poser que 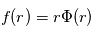 pour résoudre plus facilement l'équation différentielle
pour résoudre plus facilement l'équation différentielle
 Quantité macroscopique
Quantité macroscopique
Difficulté : ☆
On considère une fonction de distribution de vitesse Maxwellienne de la forme :
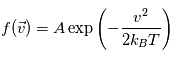
avec 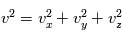 ,
, 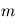 la masse des particules,
la masse des particules, 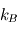 la constante de Boltzamnn,
la constante de Boltzamnn, 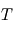 la température et
la température et 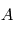 une quantité réelle.
une quantité réelle.
Question 1)
Déterminer 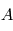 telle que
telle que
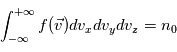
où 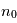 est la densité des particules
est la densité des particules
Question 2)
Montrer que :
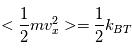
On rappelle que 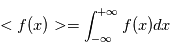
Question 3)
Montrer que :
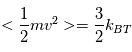
Question 4)
Comment représenter mathématiquement une distribution de vistesse Maxwellienne avec une vitesse de dérive 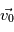
Question 5)
Déterminer la distribution en énergie de la fonction de distribution de vitesse précédente
Poser 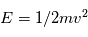 et effectuer le changement de variable
et effectuer le changement de variable 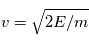
Auteur: R. Modolo
 Mouvement d'une particule chargée dans un champ électromagnétique
Mouvement d'une particule chargée dans un champ électromagnétique
Difficulté : ☆
Temps : 15 min
On considère une particule de charge électrique q et de masse m plongée dans un champ magnétique uniforme 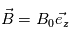 . On cherche à déterminer le mouvement de la particule dans ce champ magnétique. On se place dans un repère cartésien orthonormé
. On cherche à déterminer le mouvement de la particule dans ce champ magnétique. On se place dans un repère cartésien orthonormé 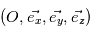 . A t=0 la position de la particule est telle que
. A t=0 la position de la particule est telle que 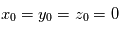 et sa vitesse intiale est définie par
et sa vitesse intiale est définie par 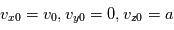 .
.
Question 1)
Dans un premier temps on considère que le champ électrique est nul. Ecrire les équations de mouvement de la particule
Appliquer le principe fondamentale de la dynamique
Question 2)
Résoudre ces équations en utilisant les conditions initiales
Projeter suivant les axes du système et introduire une nouvelle variable 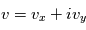
Question 3)
Quelle est la trajectoire de cette particule ? La tracer.
Question 4)
On considère maintenant que la particule est toujours plangé dans le magnétique 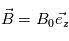 mais qu'un champ électrique est désormais présent tel que
mais qu'un champ électrique est désormais présent tel que 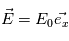 . Comment la trajectoire est-elle modifiée ?
. Comment la trajectoire est-elle modifiée ?
Effectuer le changement de variable 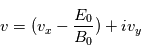
Auteur: R. Modolo
 Champ magnétique créé par une bobine torique
Champ magnétique créé par une bobine torique
Difficulté : ☆
Temps : 15 min
Soit une bobine sphérique constituée d'un enroulement de N spires circulaires de rayon r parcourue par le même courant I. Ces N spires entourent réglièrement un tore de rayon R de section circulaire de rayon r<R.
Question 1)
Montrer que le champ magnétique est nul en dehors du tore et déterminer son expression à l'intérieur de celui-ci en fonction de la distance 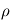 à l'axe du tore.
à l'axe du tore.
Déterminer les invariances de B et utiliser le théorème d'Ampère 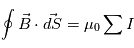
Question 2)
Déterminer les valeurs extrêmes du champ magnétique pour N=500, I=0.1 mA, R=10cm et r=1cm.
Quel courant devrait-on faire passer dans un fil rectiligne unique pour obtenir le même champ à la même distance ?
Les valeurs extrèmes sont obtenues pour 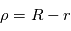 et
et 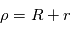
Auteur: Ronan Modolo
 Etude d'un analyseur électrostatique à plaque parallèle
Etude d'un analyseur électrostatique à plaque parallèle
Difficulté : ☆
On considère le montage de la figure suivante. Une particule chargée de charge q (>0) entre dans le dispositif en (0,0) avec une vitesse 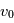 , et avec un angle
, et avec un angle 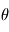 entre le vecteur vitesse de la particule et l'axe x du montage. On cherche à caractériser le mouvement de cetteparticule chargée.
entre le vecteur vitesse de la particule et l'axe x du montage. On cherche à caractériser le mouvement de cetteparticule chargée.
Question 1)
Dans quelle sens est dirigée le champ électrique E qui apparait entre les deux plaques parallèles? Quelle relation a-t-on entre le potentiel Va et le champ électrique E ?
Question 2)
Déterminer les conditions initiales du problème pour la position et la vitesse de la particule.
Projeter suivant les axes x et y.
Question 3)
Déterminer les forces qui s'appliquent à cette particule et simplifier éventuellement le problème.
On pourra prendre les valeurs numériques suivantes : 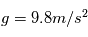 ,
, 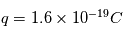 ,
, 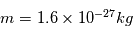 ,
, 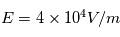
Comparer le poids a la force électrostatique
Question 4)
Déterminer l'équation paramétrique de la trajectoire (x(t), y(t)).
Appliquer le principe fondamentale de la dynamique puis projeter suivant les axes x et y.
Question 5)
Dans l'hypothèse où la particule n'atteint pas la plaque supérieure, déterminer le temps auquel la particule chargée atteint le sommet de sa trajectoire puis sa coordonée y.
Le sommet de la trajectoire est atteint lorsque 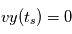
Question 6)
Au bout de combien de teps la particule impacte-t-elle la plaque du bas ? A quelle distance de la position d'entrée ?
L'objectif de se projet est de se familiariser avec les expériences et les mesures spatiales. Pour cela nous prenons comme contexte la mission Cassini et nous nous intéressons à un survol de Titan (T21) ayant eu lieu le 12/12/2006. Une vue d'ensemble des observations obtenus au cours de ce survol est présenté à la figure ci-joint.
Survol T21 de Titan par la sonde Cassini.
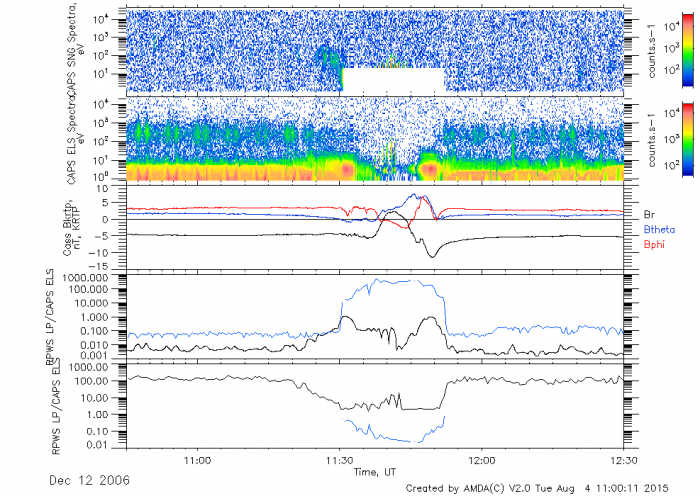
Le premier panneau présente les observations du spectromètre de masse ionique (CAPS-IMS), le second les observations du spectromètre électronique (CAPS-ELS), le troisième panneau montre les observations du champ magnétique (MAG) tandis que les quatrième et cinquième panneau sont la densité et la température électronique. Les informations déduites de la sonde de Langmuir (RPW-LP) sont indiqués en bleu et les courbes noirs représentent les informations déduites du spectromètre électronique.
Crédit :
La figure a été réalisé à partir d'
AMDA. Les données sont en accès libre et archivé à la base du
"Planetary Data System" de la NASA.
Les données que l'on utilise pour ce projet sont celles mesurées par la sonde de Langmuir (RPWS-LP) et celles du spectromètre électronique (CAPS-ELS)
- Pour la sonde de Langmuir : Le fichier de données est accessible via l'URL suivante
- Pour le spectromètre électronique : Le fichier pré-traité (par rapport aux données du PDS qui sont des données brutes nous avons étalonné les mesures) est accessible via l'URL suivante
Une fois les fichiers de données téléchargées et lues, vous devez obtenir des graphiques similaires à ceux de cette page.
Donnees_LP
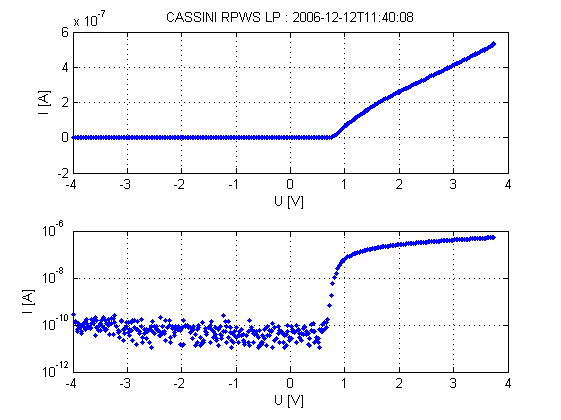
Données de la sonde de Langmuir tension-intensité représenté en échelle linéaire (panneau du haut) et échelle logarithmique (panneau du bas).
CASSINI 2006/12/12 à 11:40:00
Crédit :
Les données sont extraites du NASA Planetary Data System.
Données CAPS ELS
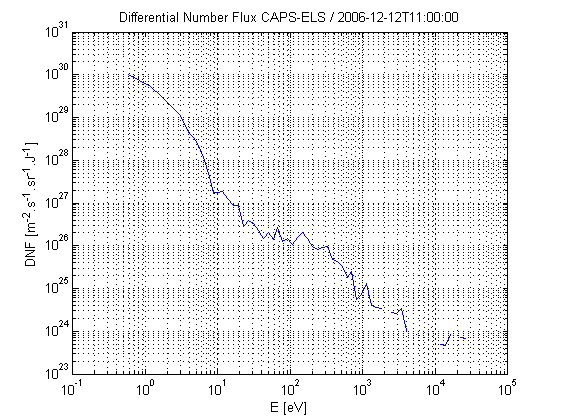
Données du spectromètre électronique CAPS ELS. Les données représente un flux différentiel. (CASSINI 2006/12/12 à 11:00:00)
Crédit :
Les données sont extraites du PDS puis retravaillées pour être converties en unité physique.
-------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------
ACCES AU PLAN DES CHAPITRES
 Objectifs
Objectifs Prérequis
Prérequis

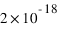 J (pour l'hydrogène). Gardons en tête que 1eV, ou un électron volt, est le travail fourni pour déplacer un électron au travers d'une différence de potentiel de un volt. C'est une unité d'énergie très utilisée en physique atomique et physique des plasmas.
J (pour l'hydrogène). Gardons en tête que 1eV, ou un électron volt, est le travail fourni pour déplacer un électron au travers d'une différence de potentiel de un volt. C'est une unité d'énergie très utilisée en physique atomique et physique des plasmas.

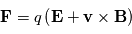 . Une description de l'effet du champ électromagnétique sur une particule chargée est décrit sur le site
. Une description de l'effet du champ électromagnétique sur une particule chargée est décrit sur le site 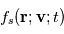 dont l'évolution (en temps et en espace) caractérisera la dynamique de chaque espèce
dont l'évolution (en temps et en espace) caractérisera la dynamique de chaque espèce 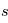 du plasma. La température des particules de l'espèce considérée est directement proportionnelle à l'énergie cinétique moyenne liée au mouvement aléatoire des particules. A l'équilibre thermique la fonction de distribution de vitesses des particules (de l'espèce considérée) est donnée par une distribution de vitesses de Maxwell-Boltzmann (appelé Maxwellienne, comme pour les gaz neutres).
Dans un grand nombre de cas l'analyse et l'interprétation des mesures plasmas requièrent la connaissance des moments de la fonction de distribution (la densité est le pemier moment de la fonction de distribution).
Ainsi l'intégration sur l'espace des vitesses de la fonction de distribution permet d'obtenir la densité de l'espèce considérée
du plasma. La température des particules de l'espèce considérée est directement proportionnelle à l'énergie cinétique moyenne liée au mouvement aléatoire des particules. A l'équilibre thermique la fonction de distribution de vitesses des particules (de l'espèce considérée) est donnée par une distribution de vitesses de Maxwell-Boltzmann (appelé Maxwellienne, comme pour les gaz neutres).
Dans un grand nombre de cas l'analyse et l'interprétation des mesures plasmas requièrent la connaissance des moments de la fonction de distribution (la densité est le pemier moment de la fonction de distribution).
Ainsi l'intégration sur l'espace des vitesses de la fonction de distribution permet d'obtenir la densité de l'espèce considérée 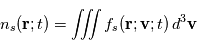 . Il s'agit du moment d'ordre 0.
Le moment d'ordre un donnera accès au flux
. Il s'agit du moment d'ordre 0.
Le moment d'ordre un donnera accès au flux 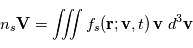 . Et ainsi de suite ...
. Et ainsi de suite ...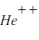 du vent solaire) et les ions
du vent solaire) et les ions 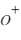 d'origine ionosphérique (issus directement ou indirectement de l'ionisation partielle de l'atmosphère de la planète).
Par ailleurs la composition a un impact direct sur la densité de masse du plasma. Ainsi même une faible abondance d'un ion lourd à une influence significative sur la densité de masse du plasma.
d'origine ionosphérique (issus directement ou indirectement de l'ionisation partielle de l'atmosphère de la planète).
Par ailleurs la composition a un impact direct sur la densité de masse du plasma. Ainsi même une faible abondance d'un ion lourd à une influence significative sur la densité de masse du plasma.
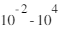 nT
nT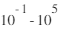 nT
nT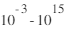 nT
nT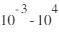
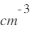
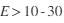 eV)
eV)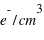 à
à 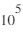
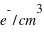
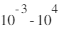
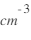 Masse: m/q = 1
Masse: m/q = 1 
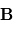 (mesure scalaire) mais également les composantes
(mesure scalaire) mais également les composantes 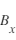 ,
, 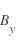 et
et 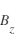 du champ magnétique (mesure vectorielle).
On distinguera les magnétomètres continus (type fluxgate) qui sont sensibles aux bandes passantes 0-60Hz des magnétomètres alternatifs (type search-coil) qui sont eux sensibles aux fréquences plus élevées ( > 100 Hz). Ces derniers sont essentiellement utilisés pour l'étude des ondes.
du champ magnétique (mesure vectorielle).
On distinguera les magnétomètres continus (type fluxgate) qui sont sensibles aux bandes passantes 0-60Hz des magnétomètres alternatifs (type search-coil) qui sont eux sensibles aux fréquences plus élevées ( > 100 Hz). Ces derniers sont essentiellement utilisés pour l'étude des ondes.
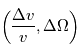
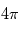 stéradians). Par ailleurs la caractérisation des ions nécessite de déterminer la masse de ceux-ci. Différents principes de spectrométrie de masse sont utilisés dans la physique des plasmas spatiaux et nous présenterons deux concepts.
stéradians). Par ailleurs la caractérisation des ions nécessite de déterminer la masse de ceux-ci. Différents principes de spectrométrie de masse sont utilisés dans la physique des plasmas spatiaux et nous présenterons deux concepts.
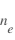 , sa température électronique
, sa température électronique 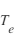 , la masse moyenne des ions
, la masse moyenne des ions 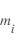 et la densité des ions
et la densité des ions 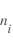 , ainsi que le potentiel du satellite.
, ainsi que le potentiel du satellite.
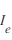 , est proportionnel à
, est proportionnel à 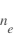 , et que l'amplitude du courant ionique
, et que l'amplitude du courant ionique 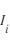 est proportionnel à
est proportionnel à 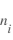 . Le courant pour des potentiels répulsifs est proportionnel à l'exponentielle de la tension divisée par la température :
. Le courant pour des potentiels répulsifs est proportionnel à l'exponentielle de la tension divisée par la température : 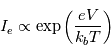

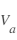 par rapport au satellite et on collecte le courant sur la sonde. Le courant
par rapport au satellite et on collecte le courant sur la sonde. Le courant 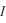 est la somme des courant ionique et électronique générés par les particules impactant la sonde. La
est la somme des courant ionique et électronique générés par les particules impactant la sonde. La 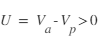 (
(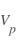 étant le potentiel du plasma) les électrons sont accélérés et les ions sont freinés. Dans le cas inverse (
étant le potentiel du plasma) les électrons sont accélérés et les ions sont freinés. Dans le cas inverse (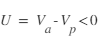 ) les électrons sont repoussés et les ions accélérés.
L'échantillonnage de la fonction de distribution des électrons en fonction du potentiel appliqué à la sonde est schématisé grâce à l'appliquette disponible à la
) les électrons sont repoussés et les ions accélérés.
L'échantillonnage de la fonction de distribution des électrons en fonction du potentiel appliqué à la sonde est schématisé grâce à l'appliquette disponible à la 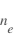 , une température
, une température 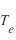 , une densité
, une densité 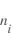 ,...
Lorsque la sonde est présente, la tension appliquée à la sonde va collecter les courants liés aux déplacement des charges électriques (ions et électrons). Du fait de la plus grande mobilité des électrons (moins massifs que les ions), les électrons vont impacter la sonde plus rapidement ce qui va créer une structure de potentiel autour de la sonde. Du coup un électron qui se trouve loin de la sonde et de sa structure de potentiel verra un potentiel différent que celui appliqué à la sonde à cause de cet écrantage. Cette région s'appelle la gaine et l'équilibre de charge entre ions et électrons est brisé.
,...
Lorsque la sonde est présente, la tension appliquée à la sonde va collecter les courants liés aux déplacement des charges électriques (ions et électrons). Du fait de la plus grande mobilité des électrons (moins massifs que les ions), les électrons vont impacter la sonde plus rapidement ce qui va créer une structure de potentiel autour de la sonde. Du coup un électron qui se trouve loin de la sonde et de sa structure de potentiel verra un potentiel différent que celui appliqué à la sonde à cause de cet écrantage. Cette région s'appelle la gaine et l'équilibre de charge entre ions et électrons est brisé.
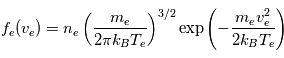
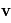 et
et 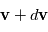 est ainsi égal à :
est ainsi égal à :
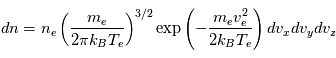
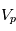 . On notera la tension
. On notera la tension 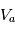 appliquée à la sonde, et
appliquée à la sonde, et 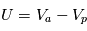 cette même tension mesurée par rapport au potentiel plasma.
cette même tension mesurée par rapport au potentiel plasma.
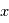 est normal au plan de la sonde. Les calculs dans le cas d'une géométrie sphérique sont proposés en exercice. On notera
est normal au plan de la sonde. Les calculs dans le cas d'une géométrie sphérique sont proposés en exercice. On notera 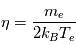
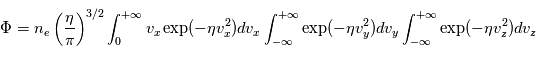
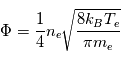
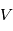 négatif (
négatif (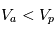 ), seuls les électrons ayant une vitesse telle que :
), seuls les électrons ayant une vitesse telle que :
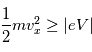 seront collectés, par contre tous les ions sont collectés.
seront collectés, par contre tous les ions sont collectés.
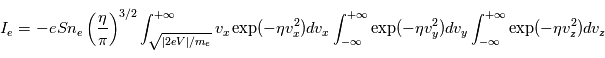 Ici,
Ici, 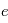 est la valeur absolue de la charge unitaire et
est la valeur absolue de la charge unitaire et 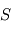 la surface de la sonde.
la surface de la sonde.
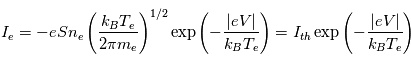 où
où 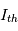 est le courant lié aux vitesses thermiques des particules. Le courant électronique est négatif à cause de la charge de l'électron.
est le courant lié aux vitesses thermiques des particules. Le courant électronique est négatif à cause de la charge de l'électron.
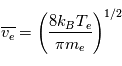 Le courant électronique s'écrit donc également :
Le courant électronique s'écrit donc également :
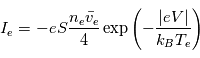
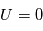 (i.e. une tension sonde égale au potentiel plasma) tous les électrons sont collectés. Pour
(i.e. une tension sonde égale au potentiel plasma) tous les électrons sont collectés. Pour 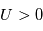 (c'est-à-dire
(c'est-à-dire 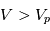 ), le courant est le même car tous les électrons sont collectés. Le courant électronique est alors constant et égal à :
), le courant est le même car tous les électrons sont collectés. Le courant électronique est alors constant et égal à :
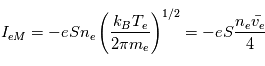 On montre alors que pour
On montre alors que pour 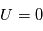 ,
, 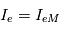 .
.
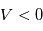 , tous les ions sont collectés et on devrait obtenir un courant ionique de saturation constant égal à :
, tous les ions sont collectés et on devrait obtenir un courant ionique de saturation constant égal à :
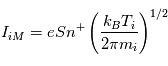
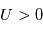 , les ions sont repoussés et seuls ceux dont la vitesse
, les ions sont repoussés et seuls ceux dont la vitesse 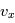 est suffisante pourront être collectés comme on l'a montré pour les électrons.
est suffisante pourront être collectés comme on l'a montré pour les électrons.
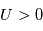 et tous les ions si
et tous les ions si 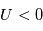 . Afin de conserver la neutralité
électrique du plasma il se crée, au voisinage de la sonde, une charge d'espace appelée ''gaine''. Les particules de même polarité que le potentiel de la surface sont exclues de cette gaine. Cette gaine est électronique si
. Afin de conserver la neutralité
électrique du plasma il se crée, au voisinage de la sonde, une charge d'espace appelée ''gaine''. Les particules de même polarité que le potentiel de la surface sont exclues de cette gaine. Cette gaine est électronique si 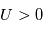 (afin de limiter le flux d'électrons) et ionique si
(afin de limiter le flux d'électrons) et ionique si 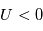 (pour limiter le flux d'ions). L'épaisseur de cette gaine est de l'ordre de grandeur de la longueur de Debye :
(pour limiter le flux d'ions). L'épaisseur de cette gaine est de l'ordre de grandeur de la longueur de Debye :
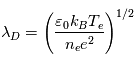
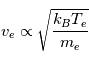 est beaucoup plus grande que la vitesse thermique des ions
est beaucoup plus grande que la vitesse thermique des ions 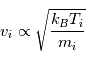 , et de ce fait plus d'électrons viennent frapper l'obstacle. Comme cet objet se charge négativement, les électrons sont repoussés. L'équilibre s'obtient lorsque le courant électronique collecté à la surface de l'objet (la sonde) vient équilibrer le courant ionique incident ce qui se produit pour une certaine valeur de potentiel que l'on appelle le potentiel flottant.
, et de ce fait plus d'électrons viennent frapper l'obstacle. Comme cet objet se charge négativement, les électrons sont repoussés. L'équilibre s'obtient lorsque le courant électronique collecté à la surface de l'objet (la sonde) vient équilibrer le courant ionique incident ce qui se produit pour une certaine valeur de potentiel que l'on appelle le potentiel flottant.
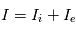 . Les paramètres plasmas
. Les paramètres plasmas 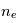 et
et 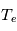 sont déterminés à partir du courant électronique
sont déterminés à partir du courant électronique 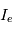 . Pour avoir accès au courant électronique, il faut éliminer la contribution du courant ionique du courant total mesuré. La
. Pour avoir accès au courant électronique, il faut éliminer la contribution du courant ionique du courant total mesuré. La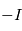 en fonction de
en fonction de 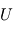 .
.
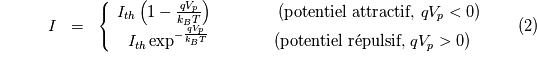
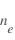 ,
, 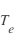 ...) à spécifier par l'utilisateur.
...) à spécifier par l'utilisateur.
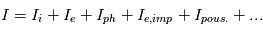

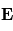 entre les deux électrodes exerce une force
entre les deux électrodes exerce une force 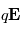 sur la particule qui va dévier la trajectoire lorsque celle-ci entre dans l'entrefer (espace entre les deux électrodes). Les particules atteignent les détecteur lorsque le rapport
sur la particule qui va dévier la trajectoire lorsque celle-ci entre dans l'entrefer (espace entre les deux électrodes). Les particules atteignent les détecteur lorsque le rapport 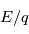 correspond à la force
correspond à la force 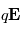 générée par le champ. En faisant varier le potentiel de l'électrode, il est possible de parcourir différentes gammes d'énergie. Les mesures présentent donc un spectre d'énergie. En analysant ce spectre, et en combinant les informations sur la couverture angulaire, il sera possible de reconstruire la fonction de distribution des électrons.
générée par le champ. En faisant varier le potentiel de l'électrode, il est possible de parcourir différentes gammes d'énergie. Les mesures présentent donc un spectre d'énergie. En analysant ce spectre, et en combinant les informations sur la couverture angulaire, il sera possible de reconstruire la fonction de distribution des électrons.
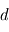 . Une des deux électrodes est reliée à la masse tandis que l'autre électrode est fixé à un potentiel
. Une des deux électrodes est reliée à la masse tandis que l'autre électrode est fixé à un potentiel 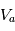 (
(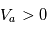 pour la détection des électrons,
pour la détection des électrons, 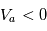 pour la détection des ions). Les particules entrent par un orifice d'entrée
positionné en
pour la détection des ions). Les particules entrent par un orifice d'entrée
positionné en 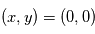 avec une vitesse
avec une vitesse 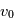 et un angle
et un angle 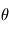 par rapport aux électrodes. Les particules voient un champ électrostatique constant qui va modifier leur trajectoire. Les particules vont ensuite impacter le détecteur situé à une distance
par rapport aux électrodes. Les particules voient un champ électrostatique constant qui va modifier leur trajectoire. Les particules vont ensuite impacter le détecteur situé à une distance 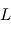 de l'orifice d'entrée. Le schéma
de l'orifice d'entrée. Le schéma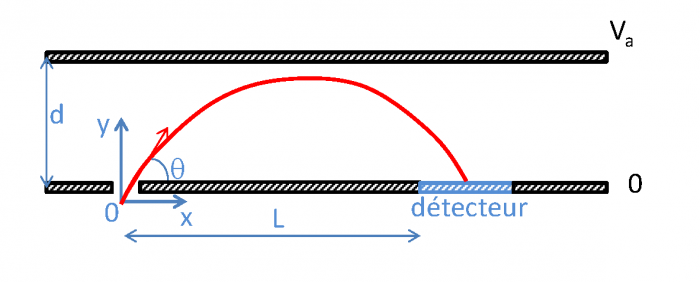
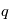 dans ce système. Nous présentons ici uniquement les résultats et les cacluls pourront être fait dans le cadre d'un exercice (cf exercice ).
Les équations paramétriques décrivant la trajectoire sont :
dans ce système. Nous présentons ici uniquement les résultats et les cacluls pourront être fait dans le cadre d'un exercice (cf exercice ).
Les équations paramétriques décrivant la trajectoire sont :
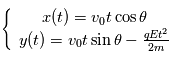
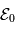 l'énergie cinétique initiale de la particule (à l'entrée du système), il est possible de relier la distance du détecteur (
l'énergie cinétique initiale de la particule (à l'entrée du système), il est possible de relier la distance du détecteur (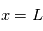 ) à l'énergie.
) à l'énergie.
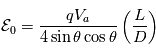
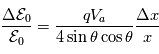

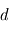 de l'entrefer, des particules avec une composante non nulle suivant le plan d'entrée de l'analyseur peuvent également se propager jusqu'à la sortie. Cela a pour conséquence d'augmenter la gamme d'énergie car les particules entrant dans l'analyseur avec un angle important par rapport à la normale peuvent être sélectionnées quand bien même leur énergie totale peut se trouver en dehors de la gamme d'énergie filtrée.
de l'entrefer, des particules avec une composante non nulle suivant le plan d'entrée de l'analyseur peuvent également se propager jusqu'à la sortie. Cela a pour conséquence d'augmenter la gamme d'énergie car les particules entrant dans l'analyseur avec un angle important par rapport à la normale peuvent être sélectionnées quand bien même leur énergie totale peut se trouver en dehors de la gamme d'énergie filtrée.
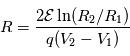 où
où 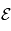 est l'énergie cinétique de la particule,
est l'énergie cinétique de la particule, 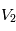 et
et 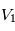 sont les potentiels appliqués aux deux électrodes.
sont les potentiels appliqués aux deux électrodes.
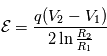
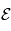 (en eV) de la particule qui passe dans l'analyseur et la tension
(en eV) de la particule qui passe dans l'analyseur et la tension 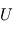 appliquée entre les deux électrodes séparées de la fente de sortie d'une distance
appliquée entre les deux électrodes séparées de la fente de sortie d'une distance 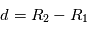 . La bande d'énergie
. La bande d'énergie 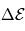 des particules qui passent à travers l'analyseur vaut :
des particules qui passent à travers l'analyseur vaut :
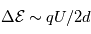 Une extension naturelle des analyseurs à secteur cyindrique à deux dimensions est de former des analyseurs à secteurs sphériques et les analyseurs électrostatiques hémisphériques ''top-hat''.
Une extension naturelle des analyseurs à secteur cyindrique à deux dimensions est de former des analyseurs à secteurs sphériques et les analyseurs électrostatiques hémisphériques ''top-hat''.
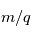 ) pour séparer les atomes et molécules ionisés. La spectrométrie de masse est l'une des techniques analytiques les plus sensibles et est fréquemment utilisée pour déterminer les propriétés du plasma. Le spectre de masse contient des informations sur la composition élémentaire (présence et nombre de certains éléments), l'abondance isotopique (la masse exacte) et la structure (les fragments).
) pour séparer les atomes et molécules ionisés. La spectrométrie de masse est l'une des techniques analytiques les plus sensibles et est fréquemment utilisée pour déterminer les propriétés du plasma. Le spectre de masse contient des informations sur la composition élémentaire (présence et nombre de certains éléments), l'abondance isotopique (la masse exacte) et la structure (les fragments).
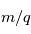 ). Dans le domaine spatial, le plasma est le milieu d'étude et la source d'ionisation n'est généralement pas nécessaire (sauf si on souhaite caractériser les atmosphères neutres planétaires). L'instrument se réduit donc à la partie analyseur.
). Dans le domaine spatial, le plasma est le milieu d'étude et la source d'ionisation n'est généralement pas nécessaire (sauf si on souhaite caractériser les atmosphères neutres planétaires). L'instrument se réduit donc à la partie analyseur.
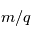 basés sur la déviation des trajectoires de particules ionisés dans un secteur magnétique. Dans le secteur magnétique, la trajectoire des ions est plane et est située dans le plan perpendiculaire à
basés sur la déviation des trajectoires de particules ionisés dans un secteur magnétique. Dans le secteur magnétique, la trajectoire des ions est plane et est située dans le plan perpendiculaire à 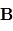 . La trajectoire est circulaire avec un rayon
. La trajectoire est circulaire avec un rayon 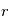 .
.

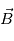 . Le mouvement d'une particule non-relativiste dans un tel champ est donné par :
. Le mouvement d'une particule non-relativiste dans un tel champ est donné par :
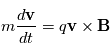
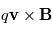 est la force de Lorentz. En prenant le produit scalaire de l'équation ci-dessus avec le vecteur vitesse, nous obtenons
est la force de Lorentz. En prenant le produit scalaire de l'équation ci-dessus avec le vecteur vitesse, nous obtenons
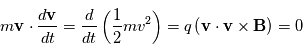
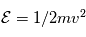 est une constante du mouvement. Pour déterminer la trajectoire il est avantageux de séparer les composantes des vitesses parallèle et perpendiculaire au champ magnétique. Soit
est une constante du mouvement. Pour déterminer la trajectoire il est avantageux de séparer les composantes des vitesses parallèle et perpendiculaire au champ magnétique. Soit 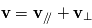
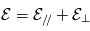 où
où 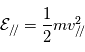 et
et 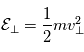 .
Comme la force
.
Comme la force 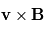 n'a pas de composante parallèle au champ magnétique, la composante parallèle de la vitesse est constante, donc la particule se déplace avec un vitesse constante le long du champ
n'a pas de composante parallèle au champ magnétique, la composante parallèle de la vitesse est constante, donc la particule se déplace avec un vitesse constante le long du champ 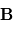 (sauf si
(sauf si 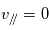 ). Puisque
). Puisque 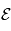 et
et 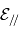 sont constants alors
sont constants alors 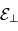 (et de ce fait
(et de ce fait 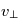 ) sont également des constantes du mouvement.
) sont également des constantes du mouvement.
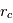 du mouvement de la particule dans le plan perpendiculaire à
du mouvement de la particule dans le plan perpendiculaire à 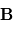 peut s'écrire (en ignorant le signe) :
peut s'écrire (en ignorant le signe) :
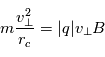 Le rayon
Le rayon 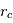 est souvent appelé le rayon de Larmor
est souvent appelé le rayon de Larmor
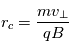
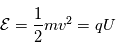 (
(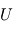 est la tension d'accélération utilisé dans l'analyseur électrostatique). La vitesse des ions vaut donc
est la tension d'accélération utilisé dans l'analyseur électrostatique). La vitesse des ions vaut donc 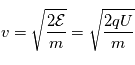 On obtient ainsi la mesure de masse sur charge :
On obtient ainsi la mesure de masse sur charge :
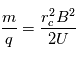
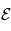 , on mesure le temps que la particule met pour effectuer la distance entre la source et le détecteur. Connaissant le temps de parcours et la distance parcourue, on en déduit la vitesse. Comme l'énergie de la particule est déterminé on peut en déduire sa masse.
, on mesure le temps que la particule met pour effectuer la distance entre la source et le détecteur. Connaissant le temps de parcours et la distance parcourue, on en déduit la vitesse. Comme l'énergie de la particule est déterminé on peut en déduire sa masse.
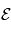 deux particules de masse
deux particules de masse 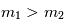 auront des vitesses telles que
auront des vitesses telles que 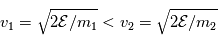 . C'est-à-dire que la vitesse de la particule légère (
. C'est-à-dire que la vitesse de la particule légère (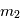 ) sera plus grande que la vitesse de la particule lourde (
) sera plus grande que la vitesse de la particule lourde (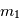 ). Comme les deux particules ont parcouru la même distance
). Comme les deux particules ont parcouru la même distance 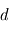 on trouve que le temps de parcours de la particule légère
on trouve que le temps de parcours de la particule légère 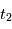 sera plus bref que celui de la particule lourde
sera plus bref que celui de la particule lourde 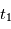 .
.
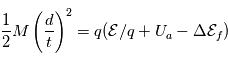 avec
avec 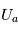 un potentiel de post-accélération et
un potentiel de post-accélération et 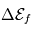 l'énergie perdue lors de collision à travers une feuille de carbone (cf ci-dessous).
Soit
l'énergie perdue lors de collision à travers une feuille de carbone (cf ci-dessous).
Soit
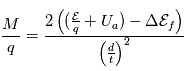

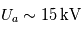 ).
).
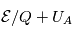 , où
, où 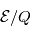 est l'énergie des particules en sortie de l'analyseur électrostatique.
est l'énergie des particules en sortie de l'analyseur électrostatique.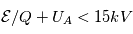 , ils viendront impacter le détecteur LEF et produiront un signal STOP. La différence de temps entre le signal de départ et le signal d'arrivée permettra d'en déduire le temps de vol. Dans ce cas de figure le champ électrostatique agit sur la trajectoire de la particule (
, ils viendront impacter le détecteur LEF et produiront un signal STOP. La différence de temps entre le signal de départ et le signal d'arrivée permettra d'en déduire le temps de vol. Dans ce cas de figure le champ électrostatique agit sur la trajectoire de la particule (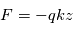 ) et l'équation de mouvement suivant la direction
) et l'équation de mouvement suivant la direction 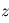 est celle d'un oscillateur harmonique. On en déduit le temps de vol tel que
est celle d'un oscillateur harmonique. On en déduit le temps de vol tel que 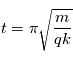 .
.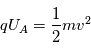 Dans la région de champ libre, l'énergie de la particule n'évolue pas. Le temps
Dans la région de champ libre, l'énergie de la particule n'évolue pas. Le temps  pour parcourir la distance
pour parcourir la distance 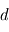 est lié à sa vitesse
est lié à sa vitesse 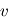 .
.
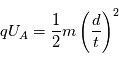 On en déduit le temps de vol
On en déduit le temps de vol
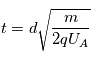

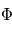 à travers
à travers 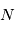 spires induit une tension électrique
spires induit une tension électrique 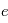 :
:
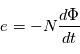 On rappelle que le flux du champ d'induction magnétique
On rappelle que le flux du champ d'induction magnétique 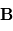 traversant une surface fermée
traversant une surface fermée 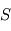 est
est 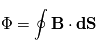 , où
, où 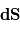 est un vecteur élémentaire de surface.
est un vecteur élémentaire de surface.

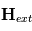 . Le bobinage d'excitation a pour effet de saturer le matériau magnétique périodiquement à la fréquence fondamentale
. Le bobinage d'excitation a pour effet de saturer le matériau magnétique périodiquement à la fréquence fondamentale 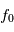 (une dizaine de kHz). Le bobinage d'excitation crée un champ alternatif dans le matériau ferromagnétique. L'induction générée est limitée par la saturation du matériau. Le second bobinage est utilisé comme élément de détection et est appelé sense winding ou bobinage de mesure. À ces bornes, une tension est induite par la variation temporelle du flux magnétique total.
(une dizaine de kHz). Le bobinage d'excitation crée un champ alternatif dans le matériau ferromagnétique. L'induction générée est limitée par la saturation du matériau. Le second bobinage est utilisé comme élément de détection et est appelé sense winding ou bobinage de mesure. À ces bornes, une tension est induite par la variation temporelle du flux magnétique total.
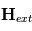 se trouve dans le plan du tore, on va pouvoir déterminer sa direction. Lorsque le courant traverse le bobinage d'excitation, la moitié va générer un champ avec une composante dans la même direction que
se trouve dans le plan du tore, on va pouvoir déterminer sa direction. Lorsque le courant traverse le bobinage d'excitation, la moitié va générer un champ avec une composante dans la même direction que 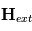 et l'autre moitié dans la direction opposée.
et l'autre moitié dans la direction opposée.
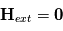 ), les deux demi-tores entrent dans la région de saturation (cf
), les deux demi-tores entrent dans la région de saturation (cf 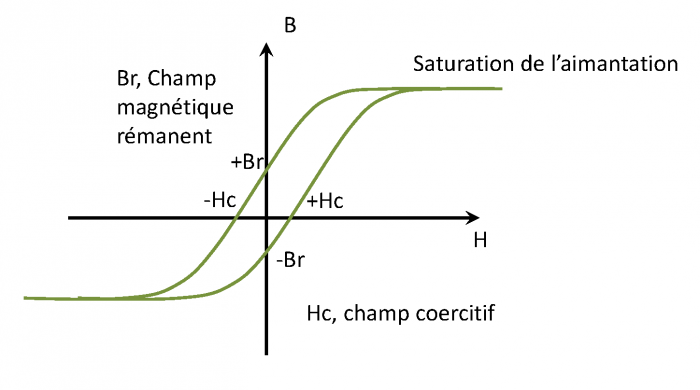
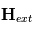 provoque l'apparation d'harmoniques pairs dans la tension induite en raison du comportement non-linéaire du matériau magnétique. On extrait l'amplitude et la phase pour déterminer l'amplitude et la direction du champ. On utilise la mesure du champ magnétique d'induction qui est contenue dans les harmoniques du signal. Le second harmonique
provoque l'apparation d'harmoniques pairs dans la tension induite en raison du comportement non-linéaire du matériau magnétique. On extrait l'amplitude et la phase pour déterminer l'amplitude et la direction du champ. On utilise la mesure du champ magnétique d'induction qui est contenue dans les harmoniques du signal. Le second harmonique 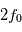 est généralement utilisé.
est généralement utilisé.
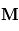 est liée au champ magnétique d'excitation
est liée au champ magnétique d'excitation 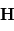 par la relation
par la relation 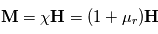 où
où 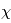 et
et 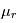 sont respectivement la susceptibilité et perméabilité magnétique (
sont respectivement la susceptibilité et perméabilité magnétique (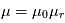 ).
).
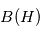 présentée à la
présentée à la 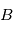 est le champ d'induction magnétique (en T) et
est le champ d'induction magnétique (en T) et 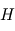 est le champ magnétique (en
est le champ magnétique (en 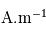 ).
).
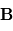 , le champ magnétique
, le champ magnétique 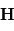 et l'aimantation
et l'aimantation 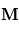 sont reliés par la relation :
sont reliés par la relation :
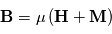
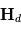 a la même direction que le champ qui lui a donné naissance mais est de sens opposé :
a la même direction que le champ qui lui a donné naissance mais est de sens opposé : 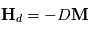 où
où 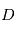 est le coefficient démagnétisant.
est le coefficient démagnétisant.
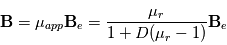 où
où 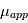 est la perméabilité apparente (tenant en compte l'effet démagnétisant). On rappelle que la perméablité magnétique du matériau est une fonction du champ magnétique :
est la perméabilité apparente (tenant en compte l'effet démagnétisant). On rappelle que la perméablité magnétique du matériau est une fonction du champ magnétique : ![\mu_r = \mu_r\left[H(t)\right]](../pages_mesures-insitu/equations_magnetometre/equation35.png) .
.
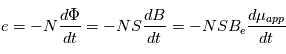 (si
(si 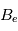 est constant). Soit, en utilisant l'expression de
est constant). Soit, en utilisant l'expression de 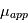 déterminée précédemment :
déterminée précédemment : 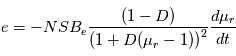 Il s'agit de l'équation basique des magnétomètres à vanne de flux.
Il s'agit de l'équation basique des magnétomètres à vanne de flux.
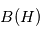 présentée à la
présentée à la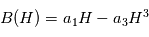
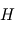 comprend à la fois le champ externe à mesurer
comprend à la fois le champ externe à mesurer 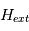 et le champ ''interne''
et le champ ''interne'' 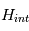 induit par le courant imposé dans le bobinage d'excitation (
induit par le courant imposé dans le bobinage d'excitation (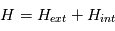 ).
).
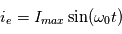 , on induit un champ magnétique de la forme sinusoïdale
, on induit un champ magnétique de la forme sinusoïdale 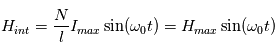
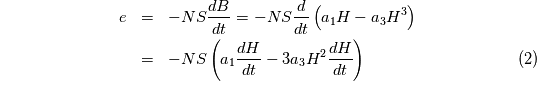
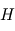 par son expression
par son expression 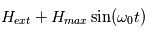 , et en développant puis en linéarisant les fonctions trigonomériques, on montre (après quelques lignes de calculs laissées à la discrétion du lecteur) que la tension induite peut s'écrire :
, et en développant puis en linéarisant les fonctions trigonomériques, on montre (après quelques lignes de calculs laissées à la discrétion du lecteur) que la tension induite peut s'écrire :
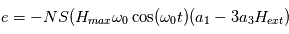
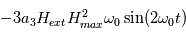
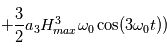
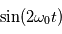 qui dépend de
qui dépend de 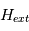 , la deuxième harmonique (de fréquence
, la deuxième harmonique (de fréquence 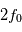 ). On cherchera donc à extraire cette information. D'autres harmoniques peuvent être présentes (dans cette démonstration nous avons modélisé la courbe
). On cherchera donc à extraire cette information. D'autres harmoniques peuvent être présentes (dans cette démonstration nous avons modélisé la courbe 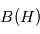 par un polynôme de troisième degré, si l'on considère un polynôme de degré plus élevé d'autres harmoniques apparaîtront dans les calculs).
par un polynôme de troisième degré, si l'on considère un polynôme de degré plus élevé d'autres harmoniques apparaîtront dans les calculs).
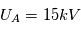 . La particule impacte le détecteur après un temps de vol de
. La particule impacte le détecteur après un temps de vol de 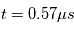 .
.
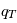 située en un point O placée dans un plasma dont le densité particulaire, à la distance r de O, peut s'écrire
pour les ions :
située en un point O placée dans un plasma dont le densité particulaire, à la distance r de O, peut s'écrire
pour les ions :
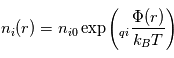
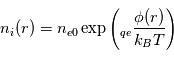
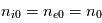 (hypothèse de quasi-neutralité du plasma) est la densité particulaire moyenne,
(hypothèse de quasi-neutralité du plasma) est la densité particulaire moyenne, 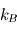 est la constante de Boltzmann,
est la constante de Boltzmann, 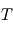 est la température,
est la température, 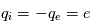 est la chage des particules, et
est la chage des particules, et 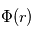 est le potentiel qui règne à la distance
est le potentiel qui règne à la distance 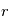 de O.
de O.
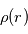
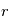 et
et 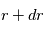 , donner l'équation satisfaite par le champ électrostatique. En déduire une équation différentielle de deuxième ordre sur le potentiel
, donner l'équation satisfaite par le champ électrostatique. En déduire une équation différentielle de deuxième ordre sur le potentiel 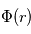
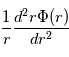
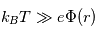 . Simplifier l'équation précédente et la résoudre.
La solution approche le potentiel de Coulomb de
. Simplifier l'équation précédente et la résoudre.
La solution approche le potentiel de Coulomb de 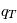 quand
quand 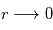 et reste finie à toutes les distances.
et reste finie à toutes les distances.
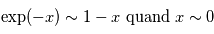
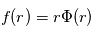 pour résoudre plus facilement l'équation différentielle
pour résoudre plus facilement l'équation différentielle
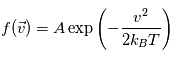
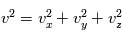 ,
, 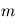 la masse des particules,
la masse des particules, 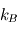 la constante de Boltzamnn,
la constante de Boltzamnn, 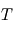 la température et
la température et 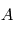 une quantité réelle.
une quantité réelle.
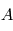 telle que
telle que
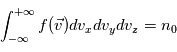
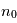 est la densité des particules
est la densité des particules
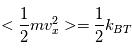
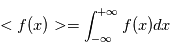
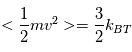
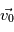
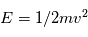 et effectuer le changement de variable
et effectuer le changement de variable 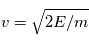
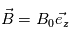 . On cherche à déterminer le mouvement de la particule dans ce champ magnétique. On se place dans un repère cartésien orthonormé
. On cherche à déterminer le mouvement de la particule dans ce champ magnétique. On se place dans un repère cartésien orthonormé 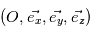 . A t=0 la position de la particule est telle que
. A t=0 la position de la particule est telle que 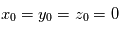 et sa vitesse intiale est définie par
et sa vitesse intiale est définie par 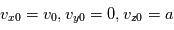 .
.
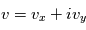
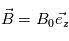 mais qu'un champ électrique est désormais présent tel que
mais qu'un champ électrique est désormais présent tel que 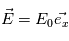 . Comment la trajectoire est-elle modifiée ?
. Comment la trajectoire est-elle modifiée ?
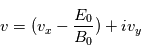
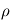 à l'axe du tore.
à l'axe du tore.
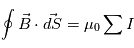
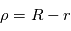 et
et 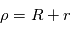
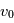 , et avec un angle
, et avec un angle 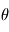 entre le vecteur vitesse de la particule et l'axe x du montage. On cherche à caractériser le mouvement de cetteparticule chargée.
entre le vecteur vitesse de la particule et l'axe x du montage. On cherche à caractériser le mouvement de cetteparticule chargée.
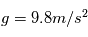 ,
, 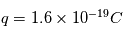 ,
, 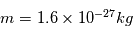 ,
, 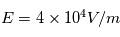
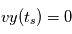

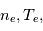 ...). L'ajustement peu se faire par exemple par une méthode de moindre carrés. On en déduira les valeurs de
...). L'ajustement peu se faire par exemple par une méthode de moindre carrés. On en déduira les valeurs de 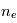 et
et 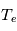 à trouver et on comparera notre résultat à celui produit par les équipes de Cassini (valeurs vers 11h40 de la
à trouver et on comparera notre résultat à celui produit par les équipes de Cassini (valeurs vers 11h40 de la 
