Trajectoire des particules dans l'analyseur

Auteur: Ronan Modolo

Energie des particules et position du détecteur

Il est possible de décrire analytiquement la trajectoire d'une particule de charge 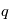dans ce système. Nous présentons ici uniquement les résultats et les cacluls pourront être fait dans le cadre d'un exercice (cf exercice ). Les équations paramétriques décrivant la trajectoire sont :

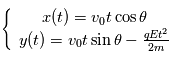
$\left\{\begin{array}{c}x(t) = v_0t\cos\theta \\y(t) = v_0t\sin\theta-\frac{qEt^2}{2m}\end{array}\right.$

En notant 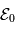$\mathcal{E}_0$ l'énergie cinétique initiale de la particule (à l'entrée du système), il est possible de relier la distance du détecteur ( 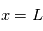x=L ) à l'énergie.

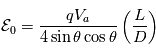
$\mathcal{E}_0 = \frac{qV_a}{4\sin\theta\cos\theta}\left(\frac{L}{D}\right)$

A partir d'un simple calcul d'incertitude il est possible de montrer que la résolution relative en énergie dépend de la position du détecteur et de sa largeur.

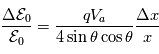
$\frac{\Delta\mathcal{E}_0}{\mathcal{E}_0} = \frac{qV_a}{4\sin\theta\cos\theta}\frac{\Delta x}{x}$

Ainsi en balayant le potentiel appliqué à l'électrode on pourra couvrir différentes gammes d'énergie et reconstruire la fonction de distribution en énergie.