 Principe de fonctionement
Principe de fonctionement
Pour illustration nous prenons comme exemple le spectromètre électronique embarqué sur la mission Spatiale Cassini. Plus d'informations sont disponibles dans le papier de description instrumentale Young et al, Space Science Reviews, ..., 2004.
Ce spectromètre a été construit par le Mullard Space Science Laboratory, Angleterre.
Un schéma simplifié de l'instrument est présenté à la figure suivante. Cet instrument est essentiellement un analyseur électrostatique hémisphérique de type 'top-hat' (en référence au fait qu'une petite section d'analyseur se trouve placée au dessus des électrodes de déflection).
Schéma d'un spectromètre électronique
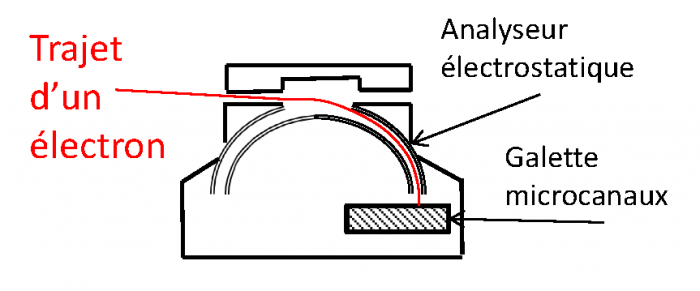
Représentation schématique du spectromètre électronique embarqué sur la mission Cassini et la trajectoire possible d'un électron en rouge.
Crédit :
Ce schéma est une version adaptée de la figure 3 de Young et al, SSR, 2004
Les électrons entrent dans le senseur via une des huit fenêtres d'entrées qui consiste en un baffle collimateur (les huit fenêtres définissent le champ de vue de l'instrument, c'est-à-dire sa couverture angulaire ). Ces électrons sont ensuite dirigés dans l'analyseur électrostatique jusqu'au détecteur, qui dans le cas du spectromètre électronique de Cassini sont des galettes micro-canaux. Ces galettes permettent la détection des particules chargées. La sélection en énergie s'effectue dans l'analyseur électrostatique. L'analyseur consiste en deux plaques/électrodes ayant pour l'une un potentiel nul et pour l'autre un potentiel que l'on applique. Le champ électrique 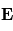 entre les deux électrodes exerce une force
entre les deux électrodes exerce une force 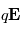 sur la particule qui va dévier la trajectoire lorsque celle-ci entre dans l'entrefer (espace entre les deux électrodes). Les particules atteignent les détecteur lorsque le rapport
sur la particule qui va dévier la trajectoire lorsque celle-ci entre dans l'entrefer (espace entre les deux électrodes). Les particules atteignent les détecteur lorsque le rapport 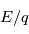 correspond à la force
correspond à la force 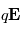 générée par le champ. En faisant varier le potentiel de l'électrode, il est possible de parcourir différentes gammes d'énergie. Les mesures présentent donc un spectre d'énergie. En analysant ce spectre, et en combinant les informations sur la couverture angulaire, il sera possible de reconstruire la fonction de distribution des électrons.
générée par le champ. En faisant varier le potentiel de l'électrode, il est possible de parcourir différentes gammes d'énergie. Les mesures présentent donc un spectre d'énergie. En analysant ce spectre, et en combinant les informations sur la couverture angulaire, il sera possible de reconstruire la fonction de distribution des électrons.
L'appliquette \ref{appliquette_analyseur_electrostatique} présente brièvement le mode de fonctionnement d'un analyseur électrostatique et la trajectoire d'un électron pour une énergie incidente fixée par l'utilisateur. Les potentiels des deux électrodes ont été fixés (valeurs non connues de l'utilisateur) et il s'agit de déterminer la bande passante en énergie.
Nous présentons deux cas simples d'analyseur électrostatique :
Les analyseurs sphériques ou hémisphériques sont des extensions naturelles de ces deux types d'analyseurs et ne présentent pas de concepts différents, seuls les calculs sont un peu plus compliqués.
Pour illustrer la théorie qui se cache derrière le fonctionnement d'un analyseur électrostatique nous prendrons le cas d'un analsyeur à électrodes parallèles (cf Figure). Notons que ce genre d'instrument n'a pas été embarqué à bord de missions spatiales et est utilisé juste dans le cadre d'explication du concept sur une géométrie simple.
Energie des particules et position du détecteur
Il est possible de décrire analytiquement la trajectoire d'une particule de charge 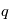 dans ce système. Nous présentons ici uniquement les résultats et les cacluls pourront être fait dans le cadre d'un exercice (cf exercice ).
Les équations paramétriques décrivant la trajectoire sont :
dans ce système. Nous présentons ici uniquement les résultats et les cacluls pourront être fait dans le cadre d'un exercice (cf exercice ).
Les équations paramétriques décrivant la trajectoire sont :
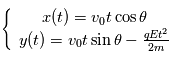
En notant 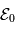 l'énergie cinétique initiale de la particule (à l'entrée du système), il est possible de relier la distance du détecteur (
l'énergie cinétique initiale de la particule (à l'entrée du système), il est possible de relier la distance du détecteur (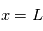 ) à l'énergie.
) à l'énergie.
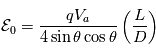
A partir d'un simple calcul d'incertitude il est possible de montrer que la résolution relative en énergie dépend de la position du détecteur et de sa largeur.
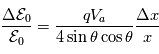
Ainsi en balayant le potentiel appliqué à l'électrode on pourra couvrir différentes gammes d'énergie et reconstruire la fonction de distribution en énergie.
 Configuration
Configuration
Un autre analyseur électrostatique simple a une géométrie cylindrique. Cet analyseur est constitué de deux secteurs cylindriques concentriques (cf Figure). Ce type d'analyseur a été utilisé lors de la mission spatiale Mariner 2. Cet analyseur a entre autre permis de fournir la confirmation expérimentale d'un vent solaire continu et de déterminer ses propriétés élémentaires [Snyder and Neugebauer, 1962].
Représentation schématique d'un analyseur à secteur cylindrique
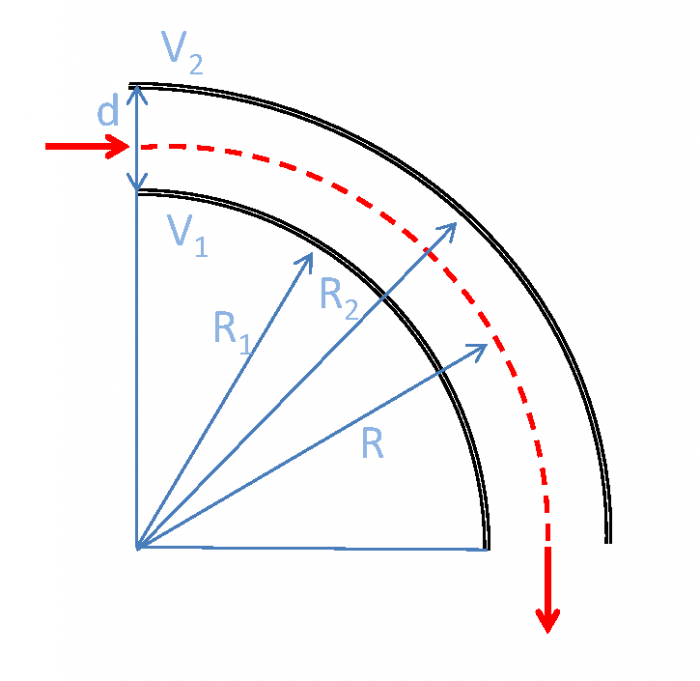
À cause de la géométrie cylindrique, seules les particules avec une vitesse parallèle à la normale du plan d'entrée de l'analyseur peuvent entrer dans celui-ci. Or avec une largeur 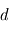 de l'entrefer, des particules avec une composante non nulle suivant le plan d'entrée de l'analyseur peuvent également se propager jusqu'à la sortie. Cela a pour conséquence d'augmenter la gamme d'énergie car les particules entrant dans l'analyseur avec un angle important par rapport à la normale peuvent être sélectionnées quand bien même leur énergie totale peut se trouver en dehors de la gamme d'énergie filtrée.
de l'entrefer, des particules avec une composante non nulle suivant le plan d'entrée de l'analyseur peuvent également se propager jusqu'à la sortie. Cela a pour conséquence d'augmenter la gamme d'énergie car les particules entrant dans l'analyseur avec un angle important par rapport à la normale peuvent être sélectionnées quand bien même leur énergie totale peut se trouver en dehors de la gamme d'énergie filtrée.
 Principe de fonctionement
Principe de fonctionement
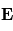 entre les deux électrodes exerce une force
entre les deux électrodes exerce une force 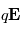 sur la particule qui va dévier la trajectoire lorsque celle-ci entre dans l'entrefer (espace entre les deux électrodes). Les particules atteignent les détecteur lorsque le rapport
sur la particule qui va dévier la trajectoire lorsque celle-ci entre dans l'entrefer (espace entre les deux électrodes). Les particules atteignent les détecteur lorsque le rapport 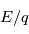 correspond à la force
correspond à la force 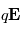 générée par le champ. En faisant varier le potentiel de l'électrode, il est possible de parcourir différentes gammes d'énergie. Les mesures présentent donc un spectre d'énergie. En analysant ce spectre, et en combinant les informations sur la couverture angulaire, il sera possible de reconstruire la fonction de distribution des électrons.
générée par le champ. En faisant varier le potentiel de l'électrode, il est possible de parcourir différentes gammes d'énergie. Les mesures présentent donc un spectre d'énergie. En analysant ce spectre, et en combinant les informations sur la couverture angulaire, il sera possible de reconstruire la fonction de distribution des électrons.
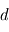 . Une des deux électrodes est reliée à la masse tandis que l'autre électrode est fixé à un potentiel
. Une des deux électrodes est reliée à la masse tandis que l'autre électrode est fixé à un potentiel 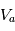 (
(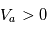 pour la détection des électrons,
pour la détection des électrons, 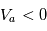 pour la détection des ions). Les particules entrent par un orifice d'entrée
positionné en
pour la détection des ions). Les particules entrent par un orifice d'entrée
positionné en 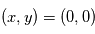 avec une vitesse
avec une vitesse 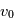 et un angle
et un angle 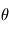 par rapport aux électrodes. Les particules voient un champ électrostatique constant qui va modifier leur trajectoire. Les particules vont ensuite impacter le détecteur situé à une distance
par rapport aux électrodes. Les particules voient un champ électrostatique constant qui va modifier leur trajectoire. Les particules vont ensuite impacter le détecteur situé à une distance 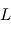 de l'orifice d'entrée. Le schéma
de l'orifice d'entrée. Le schéma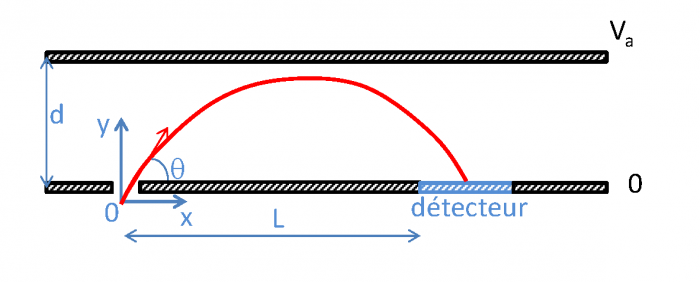
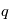 dans ce système. Nous présentons ici uniquement les résultats et les cacluls pourront être fait dans le cadre d'un exercice (cf exercice ).
Les équations paramétriques décrivant la trajectoire sont :
dans ce système. Nous présentons ici uniquement les résultats et les cacluls pourront être fait dans le cadre d'un exercice (cf exercice ).
Les équations paramétriques décrivant la trajectoire sont :
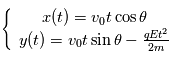
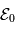 l'énergie cinétique initiale de la particule (à l'entrée du système), il est possible de relier la distance du détecteur (
l'énergie cinétique initiale de la particule (à l'entrée du système), il est possible de relier la distance du détecteur (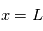 ) à l'énergie.
) à l'énergie.
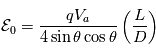
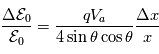

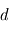 de l'entrefer, des particules avec une composante non nulle suivant le plan d'entrée de l'analyseur peuvent également se propager jusqu'à la sortie. Cela a pour conséquence d'augmenter la gamme d'énergie car les particules entrant dans l'analyseur avec un angle important par rapport à la normale peuvent être sélectionnées quand bien même leur énergie totale peut se trouver en dehors de la gamme d'énergie filtrée.
de l'entrefer, des particules avec une composante non nulle suivant le plan d'entrée de l'analyseur peuvent également se propager jusqu'à la sortie. Cela a pour conséquence d'augmenter la gamme d'énergie car les particules entrant dans l'analyseur avec un angle important par rapport à la normale peuvent être sélectionnées quand bien même leur énergie totale peut se trouver en dehors de la gamme d'énergie filtrée.
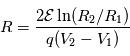 où
où 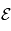 est l'énergie cinétique de la particule,
est l'énergie cinétique de la particule, 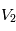 et
et 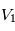 sont les potentiels appliqués aux deux électrodes.
sont les potentiels appliqués aux deux électrodes.
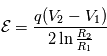
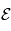 (en eV) de la particule qui passe dans l'analyseur et la tension
(en eV) de la particule qui passe dans l'analyseur et la tension 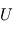 appliquée entre les deux électrodes séparées de la fente de sortie d'une distance
appliquée entre les deux électrodes séparées de la fente de sortie d'une distance 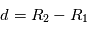 . La bande d'énergie
. La bande d'énergie 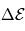 des particules qui passent à travers l'analyseur vaut :
des particules qui passent à travers l'analyseur vaut :
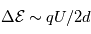 Une extension naturelle des analyseurs à secteur cyindrique à deux dimensions est de former des analyseurs à secteurs sphériques et les analyseurs électrostatiques hémisphériques ''top-hat''.
Une extension naturelle des analyseurs à secteur cyindrique à deux dimensions est de former des analyseurs à secteurs sphériques et les analyseurs électrostatiques hémisphériques ''top-hat''.