Les orbites planétaires
Auteur: Valérie Ciarletti, Lucie Maquet
- Décrire
- Un très bref historique sur l'étude et la modélisation des orbites
- Les lois de Kepler
- La première loi de Kepler (1605)
- La deuxième loi de Kepler (1604)
- La troisième loi de Kepler (1618)
- Mouvement de deux corps sous l'effet de la gravitation
- La Migration des planètes
- Comprendre
- Mouvement d'une planète autour de son étoile - Introduction
- Le problème à deux corps
- Equation du mouvement lorsque l'étoile est beaucoup plus massive que la planète
- Etude du mouvement
- Etude du mouvement
- Equation de la trajectoire
- Exercice sur la trajectoire circulaire
- Forme des trajectoires
- description des orbites
- Méthodes de détection des exoplanètes fondées sur le mouvement
- Problème à N corps
- Les points de Lagrange
- Se tester
- Mini Projet
-
Les orbites planétaires
Plusieurs milliers d’exoplanètes, en orbite autour d'étoiles autres que le Soleil, ont été détectées à ce jour. La plupart d'entre elles ont été découvertes en étudiant les variations de luminosité liées à leur passage devant leur étoile (méthode des transits) et grâce à l'observation du mouvement de l'étoile autour de laquelle les planètes sont en orbite (méthode des vitesses radiales). Ces deux méthodes reposent sur l'exploitation d'informations liées à l'interaction gravitationnelle entre la planète et son étoile.
Ce cours est essentiellement un cours de mécanique. Il a pour objectif de modéliser le mouvement d'une planète autour de son étoile et d'en identifier les paramètres caractéristiques.
La partie Décrire présente les phénomènes de façon aussi simple que possible et ne requiert pas de compétences en mathématique.
La partie Comprendre s'attache à démontrer les résultats énoncés dans la partie précédente.
Le problème à deux corps (interaction entre une planète et son étoile) est au coeur de ce module. Le problème à plus de deux corps, qui est mathématiquement nettement plus compliqué, sera uniquement évoqué et permettra d'introduire les points dits de Lagrange. La migration des planètes sera également évoquée.
Les illustrations seront systématiquement empruntées au monde des exoplanètes.
Décrire
Auteur: Valérie Ciarletti et Lucie Maquet
Un très bref historique sur l'étude et la modélisation des orbites
Les exoplanètes, comme les planètes et autres corps de notre système solaire sont soumises à la loi de la gravitation ou attraction universelle. Cette loi a été historiquement formalisée par Isaac Newton en 1687. Elle permet de modéliser, de façon générale, l'attraction entre des corps ayant une masse et, par conséquent, le mouvement des corps célestes.
Copernic
Modèle héliocentrique de Copernic , Caelestial Orbes, 1576
Bien avant Newton, le mouvement des planètes dans le ciel a retenu l'attention de nombreux scientifiques (Aristote, Galilée, Copernic,...) qui ont proposé des modèles pour expliquer ou, au moins, modéliser leurs observations.
Les travaux de Copernic font date avec sa proposition en 1543 d'un modèle héliocentrique qui présente, entre autres, le grand avantage de simplifier les calculs par rapport au modèle géocentrique. Cependant, la cause du mouvement n'est pas identifiée et les orbites des planètes restent des cercles.
Johannes Kepler établit, à partir des observations minutieuses du mouvement de Vénus, Mars, Jupiter et Saturne faites par Tycho Brahe, le fait que les orbites des planètes de notre système solaire ne sont pas des cercles mais des ellipses dont le Soleil est un foyer. Il publie, en 1609 et 1619, des lois empiriques qui prendront le nom de Lois de Kepler. Ces lois sont particulièrement intéressantes et utiles parce qu'elles établissent des relations entre les différents paramètres des orbites. En outre, il faut noter que Kepler a certainement ouvert la voie à Newton en affirmant que "deux corps voisins et hors de la sphère d'attraction d'un troisième corps s'attireraient en raison directe de leur masse."
Newton a finalement modélisé la gravitation est ainsi permis une explication des phénomènes observés ainsi que la possibilité de prédire le mouvement des planètes en orbite autour de leur soleil. Les lois de la gravitation de Newton permettront d'ailleurs d'expliquer les résultats empiriques énoncés dans les lois de Kepler.
Notons que la mécanique classique issue des lois de Newton n'est elle-même qu'une approximation, qui ne rend plus bien compte des mouvements des corps aux vitesses très élevées ou au voisinage immédiat des masses. Ainsi c'est la relativité générale d'Einstein qui a permis d'expliquer le mouvement du périhélie de Mercure ce qui n'était pas possible à partir des lois de Newton.
Les lois de Kepler
Kepler

Portait de Johannes Kepler (1571-1630) réalisé en 1610 - Artiste inconnu
Brahe

Portait de Tycho Brahe (1546-1601) réalisé en 1596 - Artiste inconnu
Les trois lois de Kepler ont été établies à partir de l'observation du mouvement des planètes au sein de notre système solaire. Elles ne reposent sur aucune modélisation mécanique de l'interaction entre la planète et le soleil.
Néanmoins, ces lois seront confirmées, a posteriori, par la théorie de la gravitation universelle.
Dans cette partie, ces lois sont énoncées sans démonstration (les démonstrations seront faites plus loin) et illustrées.
La première loi de Kepler (1605)
Loi des orbites : Les planètes autour de leur soleil ont un mouvement périodique dans un plan. Plus précisément, ces orbites sont des ellipses dont le soleil est un foyer.
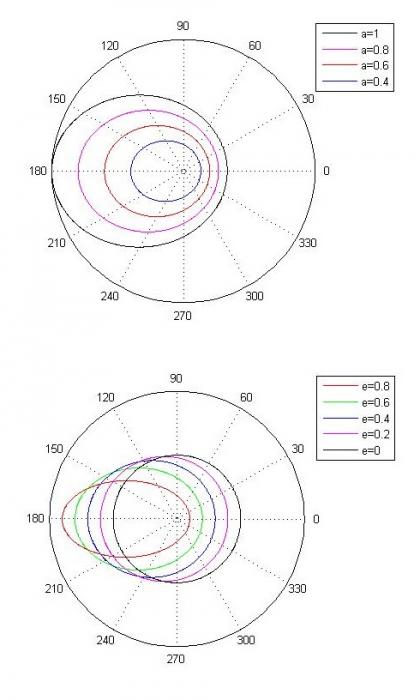
Haut : Effet de la valeur de l'excentricté e sur la forme de l'ellipse
Bas : Effet de la valeur du demi-grand axe a sur la taille de l'ellipse
 Forme des orbites
Forme des orbites
Question 1)
Exprimer la distance étoile-planète lorsque la planète est à son apoastre. Même question lorsqu'elle est située à son périastre .
On a la relation qui donne la distance en fonction de l'angle 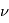 :
: 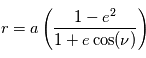
Question 2)
Calculer, en utilisant les données du catalogue des exoplanètes, la valeur munérique de ces deux distances pour l'exoplanète détectée à ce jour, ayant la valeur d'excentricité la plus élevée du catalogue.
Dans le catalogue, classer les planètes par value d'excentricité décroissante pour identifier l'exoplanète recherchée.
Question 3)
Utiliser les données du catalogue des exoplanètes et l'outil histogrammes pour étudier la variabilité des excentricités des exoplanètes.
Estimez l'excentricité moyenne des exoplanètes détectées à ce jour
Tracez l'histogramme des excentricités et pensez à diminuer le nombre de bins de l'histogramme pour obtenir simplement une valeur approchée de la moyenne des excentricités.
Auteur: Valérie Ciarletti
 Dimension des orbites
Dimension des orbites
L'objectif de cet exercice est d'étudier les tailles des ellipses des exoplanètes qui ont été détectées à ce jour en utilisant les données du catalogue et les outils qui permettent de les visualiser.
Question 1)
La taille d'une ellipse est donnée par la valeur de son demi-grand axe a. Pensez à utiliser l'échelle logarithmique.
Question 2)
Utilisez la boite à outils diagrammes pour rechercher un lien entre taille et forme des ellipses.
La deuxième loi de Kepler (1604)
Loi des aires : En un temps donné, le segment qui joint le centre du soleil au centre de la planète en orbite balaie une surface (aire) égale quelle que soit la position de la planète sur l'orbite.
- Dans le cas particulier où l'orbite est un cercle (excentricté
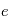 nulle), la distance planète-étoile est constante et la vitesse de déplacement de la planète sur son orbite est constante. On a un mouvement circulaire uniforme.
nulle), la distance planète-étoile est constante et la vitesse de déplacement de la planète sur son orbite est constante. On a un mouvement circulaire uniforme. - Si l'orbite est une ellipse
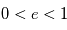 , la distance planète-étoile varie en fonction de la position de la planète sur son orbite, sa vitesse de déplacement également. Plus la planète est proche de son étoile, plus elle va vite.
, la distance planète-étoile varie en fonction de la position de la planète sur son orbite, sa vitesse de déplacement également. Plus la planète est proche de son étoile, plus elle va vite.
Illustration de la loi des aires
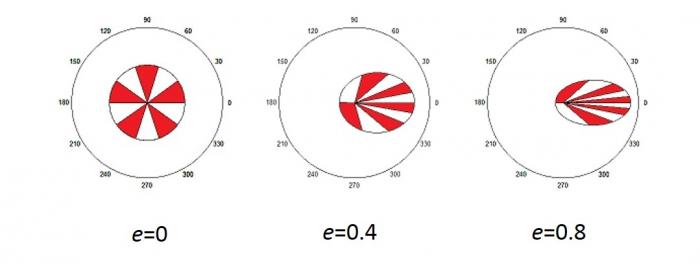
Pour chacun des graphes, le temps de parcours les secteurs colorés ont des aires égales
La troisième loi de Kepler (1618)
Loi des périodes : Le carré de la période de révolution T d'une planète sur son orbite est proportionnel au cube du demi-grand axe de l'ellipse.
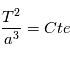
Pour un système planétaire donné, plus une planète est éloignée de son étoile, plus sa période est grande.
Il est important de ne pas tirer de conclusions fausses sur les vitesses relatives de ces planètes. En effet, lorsque les orbites en question ne sont pas des cercles, la vitesse de déplacement de la planète n'est pas constante en accord avec la loi des aires.
Cette loi ayant été établie dans notre système solaire, il pouvait sembler à Kepler que la constante était universelle. Nous verrons par la suite que les lois de la mécanique permettent de calculer cette constante et que la valeur de la constante dépend de la masse de l'étoile. On montre que
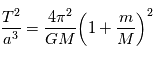
où 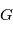 est la constante de gravitation universelle et
est la constante de gravitation universelle et 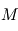 la masse de l'étoile et
la masse de l'étoile et 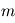 celle de la planète.
celle de la planète.
Dans le cas très fréquent où la masse de l'étoile 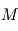 est très supérieure à celle de la planète
est très supérieure à celle de la planète 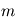 , la relation devient
, la relation devient
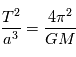 et seule la masse de l'étoile intervient.
et seule la masse de l'étoile intervient.
 Troisième loi de Kepler
Troisième loi de Kepler
Question 1)
Utilisez la boite à outils diagrammes pour représenter pour l'ensemble des exoplanètes du catalogue leur période de révolution autour de son étoile en fonction de la valeur du demi-grand axe de leur ellipse.
Pensez à utiliser les échelles logarithmiques pour mettre en évidence une relation du type 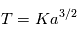
Question 2)
En échelle logarithmique pour les deux axes montrez que les points sont tous sur des droites de même pente.
Expliquez pourquoi, sur le diagramme obtenu, les points ne sont pas tous alignés sur la même droite.
Utiliser le code couleur de l'outil diagramme pour visualiser la masse de l'étoile et vérifier que ce paramètre explique largement le décalage des droites qui sont toutes parallèles.
Mouvement de deux corps sous l'effet de la gravitation
L'attraction gravitationnelle, dans le cas d'un système planète-étoile isolé, permet de démontrer les lois de Kepler et de calculer le mouvement des deux corps. (Ces calculs sont présentés dans la partie comprendre).
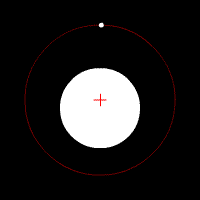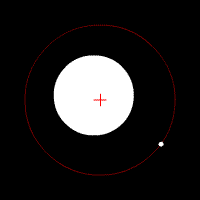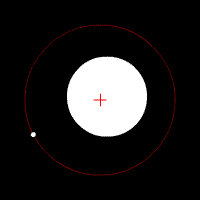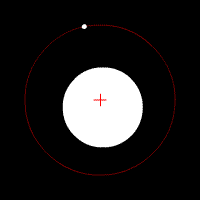
Les animations ci-dessous illustrent l'effet de cette force d'attraction en fonction du rapport des deux masses en jeu. La croix rouge imobile correspond au centre de gravité (barycentre) de l'ensemble.
mouvement de deux corps de même masse
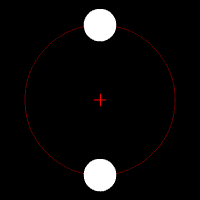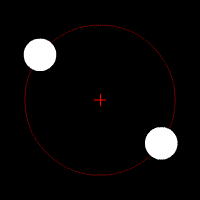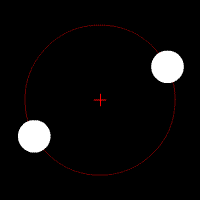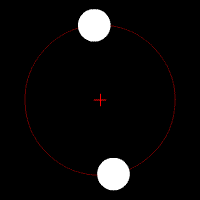
mouvement de deux corps de masse très différente
La Migration des planètes
Au cours de la formation et de l'évolution d'un système planétaire, plusieurs types de migrations planétaires peuvent avoir lieu. On distingue trois types de migration de planètes. Les deux premiers types de migrations ont lieu lorsque la proto-étoile est toujours entourée d'un disque soit de gaz (migration de type I) soit de planétésimaux (migration de type II).
- La migration de type I : elle a lieu lorsqu'une proto-planète d'une masse comparable à la masse terrestre intéragit avec le disque de gaz. La migration s'exerce de l'extérieur vers l'intérieur et fait donc tomber la planète vers son étoile. Cette migration est rapide comparée à la durée de vie du disque
- La migration de type II : elle a lieu lorsque la proto-planète atteint une masse de plus de dix fois celle de la Terre. Elle creuse alors un sillon dans le disque de gaz. Le disque spiralant vers l'étoile va entrainer la proto-planète vers l'astre dans une migration lent comparée à la durée de vie du disque.
Après la dispersion du disque de gaz et de planétésimaux, les planètes peuvent toujours intéragir avec les petits corps rescapés de l'accrétion planétaire. Étant donnée la composition actuelle des planètes Uranus et Neptune (elles contiennent, toutes deux, un coeur solide : signe qu'elles ont du se former plus proche du Soleil), il y a de forts soupçons sur le fait que la migration tardive des planètes du Système solaire soit responsable de l'orbite actuelle d'Uranus et Neptune à, respectivement, 20 et 30 UA du Soleil.
Ces migrations planétaires sont notamment une explication plausible pour l'existence des " Jupiters chauds " : planètes trés massives et trés proches de leur étoile.
Pour en savoir plus sur les migrations planétaires : voir la page en suivant le lien.
Comprendre
Auteur: Valérie Ciarletti
Mouvement d'une planète autour de son étoile - Introduction
Les exoplanètes, comme les planètes et autres corps de notre système solaire sont soumises à loi de la gravitation ou attraction universelle. Cette loi a été historiquement formalisée par Isaac Newton en 1687. Elle permet de modéliser, de façon générale, l'attraction entre des corps ayant une masse et, par conséquent, décrire le mouvement des corps massiques soumis aux forces de gravitation. Dans les pages qui suivent, le principe fondamental de la dynamique est utilisé pour étudié le mouvement de deux corps massiques isolés et démontrer les lois de Kepler.
Le problème à deux corps
On cherche à étudier le mouvement de deux corps de masses 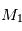 et
et 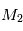 assimilés à deux points matériels localisés aux points
assimilés à deux points matériels localisés aux points 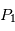 et
et 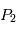 qui sont leur centre de gravité. Le système de ces deux corps étant isolé on fait l'étude dans un référenciel
qui sont leur centre de gravité. Le système de ces deux corps étant isolé on fait l'étude dans un référenciel  supposé Galiléen d'origine arbitraire.
supposé Galiléen d'origine arbitraire.
Lorsque deux corps massiques sont en présence l'un de l'autre, l'effet de la gravitation qui agit sur ces corps se traduit par une force d'attraction. Si ces deux corps sont assimilés à des points matériels localisés en leur centre de gravité, cette force est proportionnelle aux deux masses en jeu et inversement proportionnelle à la distance au carré entre les deux points.
Cette force explique aussi bien la chute des corps sur Terre que le mouvement d'une planète autour de son soleil ou d'une lune autour de sa planète.
L'attraction gravitationnelle
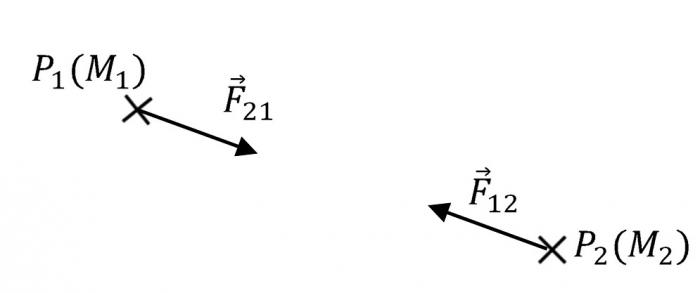
On a la force exercée par  sur
sur  ,
, 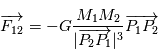 et, par symétrie, la force exercée par
et, par symétrie, la force exercée par 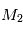 sur
sur 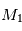 ,
, 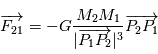
La constante de gravitation universelle est 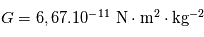
On remarque que 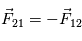 en accord avec la loi de l'action et de la réaction pour un système isolé.
en accord avec la loi de l'action et de la réaction pour un système isolé.
Dans ce référentiel ( ), le principe fondamental de la dynamique appliqué aux deux corps donne donc deux équations couplées
), le principe fondamental de la dynamique appliqué aux deux corps donne donc deux équations couplées
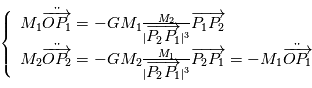
L'objectif est de connaître la position des centres de gravité 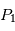 et de
et de 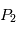 en fonction du temps.
en fonction du temps.
Le choix du référentiel de travail - Réduction à un problème à un corps
Si on considère l'ensemble des deux corps, le centre de gravité (ou barycentre)  est défini de la façon suivante :
est défini de la façon suivante :
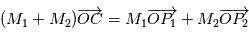
On dérive deux fois par rapport au temps et on utilise le fait que 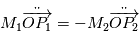 , on obtient alors
, on obtient alors
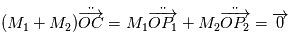
Ce qui traduit le fait que le barycentre  est en mouvement rectligne et uniforme dans le référentiel (
est en mouvement rectligne et uniforme dans le référentiel (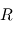 ). Le repère barycentrique (
). Le repère barycentrique (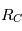 ) dont l'origine est le centre de gravité des deux corps est donc lui aussi Galiléen.
) dont l'origine est le centre de gravité des deux corps est donc lui aussi Galiléen.
On choisit de travailler dans le repère (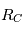 ) ce qui permet de découpler le mouvement du barycentre des mouvements relatifs des deux corps.
) ce qui permet de découpler le mouvement du barycentre des mouvements relatifs des deux corps.
Les équations du mouvement dans le repère barycentrique (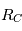 )
)
On note 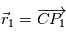 ,
, 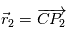
et on introduit 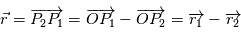
soit 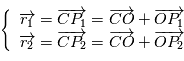
Avec ces notations, les équations du mouvement dans le repère barycentrique deviennent :
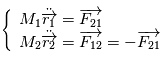
L'expression des forces d'attraction gravitationnelle permet de réécrire ce système sous la forme :
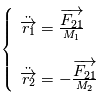 et d'obtenir par différence
et d'obtenir par différence 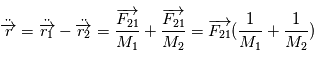
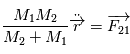
Cette équation peut être interprétée comme l'équation du mouvement d'un corps ponctuel fictif de masse 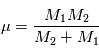 (appeléee masse réduite du système) soumis à la force
(appeléee masse réduite du système) soumis à la force 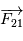 , soit
, soit 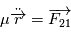 . Dans la suite, ce point fictif sera noté
. Dans la suite, ce point fictif sera noté 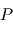 .
.
Le problème à deux corps se réduit donc à un problème à un corps fictif unique. On aboutit à une équation unique pour le mouvement de 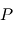 dans laquelle n'apparait que l'inconnue
dans laquelle n'apparait que l'inconnue 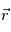 .Cette équation est valable dans le repère baycentrique (
.Cette équation est valable dans le repère baycentrique (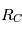 ).
).
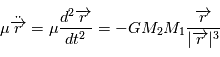
L'expression de la force de gravité permet a priori de modéliser l'interaction entre plusieurs corps (étoiles, planètes, lunes, petits corps ...). Cependant, seul le problème à deux corps peut être mathématiquement résolu sans approximation.
Equation du mouvement lorsque l'étoile est beaucoup plus massive que la planète
Etude du mouvement
Etude du mouvement
Equation de la trajectoire
Exercice sur la trajectoire circulaire
 Exercice
Exercice
Difficulté : ☆☆
Vous vous intéressez à la trajectoire du corps fictif 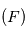 de masse
de masse 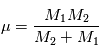 qui est en orbite autour du centre de gravité
qui est en orbite autour du centre de gravité 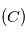 du système isolé planète-étoile, ceci dans le cas particulier d'une orbite circulaire.
du système isolé planète-étoile, ceci dans le cas particulier d'une orbite circulaire.
Question 2)
Exprimer la période 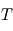 de l'orbite (temps mis par le corps pour parcourir une fois le cercle).Vérifier, toujours dans le cas d'une trajectoire circulaire, la deuxième loi de Kepler.
de l'orbite (temps mis par le corps pour parcourir une fois le cercle).Vérifier, toujours dans le cas d'une trajectoire circulaire, la deuxième loi de Kepler.
La circonférence d'un cercle est égale à 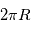 .
.
Question 3)
Dans le cas particulier où ce point est confondu avec le centre de gravité de la planète (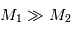 ), simplifier les expressions obtenues précédemment.
), simplifier les expressions obtenues précédemment.
Forme des trajectoires
Evolution de la distance planète-étoile et de la vitesse instantanée le long de l'orbite
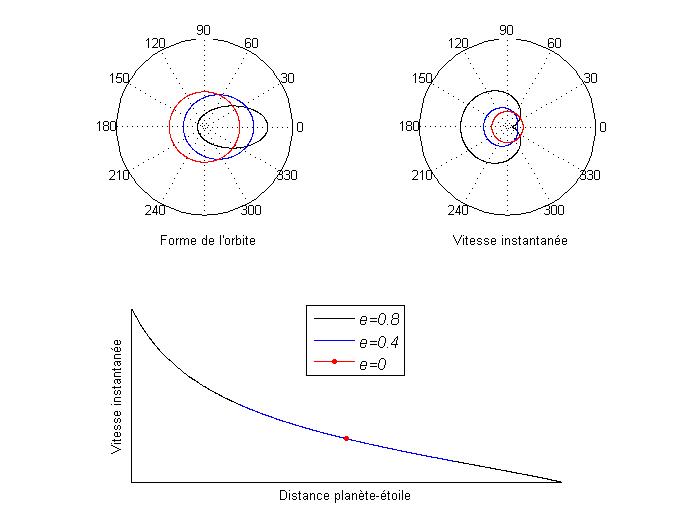
Mise en évidence de l'effet de l'excentricté e sur la vitesse instantanée de déplacement de la planète sur son orbite.
Le cas particulier de l'orbite circulaire est représenté en rouge.
Les animations ci-dessous montrent l'effet de cette force d'attraction en fonction du rapport des deux masses en jeu. La croix rouge imobile correspond au centre de gravité (barycentre) de l'ensemble.
mouvement de deux corps de même masse

mouvement de deux corps de masse très différente

description des orbites
Pour faire les calculs du mouvement d'une planète et de son étoile nous nous avons choisi un repère approprié pour simplifier les calculs (centre du repère au centre de masse, deux axes dans le plan de l'ellipse, ...), il faut maintenant tenir compte du fait que cette ellipse possède une certaine orientation dans l'espace et compléter la liste de paramètres que nous avons pour l'instant.
Une orbite elliptique est décrite au moyen de deux plans (le plan de l'orbite et le plan de référence) et de six paramètres
Description de l'ellipse et du mouvement du corps dans le plan orbital
Plan orbital et mouvement de la planète sur son orbite
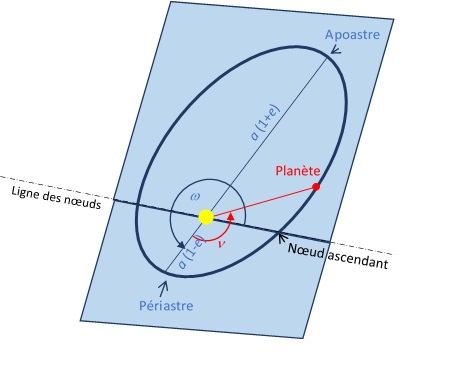
- Le demi-grand axe a donne la taille de l'ellipse. C'est la moitié de la distance entre les deux points les plus éloignés de l'orbite que sont le périastre et l'apoastre
- l'excentricité e donne la forme de cette ellipse.
- L'anomalie
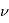 est l'angle polaire qui donne la position de la planète sur son orbite. La valeur
est l'angle polaire qui donne la position de la planète sur son orbite. La valeur  correspond à la direction du point de l'ellipse le plus proche de l'étoile (Le Périastre).
correspond à la direction du point de l'ellipse le plus proche de l'étoile (Le Périastre). - L'orientation de l'orbite dans le plan orbital est donnée par l'argument du périastre
 . Cet angle est défini par rapport à la ligne des noeuds qui est l'intersection du plan orbital avec le plan de référence défini plus loin
. Cet angle est défini par rapport à la ligne des noeuds qui est l'intersection du plan orbital avec le plan de référence défini plus loin
Description du plan orbital
L'orientation du plan orbital est donnée par rapport à un plan de référence.
- Ce plan de référence contient le centre de gravité de l'étoile
- Il contient l'axe vernal qui fait office de direction de référence 'absolue' (même si cette direction n'est pas rigoureusement fixe puisque qu'elle tourne de 360° en presque 30 000 ans). Le plan de l'équateur terrestre coupe le plan de l'écliptique selon une ligne qui passe par le centre de la Terre. On appelle cette ligne la ligne des équinoxes. La direction de cette ligne au moment de l'équinoxe de printemps (21 mars) désigne la direction du point vernal
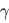 rejeté à l'infini.
rejeté à l'infini.
- L'intersection du plan orbital et du plan de référence forme une ligne que l'on nomme la ligne des noeuds. Le noeud ascendant est le point de l'orbite d'un objet où il traverse le plan de référence depuis l'hémisphère céleste Sud vers l'hémisphère Nord. Le noeud descendant est le point de l'orbite où l'objet traverse le plan de référence de l'hémisphère céleste Nord vers le Sud.
Plan orbital et Plan de référence
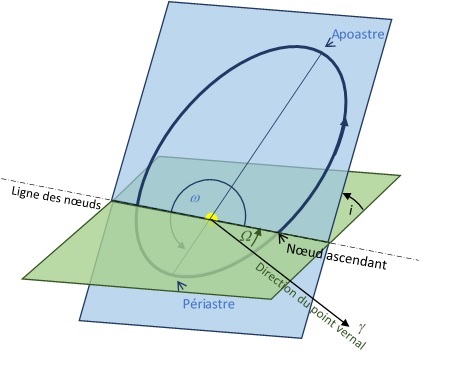
Orientation du plan orbital par rapport au plan de référence
- L'inclinaison i de l'orbite. C'est l'angle entre le plan de l'orbite et le plan de référence.
- La longitude du noeud ascendant
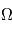 . Le plan de l'orbite coupe le plan de référence en une droite qui est appelée ligne des nœuds. L'orbite coupe donc le plan de référence en deux points qui sont appelés nœuds. Le nœud ascendant est celui par lequel le corps passe en trajectoire ascendante ; l'autre est le nœud descendant.
. Le plan de l'orbite coupe le plan de référence en une droite qui est appelée ligne des nœuds. L'orbite coupe donc le plan de référence en deux points qui sont appelés nœuds. Le nœud ascendant est celui par lequel le corps passe en trajectoire ascendante ; l'autre est le nœud descendant. 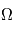 est l'angle, dans le plan de référence, entre la direction du point vernal et celle du neud ascendant
est l'angle, dans le plan de référence, entre la direction du point vernal et celle du neud ascendant - L'argument du périastre
 donne l'orientation de l'axe de l'ellipse dans le plan orbital. C'est l'angle, dans le plan orbital, entre la direction du noeud ascendant et du périastre de l'ellipse.
donne l'orientation de l'axe de l'ellipse dans le plan orbital. C'est l'angle, dans le plan orbital, entre la direction du noeud ascendant et du périastre de l'ellipse.
Méthodes de détection des exoplanètes fondées sur le mouvement
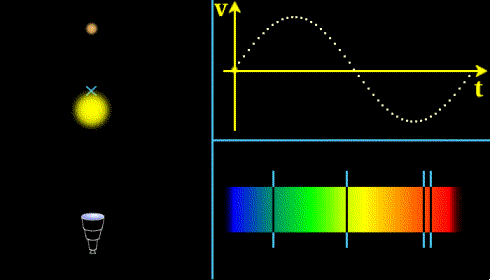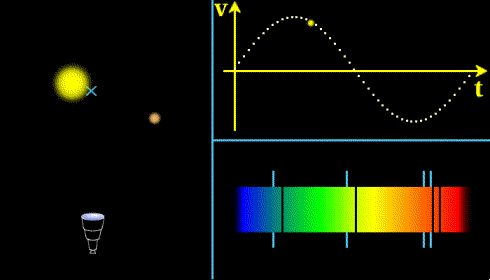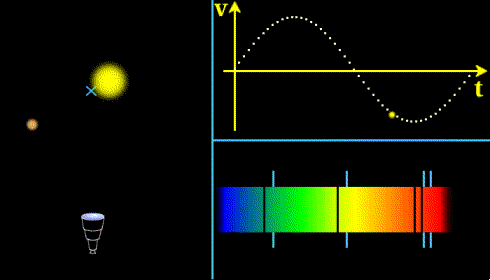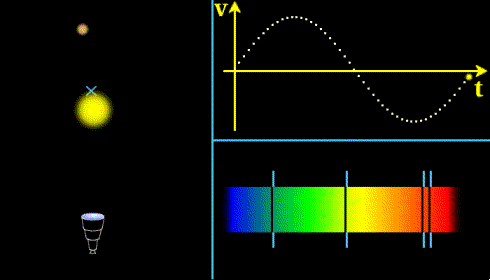
Méthode des transits
le transit désigne le passage d'une planète entre son étoile et nous. L'observation consiste à mesurer la variation du flux stellaire lors de ce passage de façon à obtenir des informations sur la planète étudiée et son orbite. La première planète ainsi découverte est HD209458b en 2000 (Charbonneau et al. 2000).
Le principe est illustré sur la figure ci-dessous. Cette méthode permet de détecter la présence d'une exoplanète en orbite autout de son étoile et d'avoir accès à certains paramètres de l'ellipse. Pour en savoir plus, voir cours sur la méthode de détection des exoplanètes par la méthode des transits.
Illustration du principe de la méthode des transits (crédit CNES)
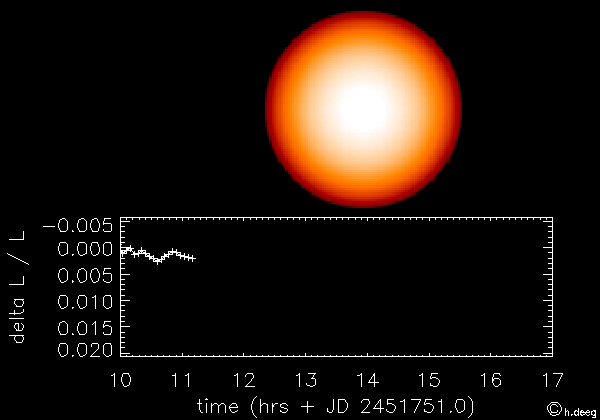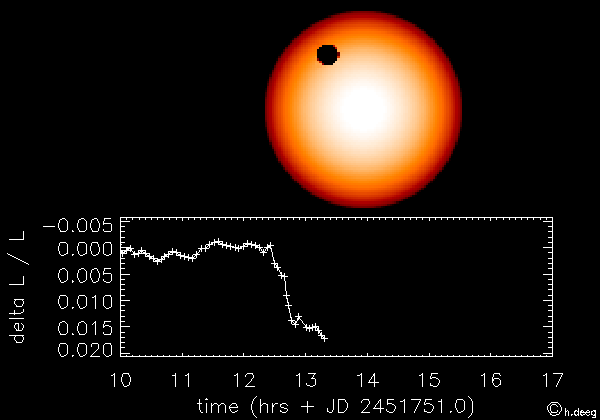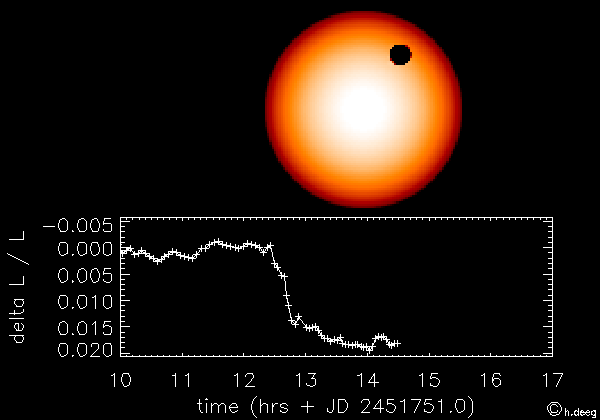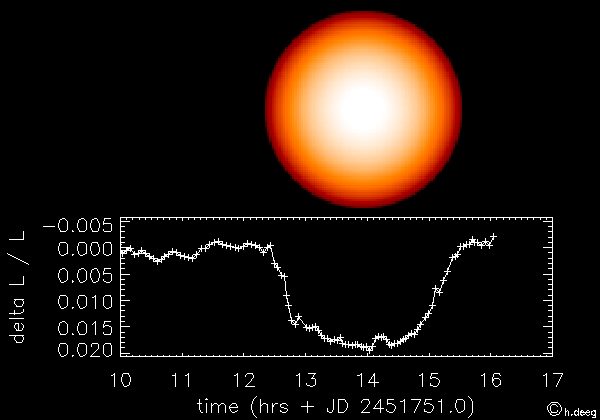
Dans notre système solaire, on peut observer depuis la Terre le transit des planètes Mercure et Vénus qui sont sur des orbites plus proches du soleil que celle de la Terre. Johannes Kepler a été le premier à prédire et pouvoir observer le transit de Mercure en novembre 1631, ainsi que celui de Vénus un mois plus tard.
Méthode des vitesses radiales
Principe : On mesure par effet Doppler la vitesse d'éloignement ou de rapprochement de l'étoile, on peut détecter ainsi qu'il y a une planète en orbite et estimer la période de révolution. Pour en savoir plus,voir cours sur la méthode de détection des exoplanètes par la méthode des vitesses radiales.
Illustration du principe de la méthode des vitesses radiales (crédit CNES)
Problème à N corps
Le cas d'un problème à deux corps, qui a été traité précédemment et qui permet de démontrer les lois de Kepler, est une approximation valable lorsque l'on peut négliger les forces de gravitation dues aux autres corps.
Le problème à N (N>2) corps se pose lorsque N corps massifs interagissent sans que l'on puisse a priori négliger certaines de ces interactions. Dans ce cas, on a un système de N équations à N inconnues qui sont les positions 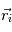 des centres de gravité des N corps de masse
des centres de gravité des N corps de masse 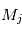 .
.
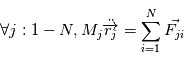
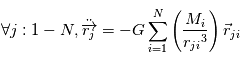 avec
avec 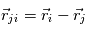
Trouver analytiquement les solutions de ce système d'équations est impossible dans le cas général. Il faut recourir à des méthodes de résolutions approchées (perturbatives ou numériques).
Les points de Lagrange
Dans le cas particulier du problème à trois corps, on s'intéresse ici au mouvement d'un corps 'test' de masse négligeable  qui subit l'attraction de deux corps plus massifs
qui subit l'attraction de deux corps plus massifs et
et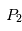 . Le fait que la masse du corps
. Le fait que la masse du corps 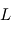 soit négligeable permet de considérer que les mouvements de
soit négligeable permet de considérer que les mouvements de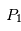 et
et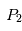 ne sont pas perturbés par la présence de
ne sont pas perturbés par la présence de 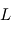 .
.
Pour simplifier la présentation du problème, nous allons nous restreindre au cas où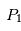 est l'étoile et
est l'étoile et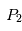 une planète, beaucoup moins massive, est en orbite circulaire autour de son étoile.
une planète, beaucoup moins massive, est en orbite circulaire autour de son étoile.
Le mathématicien Joseph-Louis Lagrange (1772) étudie ce problème. Il montre qu'il existe 5 points, dits de Lagrange (notés 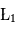 à
à 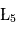 ), pour lesquels les forces d'attraction de
), pour lesquels les forces d'attraction de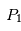 et
et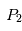 se combinent de façon à ce que le corps "test"
se combinent de façon à ce que le corps "test" 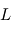 de masse négligeable ait la même période de révolution que les deux autres corps et les suive donc dans leur mouvement autour du centre de gravité de
de masse négligeable ait la même période de révolution que les deux autres corps et les suive donc dans leur mouvement autour du centre de gravité de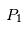 et
et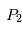 .
.
En contradiction apparente avec les résultats obtenus dans le cadre du problème à deux corps, on peut trouver des corps de masse négligeable qui ont donc une période de révolution égale à celle de la planète mais qui ne sont pas sur la même orbite.
On montre que les points 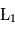 ,
, 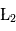 et
et 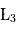 (parfois appelés Points d'Euler) correspondent à des positions instables alors que les points
(parfois appelés Points d'Euler) correspondent à des positions instables alors que les points 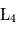 et
et 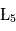 correspondent à des positions stables. Les positions de ces deux derniers points ne dépendent pas des masses des points
correspondent à des positions stables. Les positions de ces deux derniers points ne dépendent pas des masses des points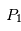 et
et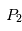 . Dans le cas, du système Soleil/Jupiter, ce sont au voisinage de ces points que se trouvent les nombreux astéroïdes troyens qui suivent (ou précèdent) la révolution de la Terre autour du Soleil. D'autres planètes du système solaire sont suivies ou précédées également par des petits corps troyens (la liste des troyens détectés à ce jour dans notre système solaire est disponible sur le site du Minor Planet Center )
. Dans le cas, du système Soleil/Jupiter, ce sont au voisinage de ces points que se trouvent les nombreux astéroïdes troyens qui suivent (ou précèdent) la révolution de la Terre autour du Soleil. D'autres planètes du système solaire sont suivies ou précédées également par des petits corps troyens (la liste des troyens détectés à ce jour dans notre système solaire est disponible sur le site du Minor Planet Center )
Visualisation des points de Lagrange
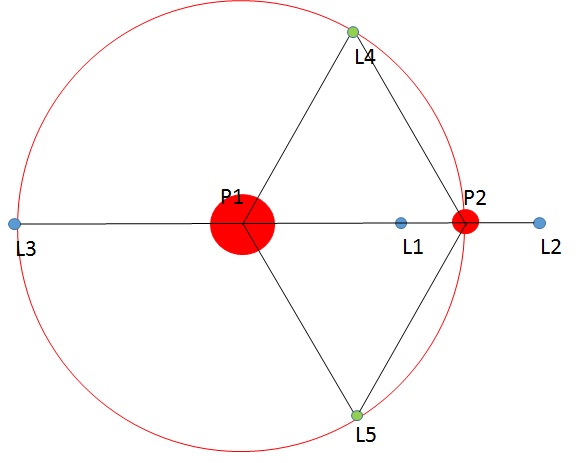
Positions des points de Lagrange pour le système étoile-planète (représentées en rouge). Les points de Lagrange stables sont représentés en vert, les points instables en bleu.
Appliquette Système Solaire 
 Etude par simulation numérique des points de Lagrange
Etude par simulation numérique des points de Lagrange
Vous allez utiliser l'appliquette pour visualiser les points de Lagrange (astéroïdes Troyens) stables et instables d'un système étoile-planète.
Attention : Cette appliquette utilise un système d'unités arbitraire pour les distances, vitesses, masses et temps de façon à ce que les valeurs numériques restent inférieures à un millier.
Question 1)
Choisissez pour commencer le système 'astéroïdes Troyens' proposé par l'appliquette
Laissez évoluer ce système, sans modifier les conditions initiales, jusqu'à 100 unités de temps pour vérifier que les deux petits corps positionnés aux points de Lagrange 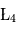 et
et 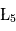 ont bien la même période de révolution autour de l'étoile que la planète.
ont bien la même période de révolution autour de l'étoile que la planète.
Vérifiez qu'initialement les trois corps ont des vitesses très voisines.
Modifiez la masse de l'un des astéroides (de 0.001 à 1 par exemple) et observer le changement qui apparait après un temps suffisamment long d'environ 50 unités. Expliquez ce qui se passe et proposez une explication.
Question 4)
Ajoutez dans le système à deux corps, un point de masse négligeable sur l'axe étoile-planète à la position 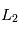 que vous avez précédemment calculée. Donnez à ce petit corps une vitesse initiale quelconque et observez ce que donne la simulation. Etudiez, en prenant quelques valeurs de vitesse différentes, l'impact sur la trajectoire du petit corps. Trouvez une valeur de vitesse initiale qui permet à ce petit corps d'avoir une vitesse angulaire proche de celle de la planète en révolution autour du soleil (au moins pendant une courte durée)
que vous avez précédemment calculée. Donnez à ce petit corps une vitesse initiale quelconque et observez ce que donne la simulation. Etudiez, en prenant quelques valeurs de vitesse différentes, l'impact sur la trajectoire du petit corps. Trouvez une valeur de vitesse initiale qui permet à ce petit corps d'avoir une vitesse angulaire proche de celle de la planète en révolution autour du soleil (au moins pendant une courte durée)
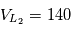 par exemple
par exemple
Question 5)
Reprennez les questions précédentes pour la position 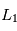 que vous avez calculée.
que vous avez calculée.
Se tester
Auteur: Valérie Ciarletti
Exercices
Pour vérifier que vous avez compris et retenu les notions de base de ce module
Mini Projet
Auteur: Lucie Maquet
Mini Projet
 Masse du trou noir central de la Voie Lactée
Masse du trou noir central de la Voie Lactée
L’observation du centre de notre Galaxie a révélé la présence d’étoiles en orbite autour d’une masse invisible. L’observation de l’étoile S2 autour du centre galactique a été menée sur une dizaine d’années et a ainsi permis de mesurer la masse du corps central invisible. La concentration de masse associée à l’absence de rayonnements visible ou même infrarouge, laisse suspecter la présence d’un trou noir super massif. Dans cette première partie du mini projet, nous vous proposons d’étudier l’orbite de l’étoile S2 et de pouvoir ainsi déterminer la masse du trou noir central.
Appliquette pour le mini-projet 
Question 1)
Pourquoi l'approximation du système à 2 corps semble-t-elle convenable ?
Orbite de S2 autour du trou noir SgrA*
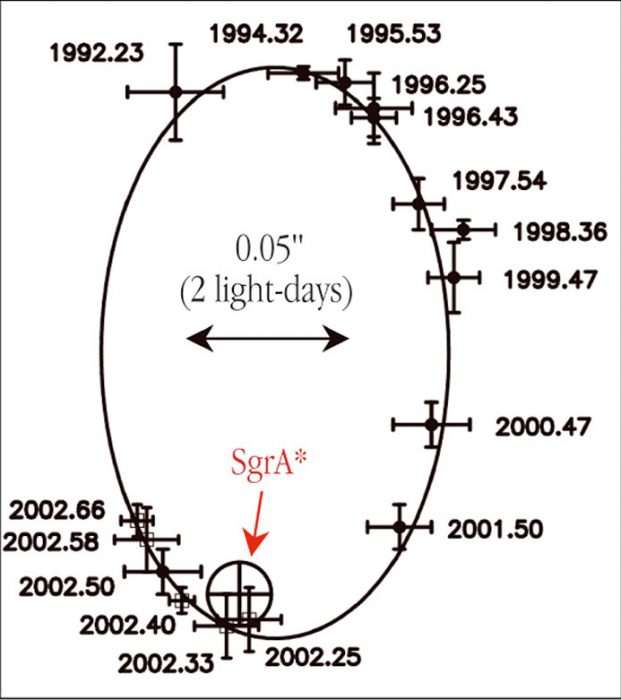
Question 2)
À l'aide de l'appliquette représentant l’orbite projetée dans le plan du ciel de l’étoile ainsi que le trou noir central SgrA*, repérer géométriquement le centre de l’ellipse.
Question 3)
Tracer la projection du grand-axe de l’orbite de S2 et évaluer l’excentricité de l’orbite. (L’excentricité évaluée par le rapport de la distance centre/foyer sur le demi grand axe reste préservée par projection par application du théorème de Thalès)
Question 4)
Lorsque l'étoile S2 est au périastre, elle se situe à une distance angulaire de 0,015". Notre Système solaire étant situé à 8000pc du centre galactique, estimer la distance du périastre au trou noir en unités astronomiques. En déduire le demi-grand axe de l'orbite réelle de l'étoile autour du trou noir en unités astronomiques.
Question 5)
À partir de la figure, déterminer la période de révolution de l'étoile. Grâce aux lois de Kepler, en déduire la masse du trou noir central de notre galaxie (nous sommes dans les conditions ou l'astre central est beaucoup plus massif que l'étoile S2).
 Détermination de la masse de Jupiter grâce aux orbites de ses satellites
Détermination de la masse de Jupiter grâce aux orbites de ses satellites
De la même façon que pour estimer la masse du trou noir central de notre galaxie, il est possible d'estimer la masse de toutes les planètes possèdant un ou plusieurs satellites.
Dans cet exercice, nous allons estimer la masse de Jupiter grâce aux orbites des satellites galiléens (Io, Europe, Ganymède et Callisto). Pour déterminer les positions des satellites par rapport à la planète, nous allons faire appel au serveur d'éphémérides de l'IMCCE.
Question 1)
Déterminez la distance Io-Jupiter pour 6 dates prises à 6h d'intervalle. Pour cela, grâce au serveur d'éphémérides, on se place dans un repére héliocentrique et en coordonnées rectangulaires. On peut ainsi obtenir la position de Io et de Jupiter. Que peut-on en conclure sur la forme de l'orbite du satellite autour de la planète.
Question 2)
Dans la suite de l'exercice, nous ferons l'approximation que l'orbite du satellite est circulaire. On se place à présent dans un repére géocentrique en coordonnées sphériques. Déterminez la distance apparente Jupiter-Io pour une vingtaine de date prise toute les 3h. (Vous pouvez vous servir d'un tableur afin de réaliser les calculs.) La distance Jupiter-Io est comptée positement vers l'ouest et négativement vers l'est.
Question 3)
Tracez cette distance apparente en fonction du temps et déterminer la période de révolution du satellite et le rayon de son orbite. En déduire la masse de Jupiter.
Question 4)
Recommencez l'étude avec les autres satellites galiléens (pensez à échantilloner différemment les dates car les périodes de révolution des satellites sont de plus en plus grandes).
Question 5)
Les masses déterminées avec chacun des satellites sont-elles toujours égales ? D'où viennent ces différences ?
Question 6)
Cet exercice peut aussi être réalisé en observant Jupiter et ses satellites avec un petit télescope ou une lunette et en prenant des clichés de la position du système à intervalle de temps régulier. Pour simuler ces observations, vous pouvez vous appuyer sur le logiciel libre stellarium et effectuer ces mesures à partir de capture d'écran à intervalle de temps régulier.
-------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------
ACCES AU PLAN DES CHAPITRES
Réponses aux QCM
pages_orbite-setester/exercices.html
QCM
'QCM sur les lois de Kepler'
- Question 1
Solution : réponse 1)
- Question 2
Solution : réponse 1)
- Question 3
Aide :
La masse de l'étoile est bien supérieure à celle de la planète mais n'est pas infinie
Solution : réponse 2)
- Question 4
Aide :
Quand la planète est au périastre, elle est au plus proche de l'étoile.
Solution : réponse 1)
Réponses aux exercices
pages_mecanique-orbite/decriretrois.html
Exercice
'Forme des orbites'
- Question 1
Aide :
On a la relation qui donne la distance en fonction de l'angle 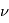 :
: 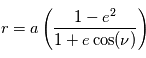
Solution :
Au périastre, 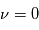 et
et 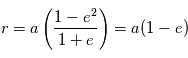 c'est la distance minimale
A l'apoastre,
c'est la distance minimale
A l'apoastre, 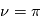 et
et 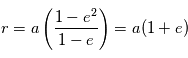 c'est la distance maximale
c'est la distance maximale
- Question 2
Aide :
Dans le catalogue, classer les planètes par value d'excentricité décroissante pour identifier l'exoplanète recherchée.
Solution :
L'exoplanète qui à l'orbite la plus excentrique est HD 20782 b avec une valeur de 0.97.
La valeur de son demi-grand axe a est 1.381 UA.
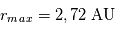
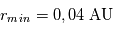
- Question 3
Aide :
Tracez l'histogramme des excentricités et pensez à diminuer le nombre de bins de l'histogramme pour obtenir simplement une valeur approchée de la moyenne des excentricités.
Solution :
L'excentricité moyenne est de 0.18.
pages_mecanique-orbite/decriretrois.html
Exercice
'Dimension des orbites'
- Question 1
Aide :
La taille d'une ellipse est donnée par la valeur de son demi-grand axe a. Pensez à utiliser l'échelle logarithmique.
Solution :
La Terre se situe à 1 AU de son étoile sur une orbite proche d'un cercle. a=1 AU
histogramme demi-grand axe
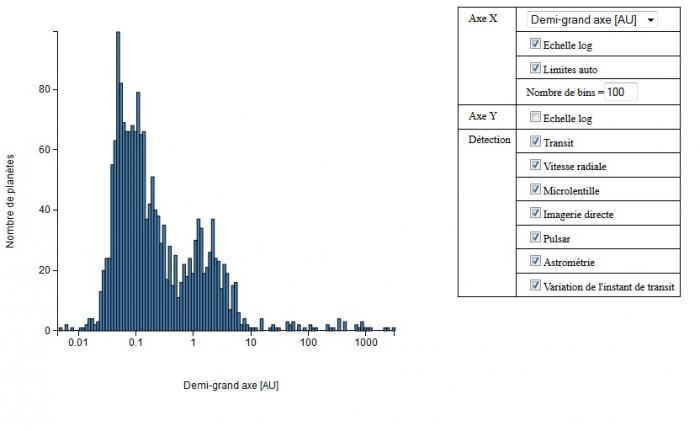
- Question 2
Solution :
Il n'y a pas de corrélation évidente entre ces deux paramètres.
pages_mecanique-orbite/decrirecinq.html
Exercice
'Troisième loi de Kepler'
- Question 1
Aide :
Pensez à utiliser les échelles logarithmiques pour mettre en évidence une relation du type 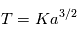
- Question 2
Aide :
Utiliser le code couleur de l'outil diagramme pour visualiser la masse de l'étoile et vérifier que ce paramètre explique largement le décalage des droites qui sont toutes parallèles.
Solution :
Periode en fonction du demi grandaxe en echelle log
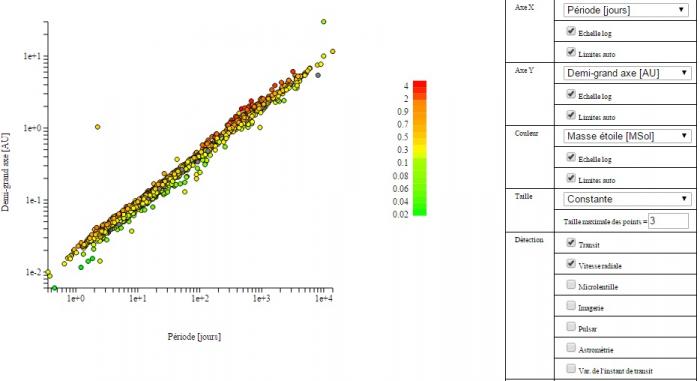
On voit que de façon très globale (malgré quelques points aberrants très évidents en haut à gauche du diagramme), les points correspondant à des planètes autour d'étoiles plus massives (en rouge) ont des periodes de révolution plus grandes que ceux qui (en vert) correspondent à des planètes autour d'étoile moins massives.
En selectionnant des points particuliers on peut vérifier que pour un système donné, les points sont parfaitement alignés sur une droite (exemple du systeme de Kepler 42 avec ses planètes b, c et d en vert)
pages_mecanique-orbite/exercicecirculaire.html
Exercice
pages_mecanique-orbite/lagrange.html
Exercice
'Etude par simulation numérique des points de Lagrange'




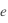 (
( 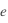 est un nombre sans dimension
est un nombre sans dimension 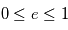 ) qui décrit le degré d'allongement de l'ellipse.
Le cercle est le cas particulier qui correspond à
) qui décrit le degré d'allongement de l'ellipse.
Le cercle est le cas particulier qui correspond à 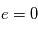 . Le cas particulier
. Le cas particulier 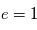 correspond à une parabole (qui ne convient pas pour une orbite fermée mais décrit la chute des corps ).
La trajectoire de la planète sur son orbite est décrite en coordonnées polaires par la relation
correspond à une parabole (qui ne convient pas pour une orbite fermée mais décrit la chute des corps ).
La trajectoire de la planète sur son orbite est décrite en coordonnées polaires par la relation 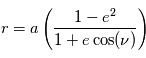 . Sous cette forme, la distance r est mesurée par rapport au centre de l'étoile (qui est sur l'un des foyers) et l'angle polaire
. Sous cette forme, la distance r est mesurée par rapport au centre de l'étoile (qui est sur l'un des foyers) et l'angle polaire 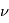 est appelé l'anomalie vraie.
est appelé l'anomalie vraie.
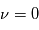 correspond à la direction du point de l'ellipse le plus proche de l'étoile. Cette position qui correspond à la distance planète-étoile minimale est appelée périastre (périhélie pour la Terre qui tourne autour du Soleil). L' apoastre (aphélie dans le cas de la Terre ) est la position qui correspond à la distance planète-étoile maximale.
correspond à la direction du point de l'ellipse le plus proche de l'étoile. Cette position qui correspond à la distance planète-étoile minimale est appelée périastre (périhélie pour la Terre qui tourne autour du Soleil). L' apoastre (aphélie dans le cas de la Terre ) est la position qui correspond à la distance planète-étoile maximale.
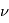 :
: 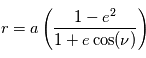
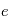 nulle), la distance planète-étoile est constante et la vitesse de déplacement de la planète sur son orbite est constante. On a un mouvement circulaire uniforme.
nulle), la distance planète-étoile est constante et la vitesse de déplacement de la planète sur son orbite est constante. On a un mouvement circulaire uniforme. 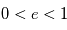 , la distance planète-étoile varie en fonction de la position de la planète sur son orbite, sa vitesse de déplacement également. Plus la planète est proche de son étoile, plus elle va vite.
, la distance planète-étoile varie en fonction de la position de la planète sur son orbite, sa vitesse de déplacement également. Plus la planète est proche de son étoile, plus elle va vite.
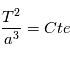
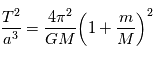
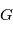 est la constante de gravitation universelle et
est la constante de gravitation universelle et 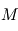 la masse de l'étoile et
la masse de l'étoile et 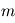 celle de la planète.
celle de la planète.
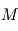 est très supérieure à celle de la planète
est très supérieure à celle de la planète 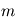 , la relation devient
, la relation devient
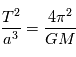 et seule la masse de l'étoile intervient.
et seule la masse de l'étoile intervient.
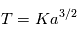


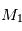 et
et 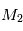 assimilés à deux points matériels localisés aux points
assimilés à deux points matériels localisés aux points 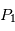 et
et 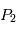 qui sont leur centre de gravité. Le système de ces deux corps étant isolé on fait l'étude dans un référenciel
qui sont leur centre de gravité. Le système de ces deux corps étant isolé on fait l'étude dans un référenciel 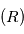 supposé Galiléen d'origine arbitraire.
supposé Galiléen d'origine arbitraire.

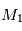 sur
sur 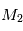 ,
, 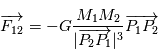 et, par symétrie, la force exercée par
et, par symétrie, la force exercée par 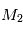 sur
sur 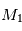 ,
, 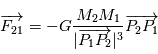
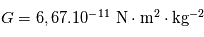
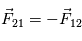 en accord avec la loi de l'action et de la réaction pour un système isolé.
en accord avec la loi de l'action et de la réaction pour un système isolé.
 ), le principe fondamental de la dynamique appliqué aux deux corps donne donc deux équations couplées
), le principe fondamental de la dynamique appliqué aux deux corps donne donc deux équations couplées
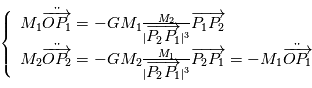
 et de
et de 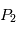 en fonction du temps.
en fonction du temps.
 est défini de la façon suivante :
est défini de la façon suivante :
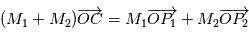
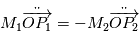 , on obtient alors
, on obtient alors
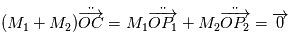
 est en mouvement rectligne et uniforme dans le référentiel (
est en mouvement rectligne et uniforme dans le référentiel (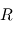 ). Le repère barycentrique (
). Le repère barycentrique (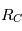 ) dont l'origine est le centre de gravité des deux corps est donc lui aussi Galiléen.
) dont l'origine est le centre de gravité des deux corps est donc lui aussi Galiléen.
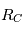 ) ce qui permet de découpler le mouvement du barycentre des mouvements relatifs des deux corps.
) ce qui permet de découpler le mouvement du barycentre des mouvements relatifs des deux corps.
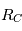 )
)
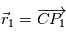 ,
, 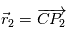
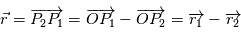
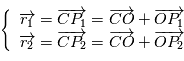
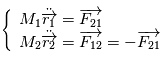
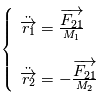 et d'obtenir par différence
et d'obtenir par différence 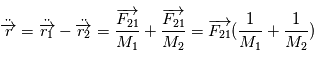
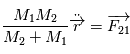
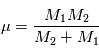 (appeléee masse réduite du système) soumis à la force
(appeléee masse réduite du système) soumis à la force 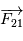 , soit
, soit 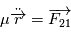 . Dans la suite, ce point fictif sera noté
. Dans la suite, ce point fictif sera noté 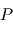 .
.
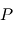 dans laquelle n'apparait que l'inconnue
dans laquelle n'apparait que l'inconnue 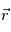 .Cette équation est valable dans le repère baycentrique (
.Cette équation est valable dans le repère baycentrique (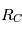 ).
).
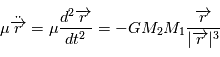
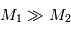
 qui correspond au corps le plus massif est immobile. En effet, la position du centre de gravité est confondue avec celle du corps le plus massif, comme le montre le calcul suivant.
qui correspond au corps le plus massif est immobile. En effet, la position du centre de gravité est confondue avec celle du corps le plus massif, comme le montre le calcul suivant.
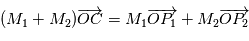 devient
devient 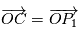
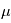 du point
du point  est très voisine de celle
est très voisine de celle  du corps le plus léger.
En effet,
du corps le plus léger.
En effet, 
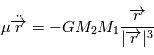 dans le repère barycentrique (
dans le repère barycentrique ( ).
).
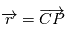 est défini à partir du centre de gravité
est défini à partir du centre de gravité  qui l'origine du repère.
qui l'origine du repère.
 est l'inconnue dont il faut déterminer l'évolution en fonction du temps.
est l'inconnue dont il faut déterminer l'évolution en fonction du temps.
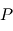 est plane. C'est la première loi de Kepler.
est plane. C'est la première loi de Kepler.
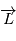 d'un point en mouvement est défini, pour un repère particulier et par rapport à l'origine du repère, de la façon suivante
d'un point en mouvement est défini, pour un repère particulier et par rapport à l'origine du repère, de la façon suivante 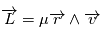 .
Le théorème du moment cinétique (qui se déduit des lois de la mécanique) exprime le fait que la dérivée de ce moment cinétique
.
Le théorème du moment cinétique (qui se déduit des lois de la mécanique) exprime le fait que la dérivée de ce moment cinétique 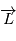 est le produit vectoriel du rayon vecteur
est le produit vectoriel du rayon vecteur 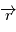 et de la force
et de la force 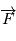 .
.
 ) au point
) au point  , on a donc
, on a donc
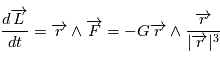 puisque
puisque 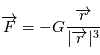
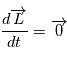 .
. 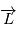 est donc un vecteur constant.
est donc un vecteur constant.
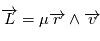 doit être orthogonal à chacun des vecteurs
doit être orthogonal à chacun des vecteurs 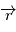 et
et 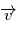 . On montre ainsi que le plan défini en tout instant par les deux vecteurs
. On montre ainsi que le plan défini en tout instant par les deux vecteurs 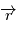 et
et 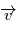 est invariant (orthogonal à l'axe défini par ce vecteur constant
est invariant (orthogonal à l'axe défini par ce vecteur constant  ). C'est le plan dans lequel le point évolue.
). C'est le plan dans lequel le point évolue.
 est bien plane.
est bien plane.
 restait dans un plan fixe qui est perpendiculaire à la direction du moment cinétique constant. Dans ce plan, il est donc possible de décrire le mouvement en coordonnées polaires. l'angle polaire sera noté
restait dans un plan fixe qui est perpendiculaire à la direction du moment cinétique constant. Dans ce plan, il est donc possible de décrire le mouvement en coordonnées polaires. l'angle polaire sera noté 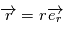 ,
, 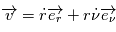 et
et 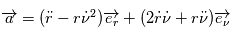
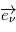 . On a
. On a 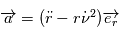
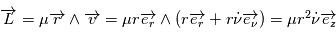 .
.
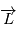 est un vecteur constant, que la quantité
est un vecteur constant, que la quantité 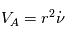 (appelée vitesse aréolaire) reste constante lors du mouvement du corps autour du point
(appelée vitesse aréolaire) reste constante lors du mouvement du corps autour du point  .
.
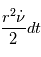 est l'aire balayée pendant la durée dt par le vecteur
est l'aire balayée pendant la durée dt par le vecteur 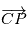 .
.
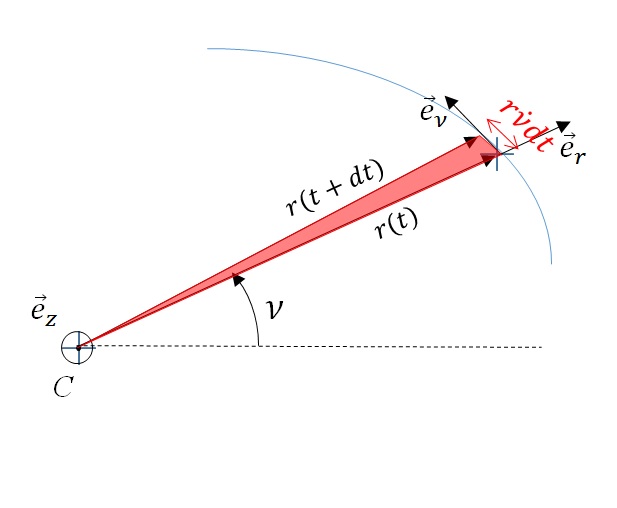
 donné est constante le long de la trajectoire et égale à
donné est constante le long de la trajectoire et égale à  . C'est la loi des aires de Kepler.
. C'est la loi des aires de Kepler.
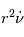 est une constante, alors le signe de
est une constante, alors le signe de 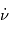 est constant, ce qui traduit le fait que la rotation s'effectue toujours dans le même sens.
est constant, ce qui traduit le fait que la rotation s'effectue toujours dans le même sens.
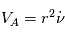 pour exprimer les dérivées de
pour exprimer les dérivées de 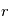 et de
et de 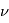 par rapport au temps et réecrire l'accélération du point
par rapport au temps et réecrire l'accélération du point  en introduisant la fonction
en introduisant la fonction 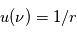 .
.
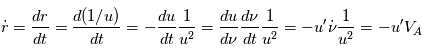 en notant
en notant 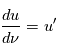
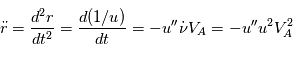 en notant
en notant 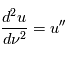
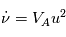
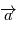 devient alors
devient alors 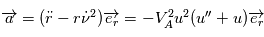 . Cette expression sera utilisée par la suite pour trouver l'équation de la trajectoire du point
. Cette expression sera utilisée par la suite pour trouver l'équation de la trajectoire du point 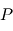 .
.
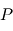 déterminée par les deux variables
déterminée par les deux variables 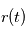 et
et 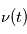 évolue au cours du temps.
Cependant, la résolution de cette équation différentielle, n'est pas possible analytiquement. Nous allons donc nous focaliser sur la relation entre la distance r et l'angle polaire
évolue au cours du temps.
Cependant, la résolution de cette équation différentielle, n'est pas possible analytiquement. Nous allons donc nous focaliser sur la relation entre la distance r et l'angle polaire 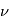 qui modélise la trajectoire du point
qui modélise la trajectoire du point 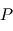 dans le plan de l'orbite.
dans le plan de l'orbite.
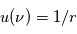 introduite précédemment. Avec cette nouvelle variable, l'équation
introduite précédemment. Avec cette nouvelle variable, l'équation 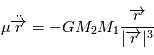 devient
devient
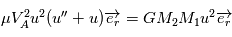
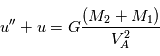
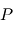
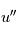 ) à coefficients constants avec second membre constant
) à coefficients constants avec second membre constant 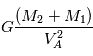 .
.
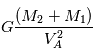 .
.
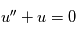 est une fonction sinusoïdale de phase à l'origine et d'amplitude qui dépendent des conditions initiales du problème.
est une fonction sinusoïdale de phase à l'origine et d'amplitude qui dépendent des conditions initiales du problème.
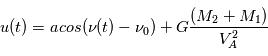 .
.
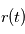 et on obtient l'équation en polaire d'une conique :
et on obtient l'équation en polaire d'une conique :
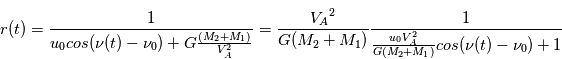
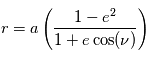 , on a
, on a
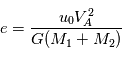 et
et 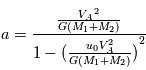
 de masse
de masse 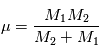 qui est en orbite autour du centre de gravité
qui est en orbite autour du centre de gravité 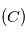 du système isolé planète-étoile, ceci dans le cas particulier d'une orbite circulaire.
du système isolé planète-étoile, ceci dans le cas particulier d'une orbite circulaire.
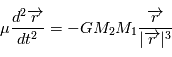 pour montrer que, dans le cas d'une trajectoire circulaire, la vitesse est constante en module sur toute la trajectoire circulaire suivie par le point fictif
pour montrer que, dans le cas d'une trajectoire circulaire, la vitesse est constante en module sur toute la trajectoire circulaire suivie par le point fictif 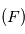 autour du centre de masse des deux corps. Exprimez cette vitesse en fonction du rayon
autour du centre de masse des deux corps. Exprimez cette vitesse en fonction du rayon 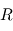 du cercle suivi par
du cercle suivi par 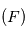 .
.
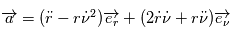 .
Lorsque le mouvement est circulaire
.
Lorsque le mouvement est circulaire 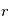 est une constante.
est une constante.
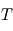 de l'orbite (temps mis par le corps pour parcourir une fois le cercle).Vérifier, toujours dans le cas d'une trajectoire circulaire, la deuxième loi de Kepler.
de l'orbite (temps mis par le corps pour parcourir une fois le cercle).Vérifier, toujours dans le cas d'une trajectoire circulaire, la deuxième loi de Kepler.
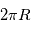 .
.
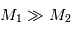 ), simplifier les expressions obtenues précédemment.
), simplifier les expressions obtenues précédemment.


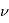 est l'angle polaire qui donne la position de la planète sur son orbite. La valeur
est l'angle polaire qui donne la position de la planète sur son orbite. La valeur 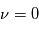 correspond à la direction du point de l'ellipse le plus proche de l'étoile (Le Périastre).
correspond à la direction du point de l'ellipse le plus proche de l'étoile (Le Périastre). 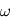 . Cet angle est défini par rapport à la ligne des noeuds qui est l'intersection du plan orbital avec le plan de référence défini plus loin
. Cet angle est défini par rapport à la ligne des noeuds qui est l'intersection du plan orbital avec le plan de référence défini plus loin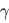 rejeté à l'infini.
rejeté à l'infini.

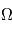 . Le plan de l'orbite coupe le plan de référence en une droite qui est appelée ligne des nœuds. L'orbite coupe donc le plan de référence en deux points qui sont appelés nœuds. Le nœud ascendant est celui par lequel le corps passe en trajectoire ascendante ; l'autre est le nœud descendant.
. Le plan de l'orbite coupe le plan de référence en une droite qui est appelée ligne des nœuds. L'orbite coupe donc le plan de référence en deux points qui sont appelés nœuds. Le nœud ascendant est celui par lequel le corps passe en trajectoire ascendante ; l'autre est le nœud descendant. 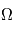 est l'angle, dans le plan de référence, entre la direction du point vernal et celle du neud ascendant
est l'angle, dans le plan de référence, entre la direction du point vernal et celle du neud ascendant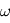 donne l'orientation de l'axe de l'ellipse dans le plan orbital. C'est l'angle, dans le plan orbital, entre la direction du noeud ascendant et du périastre de l'ellipse.
donne l'orientation de l'axe de l'ellipse dans le plan orbital. C'est l'angle, dans le plan orbital, entre la direction du noeud ascendant et du périastre de l'ellipse.

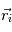 des centres de gravité des N corps de masse
des centres de gravité des N corps de masse 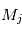 .
.
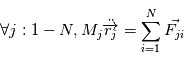
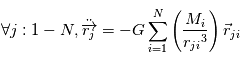 avec
avec 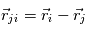
 qui subit l'attraction de deux corps plus massifs
qui subit l'attraction de deux corps plus massifs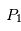 et
et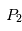 . Le fait que la masse du corps
. Le fait que la masse du corps 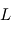 soit négligeable permet de considérer que les mouvements de
soit négligeable permet de considérer que les mouvements de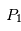 et
et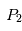 ne sont pas perturbés par la présence de
ne sont pas perturbés par la présence de 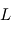 .
.
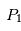 est l'étoile et
est l'étoile et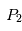 une planète, beaucoup moins massive, est en orbite circulaire autour de son étoile.
une planète, beaucoup moins massive, est en orbite circulaire autour de son étoile.
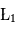 à
à 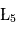 ), pour lesquels les forces d'attraction de
), pour lesquels les forces d'attraction de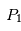 et
et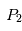 se combinent de façon à ce que le corps "test"
se combinent de façon à ce que le corps "test" 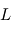 de masse négligeable ait la même période de révolution que les deux autres corps et les suive donc dans leur mouvement autour du centre de gravité de
de masse négligeable ait la même période de révolution que les deux autres corps et les suive donc dans leur mouvement autour du centre de gravité de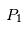 et
et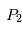 .
.
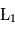 ,
, 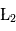 et
et 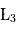 (parfois appelés Points d'Euler) correspondent à des positions instables alors que les points
(parfois appelés Points d'Euler) correspondent à des positions instables alors que les points 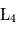 et
et 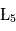 correspondent à des positions stables. Les positions de ces deux derniers points ne dépendent pas des masses des points
correspondent à des positions stables. Les positions de ces deux derniers points ne dépendent pas des masses des points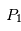 et
et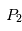 . Dans le cas, du système Soleil/Jupiter, ce sont au voisinage de ces points que se trouvent les nombreux astéroïdes troyens qui suivent (ou précèdent) la révolution de la Terre autour du Soleil. D'autres planètes du système solaire sont suivies ou précédées également par des petits corps troyens (la liste des troyens détectés à ce jour dans notre système solaire est disponible sur le site du
. Dans le cas, du système Soleil/Jupiter, ce sont au voisinage de ces points que se trouvent les nombreux astéroïdes troyens qui suivent (ou précèdent) la révolution de la Terre autour du Soleil. D'autres planètes du système solaire sont suivies ou précédées également par des petits corps troyens (la liste des troyens détectés à ce jour dans notre système solaire est disponible sur le site du 

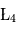 et
et 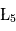 ont bien la même période de révolution autour de l'étoile que la planète.
ont bien la même période de révolution autour de l'étoile que la planète.
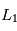 et
et 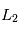 (situés de part et d'autre de la planète sur l'axe entre la planète et l'étoile).
(situés de part et d'autre de la planète sur l'axe entre la planète et l'étoile).
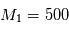 ,
, 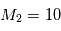 ,
, 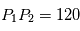 ,
, 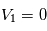 . Trouver (en tâtonnant) une valeur de la vitesse initiale qui permet d'avoir une orbite quasi-circulaire pour la planète. Vérifiez que l'orbite de
. Trouver (en tâtonnant) une valeur de la vitesse initiale qui permet d'avoir une orbite quasi-circulaire pour la planète. Vérifiez que l'orbite de 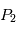 autour de
autour de  est voisine d'une orbite circulaire.
est voisine d'une orbite circulaire.
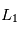 et
et 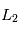
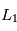 et
et 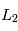 .
.
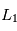 et
et 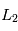 par rapport au centre de masse
par rapport au centre de masse  du système étoile-planète sont données par les développements limités suivants:
du système étoile-planète sont données par les développements limités suivants:
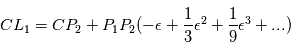 et
et 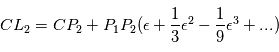
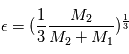
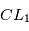 et
et 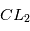 pour la configuration que vous allez simuler.
pour la configuration que vous allez simuler.
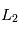 que vous avez précédemment calculée. Donnez à ce petit corps une vitesse initiale quelconque et observez ce que donne la simulation. Etudiez, en prenant quelques valeurs de vitesse différentes, l'impact sur la trajectoire du petit corps. Trouvez une valeur de vitesse initiale qui permet à ce petit corps d'avoir une vitesse angulaire proche de celle de la planète en révolution autour du soleil (au moins pendant une courte durée)
que vous avez précédemment calculée. Donnez à ce petit corps une vitesse initiale quelconque et observez ce que donne la simulation. Etudiez, en prenant quelques valeurs de vitesse différentes, l'impact sur la trajectoire du petit corps. Trouvez une valeur de vitesse initiale qui permet à ce petit corps d'avoir une vitesse angulaire proche de celle de la planète en révolution autour du soleil (au moins pendant une courte durée)
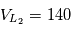 par exemple
par exemple
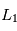 que vous avez calculée.
que vous avez calculée.

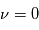 et
et 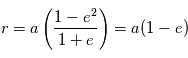 c'est la distance minimale
A l'apoastre,
c'est la distance minimale
A l'apoastre, 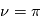 et
et 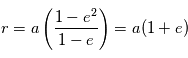 c'est la distance maximale
c'est la distance maximale
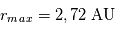
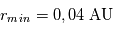


 subie par le point
subie par le point 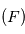 est colinéaire à
est colinéaire à 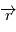 du fait de la force centrale et ne dépend que de
du fait de la force centrale et ne dépend que de 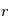 .
Pour un mouvement circulaire, on a de plus
.
Pour un mouvement circulaire, on a de plus 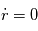 , la force est constante en module.
, la force est constante en module.
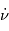 .est une constante, le mouvement circulaire est donc obligatoirement uniforme.
La vitesse est égale à ,
.est une constante, le mouvement circulaire est donc obligatoirement uniforme.
La vitesse est égale à , 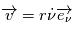
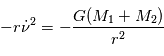 d'où
d'où 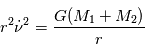 D'ou la relation
D'ou la relation 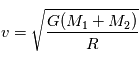 .
Il est également possible de faire le calcul de cette vitesse est d'utiliser la conservation de l'énergie mécanique : cinétique + potentielle de gravitation.
.
Il est également possible de faire le calcul de cette vitesse est d'utiliser la conservation de l'énergie mécanique : cinétique + potentielle de gravitation.
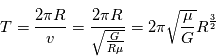 .
. 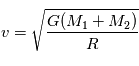 .
C'est la troisième loi de Kepler qui dit que
.
C'est la troisième loi de Kepler qui dit que 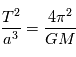
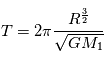 et
et 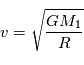 .
.
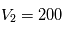 convient.
convient.
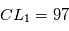 et
et 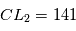
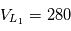 par exemple
par exemple