 Datation de la météorite «Allende»
Datation de la météorite «Allende»
La météorite dite « Allende », tombée en 1969 au Mexique, est probablement la météorite la plus étudiée de toute l’histoire. Elle est le représentant archétypal des chondrites carbonées, qui sont parmi les corps les plus primitifs du système solaire (cf. lien). Elle a de ce fait fortement contribué à faire connaître l’âge de notre système solaire à une très grande précision.
La méthode utilisée pour cette datation se base sur la désintégration U-Pb et sur la mesure des abondances relatives des différents isotopes du plomb.
Question 1)
La Figure présente les différentes mesures isotopiques effectuées en différents endroits de la météorite. En vous basant sur ce graphe, essayez d’estimer l’âge « d’Allende » en utilisant les formules présentées au chapitre «Comprendre ».
Attention: Les fractions isotopiques reportées sur le graphe ne sont pas forcément celles de la formule présentée dans le cours.
 Reconstruire la nébuleuse solaire de masse minimale (MMSN)
Reconstruire la nébuleuse solaire de masse minimale (MMSN)
La MMSN est une entité théorique qui permet d’avoir une idée de la structure initiale du disque proto-planétaire qui a formé les planètes du système solaire, en faisant l’hypothèse que celles-ci se sont, en gros, formées à leur emplacement actuel (cf. cours).
Question 1)
A partir de la masse et de la composition actuelle des 8 planètes du système solaire, donner une estimation de la distribution radiale de la matière solide (roches+ glaces) dans la MMSN. Pour cela on peut supposer que la masse solide de toutes les planètes était initialement repartie dans un disque continu s’étendant de l’orbite de Mercure à celle de Neptune. L'information que l'on cherche est alors quelle est la densité surfacique ∑de matière (par exemple en kg/m2) dans ce disque en fonction de la distance radiale r au soleil. Il peut ensuite être intéressant de tracer un graphe représentant ∑(r).
Attention: si pour les planètes telluriques la masse solide de ces planètes peut-être considérée comme étant égale à leur masse totale, il n'en va pas de même pour les planètes géantes (qui contiennent également beaucoup de gaz). La masse totale de matière solide (roche+glaces) contenue dans les planètes géantes n'est pas connue avec une grande précision, mais on pourra prendre les fourchettes suivantes:
Jupiter: entre 10 et 45 MTerre de matière solide
Saturne: entre 20 et 30MTerre de matière solide
Uranus: entre 9 et 13 MTerre de matière solide
Jupiter: entre 12 et 16 MTerre de matière solide
On peut considérer que la masse de chaque planète était initialement uniformément répartie entre la moitié de la distance jusqu'à la planète précédante (plus proche du Soleil) et la moitié de la distance jusqu'à la planète suivante (plus éloignée du Soleil). Dans ce cas, on peut facilement estimer la densité surfacique moyenne de matière dans l'anneau défini par ces 2 limites.
Attention: On prendra en compte la ceinture d'astéroides, en considérant que la masse totale de celle-ci (environ 1022kg) se situe à une distance moyenne de 3UA du soleil.
 Croissance «ordonnée» d'une population de planétésimaux
Croissance «ordonnée» d'une population de planétésimaux
Comme nous l’avons vu (cf. lien1 et lien2 ), l’étape intermédiaire dans le scénario de formation planétaire est celle qui fait passer de planétésimaux kilométriques à des « embryons » planétaires de 500-1000km. Lors de cette étape, le processus fondamental est l’attraction gravitationelle mutuelle des planétésimaux lors de leurs rencontres. Dans sa version initiale, le modèle d’accrétion des planétésimaux supposait que ceux-ci croissent de manière « ordonnée », c’est à dire tous ensemble et à la même vitesse. Même si on sait qu’aujourd’hui ce scénario ne correspond pas à la réalité (l’accrétion se faisant par effet « boule de neige » bien plus rapide), il est quand même intéressant d’avoir une idée du rythme de croissance pour cette croissance « ordonnée ».
 Vidage de la zone d'alimentation des embryons
Vidage de la zone d'alimentation des embryons
Les phases d’accrétion boule-de-neige puis oligarchique produisent in fine un seul corps dominant (un « embryon ») à chaque distance radiale de l’étoile centrale (cf. cours « Accretion boule de neige », « Oligarchique » et « épuisement des ressources »). Un tel corps grossit en accrétant des petits planétésimaux et débris contenus dans sa « zone d’alimentation », c’est à dire un anneau radial à l’intérieur duquel tout corps aura une orbite croisant celle du corps dominant en raison de la focalisation gravitationnelle vers celui-ci (cf. lien). Pour un corps massif, la largeur de cette zone d’alimentation est environ égale à 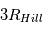 de chaque côté de l'orbite de la planète, où
de chaque côté de l'orbite de la planète, où 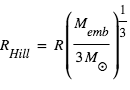 est le rayon de Hill correspondant à la « sphère d’influence » gravitationnelle du corps.
est le rayon de Hill correspondant à la « sphère d’influence » gravitationnelle du corps.
Question 1)
A) Montrer que la croissance par accrétion sur l’embryon va forcément finir par s’arrêter, car l’élargissement de la zone d’alimentation est plus lent que la croissance de l’embryon.
B) Estimer, pour une MMSN à 1UA du soleil, quelle est approximativement la masse atteinte par un embryon au moment où sa zone d’alimentation est vidée.
Ceci revient, en pratique, à comparer, pour une masse 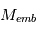 donnée, la masse totale disponible dans la zone d’alimentation à la masse de l’embryon lui même.
donnée, la masse totale disponible dans la zone d’alimentation à la masse de l’embryon lui même.
 Datation de la météorite «Allende»
Datation de la météorite «Allende»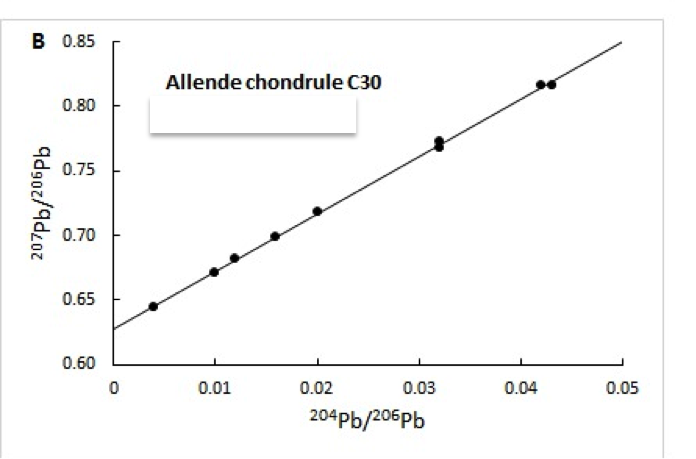
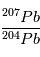 et
et 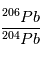 . Si tout se passe bien, on obtiendra alors une valeur pour le rapport
. Si tout se passe bien, on obtiendra alors une valeur pour le rapport 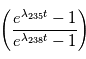 . Il n'y a hélas pas de solution analytique à cette équation. Pour trouver la valeur de t, on pourra s'aider d'un solveur numérique, comme par exemple
. Il n'y a hélas pas de solution analytique à cette équation. Pour trouver la valeur de t, on pourra s'aider d'un solveur numérique, comme par exemple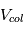 sont de l’ordre des vitesses de libération
sont de l’ordre des vitesses de libération 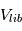 (attention :
(attention : 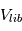 va donc évoluer au cours du temps, car cette vitesse est directement proportionnelle à la taille des planétésimaux)
va donc évoluer au cours du temps, car cette vitesse est directement proportionnelle à la taille des planétésimaux)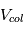 peut alors facilement s’exprimer en fonction de l’excentricité des orbites (voir cours).
peut alors facilement s’exprimer en fonction de l’excentricité des orbites (voir cours).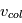 dans un disque d’épaisseur
dans un disque d’épaisseur 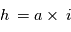 (où a est la distance au soleil eti est l'inclinaison des orbites de tous les planétésimaux)
(où a est la distance au soleil eti est l'inclinaison des orbites de tous les planétésimaux)
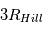 de chaque côté de l'orbite de la planète, où
de chaque côté de l'orbite de la planète, où 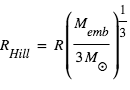 est le rayon de Hill correspondant à la « sphère d’influence » gravitationnelle du corps.
est le rayon de Hill correspondant à la « sphère d’influence » gravitationnelle du corps.
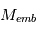 donnée, la masse totale disponible dans la zone d’alimentation à la masse de l’embryon lui même.
donnée, la masse totale disponible dans la zone d’alimentation à la masse de l’embryon lui même.