Rayon
Géométrie des transits
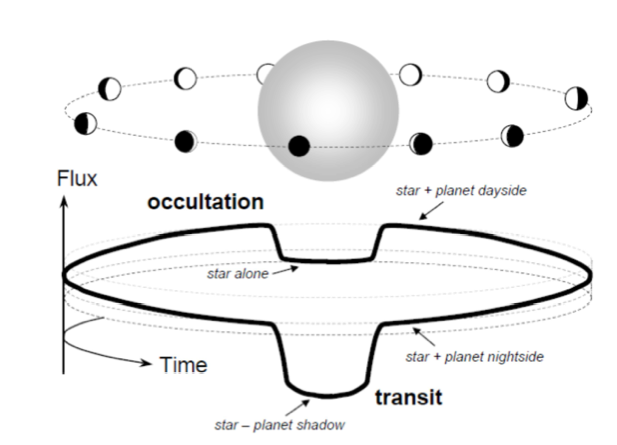
Figure 1 : Géométrie de l’orbite d’une planète transitante. Nous utilisons ici le terme éclipse secondaire pour désigner le passage de la planète derrière l’étoile, i.e. l’occultation.
Crédit :
A traduire
La figure ci-jointe montre schématiquement la géométrie d’observation d’une exoplanète transitante. L’observable la plus directe est la mesure de la variation de flux pendant le transit primaire et l'éclipse secondaire. Hors transit, le flux mesuré correspond à la somme du flux de l’étoile 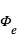 et celui de la planète
et celui de la planète 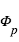 . Pendant l'éclipse secondaire, le flux mesuré est restreint à
. Pendant l'éclipse secondaire, le flux mesuré est restreint à 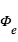 .
.
Pendant le transit primaire, une fois que la planète est entièrement devant le disque de l’étoile, une fraction de la surface de l'étoile est cachée, 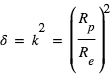 , où
, où 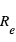 et
et 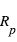 sont respectivement le rayon de l'étoile et de la planète. Le flux de lumière de l'étoile est réduit d'une fraction δ. Comme la planète est devant l’étoile, elle nous présente sa face non-éclairée, donc sa contribution au flux observé est nulle. En conséquence, le rapport du flux mesuré pendant le transit primaire à celui mesuré pendant l'éclipse secondaire (ou en pratique à celui mesuré à n’importe quel moment hors du transit) donne directement le rapport du rayon de la planète à celui de l’étoile.
sont respectivement le rayon de l'étoile et de la planète. Le flux de lumière de l'étoile est réduit d'une fraction δ. Comme la planète est devant l’étoile, elle nous présente sa face non-éclairée, donc sa contribution au flux observé est nulle. En conséquence, le rapport du flux mesuré pendant le transit primaire à celui mesuré pendant l'éclipse secondaire (ou en pratique à celui mesuré à n’importe quel moment hors du transit) donne directement le rapport du rayon de la planète à celui de l’étoile.
 Transit de planètes du système solaire
Transit de planètes du système solaire
Question 1)
Calculez la baisse de luminosité du Soleil dû à un transit de Jupiter, de la Terre.
Les petites étoiles favorisent la détection de transits
L'exercice ci-dessus montre que le transit de Jupiter devant le Soleil conduit à une baisse de luminosité de celui-ci de 1.05%. Pour la Terre passant devant le Soleil, l’assombrissement relatif n’est que de 0.0084%.
La perte de flux mesurée pendant l'éclipse secondaire dépend elle non seulement du rapport 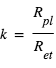 , mais également du rapport de l’intensité lumineuse spécifique (i.e. pour une surface donnée) émise par les deux objets. Comme on le verra plus loin, il dépend de de la longueur d’onde, et selon celle-ci, des températures de la planète et de l’étoile, ou de l’albédo de la planète.
, mais également du rapport de l’intensité lumineuse spécifique (i.e. pour une surface donnée) émise par les deux objets. Comme on le verra plus loin, il dépend de de la longueur d’onde, et selon celle-ci, des températures de la planète et de l’étoile, ou de l’albédo de la planète.
L’expression de la perte de flux au moment du transit montre que la détection d’un transit d’une exoplanète de rayon donné autour d’une étoile naine (de type M) est plus favorable qu’autour d’une étoile de type solaire ou d’une étoile géante. Par exemple, l’étoile Kepler- 42 a un rayon égal à 0.17 rayon solaire (120 000 km). Elle abrite 3 planètes, dont la plus petite (Kepler-42 d), a un rayon de ∼0.57 rayon terrestre, ce qui donne un signal photométrique de l’ordre de 0.1%, plus de dix fois plus fort que la Terre devant le Soleil.
La grande puissance de la méthode des transits résulte de la reproductibilité du phénomène. Un système transitant peut être observé autant de fois que l’on souhaite, avec à chaque fois les mêmes caractéristiques en termes de timing et de profondeur de transit, ce qui permet l’accumulation de la précision sur ces deux paramètres. La précision sur la mesure des instants de transits est riche d’enseignements.
Dans le cas d’une orbite circulaire de période P, un transit et l'éclipse secondaire adjacente sont séparés temporellement de P/2. Ce n’est plus le cas pour une orbite elliptique, et la mesure de ces séparations temporelles (transit-éclipse et éclipse-transit) donne une information sur l’excentricité de l’orbite; plus précisément, elle contraint le produit e cos (ω), où e est l’excentricité et ω l’argument du périastre.
La mesure des durées relatives du transit et de l'éclipse secondaire fournissent aussi des contraintes sur ces paramètres, mais avec moins de précision, eu égard à la courte durée des transits par rapport à leur périodicité.
Au-delà même de la caractérisation statistique des orbites planétaires, l’intérêt physique de ces mesures d’excentricité est grand. Ainsi, pour les planètes proches de leur étoile, les effets de marée associés aux orbites elliptiques produisent un chauffage interne qu’il est possible d’estimer, fournissant des contraintes sur la structure thermique des objets.
Par ailleurs, s’agissant de la connaissance de la période orbitale et des instants de transit et d’éclipse, la méthode des transits est presque toujours plus précise que la méthode des vitesses radiales. Pour autant, ces paramètres interviennent dans l’interprétation des courbes de vitesse radiale (ce sont 3 des 6 paramètres libres associés à cette méthode), donc leur connaissance indépendante via les transits a un grand intérêt pour l’amélioration de la précision sur les autres.
Orientation de l'orbite
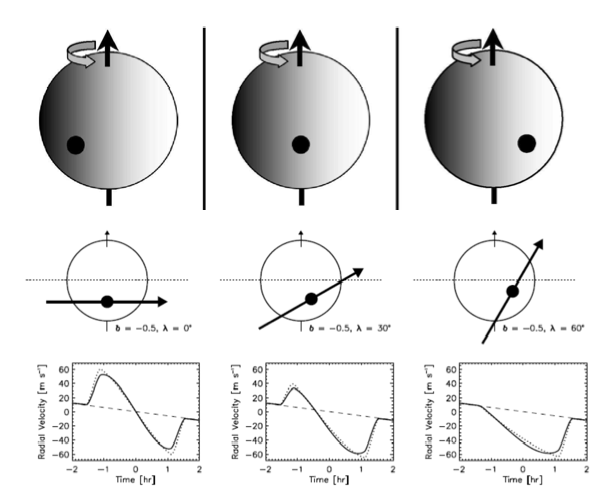
Figure 2 : Transit d’une exoplanète en présence de rotation stellaire. La planète masque d’abord des régions émettant vers le bleu, puis vers le rouge. La dernière ligne montre l’évolution de la vitesse radiale mesurée pour l’étoile pour différentes orientations de l’orbite planétaire. Dans les trois situations montrées, la durée du transit est la même de sorte que la simple observation photométrique du transit ne pourrait les distinguer.
Crédit :
A traduire
Une exoplanète qui transite devant son étoile possède une orientation favorable pour la spectroscopie des vitesses radiales : L'étoile et la planète tournent autour de leur centre de gravité. Au moment du transit planétaire, l'étoile est à son point le plus éloigné de la Terre (i.e. l'observateur) et sa vitesse Doppler s'annule.
S’y rajoute un effet subtil : en raison de sa rotation propre, le rayonnement d’une partie de l’étoile est décalé vers le bleu, l’autre vers le rouge (Fig. 2). Si la planète a une orbite prograde (dans le même sens que la rotation stellaire), elle masque d’abord des régions de l’étoile émettant un rayonnement décalé vers le bleu (zones grisées sur la Fig. 2), puis vers le rouge (zones claires). En conséquence, par rapport à sa valeur mesurée au centre du transit, la vitesse radiale globale de l’étoile est d’abord décalée vers le rouge, puis vers le bleu. C’est ce que l’on appelle l’effet Rossiter- McLaughlin. L’effet est loin d’être faible: en raison des fortes vitesses de rotation stellaires (typiquement 2 km/s pour le Soleil), il peut se chiffrer en quelques dizaines de mètre par seconde – soit souvent plus que la vitesse Doppler de l’étoile liée à la planète.
L’évolution du décalage Doppler de l’étoile pendant le transit permet alors non seulement de confirmer l’existence du transit, mais aussi de déterminer l’orientation de l’orbite planétaire, à savoir l’angle entre le plan orbital et l’axe de rotation de l’étoile (angle appelé obliquité de l’étoile).
Cette méthode a mis en évidence de nombreux cas de tels désalignements spin-orbite, voire d’orbites planétaires rétrogrades. L’origine de ces désalignements reste mal comprise, mais est sans doute liée à des phénomènes d’interaction, magnétique entre la jeune étoile et le disque proto-stellaire, ou gravitationnelle avec des compagnons stellaires au moment de la formation, qui auraient pu faire « basculer » l’axe de rotation stellaire. Une autre hypothèse serait que l’axe de rotation de l’étoile représente bien la direction perpendiculaire au plan du disque primordial, et que c’est le système planétaire dont le plan orbital a changé depuis sa formation.
Orbites non kepleriennes et planètes additionnelles
TTV
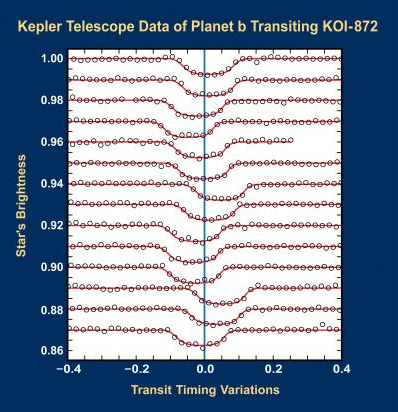
TTV de l'étoile KOI 872 (Kepler-46)
Crédit :
D. Forgan
Kepler-88

La planète Kepler-88b transite devant l'étoile Kepler-88. La planète Kepler-88c a été décourverte par les perturbations induites sur les instants des transits.
Crédit :
A. Santerne
De manière encore plus fine, la précision extraordinaire qui peut être atteinte sur les instants de transits peut révéler des cas d’orbites non-képleriennes. Ces situations peuvent résulter d’effets relativistes, de forces de marée liées à l’étoile, ou de perturbations associées à des forces gravitationnelles dues à des objets supplémentaires dans le système (deuxième étoile, planète additionnelle, etc.). Elles se manifestent par des variations sur les timings des transits primaire et secondaire, soit sur le long terme, ce qui peut indiquer une précession de l’orbite, soit à plus court terme, dans le cas de perturbations par des planètes non nécessairement transitantes dans le système.
Les planètes sur des orbites résonantes, c’est-à-dire présentant des commensurabilités de leurs périodes – produisent des variations particulièrement grandes des instants des temps de transit (figure ci-jointe). Cette effet est appelé TTV (transit time variation). L’ « inversion » des données de TTV en termes de propriétés (masse et orbite) des planètes perturbatrices est souvent « dégénérée » (i.e. n’a pas de solution unique), mais dans certains cas, une solution non-ambigüe peut être obtenue. Le plus souvent, l’ordre de grandeur des TTV est une très faible fraction de la période orbitale.
Un cas remarquable est celui de l’exoplanète Kepler-88b, une planète de 9 masses terrestres, qui présente des TTV de 12h d’amplitude, pour une période orbitale de 11 jours. Il a été prédit qu’ils étaient causés par une planète perturbatrice non-transitante de 0.7 masses de Jupiter, qui est ensuite été détectée par vélocimétrie radiale !
Transit triple de planètes de TRAPPIST-1
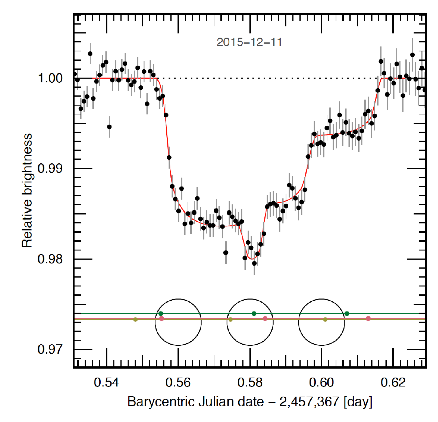
Courbe de lumière pour un transit triple des planètes TRAPPIST-1c, TRAPPIST-1e, et TRAPPIST-1f. La configuration des planètes (jaune, rouge, vert) à trois instants particuliers est indiquée en bas.
Crédit :
Gillon et al. 2017.
TRAPPIST-1 versus Jupiter
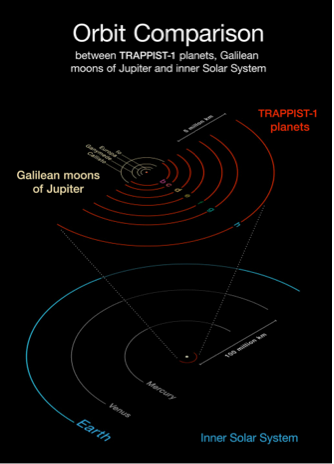
Taille comparée du système de 7 planètes TRAPPIST-1 avec le système des lunes galiléennes de Jupiter et le système solaire interne.
Crédit :
tréduire
Tout récemment (22 février 2017), un système exceptionnel de 7 planètes, toutes transitantes, a été découvert autour d’une étoile naine (rayon = 0.11 rayons solaires, masse= 0.08 masses solaires) ultra-froide (2550 K) appelée TRAPPIST-1 et située à 40 années-lumière. Les périodes orbitales (de 1.5 à 20 jours) sont telles que plusieurs de ces planètes peuvent transiter en même temps, et même s’occulter mutuellement pendant le transit, ce qui conduit à des courbes lumières d’une superbe complexité (Fig. ci-jointe).
Les tailles (Rp = 0.75 à 1.1 rayons terrestres) et masses (0.85 à 1.38 masses terrestres, mesurées par la méthode des TTV) indiquent clairement des planètes telluriques et trois d’entre elles pourraient avoir une température compatible avec l’eau liquide. Le système dans son ensemble (0.063 UA pour la planète la plus externe) tiendrait aisément dans l’orbite de Mercure, et apparaît comme un cas intermédiaire entre le système des satellites galiléens de Jupiter et celui du système solaire interne (Fig. ci-jointe).
Structure verticale - transit primaire
Dans ce qui précède, nous n’avons parlé de d’observations photométriques des transits – c’est-à-dire dans une seule bande de longueur d’onde (outre la description de l’effet Rossiter-McLaughlin). Par ailleurs, nous avons implicitement supposé que la planète a un « bord net », de sorte qu’on pouvait parler de son « rayon » sans ambiguÏté. La réalité est plus floue. Les planètes géantes n’ont pas de surface solide bien définie, et même une planète tellurique peut posséder une atmosphère, qui influence la manière dont la lumière stellaire est absorbée pendant le transit. Concrètement, l’absorption préférentielle de la lumière à certaines longueurs d’onde par les gaz et/ou aérosols/nuages rend le « rayon d’absorption » de la planète plus grand à ces longueurs d’onde. Du coup, la mesure spectroscopique du transit, c’est-à-dire la variation de la profondeur d’absorption du transit en fonction de la longueur d’onde, permet d’obtenir des informations sur la composition de l’atmosphère, voire sa dynamique. Nous verrons plus loin les équations générales régissant ces principes. Notons que cette spectroscopie de transmission peut être effectuée dans tout l’infrarouge et jusqu’à l’ultraviolet, ce qui permet en principe de sonder une vaste gamme verticale de niveaux dans l’atmosphère, allant des troposphères (pression de plusieurs bars) jusqu’aux thermosphères/exosphères (nanobar).
Structure verticale-transit secondaire
De même, il est extrêmement intéressant d’observer par spectroscopie l'éclipse secondaire. Comme on l’a vu, la différence entre le flux mesuré juste avant ou après le passage de la planète derrière l’étoile et celui mesuré pendant l'éclipse secondaire donne le rayonnement provenant de la planète elle-même (pour être précis, du côté éclairé de la planète). Selon le domaine de longueur d’onde, ce rayonnement planétaire peut-être de nature stellaire réfléchie ou thermique.
La première composante, qui domine dans le visible et le proche infrarouge, correspond à la lumière de l’étoile réfléchie par la planète. Le rayon étant approximativement connu par l’observation du transit, l’intensité de ce rayonnement réfléchi fournit l’albédo de la planète. Ce dernier résulte de la compétition entre les propriétés réfléchissantes/diffusantes et absorbantes de l’atmosphère (voire de sa surface). Pour une planète avec une atmosphère épaisse, les variations spectrales de l’albédo sont dues aux variations de ses propriétés de diffusion (par les gaz et/ou les nuages atmosphériques) avec la longueur d’onde, mais peuvent aussi faire intervenir la composition gazeuse (des espèces atomiques comme le sodium ou le potassium ont des raies d’absorption très fortes dans le visible). Comme on verra, la grande difficulté de la mise en œuvre de cette technique résulte dans la très faible intensité du signal planétaire à extraire.
Le domaine thermique, lui, correspond au rayonnement propre de l’atmosphère de la planète. Celui-ci dépend à la fois de la structure thermique verticale (la variation de la température avec la pression dans l’atmosphère de la planète) et des profils verticaux d’abondance des gaz – qui définissent le profil vertical de l’opacité atmosphérique. En termes de composition atmosphérique, la mesure du spectre thermique apparaît donc complémentaire de celle du spectre en transmission mesuré pendant le transit. Cette complémentarité reflète notamment le fait que les deux méthodes ne sondent pas les mêmes régions atmosphériques : le transit est sensible à la composition du limbe de la planète – i.e. les régions où la lumière stellaire est rasante (« terminateurs ») alors que l’émission thermique sonde le côté jour de la planète.
Par ailleurs, à une longueur d'onde donnée, le transit sonde des régions plus ténues de l'atmosphère que l'émission thermique.
Chimie de l'atmosphère
A ce jour (janvier 2017), la spectroscopie des transits a permis de détecter un petit nombre d’espèces chimiques dans certaines exoplanètes (~20 objets en tout), parmi lesquelles les molécules H2O, CO2, CO, CH4, et les espèces atomiques H, C, O, Na, K. De manière très générale, l’intérêt de ces mesures est double, permettant (i) d’en déduire la composition élémentaire (par exemple le rapport C/O), qui donne des contraintes sur les processus de formation de ces objets (ii) de caractériser les processus physiques (photochimie, condensation, thermochimie à l’équilibre ou hors-équilibre, transport vertical, échappement atmosphérique...) qui gouvernent les atmosphères. L’étude des spectres exoplanétaires renseigne aussi sur la présence de nuages dans leurs atmosphères, dans la mesure où des nuages diffusants ou absorbants à haute altitude masquent les absorptions moléculaires attendues.
Courbe de phase
Transits et courbe de phase de HD189733 b
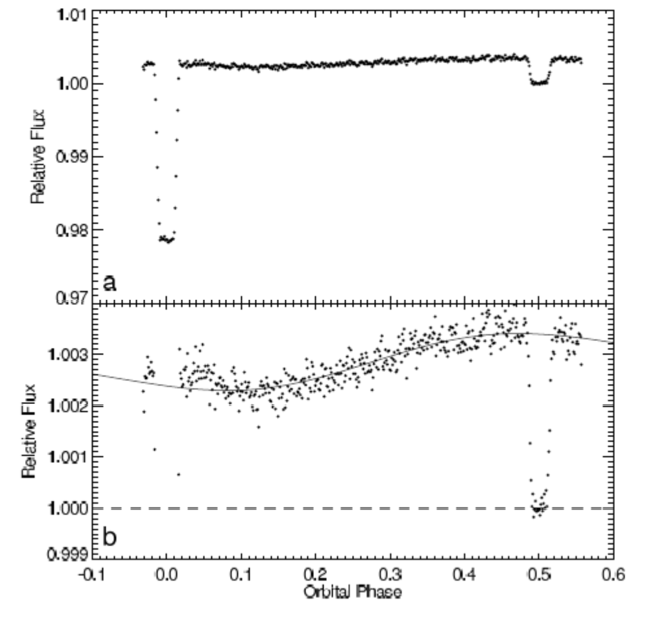
Figure 3 : Transit, éclipse secondaire, et courbe de phase de la planète HD 189733 b, observés à une longueur d’onde de 8
μm avec le télescope spatial infrarouge Spitzer. Les courbes sont normalisées au flux stellaire (1.000 pendant l'éclipse secondaire).
Le transit (à la phase 0.0) fait environ 2.1% de profondeur, ce qui indique un rapport des rayons
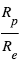
de 1.0%. L'éclipse secondaire (phase 0.5) indique que le côté jour de la planète émet 0.3% du rayonnement stellaire à cette longueur d’onde, impliquant une température d’environ 1210 K. La figure du bas (zoom vertical de celle du haut) montre la courbe de phase. Après modélisation, celle-ci indique que la température du côté nuit est d’environ 970 K, « seulement » 240 K plus froid que sur le côté jour, ce qui implique une forte redistribution de la chaleur par la dynamique atmosphérique. D’après Knutson et al. 2007.
Crédit :
à traduire
La figure montre qu’au cours de sa révolution autour de l’étoile, une exoplanète présente différentes phases : côté nuit au moment du transit, côté jour juste avant/après l'éclipse secondaire, et à l’instar de la Lune, des phases de croissant/quartier tout au long de l’orbite.
Le suivi de l’émission thermique avec la position de la planète sur son orbite – et ceci est vrai même pour une planète ne transitant pas – permet ainsi de mesurer les variations spatiales – en l’occurrence les variations avec l’heure locale pour une orbite circulaire – des propriétés atmosphériques. Ces courbes de phase renseignent principalement sur la variabilité diurne des températures atmosphériques. Par exemple, on pourrait s’attendre à ce que les Jupiter chauds, qui, dus aux effets de marée, sont en rotation synchrone autour de leur étoile, présentent des écarts de températures gigantesques entre les côtés éclairé et sombre. Ce n’est en fait souvent pas le cas (voir exemple sur la figure ci-jointe), ce qui implique une forte redistribution de la chaleur par des vents atmosphériques. Il est également généralement observé que le maximum de température ne se produit pas au midi local, mais est décalé vers les zones « de l’après-midi », ce qui s’explique par des effets d’inertie thermique.
Une méthode complémentaire consiste à résoudre temporellement l'éclipse secondaire dans le domaine thermique : la disparition progressive derrière l’étoile de la planète permet de déterminer successivement les températures de « tranches de planète » correspondant à des heures locales différentes, et ainsi d’établir une carte de températures.
La spectroscopie des transits donne enfin potentiellement un accès direct à la vitesse des vents atmosphériques. En effet si une molécule est détectée par spectroscopie du transit, la mesure précise de la longueur d’onde des raies planétaires peut éventuellement indiquer des décalages spectraux diagnostics de vitesses de vent. Ainsi, un décalage vers le bleu des raies de CO dans le cas de HD209458b a été interprété comme la signature de vents jour-nuit de l’ordre de 2 km/s. Des complications liées à la connaissance précise de l’orbite de la planète peuvent toutefois survenir. Dans un cas, il a aussi été possible de mesurer la période de rotation propre d’une exoplanète (β-Pictoris b) à partir de la largeur des raies de CO.

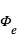 et celui de la planète
et celui de la planète 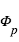 . Pendant l'éclipse secondaire, le flux mesuré est restreint à
. Pendant l'éclipse secondaire, le flux mesuré est restreint à 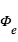 .
.
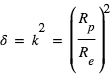 , où
, où 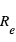 et
et 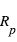 sont respectivement le rayon de l'étoile et de la planète. Le flux de lumière de l'étoile est réduit d'une fraction δ. Comme la planète est devant l’étoile, elle nous présente sa face non-éclairée, donc sa contribution au flux observé est nulle. En conséquence, le rapport du flux mesuré pendant le transit primaire à celui mesuré pendant l'éclipse secondaire (ou en pratique à celui mesuré à n’importe quel moment hors du transit) donne directement le rapport du rayon de la planète à celui de l’étoile.
sont respectivement le rayon de l'étoile et de la planète. Le flux de lumière de l'étoile est réduit d'une fraction δ. Comme la planète est devant l’étoile, elle nous présente sa face non-éclairée, donc sa contribution au flux observé est nulle. En conséquence, le rapport du flux mesuré pendant le transit primaire à celui mesuré pendant l'éclipse secondaire (ou en pratique à celui mesuré à n’importe quel moment hors du transit) donne directement le rapport du rayon de la planète à celui de l’étoile.
 Transit de planètes du système solaire
Transit de planètes du système solaire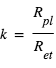 , mais également du rapport de l’intensité lumineuse spécifique (i.e. pour une surface donnée) émise par les deux objets. Comme on le verra plus loin, il dépend de de la longueur d’onde, et selon celle-ci, des températures de la planète et de l’étoile, ou de l’albédo de la planète.
, mais également du rapport de l’intensité lumineuse spécifique (i.e. pour une surface donnée) émise par les deux objets. Comme on le verra plus loin, il dépend de de la longueur d’onde, et selon celle-ci, des températures de la planète et de l’étoile, ou de l’albédo de la planète.
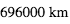 et Jupiter a un rayon de
et Jupiter a un rayon de 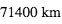 . La Terre a un rayon de
. La Terre a un rayon de 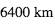 .
.






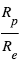 de 1.0%. L'éclipse secondaire (phase 0.5) indique que le côté jour de la planète émet 0.3% du rayonnement stellaire à cette longueur d’onde, impliquant une température d’environ 1210 K. La figure du bas (zoom vertical de celle du haut) montre la courbe de phase. Après modélisation, celle-ci indique que la température du côté nuit est d’environ 970 K, « seulement » 240 K plus froid que sur le côté jour, ce qui implique une forte redistribution de la chaleur par la dynamique atmosphérique. D’après Knutson et al. 2007.
de 1.0%. L'éclipse secondaire (phase 0.5) indique que le côté jour de la planète émet 0.3% du rayonnement stellaire à cette longueur d’onde, impliquant une température d’environ 1210 K. La figure du bas (zoom vertical de celle du haut) montre la courbe de phase. Après modélisation, celle-ci indique que la température du côté nuit est d’environ 970 K, « seulement » 240 K plus froid que sur le côté jour, ce qui implique une forte redistribution de la chaleur par la dynamique atmosphérique. D’après Knutson et al. 2007.