Comprendre
Auteur: JLB
- Plan
- Physique de la cible
- Introduction
- Mécanique
- Formation
- Disque zodiacal
- Corps Noir
- L'infrarouge Proche
- Age
- Source d'information
- Introduction
- Position
- Photométrie
- Magnitudes
- Acquérir l'information
- Introduction
- Optique ondulatoire
- Coronographie
- Coronographe, diffraction
- Coronographe, convolution
- Optique adaptative
- Tavelures
- Interferometrie
- Interférométrie annulante
- L'exemple de Darwin/TPF-I
- Imagerie différentielle
- Spectroscopie
- Restrictions sur la séparation observable
- Confirmation
- Deux époques
- Autres méthodes
- Le cas de Fomalhaut b
Plan
Physique de la cible
Auteur: JLB
Introduction
Fomalhaut b

Crédit :
ESA/NASA
Commençons par étudier ce qui se passe d'un point de vue physique dans le système planétaire que l'on va chercher à imager:
Mécanique
La planètes suivent les lois de la mécanique découvertes par Newton. En particulier, elles sont soumises à la force de gravitation universelle qui définit des orbites képlériennes.
La position et le mouvement relatif de la planète par rapport à son
étoile vont nous permettre de contraindre les éléments de l'orbite (demi
grand axe, inclinaison, excentricité), sa période et donc les masses des
corps.
Éléments d'une orbite
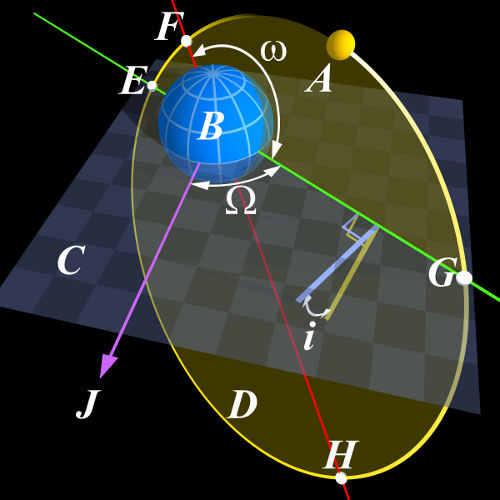
A – planète
B – étoile
C – plan de référence, l'écliptique
D – Plan orbital de la planète
E – noeud descendant
F – Périapse
G – noeud ascendant
H – Apoapse
i – Inclinaison
J – Direction de référence (ligne de visée)
Ω – Longitude du noeud ascendant
ω – Argument du périapse
Pour aller plus loin.
Formation
Une planète commence sa formation sous la forme d'un noyau solide qui grossit par accrétion de matière.
Si la masse de ce planétoïde dépasse quelques dizaines de 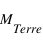 (1
(1 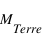 correspondant à une fois la masse Terre) , l'accrétion de gaz augmente brutalement pour former une planète géante.
correspondant à une fois la masse Terre) , l'accrétion de gaz augmente brutalement pour former une planète géante.
Naissance d'une planète géante
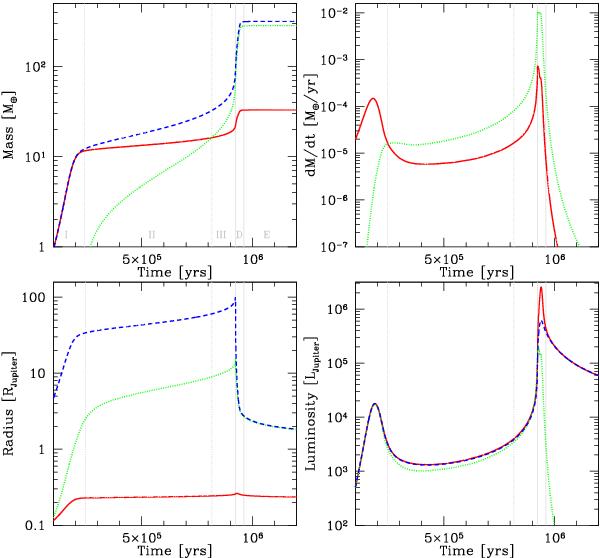
En 2012, Christoph Mordasini et collaborateurs publient dans Astronomy and Astrophysics une étude sur la formation des planètes, ici celle de Jupiter, de haut en bas et de gauche à droite, se trouvent l'évolution de la masse, du taux d'accrétion, du rayon et la luminosité de la planète en fonction du temps.
Remarque: Instabilités gravitationnelles
Le modèle précédent, dit de "core accretion" ou accrétion de coeur, n'est pas le seul existant pour expliquer la formation des planètes géantes, un autre modèle est basé sur les modèles de formation des étoiles. En effet les instabilités gravitationnelles dans le disque protoplanétaire provoquent une fragmentation de celui-ci suivi d'effondrements locaux menant à la formation directe d'astres principalement gazeux... Identifier le mode de formation est donc une tache complexe, et l'imagerie directe donne des pistes pour ce faire (notamment la luminosité ou la température en fonction de l'âge de la planète mais aussi sa position par rapport à l'étoile).
Pour en savoir plus, reportez-vous au cours sur la formation des planètes en cliquant ici.
Disque zodiacal
Lorsqu'une étoile vient de se former, elle est entourée d'un disque de poussière et de gaz comme β Pictoris par exemple RAJOUTER LE LIEN. C'est dans ce dernier que vont se former les planètes.
Au fil de l'évolution du système planétaire, ce disque va être alimenté par les collisions entre les comètes et les astéroïdes. Ce disque de poussière est très lumineux dans les systèmes jeunes. Il absorbe le rayonnement de l'étoile et son émission (principalement dans l'infrarouge lointain) va avoir tendance à gêner l'observation directe des exoplanètes.
Dans le système solaire le contraste moyen entre la lumière zodiacale et la lumière solaire est de 7 ordres de grandeur.
alors que le rapport des masses entre le disque de poussière et les planètes vaut 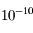 et que le disque s'étend de 5 à plusieurs centaines d'UA.
Il existe des étoiles autour desquelles on trouve un disque plus de 1200 fois plus brillant, comme η Corvi !
et que le disque s'étend de 5 à plusieurs centaines d'UA.
Il existe des étoiles autour desquelles on trouve un disque plus de 1200 fois plus brillant, comme η Corvi !
On exprime l'intensité diffusée par la poussière interplanétaire en zodi, 1 zodi étant l'intensité diffusée par le disque de notre système solaire.
Disque

Image composite combinant le disque et la planète en orbite autour de β pictoris (ici masquée, au centre du cercle) .
Corps Noir
Tout corps, à une température donnée, émet un rayonnement particulier appelé rayonnement thermique (ou par abus, rayonnement de corps noir, un corps noir étant un corps parfaitement absorbant à toutes les longueurs d'onde).
Le spectre du rayonnement d'un corps noir ne dépend que de sa température 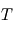 . La longueur d'onde
. La longueur d'onde 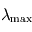 où ce spectre atteint son maximum est donnée par la loi de Wien:
où ce spectre atteint son maximum est donnée par la loi de Wien: 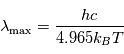 .
. 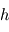 ,
, 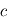 et
et 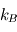 désignent respectivement les constantes de Planck, la vitesse de la lumière et la constante de Boltzmann. Un corps chaud présente donc un pic d'émission décalé vers les courtes longueurs d'onde par rapport à un corps plus froid. Aux températures ambiantes, ce pic est dans l'infrarouge (dit infrarouge thermique), mais pour des corps atteignant une température plusieurs milliers de Kelvins, ce maximum se décale dans le spectre visible : c'est le cas des étoiles par exemple, ou bien d'un tison chauffé à blanc.
désignent respectivement les constantes de Planck, la vitesse de la lumière et la constante de Boltzmann. Un corps chaud présente donc un pic d'émission décalé vers les courtes longueurs d'onde par rapport à un corps plus froid. Aux températures ambiantes, ce pic est dans l'infrarouge (dit infrarouge thermique), mais pour des corps atteignant une température plusieurs milliers de Kelvins, ce maximum se décale dans le spectre visible : c'est le cas des étoiles par exemple, ou bien d'un tison chauffé à blanc.
Le flux total 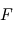 (intégré sur toutes les longueurs d'onde) émis par un corps noir ne dépend également que de sa température, suivant la loi de Stefan-Boltzmann :
(intégré sur toutes les longueurs d'onde) émis par un corps noir ne dépend également que de sa température, suivant la loi de Stefan-Boltzmann : 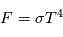 où
où 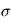 désigne la constante de Stefan-Boltzmann. Un corps chaud rayonne donc bien davantage qu'un corps froid.
désigne la constante de Stefan-Boltzmann. Un corps chaud rayonne donc bien davantage qu'un corps froid.
La température du corps noir émettant autant de flux thermique que la planète est appelée température efficace (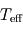 ) de la planète. Elle est en règle générale voisine de la température physique de la région de la planète d'où est principalement issue l'émission thermique (atmosphère, voire surface solide pour des planètes telluriques dotées d'une atmosphère mince).
) de la planète. Elle est en règle générale voisine de la température physique de la région de la planète d'où est principalement issue l'émission thermique (atmosphère, voire surface solide pour des planètes telluriques dotées d'une atmosphère mince).
Or, on a pu voir précédemment, que le processus de formation des planètes était un processus impliquant des chocs et autres phénomènes violents, ce qui provoque un dégagement d'énergie considérable sous forme de chaleur.
Evolution température
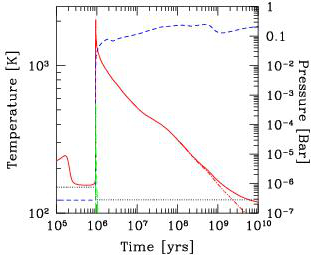
En 2012, Christoph Mordasini et collaborateurs publient dans Astronomy & Astrophysics une étude sur la formation des planètes, ici celle de Jupiter. En rouge vous pouvez remarquer l'évolution de la température efficace de la planète en fonction du temps.
Vous pouvez remarquer que, une fois formée, plus la planète est jeune, plus elle est chaude, et donc plus important est le flux lumineux qu'elle émet. Mais aussi plus la longueur d'onde du maximum de luminosité est courte (et se rapproche du domaine visible) ! Ainsi Jupiter émet actuellement son maximum d'émission autour de 30 µm, tandis que β Pictoris b l'émet autour de 1,7 µm.
Pour en savoir plus.
L'infrarouge Proche
Le rayonnement de corps noir des jeunes exoplanètes géantes culmine généralement dans le proche infrarouge. C'est une chance car il y a de nombreuses raies moléculaires (méthane, monoxyde de carbone...) et atomiques (Na, K ...) dans ce domaine spectral, ce qui permet potentiellement d'analyser la composition chimique de ces planètes.
Pour observer depuis le sol dans ce domaine de longueurs d'onde, il faut hélas se restreindre aux fenêtres de transparence de l'atmosphère terrestre, comme les fenêtres J,H et K situées dans le proche infrarouge (voir l'image ci-dessous).
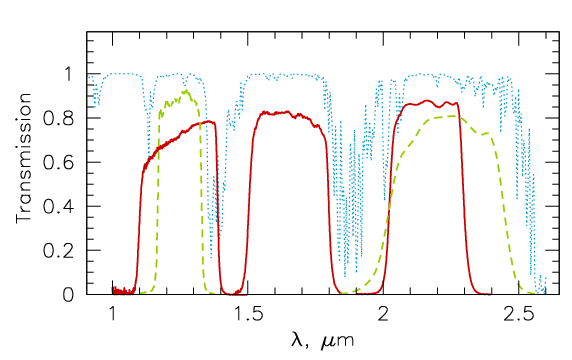
Filtres J (∼1,1-1,4 μm), H(∼1,5-1,8 μm) et (∼2-2,5 μm)K (en rouge et vert) disponible dans le proche infrarouge à l'ESO, comparé à la transmission de l'atmosphère terrestre (bleu).
Age
La formation des planètes étant quasi-concomittante à celle de leur étoile hôte, on assimile souvent l'âge de la planète à celui de son étoile. Par exemple la Terre a terminé sa formation 20 millions d'années après le Soleil, ce qui est négligeable en comparaison des 4,6 milliards d'années du système solaire.
Fragmentation d'un nuage interstellaire
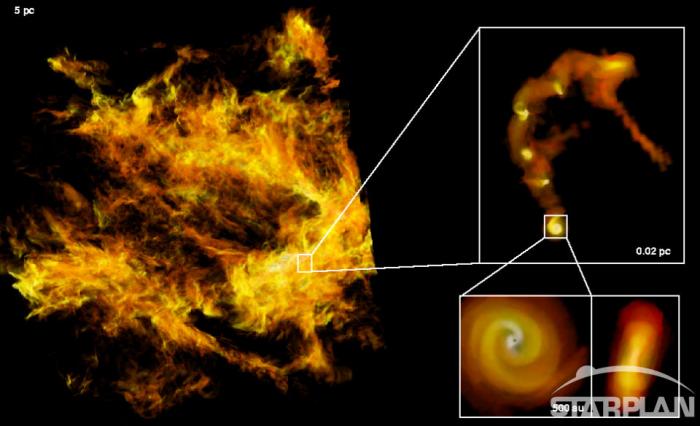
Modèle de formation de disque protoplanétaire par fragmentations d'un nuage se situant dans le milieu interstellaire. Dans ce nuage un très grand nombre d'étoiles sont en formation en même temps, mais elles sont de masses différentes. Nous allons pouvoir répartir les étoiles résultantes sur un diagramme HR et, suivant leur emplacement, pouvoir dater le groupe d'étoiles et donc contraindre l'âge des exoplanètes possiblement présentes.
Groupe local
Pour déterminer l'âge d'une étoile on peut déterminer, par son mouvement propre, à quel groupe d'étoiles elle appartient. Le groupe d'étoiles, dont les étoiles ont été formées au même moment et se déplaçant dans la même direction, peut nous donner son âge grâce à sa répartition au sein du diagramme HR.
http://astro.unl.edu/naap/hr/animations/hr.html
Activité
Age/Activité
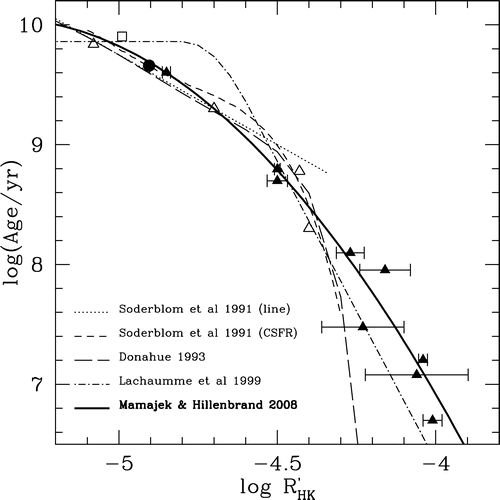
Eric E. Mamajek et Lynne A. Hillenbrand ont publié en 2008 dans
the Astrophysical Journal une étude sur les estimateurs d'âge des étoiles de type solaire. Ce graphique nous présente la répartition des âges, en ordonnées (en années et en échelle logarithmique), en fonction d'un marqueur d'activité à savoir
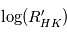
: plus il est élevé, plus l'activité est grande. Les courbes représentes plusieurs tentatives pour déterminer une relation entre ces deux observables.
On peut aussi relier, pour un type stellaire donné, l'âge à l'activité et à la couleur de l'étoile. La couleur s'obtient en prenant deux mesures de flux photométriques dans deux domaines de longueur d'onde différents. Pour l'activité, l'observation de plusieurs marqueurs spectroscopiques est possible ainsi que l'émission dans le domaine des rayons X.
Activité/X
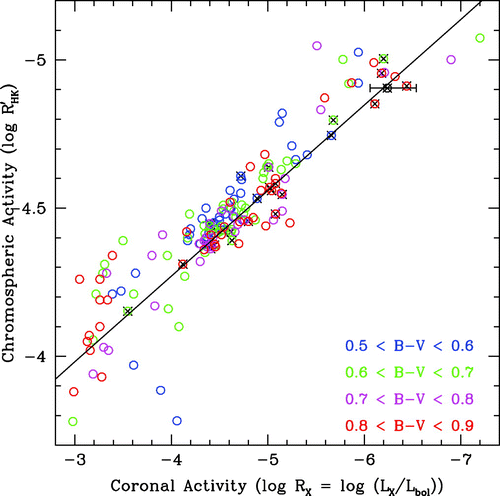
Dans le même article de Eric E. Mamajek et Lynne A. Hillenbrand, on trouve ce graphique qui nous présente une relation linéaire entre le marqueur spectroscopique qu'est le
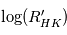
et le rayonnement en X .
B-V est l'indice de couleur des étoiles qui peut donc être relié à leur type spectral.
Rotation
La rotation de l'étoile est aussi liée à l'activité et donc à son âge, la comparaison de la rotation propre d'une étoile avec sa couleur va donc nous permettre de remonter à ce premier paramètre, pour un type spectral donné.
Rotation/Activité
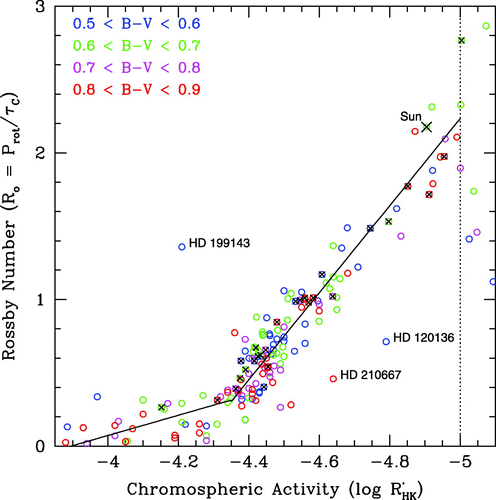
L'article de Eric E. Mamajek et Lynne A. Hillenbrand présente enfin ce graphique qui nous présente les relations linéaires entre le marqueur spectroscopique qu'est le
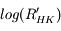
et la rotation de l'étoile exprimée par le
nombre de Rossby.
Source d'information
Auteur: JLB
Introduction
Les planètes et les étoiles émettent des photons dans l'espace et certains vont arriver jusqu'à la Terre... Notre seule source d'information, ce sont ces photons !
Les observations sont effectuées avec un ou plusieurs télescopes, qui vont collecter et envoyer un grand nombre de photons au foyer de l'instrument. L'image se forme alors sur un capteur CCD (Charge-Coupled Device, dispositif à transfert de charges), qui est un récepteur à photons transformant ces derniers par effet photoélectrique en courant électrique. Ceci permet donc l'enregistrement d'une image notamment pour être envoyée et traitée par un ordinateur.
Sont identifiables sur l'image obtenue par le capteur CCD :
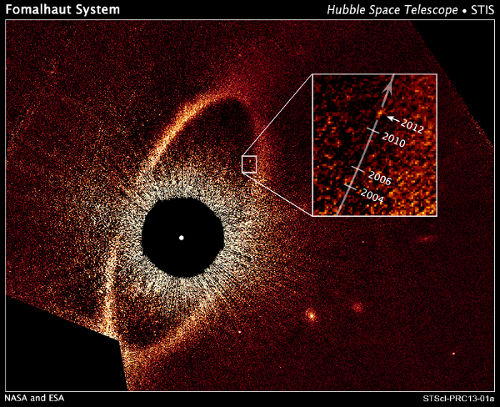
Observation de Fomalhaut b
Position
Photométrie
La lumière qui nous permet d'identifier la planète provient de plusieurs mécanismes physiques.
L'étoile émet de la lumière au niveau de sa photosphère, dont l'intensité et la couleur vont dépendre de sa température efficace (cf. corps noir).
Mais la planète (suivant son éloignement par rapport à son étoile) va réfléchir une partie de la lumière stellaire suivant son albédo (littéralement sa capacité à réfléchir la lumière). Elle va aussi émettre sa propre émission thermique selon sa propre température efficace. AJOUTER LIEN.
On exprime la différence d'intensité lumineuse 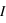 entre l'étoile et la planète grâce au contraste, définit comme :
entre l'étoile et la planète grâce au contraste, définit comme :
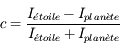
Le contraste en magnitude est défini comme la différence de magnitude (LIEN VERS PAGE SUIVANTE) entre la planète et l'étoile.
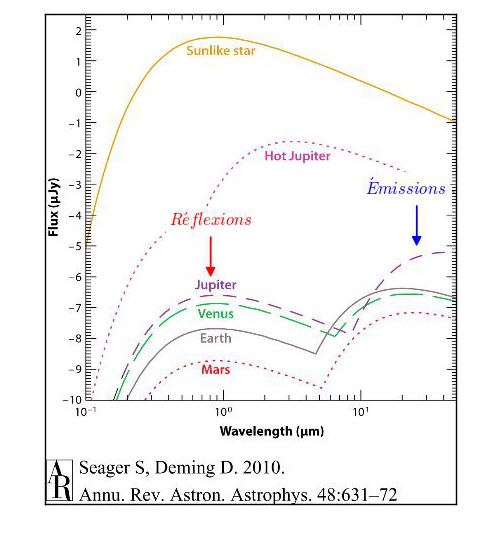
Comme nous l'avons vu précédemment, le flux lumineux émis par les planètes du système solaire se compose de deux parties, une partie (au niveau de la flèche rouge) dû à l'albédo de la planète qui va provoquer une réflexion de la lumière solaire (avec un maximum au même endroit que le maximum solaire, puisqu'il s'agit de la même lumière) et une partie d'émission thermique propre (au niveau de la flèche bleue). La température des planètes étant plus froide que celle de leur étoile, ce second maximum local se situe à de plus grandes longueurs d'onde.
Pour aller plus loin sur la photométrie, cliquer ici.
Magnitudes
Pour mesurer la luminosité d'un objet en astrophysique, on utilise les magnitudes.
Par définition la magnitude 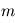 est liée au flux spectral émis ou réfléchi
est liée au flux spectral émis ou réfléchi 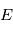 par la formule
par la formule 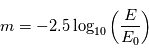 où
où 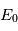 est le flux spectral d'une étoile de référence (par défaut Véga) qui correspond arbitrairement à une magnitude de 0.
est le flux spectral d'une étoile de référence (par défaut Véga) qui correspond arbitrairement à une magnitude de 0.
En général on considère deux types de magnitudes :
- la magnitude apparente qui correspond à la luminosité observée, notée
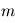 (minuscule) avec indication optionnelle d'une bande spectrale (ainsi un objet observé dans un filtre V, correspondant à la bande "visible" autour de 551 nm, verra sa magnitude apparente notée
(minuscule) avec indication optionnelle d'une bande spectrale (ainsi un objet observé dans un filtre V, correspondant à la bande "visible" autour de 551 nm, verra sa magnitude apparente notée 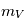 ou même
ou même 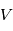 )
) - la magnitude absolue qui correspond à la luminosité apparente de l'objet s'il était placé à 10 pc de nous, notée
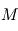 (majuscule) :
(majuscule) : 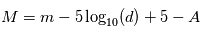 avec
avec 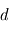 la distance séparant l'observateur de l'objet en parsec et
la distance séparant l'observateur de l'objet en parsec et 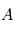 un facteur de correction provenant de l'absorption par le milieu interstellaire, négligeable sur les courtes distances. Si on consiodère la même bande spectrale que dans l'exemple précédent, la magnitude absolue sera notée
un facteur de correction provenant de l'absorption par le milieu interstellaire, négligeable sur les courtes distances. Si on consiodère la même bande spectrale que dans l'exemple précédent, la magnitude absolue sera notée 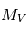 .
.
[Pour aller plus loin.]
Les magnitudes sont d'usage courant en astronomie et très utiles. Elles permettent, entre autres choses, de construire des diagrammes couleur-magnitude ou couleur-couleur qui donnent des informations similaires au diagramme HR tout en pouvant être construits beaucoup plus facilement à partir des observations disponibles. Ici, une couleur désigne la différence entre deux magnitudes observées dans deux bandes spectrales différentes.
Diagramme couleur-couleur
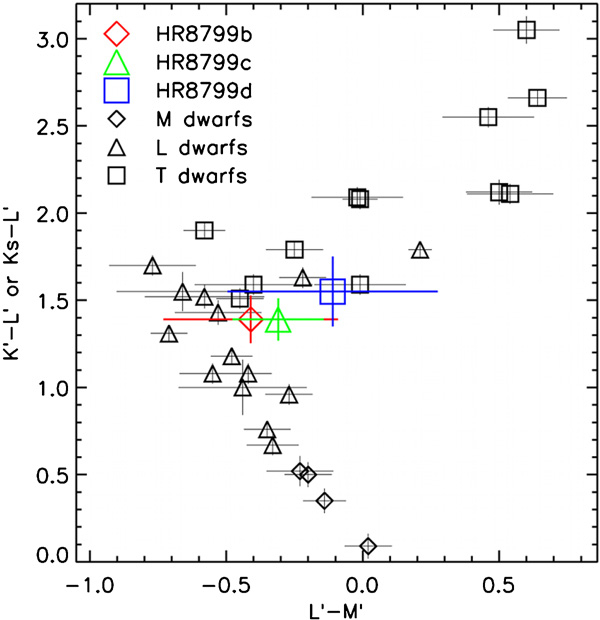
Diagramme couleur-couleur comparant les naines rouges (M dwarfs) naines brunes (L et T dwarfs) et les planètes HR8799 b,d et d.
Ici on compare des observations dans l'infrarouge dans avec des filtres K',Ks,L' et M'..
[Pour aller plus loin.]
Acquérir l'information
Auteur: JLB
Introduction

De gauche à droite : image de l’étoile corrigée par optique adaptative, image de l’étoile atténuée par coronographie, SDI, ADI (ces sigles recouvrent des techniques expliquées par la suite).
Une fois les photons observés, il faut trouver puis étudier les éventuelles planètes... Or ce n'est pas chose facile : les planètes ne sont pas du tout visibles directement dans les données brutes (les deux premières images en partant de la gauche de la figure ci-dessus).
Il faudra donc utiliser certains concepts avancés de traitement du signal :
Hubble space telescope

Crédit :
NASA
Optique ondulatoire
La lumière est une onde électromagnétique, et l'intensité lumineuse est proportionnelle au carré de l'amplitude de cette onde. Comme toute onde, elle est sujette aux phénomènes de diffraction et d'interférence, qui vont être particulièrement importants ici. Ainsi l'image de l'étoile hôte, que l'on assimile a une source ponctuelle vue depuis la Terre, va devenir une tache d'Airy (voir image ci-dessous) sur le récepteur du fait de l'utilisation d'instruments d'ouverture finie (l'ouverture est directement reliée au diamètre du miroir principal du télescope). La lumière de l'étoile va donc s'étaler sur l'ensemble du détecteur, compliquant la détection de la ou des planètes éventuellement présentes !
Il est important de remarquer que cette tache centrale a une taille caractéristique proportionnelle à la longueur d'onde et inversement proportionnelle à l'ouverture du télescope. Cela implique que pour avoir une résolution suffisante, il faut une ouverture en adéquation avec la longueur d'onde : pour pouvoir espérer observer une planète proche de son étoile dans l’infrarouge lointain, il faudrait ainsi un télescope de plusieurs dizaines de mètres d'ouverture !

Image simulée d'une source ponctuelle à travers un instrument d'ouverture finie et circulaire : tache d'Airy
Mais cet aspect ondulatoire présente aussi des avantages : il permet de mettre en œuvre des techniques d'observation basées sur la combinaison de plusieurs télescopes. Ainsi, l'interférométrie permet ainsi de combiner plusieurs télescopes individuels et distants les uns des autres pour obtenir un gain de séparation angulaire. L'interférométrie permet aussi d'occulter l'étoile hôte en jouant sur les interférences destructives.
[Pour aller plus loin]
Coronographie
Comme constaté précédemment, l'image de l'étoile hôte formée sur le récepteur d'un instrument se présente sous la forme d'une tache qui recouvre les images des planètes tournant éventuellement autour d'elle. Notre but va donc être de retirer l'image de l'étoile et d'autres résidus parasites qui pourraient se former à cause des phénomènes de diffraction et d'interférence (les tavelures). Un moyen naturel de retirer la lumière d'une étoile, observable sur Terre depuis l'aube des temps, est le phénomène de l'éclipse solaire, où le Soleil est masqué par la Lune.
Coronographe de Lyot
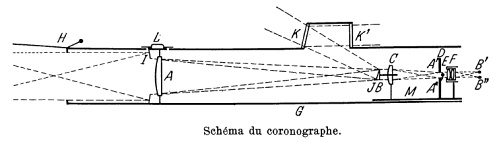
Schéma original du coronographe de Lyot, tel qu'il le présenta lui-même en 1932. La lentille placée en A forme l'image du soleil sur un disque en B, légerement moins large que l'image du soleil. Puis la lentille C produit une image A'A" sur un diaphragme dont le centre est occupé par le petit écran E. Les bords du diaphragme arrêtent la lumière diffractée par les bords de la première lentille, le petit écran arrête la lumière des images solaires produites par les réflexions parasites sur les faces de la lentille. L'image de la seule couronne solaire finit par apparaître en B'B".
C'est sur ce principe que l'astrophysicien Bernard Lyot développa au début du vingtième siècle un coronographe, instrument qui permet de cacher la lumière du soleil par l'utilisation d'un masque
disposé sur le chemin optique et d'un collimateur pour atténuer les résidus.
Les instruments qui font de l'observation en imagerie directe d'exoplanète utilisent ce même concept, voire des versions plus évoluées : coronographie de phase, coronographie interférentielle achromatique, etc.
[Pour en savoir plus sur les coronographes actuels et futurs cliquez ici.]
Coronographe, diffraction
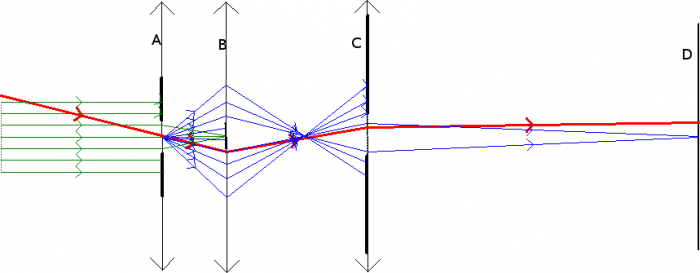
Représentation du fonctionnement d'un coronographe de Lyot.
Crédit :
JLB pour SESEP
Voici ce qui se passe dans un coronographe de Lyot, expliqué au moyen de l'optique géométrique. La lumière de l'étoile (vert) et celle de la planète (rouge), sont légerement décalées d'un certain angle sur le ciel. Si l'on place la lumière de l'étoile dans l'axe de l'instrument, celle de la planète arrive avec un certain angle, on dit que la planète est située hors-axe. Une lentille placée en A va donc faire converger en son foyer image les rayons de l'étoile mais pas ceux de la planète, il suffit alors de placer un petit écran au foyer image (dans le plan B) de la lentille (placée en A) pour arrêter toute la lumière provenant de l'étoile et ne garder que celle de la planète, dont on forme finalement l'image seule sur l'écran D.
Malheureusement cela ne fonctionne pas directement. En effet, il faut considérer ici le fait que l'ouverture de l'instrument est finie (le télescope a un certain diamètre), ce que l'on modélise ici par la présence d'un collimateur en A.

Dans le cadre de l'optique ondulatoire, si une onde plane passe à travers un trou, elle change de forme, le trou devient virtuellement l'emplacement d'une nouvelle source de lumière : c'est le phénomène de diffraction. Le principe de de Huygens présente qu'en optique ondulatoire,
chaque point atteint par l'onde se comporte comme une nouvelle source
ponctuelle)
En tenant compte du phénomène de diffraction par l'entrée de l'instrument (rayons en bleu), une partie importante des rayons difractés ne sont pas arrétés par l'écran en B. Il faut donc placer un autre diaphragme sur le chemin, en C, qui va bloquer la plus grande partie des rayons diffractés.
Dans une approche pleinement ondulatoire (on utilisera le formalisme complexe par la suite) : si l'on considère l'amplitude 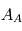 de l'étoile avant l'entrée dans l'instrument de diamètre
de l'étoile avant l'entrée dans l'instrument de diamètre 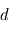 et sa phase
et sa phase 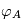 , alors la phase du rayon provenant de la position
, alors la phase du rayon provenant de la position 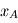 sur le plan A, vu à la position angulaire
sur le plan A, vu à la position angulaire 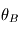 au niveau du plan B est donnée par
au niveau du plan B est donnée par 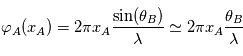 dans l'approximations de Gauss (petits angles hors-axe).
dans l'approximations de Gauss (petits angles hors-axe).
L'amplitude reçue au niveau du plan B depuis tous les points source virtuels dans l'ouverture en A est alors donnée par intégration : 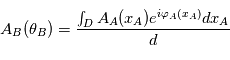 ou, en omettant le facteur de normalisation :
ou, en omettant le facteur de normalisation : 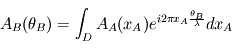 . L'amplitude de lumière reçue dans l'instrument, venant de l'étoile, est donc dépendante du diamètre
. L'amplitude de lumière reçue dans l'instrument, venant de l'étoile, est donc dépendante du diamètre 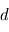 de l'instrument et de la longueur d'onde d'observation
de l'instrument et de la longueur d'onde d'observation 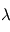 .
.
Coronographe, convolution
Coronographie, effets

Image de l'étoile, étape par étape, sur le trajet optique du coronographe.
Crédit :
LESIA
En fait, à chaque étape, les images intermédiaires vont être convoluées (voir ici, partie Transformée de Fourier et de Laplace, là et là) par la fonction de transmission de l'instrument (masque, diaphragmme ...) et va voir son intensité diminuer.
Au niveau du plan C (indiqué par stop dans le schéma ci-dessus), après le passage du masque (mask), on obtient une amplitude de formule :  où
où 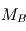 est la fonction de transmission du masque placé en B. Dans le cadre d'un coronographe,
est la fonction de transmission du masque placé en B. Dans le cadre d'un coronographe, 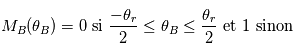 . L'amplitude au niveau du plan C va être donc être atténuée par rapport à celle au niveau du plan B, ce rapport dépendant de celui entre la taille angulaire du masque
. L'amplitude au niveau du plan C va être donc être atténuée par rapport à celle au niveau du plan B, ce rapport dépendant de celui entre la taille angulaire du masque 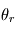 et l'ouverture
et l'ouverture 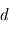 de l'instrument.
de l'instrument.
Au niveau où l'on place le détecteur, en D, l'amplitude finalement observée est donnée par : 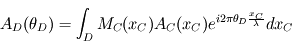 où
où 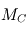 est la fonction du transmission du Lyot-Stop, un diaphragme dont on considérera la fonction de tranmission également rectangulaire :
est la fonction du transmission du Lyot-Stop, un diaphragme dont on considérera la fonction de tranmission également rectangulaire : 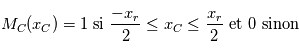 .
.
On montre alors que l'amplitude de la lumière entrant dans l'axe de l'instrument (celle de l'étoile) va diminuer selon le rapport 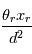 : plus le masque sera grand et le Lyot-Stop fermé, plus la lumière de l'étoile sera "éteinte" et donc plus facilement la planète sera visible. Attention toutefois, la lumière provenant d'une éventuelle planète doit quant à elle être transmise ! Il faut donc trouver un compromis entre la diminution d'intensité de la lumière de l'étoile et la conservation de l'intensité en provenance d'une éventuelle planète, dont on ne connaît pas a priori la séparation angulaire avec l'étoile...
: plus le masque sera grand et le Lyot-Stop fermé, plus la lumière de l'étoile sera "éteinte" et donc plus facilement la planète sera visible. Attention toutefois, la lumière provenant d'une éventuelle planète doit quant à elle être transmise ! Il faut donc trouver un compromis entre la diminution d'intensité de la lumière de l'étoile et la conservation de l'intensité en provenance d'une éventuelle planète, dont on ne connaît pas a priori la séparation angulaire avec l'étoile...
Optique adaptative
Nous venons de voir que la coronographie permet de retirer la majorité de la lumière provenant de l'étoile... mais d'une étoile théorique, considérée comme ponctuelle ! Or il n'y a pas que les effets d'optique ondulatoire au sein de l'instrument qui entrent en jeu, mais aussi (dans le cas des instruments au sol) les effets de l'atmosphère terrestre. À elle seule cette dernière va modifier la forme de l'image de l'étoile, ce qui va accentuer les résidus et ce d'une façon très variable dans le temps, du fait notamment du vent. Ces effets atmosphériques se manifestent par la déformation des fronts d'onde, et dégradent la résolution angulaire de l'instrument au-delà des limites théoriques imposées par l'optique ondulatoire (dépendant de l'ouverture et de la longueur d'onde). Dans les cas les plus extrêmes, ces déformations optiques sont mêmes visibles à l'oeil nu : c'est le fourmillement apparent d'un objet observé au-dessus d'une route asphaltée en été, ou au-dessus d'un barbecue...
Correction

À gauche, une observation sans optique adaptative. À droite la même cible avec optique adaptative, qui nous révèle que l'objet est une en fait une étoile binaire.
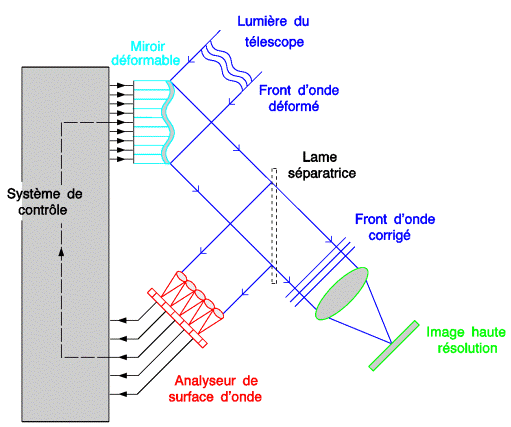
Pour s'opposer à ces effets, on utilise l'optique adaptative. Cette technique analyse le front d'onde après réflexion sur un miroir déformable, puis modifie la forme du miroir pour compenser les effets de l'atmosphère en temps réel.
Fonctionnement
Tavelures
Dans les précédentes parties nous avons vu les techniques utilisées pour retirer la lumière de l'étoile hôte et corriger les perturbations sur le chemin de la lumière... mais ces corrections ne sont pas parfaites !
Sur le détecteur, nous voyons des taches dispersées qui sont les résidus que la coronographie et l'optique adaptative n'ont pas réussi à corriger. Le problème est que ces taches peuvent être prises pour des planètes ou se superposer aux images de ces dernières. Nous allons donc devoir tenter de retirer ces résidus, aussi appelés artefacts.
Exemple de tavelures
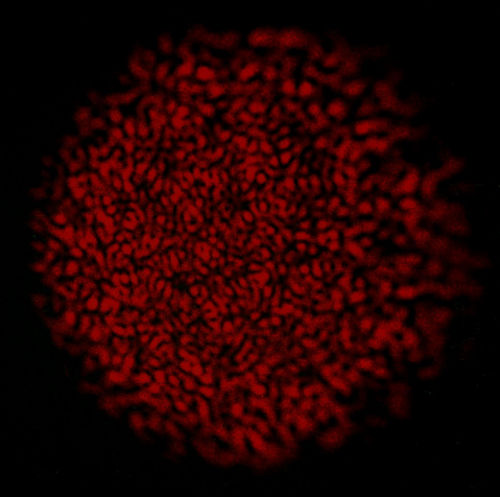
Image produite par un faisceau laser après passage dans une fibre optique. On voit des tavelures, les mêmes que l'on pourrait observer. Les causes possibles sont multiples : des fibres optiques (comme ici), mais aussi la turbulence atmosphérique imparfaitement corrigée, les imperfections des miroirs, etc.
Interferometrie
Présentation
Une manière différente d'aborder le problème est de passer par l'interférométrie, et en particulier l'interférométrie annulante. L'idée de base va être d'utiliser au moins deux télescopes assez éloignés pour augmenter la résolution angulaire (et donc bien distinguer l'étoile de l'éventuelle planète), et d'essayer de diminuer l'intensité en provenance de l'étoile (mais pas de la planète !) au moyen d'interférences destructives.
Interférométrie annulante
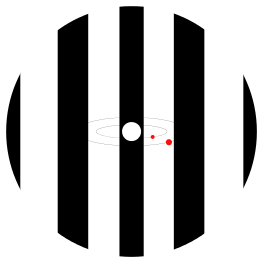
Représentation d'une observation par interférométrie annulante. Le disque blanc au centre est placé à l'endroit où se trouve l'étoile, qui se retrouve complètement masquée par les interférences (destructives : bandes noires) alors que les planètes en rouge ne sont pas masquées.
Intérêt
Nous avons parlé précédemment de la coronographie qui est utilisée sur des grands télescopes, notamment ceux de 8 m de diamètre du VLT. Ces instruments travaillent dans le proche infrarouge et le visible mais ne peuvent pas atteindre de plus grandes longueurs d'onde comme l'infrarouge moyen qui serait pourtant très intéressant pour étudier les raies spectrales des molécules, ou pour étudier des planètes plus froides émettant leur spectre thermique à de plus grandes longueurs d'onde. Le problème vient du fait qu'un télescope de 8 m de diamètre ne peut pas facilement séparer les sources à grandes longueurs d'onde, le pouvoir de résolution d'un télescope étant proportionnel à 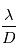 . Il faut donc augmenter la taille du télescope, ou combiner le flux de plusieurs télescopes comme nous le présentons ici. On peut alors aisément obtenir une ligne de base de 100 m en séparant 2 télescopes de cette distance.
. Il faut donc augmenter la taille du télescope, ou combiner le flux de plusieurs télescopes comme nous le présentons ici. On peut alors aisément obtenir une ligne de base de 100 m en séparant 2 télescopes de cette distance.
Interférométrie annulante
Plusieurs étapes-clés sont à mettre en oeuvre pour l'interférométrie annulante :
Chaque téléscope collecte une partie du même front d'onde en provenance du système exoplanétaire.
On relie les télescopes entre eux par fibres optiques, et on ajuste les chemins optiques dans chaque fibre pour égaliser les phases.
On déphase ensuite au moins l'un des chemins optiques par rapport aux autres (déphasage de 180° dans le cas d'un système à deux télescopes).
On combine alors tous les flux sur le même détecteur.
Ce système annule alors la lumière située sur l'axe optique (celle de l'étoile) par interférences destructives mais pas la lumière hors axe (celle des planètes). Le déphasage en entrée de l'instrument sera donné par 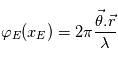 où
où 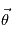 désigne l'écart sur le ciel entre la planète et l'étoile (donc dans une direction normale à l'axe optique), et
désigne l'écart sur le ciel entre la planète et l'étoile (donc dans une direction normale à l'axe optique), et 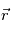 est la séparation entre la planète et l'étoile dans la direction de l'axe optique.
est la séparation entre la planète et l'étoile dans la direction de l'axe optique.
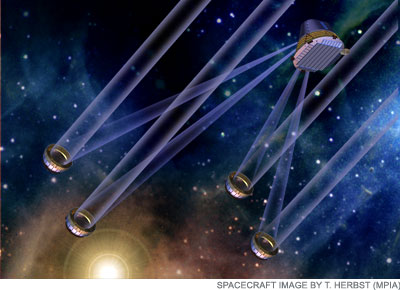
L'exemple de Darwin/TPF-I
Deux satellites de recherche d'exoplanètes par interférométrie font partie des projets à long terme des agences spatiales européenne et américaine, ce sont respectivement les missions Darwin et TPF-I. Difficiles à mettre en oeuvre techniquement, ces missions nécessitent encore des développements technologiques pour envisager leur réalisation.
Comme vous pouvez le voir sur l'illustration ci-dessus, l'idée et de faire voler en formation 4 quatres satellites "miroirs", combinant leurs faisceaux sur un cinquième satellite, la longue ligne de base étant négligeble devant la "distance focale" de l'instrument (le dernier satellite est très éloigné des 4 premiers). Pour être efficace, chaque faisceau va recevoir un déphasage précis selon deux configurations (appelées droite et gauche).
| Configuration | 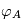 | 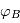 | 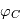 | 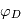 | Signal attendu |
|---|
| Gauche | 0° | 180° | 90° | 270° | étoile annulée + disque de poussière gauche + planète gauche |
| Droite | 0° | 180° | 270° | 90° | étoile annulée + disque de poussière droite + planète droite |
Simulation Darwin
Simulation d'une observation Darwin de 60 h sur un système solaire à 10 pc de nous.
Crédit :
Bertrand Mennesson
Imagerie différentielle
Présentation
L'idée de base de l'imagerie différentielle est de prendre plusieurs images de l'étoile et de sa planète (ou ses planètes) et de profiter des différences entre les images de ces objets pour les identifier et les distinguer.
Après l'acquisition des données brutes par l'instrument, il faut commencer par les corriger des biais instrumentaux, de la réponse des pixels du capteur CCD, on obtient alors les images dites scientifiques. Il faut ensuite corriger les effets de l'instrument (on appelle cela déconvoluer l'image de l'étoile (selon la PSF, ou Point Spread Function de l'instrument, c'est-à-dire l'étalement d'un point source sur le détecteur). Pour ce faire, plusieurs méthodes sont possibles suivant l'instrument.
ADI
L'imagerie différentielle angulaire (ADI en anglais), va exploiter la rotation des objets sur la voûte céleste, comme vous pouvez le voir sur cette [ animation ].
Les étoiles présentent un déplacement apparent dans le ciel au cours de la nuit suivant des arcs de cercle centrés sur le pôle céleste. En général, un télescope moderne compense cette rotation automatiquement, mais ici nous bloquons cette rotation et suivons seulement le déplacement apparent de l'étoile sans rotation de l'instrument. Cela a pour effet d'appliquer une rotation de l'image de la planète (à ne pas confondre avec la révolution de la planète autour de son étoile) dans le ciel autour de l'axe de rotation de la Terre. Il "suffit" alors de faire la médiane des différentes images pour annuler les signaux non fixes (comme les éventuelles planètes), ce qui revient à ne garder que la PSF de l'étoile (ponctuelle) comme image médiane. Ensuite on soustrait cette PSF de toutes les images scientifiques, puis on applique une rotation de sens opposée à celle observée sur les images de façon à corriger la rotation sur le ciel, et finalement on additionne les images pour faire ressortir les planètes (si il y en a).
ADI

Exemple de ce que permet l'imagerie différentielle angulaire : (a) une des images prise de l'étoile HD 691 avec un coronographe. Les images (b) et (c) sont le résultat de l'ADI appliquée sur deux groupes d'images. (d) est l'image finale qui est la médiane de toute les images résiduelles (comme (b), (c)). Remarquez le point source au-dessus de l'étoile qui était complètement invisible dans l'image (a).
Polarisation
La lumière émise par les étoiles n'est pas polarisée, mais quand celle-ci est diffusée ou réfléchie par des disques ou des planètes elle peut acquérir une polarisation LIEN VERS GRAIN POLARISATION. Forts de ce constat, nous pouvons prendre deux images acquises avec deux polariseurs dans des directions perpendiculaires. L'étoile apparaît inchangée, tandis que les sources secondaire par réflexion ou diffusions présenteront des différences. On peut dont soustraire l'une des images à l'autre pour ne garder que les disques et les planètes proches.
Imagerie différentielle spectrale
Les planètes et les étoiles émettent des spectres caractéristiques, comportant des raies spectrales diverses selon la physico-chimie de ces objets (température, gravité, composition). Dans certaines bandes de longueurs d'onde, seul l'un des deux types de corps possède des absorbants : c'est par exemple le cas du méthane pour les planètes (du moins celles assez froides pour que des molécules puissent exister dans leurs atmosphères). Les tavelures, quant à elles, apparaissent à une distance angulaire proportionnelle à la longueur d'onde. L'imagerie différentielle spectrale (SDI en anglais) part du principe que l'on acquiert plusieurs images, simultanément, dans plusieurs bandes de longueurs d'onde judicieusement choisies. On ajuste ensuite leur échelle relative afin de pouvoir identifier et de retirer les tavelures. Ceci nous permet d'exploiter les différences entre étoiles et planètes pour extraire des informations sur ces dernières.
Spectroscopie
Pésentation
Acquérir une image de la planète, dans différentes bandes spectrales, permet d'obtenir quelques informations sur celle-ci. Mais ces informations sont dégénérées, c'est-à-dire que plusieurs jeux de paramètres physiques vont pouvoir correspondre aux différentes images observées. Ces dégénérescences peuvent être en partie levées si l'on obtient un véritable spectre de la planète (avec une résolution spectrale suffisante), ce qui explique pouquoi les instruments qui sont mis en service depuis 2013 (SPHERE, GPI, Project 1640, etc.) soient conçus pour en obtenir.
Acquisition
Pour ce faire, ces instruments comportent un IFS (Integral Field Spectrograph), qui va disperser spectralement la lumière censée arriver sur chaque pixel.
Ainsi, au lieu d'avoir une image en deux dimensions comme pour l'imagerie pure, on obtient un cube spectral (une image en 3 dimensions) : les deux coordonnées de position sur la grille des pixels et la troisième coordonée selon la longueur d'onde observée. Une coupe du cube selon les dimensions horizontales donnera une image à la longueur d'onde de la "tranche" choisie, tandis qu'une ligne à position spatiale donnée suivant la dimension spectrale donnera le spectre observé en ce point de l'image. L'observable brut obtenu est donc un cube correspondant au flux reçu par le capteur CCD en fonction de la position du pixel et de la longueur d'onde.
Exemple de cube

Succession temporelle de différentes "tranches spectrales" correspondant aux différentes longueurs d'onde d'un cube spectral (les abscisses et les ordonnées correspondent aux coordonnées spatiales des pixels). Remarquez que le spectre de la planète (le point qui apparaît en bas à gauche à la moitié de l'animation) n'apparaît que à certaines longueurs d'ondes à une position spatiale donnée, alors que les autres éléments (artefacts, tavelures) s'éloignent en fonction de la longueur d'onde.
Réduction des données
Il faut retirer des cubes spectraux les artefacts lumineux provenant de l'étoile et les tavelures pour pouvoir localiser les éventuelles planètes.
Déconvolution spectrale
Les artefacts proviennent des phénomènes d'interférence et de diffraction qui ont lieu le long du chemin optique, leurs positions vont changer proportionnellement à la longueur d'onde. Il est donc possible d'effectuer un changement d'échelle du cube suivant la longueur d'onde pour superposer toutes les images d'une tavelure en fonction de la longueur d'onde (dans ce nouveau cube où toutes les longueurs d'onde sont ramenées à la même échelle c'est désormais l'image de la planète qui va changer de position suivant la longueur d'onde). Il est alors possible de déterminer la forme exacte des tavelures et artefacts (indépendante de la longueur d'onde dans ce cube mis à l'échelle). On peut alors remettre les tavelures et artefacts seuls à lPuis on cherche quelle est la forme du flux en fonction de la longueur d'onde, et on retire les pixels
où elle apparaît.
Enfin on change à nouveau l'échelle du cube à sa valeur initiale pour toutes les longueurs d'onde.

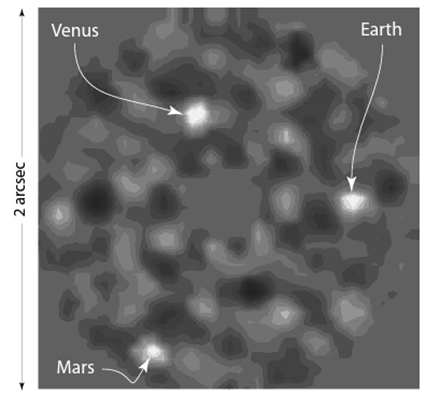
1. En décomposant un cube d'observation acquis par un IFS, on observe sur chaque tranche la planète (disque en bas à gauche de l'étoile jaune) noyée dans des tavelures (nuage rouge). La position d'un tavelure par rapport au centre va évoluer proportionnelement à la longueur d'onde. La position de la planète reste fixe.
2. Si on change l'échelle de chaque tranche en contractant chaque image proportionnelement à la longueur d'onde, les tavelures seront à position fixée d'une tranche à l'autre. C'est en revanche la planète qui va maintenant changer de position en fonction de la longueur d'onde.
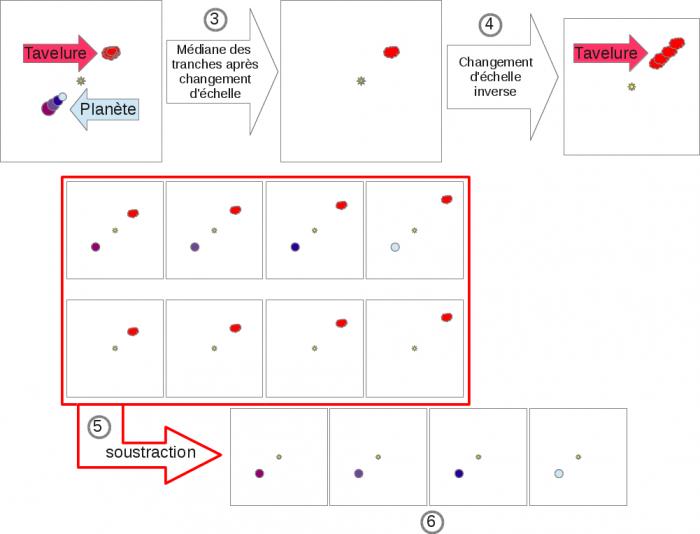
3. Si on calcule la médiane des images fabriquées à l'étape n°2, on va obtenir une image comportant les tavelures mais pas la planète car la position de la planète n'est pas la même sur toutes les images.
4. On peut alors effectuer une transformation d'échelle inverse de celle effectuée à l'étape n°2 pour obtenir la position des tavelures seules à chaque longueur d'onde.
5. On soustrait ces nouvelles images aux observations.
6. Il ne reste plus alors que l'image de la planète à chaque longueur d'onde.
Extraction du spectre
Dans ce cube, débarrassé des tavelures, on peut maintenant chercher les spectre d'une ou plusieurs planètes.
Pour faire cela on effectue une corrélation croisée avec un jeu de spectres synthétiques sur chaque pixel et on se concentre sur les meilleurs coefficients de corrélations.
On extrait ensuite le spectre de la planète identifié si elle existe.
Restrictions sur la séparation observable
On a déjà vu qu'il fallait une séparation angulaire minimale pour pouvoir imager une planète, du fait de la proximité de l'étoile bien plus brillante. En pratique, pour les instruments modernes, cette séparation minimale est de l'ordre du dixième de seconde d'arc. Attention cependant, la zone du capteur CCD où l'optique adaptative est efficace est restreinte à une petite partie du champ de vue. Les techniques de recherche d'objets se focalisent ainsi sur une zone restreinte... Pour l'instrument SPHERE, par exemple, on peut considérer que l'on recherche des planètes entre 0,1" et 3". Les planètes trop loin de leur étoile hôte sont donc difficiles à imager !
Confirmation
Auteur: JLB
Deux époques
Avoir une cible qui se comporte lors d'une observation comme une exoplanète ne suffit pas à annoncer la découverte d'une exoplanète. On recense avec le satellite Kepler 4234 candidats, en juillet 2014, et (seulement ?) 977 exoplanètes confirmées. Dans le cas de l'imagerie directe, une première détection ne suffit pas à annoncer la découverte d'une exoplanète, il en faut au moins deux pour prouver que l'objet en question est lié gravitationnellement
à une étoile, et cela permet de se faire une idée de l'orbite de l'objet. Le problème étant que les planètes détectées en imagerie directe sont éloignées de leurs étoiles et donc ont un mouvement autour de leur étoile très lent, il faut attendre plusieurs mois voire années pour obtenir des positions significativement différentes !
En effet, la source lumineuse que l'on observe à côté de l'étoile (un possible candidat planétaire), peut, en définitive, se révéler être une étoile située plus loin sur la ligne de visée (une étoile de champ), ou bien une zone plus dense que la moyenne dans le disque autour de l'étoile. En imagerie directe il faut au moins deux observations de l'objet, avec des images différentes, cohérentes avec une orbite képlérienne et un masse minimale inférieure à 13 masses de Jupiter, pour confirmer la présence d'une exoplanète. On peut alors déclarer la détection d'un objet lié à l'étoile et de masse planétaire (au dessus de 13 masses de Jupiter on entre dans le domaine des naines brunes).
Une planète tournant autour d'une étoile
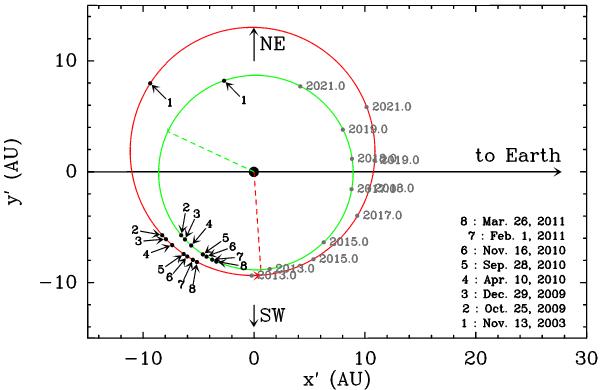
Gaël Chauvin et collaborateurs dans un article de 2012 de
Astronomy and Astrophysics présente une étude de l'orbite de
β Pictoris b
Ici nous avons une compilation de huit observations qui montre bien que l'objet tourne autour de l'étoile. Remarquez la différence de date et de position entre les point 1 et 2 : en 2003 les chercheurs ont découvert un objet proche de l'étoile mais ils ont dû attendre 2009 pour avoir la preuve que c'était bien une planète.
Autres méthodes
Une autre grande inconnue laissée par l'imagerie directe est la masse de la planète, paramètre essentiel qui va déterminer si l'objet est une planète ou une naine brune ! Or, si l'on se restreint à l'imagerie
directe, seule l'utilisation de modèles plus ou moins bien contraints permettent d'en estimer une.
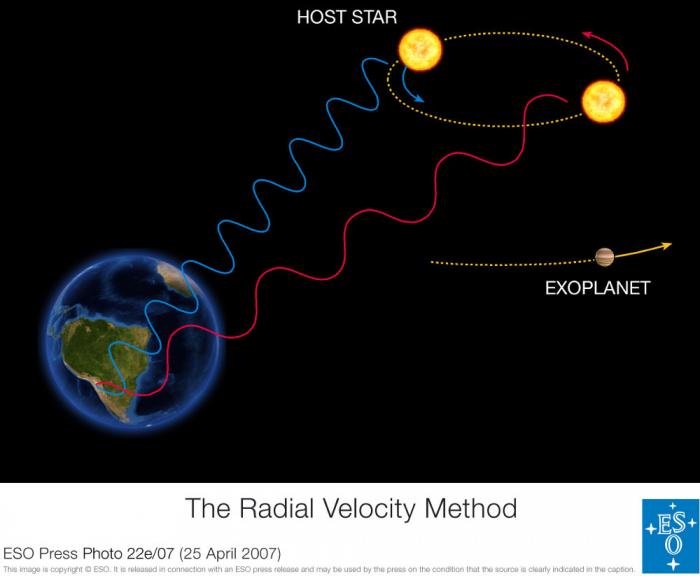
Représentation de la modification du spectre d'une étoile, décalé vers le bleu ou vers le rouge, suivant que la planète s'éloigne ou s'approche de nous, c'est ce décalage qui est utilisé par la méthode de vélocimétrie radiale.
Une mesure, indirecte, en vitesse radiale ou en astrométrie, si celles-ci sont possibles, permettraient de contraindre la masse de la cible ainsi que sa période de révolution autour de l'étoile..
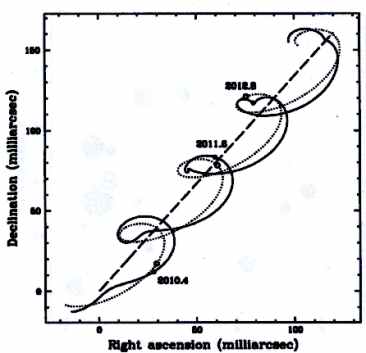
Crédit :
Évolution de la position d'une étoile dans le ciel, les petits écarts (au chemin en pointillés) viennent de la présence d'un planète, ce sont ces écart que recherche l'astrométrie pour les exoplanètes.
Michael Perryman,arxiv:1209.3563
[Cours sur la technique des vitesses radiales.]
[Cours sur la technique des vitesses radiales.]
Le cas de Fomalhaut b
C'est autour de l'étoile Fomalhaut que se trouve un objet, peut-être encore sujet à controverse.
En effet dans le disque d'accrétion de cette étoile, on a annoncé avoir trouvé dans des images visibles du HST
une planète.
Mais les images prises par Spitzer en infrarouge ne montrent rien ! Pour les défenseurs de la
"découverte", c'est que la planète est trop petite pour être vue par Spitzer. Pour les détracteurs de cette "découverte"
un objet vu en visible mais pas en infrarouge, ne peut pas être une planète.



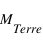 (1
(1 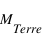 correspondant à une fois la masse Terre) , l'accrétion de gaz augmente brutalement pour former une planète géante.
correspondant à une fois la masse Terre) , l'accrétion de gaz augmente brutalement pour former une planète géante.

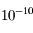 et que le disque s'étend de 5 à plusieurs centaines d'UA.
Il existe des étoiles autour desquelles on trouve un disque plus de 1200 fois plus brillant, comme η Corvi !
et que le disque s'étend de 5 à plusieurs centaines d'UA.
Il existe des étoiles autour desquelles on trouve un disque plus de 1200 fois plus brillant, comme η Corvi !

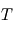 . La longueur d'onde
. La longueur d'onde 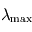 où ce spectre atteint son maximum est donnée par la loi de Wien:
où ce spectre atteint son maximum est donnée par la loi de Wien: 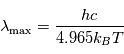 .
. 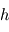 ,
, 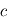 et
et 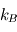 désignent respectivement les constantes de Planck, la vitesse de la lumière et la constante de Boltzmann. Un corps chaud présente donc un pic d'émission décalé vers les courtes longueurs d'onde par rapport à un corps plus froid. Aux températures ambiantes, ce pic est dans l'infrarouge (dit infrarouge thermique), mais pour des corps atteignant une température plusieurs milliers de Kelvins, ce maximum se décale dans le spectre visible : c'est le cas des étoiles par exemple, ou bien d'un tison chauffé à blanc.
désignent respectivement les constantes de Planck, la vitesse de la lumière et la constante de Boltzmann. Un corps chaud présente donc un pic d'émission décalé vers les courtes longueurs d'onde par rapport à un corps plus froid. Aux températures ambiantes, ce pic est dans l'infrarouge (dit infrarouge thermique), mais pour des corps atteignant une température plusieurs milliers de Kelvins, ce maximum se décale dans le spectre visible : c'est le cas des étoiles par exemple, ou bien d'un tison chauffé à blanc.
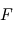 (intégré sur toutes les longueurs d'onde) émis par un corps noir ne dépend également que de sa température, suivant la loi de Stefan-Boltzmann :
(intégré sur toutes les longueurs d'onde) émis par un corps noir ne dépend également que de sa température, suivant la loi de Stefan-Boltzmann : 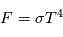 où
où 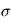 désigne la constante de Stefan-Boltzmann. Un corps chaud rayonne donc bien davantage qu'un corps froid.
désigne la constante de Stefan-Boltzmann. Un corps chaud rayonne donc bien davantage qu'un corps froid.
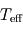 ) de la planète. Elle est en règle générale voisine de la température physique de la région de la planète d'où est principalement issue l'émission thermique (atmosphère, voire surface solide pour des planètes telluriques dotées d'une atmosphère mince).
) de la planète. Elle est en règle générale voisine de la température physique de la région de la planète d'où est principalement issue l'émission thermique (atmosphère, voire surface solide pour des planètes telluriques dotées d'une atmosphère mince).




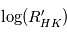 : plus il est élevé, plus l'activité est grande. Les courbes représentes plusieurs tentatives pour déterminer une relation entre ces deux observables.
: plus il est élevé, plus l'activité est grande. Les courbes représentes plusieurs tentatives pour déterminer une relation entre ces deux observables.

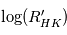 et le rayonnement en X .
B-V est l'indice de couleur des étoiles qui peut donc être relié à leur type spectral.
et le rayonnement en X .
B-V est l'indice de couleur des étoiles qui peut donc être relié à leur type spectral.

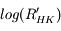 et la rotation de l'étoile exprimée par le
et la rotation de l'étoile exprimée par le 
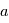 (voir la partie mécanique) et de la distance séparant le système exoplanétaire de l'observateur terrestre
(voir la partie mécanique) et de la distance séparant le système exoplanétaire de l'observateur terrestre 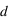 .
Or, si l'on prend un cas typique d'un planète à 100 UA autour d'un étoile située à 10 pc de nous, le rapport
.
Or, si l'on prend un cas typique d'un planète à 100 UA autour d'un étoile située à 10 pc de nous, le rapport 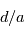 vaut plus de cent mille ! La séparation angulaire
vaut plus de cent mille ! La séparation angulaire 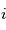 entre l'étoile et l'exoplanète vues depuis la Terre est alors donnée simplement par la formule trigonométrique
entre l'étoile et l'exoplanète vues depuis la Terre est alors donnée simplement par la formule trigonométrique 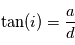 . Comme
. Comme 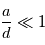 , cette formule se simplifie en
, cette formule se simplifie en 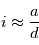 si l'on mesure
si l'on mesure 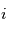 en radians (il faudra alors le convertir en secondes d'arc :
en radians (il faudra alors le convertir en secondes d'arc : 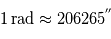 ).
).
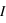 entre l'étoile et la planète grâce au contraste, définit comme :
entre l'étoile et la planète grâce au contraste, définit comme :
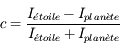

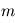 est liée au flux spectral émis ou réfléchi
est liée au flux spectral émis ou réfléchi 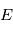 par la formule
par la formule 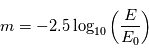 où
où 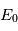 est le flux spectral d'une étoile de référence (par défaut Véga) qui correspond arbitrairement à une magnitude de 0.
est le flux spectral d'une étoile de référence (par défaut Véga) qui correspond arbitrairement à une magnitude de 0.
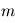 (minuscule) avec indication optionnelle d'une bande spectrale (ainsi un objet observé dans un filtre V, correspondant à la bande "visible" autour de 551 nm, verra sa magnitude apparente notée
(minuscule) avec indication optionnelle d'une bande spectrale (ainsi un objet observé dans un filtre V, correspondant à la bande "visible" autour de 551 nm, verra sa magnitude apparente notée 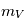 ou même
ou même 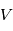 )
)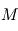 (majuscule) :
(majuscule) : 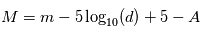 avec
avec 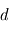 la distance séparant l'observateur de l'objet en parsec et
la distance séparant l'observateur de l'objet en parsec et 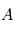 un facteur de correction provenant de l'absorption par le milieu interstellaire, négligeable sur les courtes distances. Si on consiodère la même bande spectrale que dans l'exemple précédent, la magnitude absolue sera notée
un facteur de correction provenant de l'absorption par le milieu interstellaire, négligeable sur les courtes distances. Si on consiodère la même bande spectrale que dans l'exemple précédent, la magnitude absolue sera notée 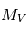 .
.






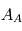 de l'étoile avant l'entrée dans l'instrument de diamètre
de l'étoile avant l'entrée dans l'instrument de diamètre 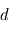 et sa phase
et sa phase 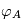 , alors la phase du rayon provenant de la position
, alors la phase du rayon provenant de la position 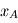 sur le plan A, vu à la position angulaire
sur le plan A, vu à la position angulaire 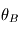 au niveau du plan B est donnée par
au niveau du plan B est donnée par 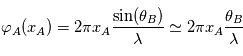 dans l'approximations de Gauss (petits angles hors-axe).
dans l'approximations de Gauss (petits angles hors-axe).
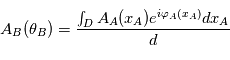 ou, en omettant le facteur de normalisation :
ou, en omettant le facteur de normalisation : 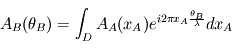 . L'amplitude de lumière reçue dans l'instrument, venant de l'étoile, est donc dépendante du diamètre
. L'amplitude de lumière reçue dans l'instrument, venant de l'étoile, est donc dépendante du diamètre 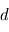 de l'instrument et de la longueur d'onde d'observation
de l'instrument et de la longueur d'onde d'observation 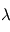 .
.

 où
où 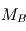 est la fonction de transmission du masque placé en B. Dans le cadre d'un coronographe,
est la fonction de transmission du masque placé en B. Dans le cadre d'un coronographe, 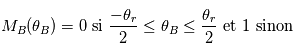 . L'amplitude au niveau du plan C va être donc être atténuée par rapport à celle au niveau du plan B, ce rapport dépendant de celui entre la taille angulaire du masque
. L'amplitude au niveau du plan C va être donc être atténuée par rapport à celle au niveau du plan B, ce rapport dépendant de celui entre la taille angulaire du masque 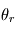 et l'ouverture
et l'ouverture 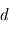 de l'instrument.
de l'instrument.
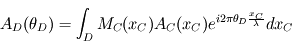 où
où 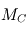 est la fonction du transmission du Lyot-Stop, un diaphragme dont on considérera la fonction de tranmission également rectangulaire :
est la fonction du transmission du Lyot-Stop, un diaphragme dont on considérera la fonction de tranmission également rectangulaire : 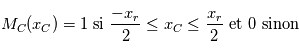 .
.
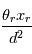 : plus le masque sera grand et le Lyot-Stop fermé, plus la lumière de l'étoile sera "éteinte" et donc plus facilement la planète sera visible. Attention toutefois, la lumière provenant d'une éventuelle planète doit quant à elle être transmise ! Il faut donc trouver un compromis entre la diminution d'intensité de la lumière de l'étoile et la conservation de l'intensité en provenance d'une éventuelle planète, dont on ne connaît pas a priori la séparation angulaire avec l'étoile...
: plus le masque sera grand et le Lyot-Stop fermé, plus la lumière de l'étoile sera "éteinte" et donc plus facilement la planète sera visible. Attention toutefois, la lumière provenant d'une éventuelle planète doit quant à elle être transmise ! Il faut donc trouver un compromis entre la diminution d'intensité de la lumière de l'étoile et la conservation de l'intensité en provenance d'une éventuelle planète, dont on ne connaît pas a priori la séparation angulaire avec l'étoile...



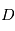 de l'instrument, l'interférométrie permet de passer d'une résolution proportionnelle à
de l'instrument, l'interférométrie permet de passer d'une résolution proportionnelle à 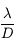 à un résolution proportionnelle à
à un résolution proportionnelle à 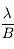 où
où 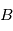 est la ligne de base d'interférométrie (dans le cas de deux télescopes, il s'agit de la distance entre ces deux télescopes). Ces télescopes éloignés sont reliés entre eux par un chemin optique conçu de telle sorte que les interférences produites par la lumière arrivant dans l'axe des télescopes (la lumière de l'étoile) conduisent à une annulation des deux ondes en provenance des deux télescopes. On obtient donc sur le récepteur une figure de franges d'interférences centrées sur l'étoile au coeur d'une frange sombre. Mais la planète, elle, est située hors-axe : elle apparaît donc légèrement décalée et, si la figure d'interférences est correctement mis en place, échappe non seulement aux interférences destructives mais profite même d'interférences constructives pour augmenter le signal.
est la ligne de base d'interférométrie (dans le cas de deux télescopes, il s'agit de la distance entre ces deux télescopes). Ces télescopes éloignés sont reliés entre eux par un chemin optique conçu de telle sorte que les interférences produites par la lumière arrivant dans l'axe des télescopes (la lumière de l'étoile) conduisent à une annulation des deux ondes en provenance des deux télescopes. On obtient donc sur le récepteur une figure de franges d'interférences centrées sur l'étoile au coeur d'une frange sombre. Mais la planète, elle, est située hors-axe : elle apparaît donc légèrement décalée et, si la figure d'interférences est correctement mis en place, échappe non seulement aux interférences destructives mais profite même d'interférences constructives pour augmenter le signal.

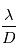 . Il faut donc augmenter la taille du télescope, ou combiner le flux de plusieurs télescopes comme nous le présentons ici. On peut alors aisément obtenir une ligne de base de 100 m en séparant 2 télescopes de cette distance.
. Il faut donc augmenter la taille du télescope, ou combiner le flux de plusieurs télescopes comme nous le présentons ici. On peut alors aisément obtenir une ligne de base de 100 m en séparant 2 télescopes de cette distance.
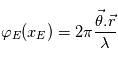 où
où 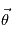 désigne l'écart sur le ciel entre la planète et l'étoile (donc dans une direction normale à l'axe optique), et
désigne l'écart sur le ciel entre la planète et l'étoile (donc dans une direction normale à l'axe optique), et 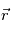 est la séparation entre la planète et l'étoile dans la direction de l'axe optique.
est la séparation entre la planète et l'étoile dans la direction de l'axe optique.