| Introduction | Structures planétaires | Observables | Techniques et méthodes | Lieux de vie | Auteurs | Boite à outils |
Analyse des simulations |
Pour chaque simulation, 60 pas de temps ont été stockés, avec une écriture de 1m 20s entre deux pas de temps :
Calculer le temps nécessaire pour effectuer une simulation.
Le coefficient de super-rotation est le rapport entre le vent zonal et la vitesse du sol due à la rotation de la planète. Comment exprime-t-on ce coefficient en fonction du vent et des caractéristiques de la planète ?
Calculer la taille occupée sur le disque par toutes les simulations.
Le calcul a été effectué grâce à un processeur cadencé à 3.6 GHz. Donner des arguments qui expliquent pourquoi les simulations ont été précalculées avant que vous ne les utilisiez. Quel est l'inconvénient ?
Un rappel newtonien a été utilisé pour simuler la partie physique. Cela consiste, à chaque appel à la physique, à relaxer le champ de température vers une température de référence imposée 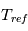 . On utilise la formulation donnée par Held & Suarez, Bulletin of the American Meteorological Society, vol. 75 , N°10, Octobre 1994. Le terme correctif est :
. On utilise la formulation donnée par Held & Suarez, Bulletin of the American Meteorological Society, vol. 75 , N°10, Octobre 1994. Le terme correctif est :
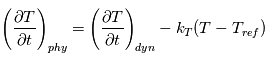
avec 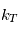 un coefficient de rappel dépendant de la latitude
un coefficient de rappel dépendant de la latitude 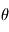 et de la coordonnée hybride
et de la coordonnée hybride 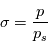 (où
(où 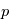 est la pression et
est la pression et 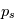 la pression de surface).
La loi pour
la pression de surface).
La loi pour 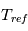 et
et 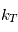 est :
est :
![T_{ref}(\theta,\sigma) = max \left[ 200, \left( 315 - 60\sin^2\theta -10 \ln (\sigma) \cos^2\theta \right) \sigma^\frac{2}{7}\right]](../pages_circulation-globale/equations_gcm-mini-projet/equation16.png)
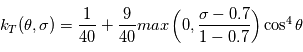
Analyser l'expression de la température de référence 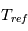 : comment varie-t-elle avec la latitude et l'altitude ?
: comment varie-t-elle avec la latitude et l'altitude ?
Physiquement, à quoi correspond 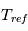 ?
?
Analyser l'expression du coefficient de rappel 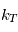 : comment varie-t-il avec la latitude et l'altitude ?
: comment varie-t-il avec la latitude et l'altitude ?
Pourquoi le rappel dépend-il ainsi de la latitude et de l'altitude ?
Comment sont représentés les jours et les saisons dans un GCM utilisant ce rappel newtonien ?
À quoi correspond la variable temporelle ?
Comment est modélisée la surface ?
Selon vous, pour quelles raisons utiliser ce rappel en lieu et place d'une physique plus complète ?