Ce mini projet vise à prendre en main un GCM à partir de résultats de simulations et d'une interface dédiée.
On se propose pour cela de voir la sensibilité d'un GCM, et tout particulièrement la circulation atmosphérique, à la période de rotation et à la taille d'une planète.
La configuration du modèle est la suivante :
- Grille longitude-latitude avec 64 points en longitude et 32 en latitude
- 15 niveaux verticaux en coordonnées pression
- Un rappel newtonien pour la physique
On se propose de voir la sensibilité de ce GCM à la période de rotation et à la taille de la planète.
Pour ce faire, on utilise 3 rayons et 6 périodes de rotations différentes, formant donc un total de 18 simulations.
Les variables disponibles en sortie sont :
- Température
- Vent zonal
- Vent méridien
- Pression de surface
- Flux de masse méridien
- Coefficient de super-rotation
Pour chaque simulation, 60 pas de temps ont été stockés, avec une écriture de 1m 20s entre deux pas de temps :
 Exercice
Exercice
Question 1)
Calculer le temps nécessaire pour effectuer une simulation.
C'est aussi simple que ça.
Question 2)
Le coefficient de super-rotation est le rapport entre le vent zonal et la vitesse du sol due à la rotation de la planète. Comment exprime-t-on ce coefficient en fonction du vent et des caractéristiques de la planète ?
Question 3)
Calculer la taille occupée sur le disque par toutes les simulations.
Combien de simulations ?
Combien de variables par simulation ?
Combien de valeurs par variables ?
Combien d'octets pas valeur ?
Question 4)
Le calcul a été effectué grâce à un processeur cadencé à 3.6 GHz. Donner des arguments qui expliquent pourquoi les simulations ont été précalculées avant que vous ne les utilisiez. Quel est l'inconvénient ?
C'est une question de temps et de mémoire.
Un rappel newtonien a été utilisé pour simuler la partie physique. Cela consiste, à chaque appel à la physique, à relaxer le champ de température vers une température de référence imposée 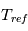 . On utilise la formulation donnée par Held & Suarez, Bulletin of the American Meteorological Society, vol. 75 , N°10, Octobre 1994. Le terme correctif est :
. On utilise la formulation donnée par Held & Suarez, Bulletin of the American Meteorological Society, vol. 75 , N°10, Octobre 1994. Le terme correctif est :
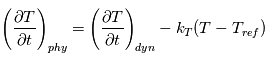
avec 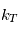 un coefficient de rappel dépendant de la latitude
un coefficient de rappel dépendant de la latitude 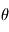 et de la coordonnée hybride
et de la coordonnée hybride 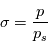 (où
(où 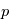 est la pression et
est la pression et 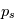 la pression de surface).
La loi pour
la pression de surface).
La loi pour 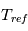 et
et 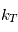 est :
est :
![T_{ref}(\theta,\sigma) = max \left[ 200, \left( 315 - 60\sin^2\theta -10 \ln (\sigma) \cos^2\theta \right) \sigma^\frac{2}{7}\right]](../pages_circulation-globale/equations_gcm-mini-projet/equation16.png)
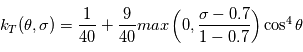
 Exercice
Exercice
Question 1)
Analyser l'expression de la température de référence 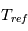 : comment varie-t-elle avec la latitude et l'altitude ?
: comment varie-t-elle avec la latitude et l'altitude ?
Physiquement, à quoi correspond 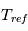 ?
?
Question 2)
Analyser l'expression du coefficient de rappel 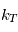 : comment varie-t-il avec la latitude et l'altitude ?
: comment varie-t-il avec la latitude et l'altitude ?
Pourquoi le rappel dépend-il ainsi de la latitude et de l'altitude ?
Question 3)
Comment sont représentés les jours et les saisons dans un GCM utilisant ce rappel newtonien ?
À quoi correspond la variable temporelle ?
Question 4)
Comment est modélisée la surface ?
Question 5)
Selon vous, pour quelles raisons utiliser ce rappel en lieu et place d'une physique plus complète ?
Il s'agit de prendre en main les données et de se familiariser avec l'exploration de champs de 2 à 6 dimensions.
 Manuel de l'utilisateur
Manuel de l'utilisateur
L'interface de GCM en ligne permet d'afficher une variable du GCM. Chaque variable possède au plus 6 dimensions, tandis qu'une figure comporte 1 à 3 dimension(s) (une dimension suivant l'axe des abscisses obligatoirement, une dimension suivant l'axe des ordonnées, et une dimension temporelle pour le défilement). En effet, un être humain peut difficilement appréhender un jeu de données à plus de 3 dimensions d'un seul coup d'oeil. Pour visualiser une variable il s'agit donc de réduire le nombre de dimensions d'une variable. Pour cela on choisira, sur une à plusieurs dimensions, une valeur ou une moyenne sur un intervalle de valeurs.
| Dimensions | Nombre de valeurs | Valeurs | Remarques | Variables |
|---|
| Température | Vents | Pression de surface | Flux de masse | Super-rotation |
| Période de rotation | 6 | 5h - 10h - 24h - 72h - 240h - 2400h | Chaque valeur correspond
à une simulation différente | X | X | X | X | X |
| Rayon de la planète | 3 | 0.5, 1 et 2 rayons terrestres | X | X | X | X | X |
| Latitude | 48 | -90° à 90° | Vu le grand nombre de points,
l'interface sélectionne la valeur
la plus proche du curseur de la réglette | X | X | X | X | X |
| Longitude | 64 | -180° à 180° | X | X | X | | X |
| Altitude | 15 | 1 bar à 0.5 mbar | Valeurs suivant une
décroissance logarithmique | X | X | | X | X |
| Temps | 60 | 0 à 60 unités | | X | X | X | | X |
 Exercice
Exercice
Question 1)
Afficher la température et la pression de surface au niveau du sol, puis à d'autres altitudes à un instant donné ou en faisant défiler les instants sur un intervalle de temps. Comment évolue le champ de pression de surface en demandant différentes altitudes ? Pourquoi ?
Question 2)
Afficher un profil vertical de température à l'équateur.
Question 3)
Afficher le champ de température et la pression de surface en moyenne zonale, puis la température et le vent zonal. Que remarquez-vous ? Pourquoi ?
Question 4)
Un diagramme de Hovmöller permet de visualiser la propagation d'ondes, en affichant un champ en fonction du temps et de la longitude ou latitude. Faire un tel diagramme sur le champ de votre choix et estimer la ou les période(s) des ondes présentes.
Question 5)
Afficher la température en fonction de la latitude et de la vitesse de rotation, à une altitude donnée et en moyenne zonale.
Question 6)
Afficher la pression de surface en fonction de la vitesse de rotation et du rayon de la planète.
 Pour aller plus loin
Pour aller plus loin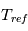 . On utilise la formulation donnée par Held & Suarez, Bulletin of the American Meteorological Society, vol. 75 , N°10, Octobre 1994. Le terme correctif est :
. On utilise la formulation donnée par Held & Suarez, Bulletin of the American Meteorological Society, vol. 75 , N°10, Octobre 1994. Le terme correctif est :
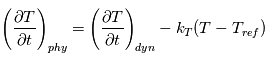
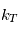 un coefficient de rappel dépendant de la latitude
un coefficient de rappel dépendant de la latitude 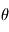 et de la coordonnée hybride
et de la coordonnée hybride 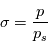 (où
(où 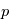 est la pression et
est la pression et 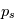 la pression de surface).
La loi pour
la pression de surface).
La loi pour 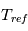 et
et 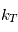 est :
est :
![T_{ref}(\theta,\sigma) = max \left[ 200, \left( 315 - 60\sin^2\theta -10 \ln (\sigma) \cos^2\theta \right) \sigma^\frac{2}{7}\right]](../pages_circulation-globale/equations_gcm-mini-projet/equation16.png)
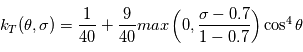
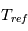 : comment varie-t-elle avec la latitude et l'altitude ?
: comment varie-t-elle avec la latitude et l'altitude ?
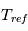 ?
?
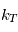 : comment varie-t-il avec la latitude et l'altitude ?
: comment varie-t-il avec la latitude et l'altitude ?