La diffusion Rayleigh

Cette diffusion est très importante dans les atmosphères planétaires. Elle se produit quand une onde vient à être diffusée par une particule qui est très petite devant sa longueur d'onde. Par exemple, quand du rayonnement visible (~500nm) vient à rencontrer une molécule dans l'air (~0.1 nm). La diffusion Rayleigh est isotrope.

L'efficacité de la diffusion Rayleigh dépend de la longueur d'onde de l'onde incidente. Plus la longueur d'onde est petite, plus la diffusion est efficace. C'est pour cela que le ciel est bleu : la lumière dans les longueurs d'onde bleues est plus diffusée et semble venir de toutes les directions, tandis que la lumière rouge est peu diffusée et traverse l'atmosphère. C'est aussi pourquoi le Soleil semble rouge au coucher : la lumière traverse plus d'atmosphère et le bleu est fortement diffusé. La lumière nous arrivant est donc pauvre en bleu et nous semble rouge-orangée.

Angles de phase et de diffusion

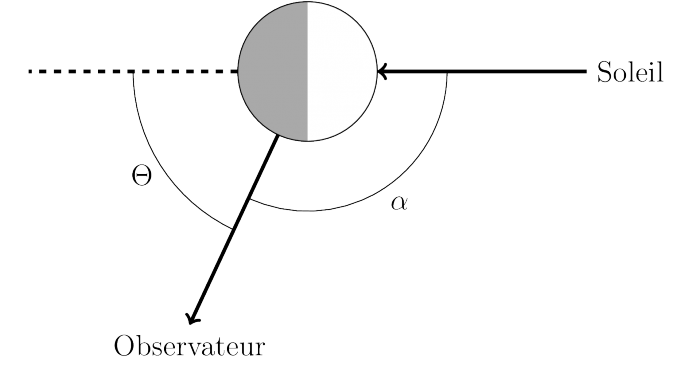
Illustration de l'angle de phase (α, entre la source, l'objet et l'observateur) et de l'angle de diffusion (Θ, entre la direction du rayon incident et celle du rayon diffusé).

Crédit : Loïc Rossi CC-BY-SA

En termes de polarisation, la diffusion Rayleigh est caractéristique en ce qu'elle polarise la lumière en fonction de l'angle de phase α. Rappelons que l'angle de phase est l'angle entre le rayon incident et l'angle émergent (c'est le supplémentaire de l'angle de diffusion). La diffusion Rayleigh diffuse la lumière avec une polarisation perpendiculaire au plan de diffusion, avec un maximum pour un angle de phase de 90°.

La diffusion de Mie

La diffusion de Mie concerne elle des photons diffusés par des particules de taille similaire ou supérieure à la longueur d'onde. Par exemple, la lumière visible (~500 nm) dans les nuages de gouttelettes d'eau (~5μm). Elle tire son nom du physicien allemand Gustav Mie qui a établi cette solution des équations de Maxwell en 1908.

Contrairement à la diffusion Rayleigh qui peut se résoudre analytiquement, la diffusion de Mie est plus complexe. Il s'agit d'une solution particulière des équations de Maxwell et a une expression analytique, mais dont les calculs sont vite fastidieux ; c'est pourquoi on l'utilise surtout avec des outils numériques.

La diffusion de Mie n'est pas isotrope : elle diffuse préférentiellement vers l'avant, et dépend peu de la longueur d'onde. C'est elle qui rend les nuages blancs : toutes les longueurs d'onde sont diffusées vers l'observateur qui voit donc un nuage blanc !

En termes de polarisation, l'émission varie beaucoup en fonction de la taille du diffuseur, de son indice de réfraction, et de la distribution en taille des diffuseurs. Mais on retrouve des structures caractéristiques :

• l'arc-en-ciel : uniquement visible pour un indice de réfraction relativement faible (par exemple pour l'eau n=1,33). Visible aussi dans les longueurs d'ondes visibles ; vous en avez sans doute déjà vu un.
• la gloire : phénomène aussi perceptible en lumière visible. On peut les observer dans la brume quand le soleil est bas, ou quand on est à bord d'un avion dont on voit l'ombre sur les nuages. Les gloires sont souvent confondues avec les halos et les arcs-en-ciel (on parle parfois de Spectre de Brocken).

Indicatrices de rayonnement

Indicatrices de rayonnement pour différents types de diffusion avec un rayon venant de la gauche. À gauche, la diffusion de Rayleigh, au centre une diffusion intermédiaire entre Rayleigh et Mie, à droite une indicatrice typique de la diffusion de Mie, avec une diffusion principalement vers l'avant.

Crédit : Sharayanan, CC-BY-SA

Quelques nuages cumulus

Si ces cumulus apparaissent blancs, c'est à cause de la diffusion de Mie.

Crédit : Michael Jastremski, CC-BY-SA

Une gloire

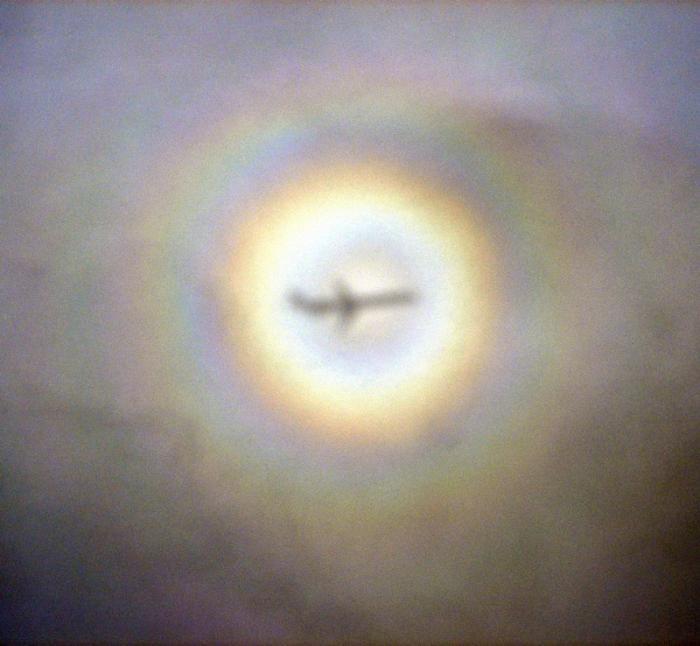
Une gloire vue depuis un avion de ligne.

Crédit : Anders Sandberg, CC-BY.