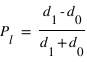Polarisation
Auteur: Loïc Rossi
- Découvrir
- Introduction
- Historique de la polarisation
- Contexte
- La polarisation
- Les types de polarisation
- La polarisation elliptique
- La polarisation circulaire
- La polarisation linéaire
- Lumière non polarisée
- Polariseurs
- Les paramètres de Stokes
- Processus polarisants
- Polarisation par diffusion
- Polarisation par diffusion : Rayleigh
- Polarisation par diffusion : Mie
- La polarisation par réflexion/transmission.
- La polarisation par transmission et réflexion
- Applications à la planétologie
- La polarimétrie dans le système solaire
- Applications à l'exoplanétologie
- Comprendre
- Réflexion et transmission
- Interfaces entre deux milieux
- Polarisation perpendiculaire au plan d'incidence
- Polarisation parallèle au plan d'incidence
- Coefficients de réflexion et de transmission
- Usages
- La polarisation par diffusion
- Les différents régimes
- La diffusion Rayleigh
- Exercices
- Mini-projet
- Mini-projet : les gloires de Vénus
- Mini-projet : les gloires de Vénus
-
Polarisation
 Objectif
Objectif
L'objectif de ce chapitre est de découvrir la polarisation de la lumière, ses utilisations et comment elle nous apporte des informations sur les propriétés des environnements planétaires.
 Pré-requis
Pré-requis
Dans ce grain, les concepts d'ondes et en particulier d'onde électromagnétique seront employés. Avoir une connaissance élémentaire de ces concepts est donc recommandée.
Cliquez ici pour commencer le chapitre.
 Illustrations et figures
Illustrations et figures
Sauf mention spécifique les illustrations et figures utilisées dans ce cours sont librement utilisables, étant issues du domaine public ou publiées sous une licence Creative Commons .
Découvrir
Auteur: Loïc Rossi
Introduction
Auteur: Loïc Rossi
Historique de la polarisation
 La découverte et l'étude de la polarisation
La découverte et l'étude de la polarisation
Rasmus Bartholin (1625-1698) publie en 1669 ses observations des propriétés
optiques du Spath d'Islande. Il avait remarqué qu'un rayon réfracté par un tel
cristal produisait deux rayons, un rayon « ordinaire » et un rayon
« extraordinaire ». Les deux rayons ayant des propriétés différentes : c'est la découverte de la biréfringence.
Christian Huygens (1629-1695) étudiera aussi la double réfringence des cristaux
de spath, et observera que l'intensité de la lumière transmise par deux cristaux dépend de
l'orientation de ces derniers. Il y a donc une asymétrie autour de la direction
de propagation : ce sont les bases de la polarisation.
François Arago (1786-1853) s'intéressera lui à la polarisation du ciel. Dans la
même période, Étienne-Louis Malus (1775-1812) publie en 1809 des travaux sur
la polarisation de la lumière par réflexion : il avait observé que la lumière
du Soleil couchant observée après réflexion puis à travers un cristal
biréfringent changeait d'intensité avec la rotation du cristal. En 1810, il
publie ses travaux sur la biréfringence, qui lui valent le prix de l'Académie
des Sciences. Il est le premier à employer le terme de « polarisation ».
François Arago

(1786-1853)
Dans la lignée des observations de Malus, David Brewster (1781-1868) établit
en 1815 les lois de la polarisation par réflexion, avec notamment l'angle qui porte son
nom : l'angle de Brewster.
Augustin Fresnel (1778-1827) observera que les faisceaux ordinaires et
extraordinaires produits par biréfringence ne peuvent pas produire
d'interférences (car de différentes polarisations), ce qui lui permettra d'établir que la lumière est une onde
transverse, et non longitudinale.
En 1845, Michael Faraday (1791-1867) réalise une expérience où il fait
traverser un faisceau de lumière polarisée linéairement dans un matériau exposé
à un champ magnétique orienté dans la direction de propagation de la lumière.
Faraday observe que la direction de polarisation à la sortie du matériau est
changée, prouvant l'effet d'un champ magnétique sur la lumière, et confirmant
ainsi que la lumière est une onde électromagnétique.
La synthèse de ces divers travaux sur la lumière et la polarisation viendra avec
James Clerk Maxwell (1831-1879) qui achèvera de construire la théorie
électromagnétique avec les équations de Maxwell publiées sous diverses formes
entre 1865 et 1873.
James Clerk Maxwell

(1831-1879)
Pieter Zeeman (1865-1943) découvrira en 1896 l'élargissement et la polarisation des
raies d'émission spectrales sous l'effet d'un champ magnétique.
D'autre part, John Wiliam Strutt (Lord Rayleigh) (1884-1919) publie en
1871 ses travaux sur la diffusion (diffusion Rayleigh) de la lumière par de petites particules,
expliquant ainsi la couleur et la polarisation du ciel.
Toujours concernant la diffusion, Gustav Mie (1869-1957) établira la solution
des équations de Maxwell dans le cas de la diffusion par particules sphériques,
ce régime se situant entre le régime de Rayleigh et l'optique géométrique.
Un héritage important
La découverte de la polarisation et son étude ont ouvert un champ d'étude important que les sciences planétaires ont su exploiter, comme nous allons le voir dans le cadre de ce chapitre. Nous ne traiterons pas tous les phénomènes liés à la polarisation mais nous nous focaliserons sur ceux utiles à la planétologie.
Contexte
 Pourquoi la polarisation ?
Pourquoi la polarisation ?
La principale observable pour un astronome ou un astrophysicien, c'est le photon, qui peut être considéré comme la particule de lumière. Le photon est porteur de beaucoup d'informations, car il est modifié par les diverses interactions qu'il peut avoir avec son environnement. Ainsi, divers processus peuvent changer la polarisation de la lumière, et fournir ainsi des informations sur la surface, l'atmosphère et d'autres paramètres des systèmes planétaires.
Les processus polarisants peuvent concerner une large gamme de longueurs d'ondes. De plus les dispositifs de mesure de la polarisation peuvent être passifs et assez simples à mettre en œuvre.
 La polarisation autour de soi
La polarisation autour de soi
Dans la vie quotidienne, on est régulièrement amené à rencontrer des dispositifs ou des phénomènes polarisants. Quelques exemples communs :
- Les affichages à cristaux liquides (aussi appelés LCD, présents dans les montres numériques ou les écrans d'ordinateurs) utilisent des dispositifs polarisants ;
- les systèmes de vision en 3D passive des cinémas utilisent souvent des lunettes à verres polarisés ;
- la réflexion de la lumière sur la route ou sur une vitre peut générer de la lumière polarisée.
Mais la nature n'est pas en reste :
- Certains insectes utilisent la polarisation pour s'orienter, en utilisant la polarisation de la lumière diffuse du ciel ;
- en chimie, les molécules chirales polarisent la lumière différemment selon leur configuration et leur orientation ;
- les minéraux peuvent aussi polariser la lumière grâce à des propriétés de biréfringence.
La polarisation
Auteur: Loïc Rossi
Les types de polarisation
La polarisation est une propriété de la lumière. Cette dernière est une onde électromagnétique se déplaçant dans le vide à la vitesse c=299 792 458 m/s. Elle est composée d'un champ électrique (noté généralement E) et d'un champ magnétique (noté B), orthogonaux. À travers les équations de Maxwell, les champs E et B sont liés : la connaissance de l'un suffit pour connaitre l'autre. Aussi, pour simplifier — et c'est aussi la convention choisie en polarimétrie — on ne raisonne que sur le champ E.
Une onde électromagnétique plane se définit notamment par sa direction de propagation. Le plan perpendiculaire à la direction de propagation est appelé le plan d'onde. C'est dans le plan d'onde qu'évolue le champ E (et le champ B, mais nous n'en parlerons plus). À chaque instant, le champ E a une amplitude et une direction différente dans le plan d'onde. Dit autrement, si l'onde se propage en direction de l'observateur ce dernier verra le champ E former differents motifs dans le plan d'onde pendant son évolution temporelle. C'est cela qui va définir la polarisation de l'onde.
Une onde électromagnétique plane
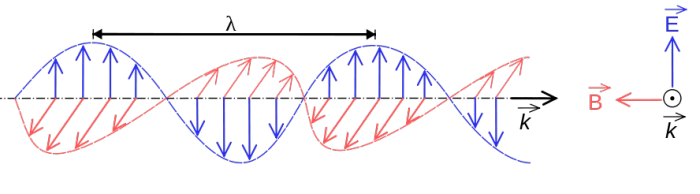
Schéma montrant une onde électromagnétique plane avec les champs E (en bleu) et B (en rouge) orthogonaux. Le vecteur k indique la direction de propagation. La longueur d'onde λ est indiquée également.
Crédit :
SuperManu, CC-BY-SA
La polarisation elliptique
Le cas le plus général est celui d'une polarisation elliptique, les autres situation pouvant être considérées comme des cas particuliers de celui-ci.
 Polarisation elliptique
Polarisation elliptique
Si le champ E dessine une ellipse dans le plan d'onde, on parle de polarisation elliptique.
C'est le cas le plus général. On peut alors décomposer le champ électrique selon deux composantes perpendiculaires :
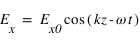
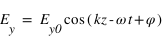 , où
, où 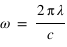 est la pulsation de l'onde électromagnétique;
est la pulsation de l'onde électromagnétique; 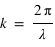 le nombre d'onde et φ le déphasage entre les deux composantes.
le nombre d'onde et φ le déphasage entre les deux composantes.
Champ E d'une onde polarisée elliptiquement.
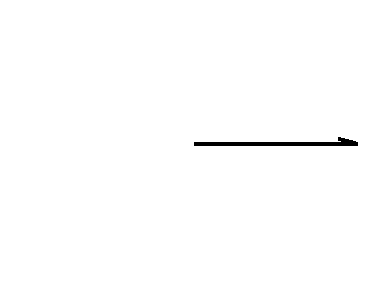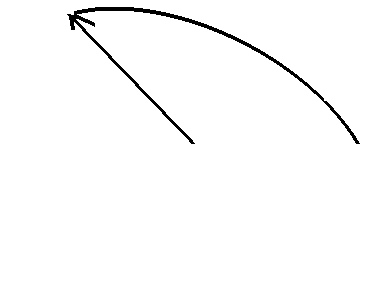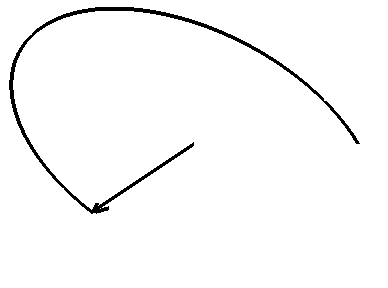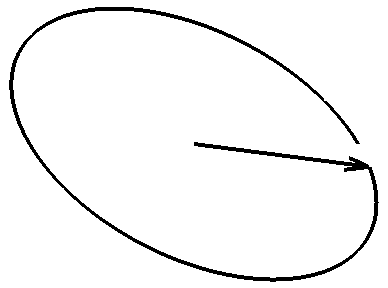
Vue du plan d'onde d'une onde électromagnétique polarisée elliptiquement. La direction de propagation « sort » de l'écran. (Cliquez sur l'image pour l'agrandir et voir l'animation)
Crédit :
Fffred
Polarisation elliptique

Onde polarisée elliptiquement. Les courbes bleue et rouge représentent les deux composantes orthogonales du champ électrique. Le champ E est indiqué en noir. La projection sur le plan d'onde (ligne jaune sur le plan bleu) donne une ellipse.
Crédit :
Inductiveload
La polarisation circulaire
Nous venons de voir la polarisation elliptique. On peut remarquer que si les deux axes principaux de l'ellipse sont égaux, l'ellipse devient un cercle : c'est la polarisation circulaire.
 Polarisation circulaire
Polarisation circulaire
Si le champ E dessine un cercle dans le plan d'onde, on parle de polarisation circulaire. Le sens de rotation de E définit une polarisation :
- Droite, si l'onde tourne dans le sens trigonométrique
- Gauche, si l'onde tourne dans le sens horaire
On peut se souvenir du sens de rotation en utilisant ses mains. En pointant son pouce vers soi, on regarde dans quel sens s'enroulent les autres doigts; en choisissant la main qui permet de reproduire le sens de rotation de l'onde polarisée (main gauche ou main droite), on détermine le sens de la polarisation !
On peut alors écrire les composantes du champ électrique comme suit :
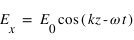
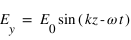 , où
, où 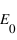 est l'amplitude commune des deux composantes du champ électrique. La phase vaut alors
est l'amplitude commune des deux composantes du champ électrique. La phase vaut alors 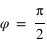 .
.
Champ E d'une onde polarisée circulairement.
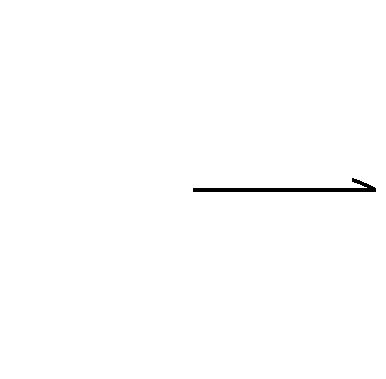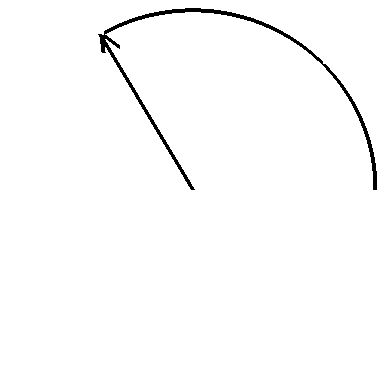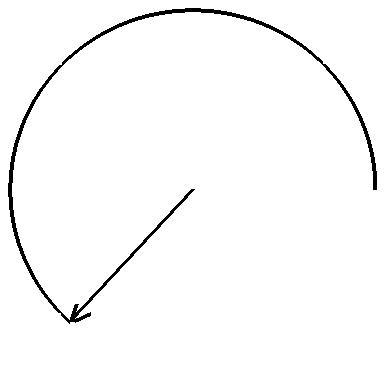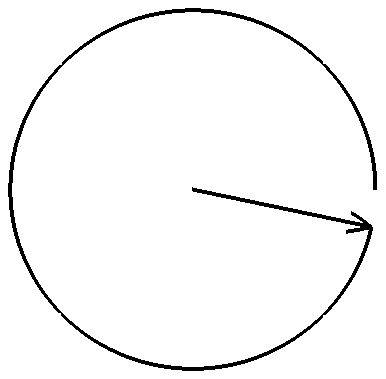
Vue du plan d'onde d'une onde électromagnétique polarisée circulairement. La direction de propagation « sort » de l'écran. Ici, la polarisation est droite vue depuis l'observateur. (Cliquer sur l'image pour l'agrandir et voir l'anumation)
Crédit :
Fffred
Polarisation circulaire

Onde polarisée circulairement. Les courbes bleue et rouge représentent les deux composantes orthogonales du champ électrique. Le champ E est indiqué en noir. La projection sur le plan d'onde (en noir sur le plan bleu) donne un cercle.
Crédit :
Inductiveload
 Attention aux conventions !
Attention aux conventions !
Attention ! Ceci est vrai si on se place du point de vue de l'observateur. Les directions doivent être interverties si on se place du point de vue de la source. Quand vous traitez des problèmes de polarisation, vérifiez toujours quelle est la convention utilisée.
La polarisation linéaire
 Polarisation linéaire
Polarisation linéaire
Si le champ E décrit un segment dans le plan d'onde, on dit que la polarisation est linéaire. On peut la voir comme une polarisation elliptique pour laquelle l'un des deux axes de l'ellipse de polarisation serait réduit à un point.
Le champ électrique s'écrit alors
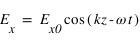
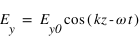 , avec
, avec 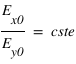 et
et 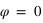 .
.
Le champ E d'une onde polarisée linéairement.

Vue du plan d'onde d'une onde électromagnétique polarisée linéairement. La direction de propagation « sort » de l'écran. (Cliquer sur l'image pour l'agrandir et voir l'animation)
Crédit :
Fffred
Polarisation linéaire

Onde polarisée linéairement. Les courbes bleue et rouge représentent les deux composantes orthogonales du champ électrique. Le champ E est indiqué en noir. La projection sur le plan d'onde (ligne jaune sur le plan bleu) donne une droite.
Crédit :
Inductiveload
Lumière non polarisée
Lumière non polarisée
On a abordé ici les types de polarisation, mais la lumière n'est pas forcément polarisée. Ou plutôt, un faisceau de lumière n'est pas polarisée d'une seule façon. On peut avoir une superposition de différentes polarisations linéaires, elliptiques et circulaires. La lumière naturelle est ainsi composée de multiples états de polarisation différents, donnant en moyenne une lumière non polarisée.
Pour les situations de polarisation linéaire, on décompose généralement la polarisation en deux composantes : la composante parallèle au plan de diffusion, et la composante qui lui est orthogonale. On représente souvent la lumière naturelle par un faisceau de lumière polarisée dans deux directions orthogonales. Un polariseur pourra alors filtrer l'une des composantes.
Lumière naturelle
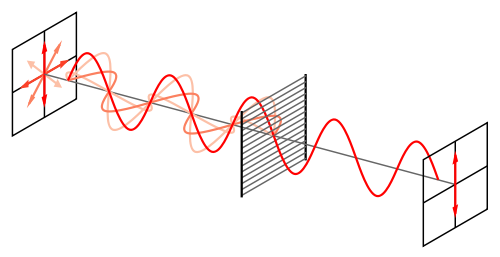
Exemple de lumière non polarisée venant de la gauche et traversant un filtre polarisant. Seule la composante polarisée linéairement et verticale est transmise.
Crédit :
Fffred CC-BY-SA
Sources non polarisées
Les sources naturellement polarisées ne sont pas communes. La lumière solaire est un bon exemple de lumière non polarisée. De même, le rayonnement thermique n'est généralement pas polarisé. Cependant, bien que les sources ne soient pas polarisées, la réflexion et la traversée de certains milieux peuvent modifier la polarisation de la lumière.
Polariseurs
Un polariseur est un dispositif qui agit sur un faisceau de lumière incidente selon la polarisation de celui-ci. Il peut filtrer la lumière en ne laissant passer que certaines composantes de polarisation. Il peut aussi changer la polarisation d'un faisceau incident.
Les filtres polarisants
La plupart des polariseurs sont de simples filtres (la marque Polaroid en est un exemple connu), qui ne laisse passer la lumière polarisée que dans une direction particulière (on parle de direction ou d'axe du polariseur). Ainsi une lumière non-polarisée sera polarisée après avoir traversé un tel filtre. Une lumière polarisée ne sera totalement transmise que si la direction de polarisation incidente est la même que celle du filtre.
L'intensité transmise par un polariseur dépend des orientations du filtre et de l'onde incidente. Si on note 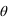 l'angle entre la direction du filtre et la direction de polarisation de l'onde incidente et
l'angle entre la direction du filtre et la direction de polarisation de l'onde incidente et 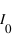 son intensité, on a après le polariseur une intensité
son intensité, on a après le polariseur une intensité 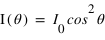 , c'est la Loi de Malus. De fait, on retrouve qu'un polariseur dont la direction de polarisation est perpendiculaire à celle de la lumière incidente, il ne transmettra rien. De même, deux polariseurs de directions perpendiculaires (on dit qu'ils sont croisés) ne laissent pas passer la lumière: celle-ci est polarisée dans une direction par le premier polariseur, puis bloquée par le second, de direction perpendiculaire. Dans le cas d'une source non polarisée
, c'est la Loi de Malus. De fait, on retrouve qu'un polariseur dont la direction de polarisation est perpendiculaire à celle de la lumière incidente, il ne transmettra rien. De même, deux polariseurs de directions perpendiculaires (on dit qu'ils sont croisés) ne laissent pas passer la lumière: celle-ci est polarisée dans une direction par le premier polariseur, puis bloquée par le second, de direction perpendiculaire. Dans le cas d'une source non polarisée 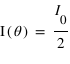 .
.
Illustration de la loi de Malus

Un polariseur (parfois appelé analyseur) devant une source polarisée linéairement . Selon l'angle que fait la direction du polariseur avec la polarisation de la lumière, le filtre laisse passer plus ou moins de lumière, conformément à la loi de Malus.
Crédit :
Rogilbert
Lames à retard
D'autres dispositifs optiques permettent de modifier la polarisation de la lumière. Les lames à retard sont utilisées à cet effet. On l'a vu précédemment, un faisceau polarisé peut être considéré comme étant la somme de deux composantes de polarisation orthogonales. Lors de la traversée d'une lame à retard, les propriétés de biréfringence de la lame vont faire qu'une des deux composantes est retardée par rapport à l'autre, ce qui va changer la polarisation en sortie. On dira que la lame a deux axes, un axe lent et un axe rapide.
Dans le cas d'une lame demi-onde, le déphasage entre les deux composantes est π (ou d'une demi-longueur d'onde, d'où son nom). De fait, si l'onde polarisée linéairement selon une direction faisant un angle θ avec l'axe rapide de la lame, elle ressortira avec une direction tournée d'un angle 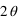 . L'utilisation principale qui en est faite est de changer la direction de polarisation linéaire. Une onde polarisée avec un angle
. L'utilisation principale qui en est faite est de changer la direction de polarisation linéaire. Une onde polarisée avec un angle 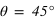 par rapport à l'axe rapide aura en sortie un angle
par rapport à l'axe rapide aura en sortie un angle 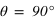 avec l'axe rapide : les directions incidentes et émergentes sont donc croisées !
avec l'axe rapide : les directions incidentes et émergentes sont donc croisées !
Lame à retard
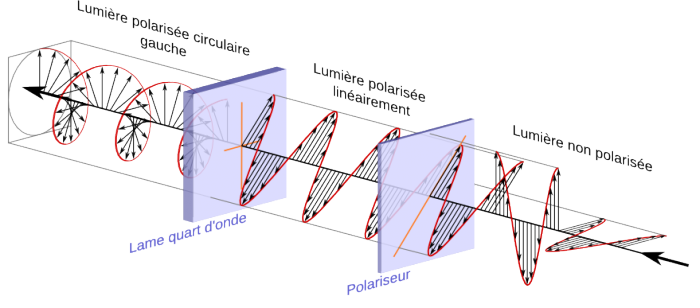
De la lumière non polarisée passe dans un polariseur qui la polarise linéairement avant de passer à travers une lame quart d'onde qui la transforme en lumière polarisée circulaire gauche.
Crédit :
Dave3457, domaine public, traduction Loïc Rossi
Dans le cas d'une lame quart d'onde, le déphasage vaut 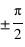 (ou un quart de longueur d'onde). Une telle lame permet de transformer une polarisation linéaire en une polarisation elliptique ou circulaire, et inversement. En effet dans le cas linéaire, les deux composantes du champ électrique, parallèle et perpendiculaire à l'axe rapide sont de la forme
(ou un quart de longueur d'onde). Une telle lame permet de transformer une polarisation linéaire en une polarisation elliptique ou circulaire, et inversement. En effet dans le cas linéaire, les deux composantes du champ électrique, parallèle et perpendiculaire à l'axe rapide sont de la forme 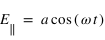 et
et 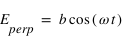 . Si on introduit un déphasage de
. Si on introduit un déphasage de 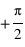 , les deux composantes deviendont
, les deux composantes deviendont 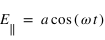 et
et 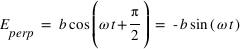 , le vecteur du champ électrique va donc décrire une ellipse !
, le vecteur du champ électrique va donc décrire une ellipse !
Attention ! Le fonctionnement des lames à retard dépend de la longueur d'onde !
Les paramètres de Stokes
Pour décrire l'état de polarisation de la lumière on va utiliser une notation introduite par Gabriel Stokes : le vecteur de Stokes. Celui-ci est composé de quatre éléments : I, Q, U et V.
Les éléments de Stokes
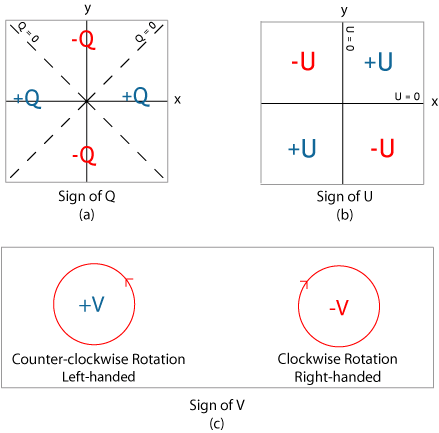
Figure illustrant les différents paramètres de Stokes.
Crédit :
Dan Moulton, CC-BY-SA
Polarisation linéaire
La polarisation linéaire est décrite par les éléments Q et U. Ils sont définis tels que (cf. figure):
Le degré de polarisation linéaire se mesure alors avec 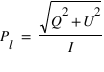 . Si on est dans le cas où
. Si on est dans le cas où 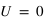 ,alors
,alors 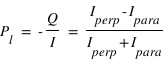 .
.
Polarisation circulaire
La polarisation circulaire se mesure avec V. Si V est positif, la polarisation est circulaire droite, si V est négatif, elle est gauche (du point de vue de la source, attention les conventions peuvent varier). Le degré de polarisation circulaire est alors simplement 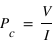 .
.
Processus polarisants
Auteur: Loïc Rossi
Polarisation par diffusion
Auteur: Loïc Rossi
Polarisation par diffusion : Rayleigh
On va maintenant s'intéresser aux processus liés aux environnements planétaires qui peuvent polariser la lumière et donc nous donner des informations sur les caractéristiques des milieux étudiés. Dans le cas où les planètes ou corps auxquels on s'intéresse ont une atmosphère, la lumière peut être polarisée par diffusion au sein de celle-ci.
La diffusion Rayleigh
Cette diffusion est très importante dans les atmosphères
planétaires. Elle se produit quand une onde vient à être diffusée par
une particule qui est très petite devant sa longueur d'onde. Par
exemple, quand du rayonnement visible (~500nm) vient à rencontrer une
molécule dans l'air (~0.1 nm). La diffusion Rayleigh est isotrope.
L'efficacité de la diffusion Rayleigh dépend de la longueur d'onde de
l'onde incidente. Plus la longueur d'onde est petite, plus la
diffusion est efficace. C'est pour cela que le ciel est bleu : la lumière dans les longueurs d'onde bleues est plus diffusée et
semble venir de toutes les directions, tandis que la lumière rouge
est peu diffusée et traverse l'atmosphère. C'est aussi pourquoi le Soleil semble rouge au coucher : la lumière traverse plus d'atmosphère et le bleu est fortement diffusé. La lumière nous arrivant est donc pauvre en bleu et nous semble rouge-orangée.
Angles de phase et de diffusion
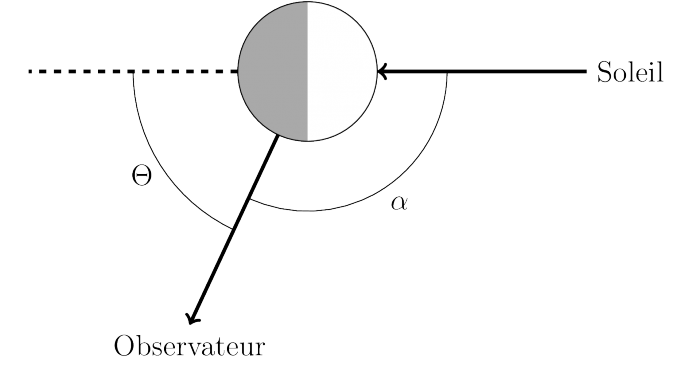
Illustration de l'angle de phase (α, entre la source, l'objet et l'observateur) et de l'angle de diffusion (Θ, entre la direction du rayon incident et celle du rayon diffusé).
Crédit :
Loïc Rossi CC-BY-SA
En termes de polarisation, la diffusion Rayleigh est caractéristique
en ce qu'elle polarise la lumière en fonction de l'angle de
phase α. Rappelons que l'angle de phase est l'angle entre le rayon
incident et l'angle émergent (c'est le supplémentaire de l'angle de
diffusion). La diffusion Rayleigh diffuse la lumière avec une
polarisation perpendiculaire au plan de diffusion, avec un maximum
pour un angle de phase de 90°.
Polarisation par diffusion : Mie
 La diffusion de Mie
La diffusion de Mie
La diffusion de Mie concerne elle des photons diffusés par des particules de taille similaire ou supérieure à la longueur d'onde. Par
exemple, la lumière visible (~500 nm) dans les nuages de gouttelettes d'eau (~5μm). Elle tire son nom du physicien allemand Gustav Mie qui a établi cette solution des équations de Maxwell en 1908.
Contrairement à la diffusion Rayleigh qui peut se résoudre
analytiquement, la diffusion de Mie est plus complexe. Il s'agit d'une
solution particulière des équations de Maxwell et a une expression
analytique, mais dont les calculs sont vite fastidieux ; c'est pourquoi on
l'utilise surtout avec des outils numériques.
La diffusion de Mie n'est pas isotrope : elle diffuse
préférentiellement vers l'avant, et dépend peu de la longueur
d'onde. C'est elle qui rend les nuages blancs : toutes les longueurs
d'onde sont diffusées vers l'observateur qui voit donc un nuage
blanc !
En termes de polarisation, l'émission varie beaucoup en fonction
de la taille du diffuseur, de son indice de réfraction, et de la
distribution en taille des diffuseurs. Mais on retrouve des structures
caractéristiques :
- l'arc-en-ciel : uniquement visible pour un indice de réfraction relativement faible (par exemple pour l'eau n=1,33). Visible aussi
dans les longueurs d'ondes visibles ; vous en avez sans doute déjà vu un.
- la gloire : phénomène aussi perceptible en lumière visible. On peut
les observer dans la brume quand le soleil est bas, ou quand on est à
bord d'un avion dont on voit l'ombre sur les nuages. Les gloires sont
souvent confondues avec les halos et les arcs-en-ciel (on parle
parfois de Spectre de Brocken).
Indicatrices de rayonnement

Indicatrices de rayonnement pour différents types de diffusion avec un rayon venant de la gauche. À gauche, la diffusion de Rayleigh, au centre une diffusion intermédiaire entre Rayleigh et Mie, à droite une indicatrice typique de la diffusion de Mie, avec une diffusion principalement vers l'avant.
Crédit :
Sharayanan, CC-BY-SA
Quelques nuages cumulus

Si ces cumulus apparaissent blancs, c'est à cause de la diffusion de Mie.
Crédit :
Michael Jastremski, CC-BY-SA
Une gloire
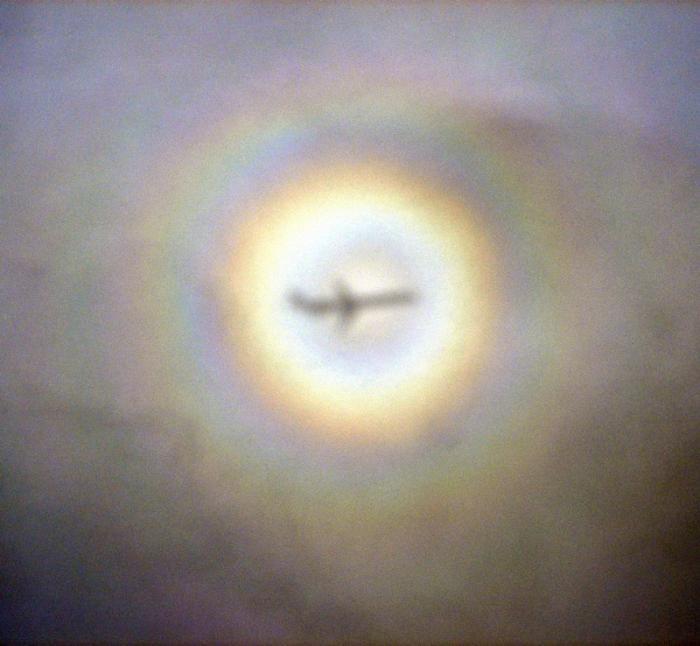
Une gloire vue depuis un avion de ligne.
Crédit :
Anders Sandberg, CC-BY.
La polarisation par réflexion/transmission.
Auteur: Loïc Rossi
La polarisation par transmission et réflexion
Certains matériaux ont des propriétés polarisantes sur la lumière les traversant, notamment par biréfringence.
 La biréfringence
La biréfringence
La biréfringence est une propriété de certains matériaux dans lesquels l'indice de réfraction dépend de la polarisation et de la direction de l'onde incidente. Cela crée des directions différentes de propagation dans le milieu selon la polarisation de l'onde. On parle alors d'indice ou de direction ordinaire et extraordinaire.
Une exemple de biréfringence

Un texte vu à travers un cristal de calcite. La biréfringence fait apparaître le texte en double.
Crédit :
Adrian Pingstone
La polarisation par biréfringence

Un texte vu à travers du calcite et un polariseur. Selon le sens du polariseur, on laisse passer le rayon ordinaire ou extraordinaire, polarisés perpendiculairement.
Crédit :
Aldoaldoz, CC-BY-SA
Les deux rayons ordinaires et extraordinaires sont polarisés différemment, souvent dans des directions perpendiculaires. Cette propriété peut-être utilisée pour créer des analyseurs de polarisation.
 Les polaroid
Les polaroid
Certains matériaux ne sont pas biréfringents, mais sont tout de même polarisants. C'est le cas des polaroid, qui sont des filtres dont les molécules sont toutes orientées dans la même direction. La lumière polarisée perpendiculairement aux molécules est transmise, l'autre composante étant bloquée.
 Lors de la traversée d'une interface
Lors de la traversée d'une interface
Lorsqu'une onde électromagnétique arrive à une interface, par exemple entre l'air et du verre, une partie de l'onde est transmise dans le verre et une partie est réfléchie. Selon l'indice de réfraction des deux milieux, l'angle d'incidence de l'onde et sa polarisation, les composantes transmises et réfléchies varient. Observer les variations de la polarisation après transmission ou réflexion par l'interface peut ainsi donner de précieuses informations sur le milieu.
En particulier, il existe un angle, appelé angle de Brewster où seule la composante de polarisation parallèle à l'interface est réfléchie.
La polarisation par reflexion

Une fenêtre vue sans (à gauche) et avec (à droite) un polariseur. À droite, la réflexion est supprimée par un polariseur bloquant la composante verticale de la polarisation.
Crédit :
Tchannon, CC-BY-SA
Applications à la planétologie
Auteur: Loïc Rossi
La polarimétrie dans le système solaire
Planètes
Pour la planétologie, la polarisation par diffusion atmosphérique est un phénomène intéressant, car observée
sur une autre planète, elle apporte des informations sur les composants atmosphériques, les nuages, et éventuellement des cristaux
de glace ou des poussières. Ainsi, la composition des nuages de Vénus a pu être déterminée grâce à des mesures de polarimétrie comparées à des modèles de diffusion de Mie et Rayleigh..
L'étude des planètes sans (ou avec une fine) atmosphère est plus complexe car la polarisation provient alors essentiellement de la diffusion par la surface. Les modèles de diffusion par des surfaces irrégulières comme du régolithe sont délicats à mettre en œuvre. Cependant, les courbes de polarisation de corps comme Mars ou la Lune peuvent être comparés à des mesures en laboratoire menées sur des analogues. Ainsi pour la Lune ou Mars, la comparaison avec des analogues de roches de type volcaniques et silicates donne des résultats en accord avec les mesures in-situ.
Astéroïdes
L'étude des astéroïdes par polarimétrie complète avantageusement d'autres méthodes telles que la spectroscopie. Il a ainsi été constaté que les courbes de phase polarimétriques des astéroïdes permettent de déterminer leur albédo, ce qui n'est pas toujours aisé par d'autres techniques..
À l'instar des formes de vie, il existe pour les astéroïdes une taxonomie où les objets sont distingués par leur type spectral correspondant à leurs propriétés de surface et à leur composition. L'étude par polarimétrie a mis en évidence que certains astéroïdes qui appartiennent à une même classe spectrale présentent des signatures polarimétriques distinctes, permettant d'affiner les classifications.
Comètes
Les comètes sont aussi étudiées en polarimétrie, notamment afin de caractériser les grains de poussière cométaire (taille, forme et composition). Des variations de la polarisation selon la distance au noyau mettent en évidence des changements dans le type de grains selon qu'ils soient dans la coma ou dans la queue. De même, des variations de polarisation après la rupture d'une comète peuvent indiquer des changements dans les propriétés des grains après un tel évènement.
Applications à l'exoplanétologie
Détection
L'exoplanétologie pourrait aussi tirer des informations de la polarisation. En effet, la lumière d'une étoile est généralement non polarisée, tandis que la lumière réfléchie et diffusée par l'atmosphère de la planète le sera par la surface et par l'atmosphère de la planète.
Ainsi une planète qui serait noyée dans la lumière de son étoile hôte pourrait être invisible en photométrie, mais détectable en polarisation ! Mieux, selon la polarisation mesurée, on pourrait déterminer si la planète possède ou non des nuages et caractériser ces derniers.
Caractérisation
La polarisation peut aussi donner les informations sur la planète, comme pour le système solaire. Ainsi détecter des structures polarimétriques comme des gloires ou des arcs-en-ciel pourraient indiquer la présence de nuages d'eau. À l'inverse, une polarisation de type Rayleigh pourrait indiquer que la planète ne possède pas de nuages.
Outre les paramètres de l'atmosphère ou de la surface, la polarisation peut permettre de mesurer certains paramètres orbitaux de la planète. En effet, la polarisation étant sensible à une rotation du plan de diffusion, la variation de la polarisation avec la rotation de la planète autour de son étoile peut être reliée à une inclinaison du plan orbital et/ou à une excentricité de l'orbite.
Disque protoplanétaires
Les disques protoplanétaires peuvent aussi être étudiés par polarimétrie. La lumière de l'étoile au centre du disque est non polarisée, mais les grains du disque autour diffusent la lumière et génèrent ainsi beaucoup de polarisation. Un instrument sensible à la polarisation peut ainsi mieux voir le disque qu'en lumière normale et peut donc l'étudier plus en détail.
L'étoile HR4796A
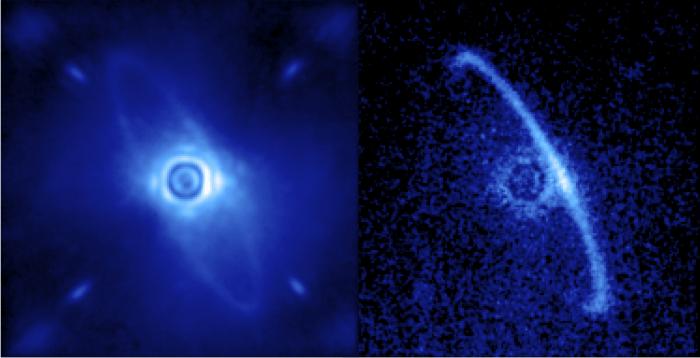
L'étoile HR4796A observée par le Gemini Planet Imager. À gauche, l'image en intensité et à droite la même cible en lumière polarisée. La lumière de l'étoile est non polarisée tandis que le disque de poussières présent autour de celle-ci polarise fortement la lumière. L'observation en lumière polarisée permet ainsi de mieux distinguer le disque de son étoile.
Crédit :
Gemini Planet Imager; Processing by Marshall Perrin, Space Telescope Science Institute.
Pour de tels disques, on peut ainsi étudier les grains qui les composent, mais aussi identifier leur orientation et d'éventuelles structures internes. Ce genre d'observations permet ainsi de mieux contraindre les modèles de formation planétaire.
Comprendre
Auteur: Loïc Rossi
Réflexion et transmission
Auteur: Loïc Rossi
Interfaces entre deux milieux
Supposons une interface entre deux milieux d'indices respectifs 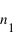 et
et 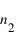 . Un rayon arrive sur cette interface avec un angle
. Un rayon arrive sur cette interface avec un angle 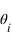 par rapport à la normale à l'interface. Une partie est réfléchie avec un angle
par rapport à la normale à l'interface. Une partie est réfléchie avec un angle 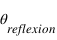 et une partie est réfractée avec un angle
et une partie est réfractée avec un angle 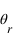 .
.
À l'interface entre deux milieux
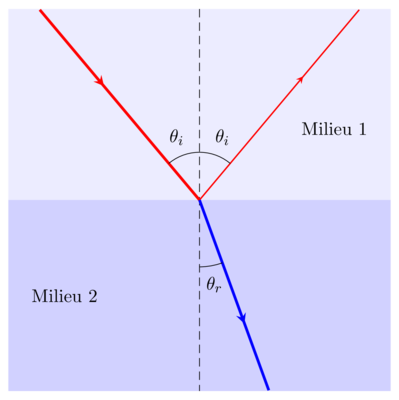
Illustration d'une interface entre deux milieux d'indices de réfraction
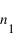
et
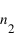
respectivement. Un rayon arrive avec un angle
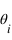
à l'interface. Il est en partie réfléchi avec un angle
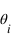
et en partie réfracté avec un angle
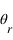
.
Crédit :
Loïc Rossi CC-BY-SA
Polarisation perpendiculaire au plan d'incidence
Si on suppose que l'onde incidente est polarisée perpendiculairement au plan d'incidence, on a : 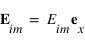 .
.
Cas où E est perpendiculaire
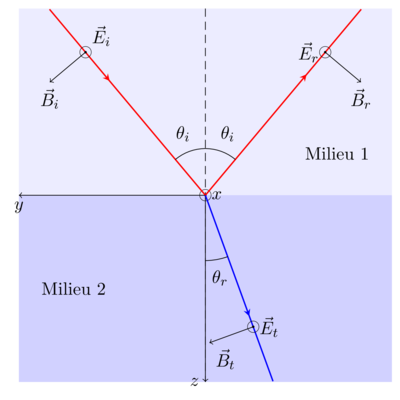
Un rayon incident arrive avec un angle
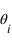
avec la normale à une interface. Le rayon incident est polarisé perpendiculairement au plan d'incidence.
Crédit :
Loïc Rossi CC-BY-SA
À l'interface entre les deux milieux, et à partir des lois de Maxwell, on a des relations de continuité entre les différentes composantes des champs électrique et magnétique. Ainsi, les composantes tangentielles du champ électrique se conservent. Les champs électriques étant déjà parallèles à l'interface, on a donc : 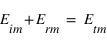 (1).
(1).
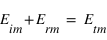 (1)
(1)
En ce qui concerne le champ magnétique, ce sont les composantes normales qui sont conservées. Comme 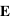 est perpendiculaire à
est perpendiculaire à 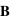 , les champs magnétiques incidents, transmis et réfléchis sont dans le plan d'incidence et on a, par projection sur l'axe (Oz) :
, les champs magnétiques incidents, transmis et réfléchis sont dans le plan d'incidence et on a, par projection sur l'axe (Oz) :
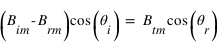 (2) où
(2) où 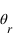 est l'angle de réfraction.
est l'angle de réfraction.
Par ailleurs, l'équation de Maxwell-Faraday permet d'établir que 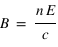 . On peut alors écrire :
. On peut alors écrire :
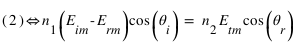 .
.
En remplaçant 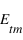 par son expression en (1), on peut écrire :
par son expression en (1), on peut écrire : 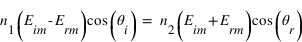 . Ce qui devient, après quelques arrangements :
. Ce qui devient, après quelques arrangements :
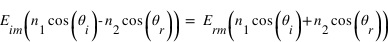
et donne finalement les coefficients de réflexion et de transmission, dits coefficients de Fresnel :
Polarisation parallèle au plan d'incidence
Si on suppose maintenant que la polarisation du champ 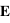 est dans le plan d'incidence, on aura :
est dans le plan d'incidence, on aura : 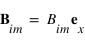 .
.
Cas où E est parallèle
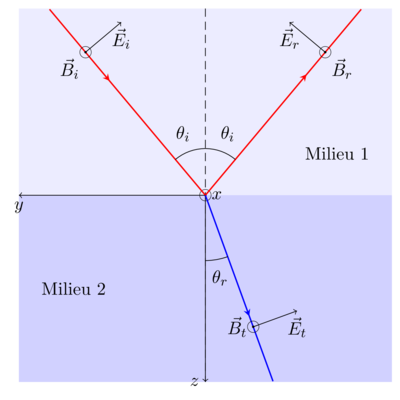
Un rayon incident arrive avec un angle
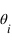
avec la normale à une interface. Le rayon incident est polarisé parallèlement au plan d'incidence.
Crédit :
Loïc Rossi CC-BY-SA
Pour le champ magnétique, on a la relation de continuité 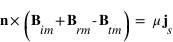 liant les composantes tangentielles du champ avec le courant surfacique parcourant l'interface. Ici, ce courant est nul, ce qui nous permet d'écrire que :
liant les composantes tangentielles du champ avec le courant surfacique parcourant l'interface. Ici, ce courant est nul, ce qui nous permet d'écrire que :
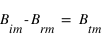 (1)
(1)
ainsi que 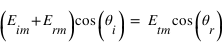 (2)
(2)
En utilisant à nouveau la relation 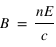 , on peut écrire :
, on peut écrire :
L'équation (2) devient quant à elle, avec la même astuce :
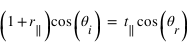 (4)
(4)
En utilisant les expressions (3) et (4) on retrouve les deux autres coefficients de Fresnel :
Les coefficients de Fresnel mettent à jour un cas particulier. En effet si 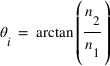 , on a
, on a 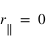 ! L'onde polarisée parallèlement au plan d'incidence (perpendiculairement à l'interface) est totalement transmise ! Cet angle particulier porte le nom d'angle de Brewster d'après David Brewster qui l'a mis en évidence le premier.
! L'onde polarisée parallèlement au plan d'incidence (perpendiculairement à l'interface) est totalement transmise ! Cet angle particulier porte le nom d'angle de Brewster d'après David Brewster qui l'a mis en évidence le premier.
Coefficients de réflexion et de transmission
 Coefficients de réflexion et transmission
Coefficients de réflexion et transmission
Les coefficients calculés ci-avant sont des coefficients de réflexion et de transmission en amplitude des ondes. Or on mesure généralement l'intensité de la lumière. On va donc utiliser des considérations énergétiques (conservation de l'énergie notamment) pour définir les coefficients de réflexion et transmission à l'interface.
Les deux cas étudiés précédements sont applicables au cas général où la lumière n'est pas polarisée. En effet, on peut considérer la lumière naturelle comme ayant une composante polarisée parallèlement au plan d'incidence et une composante polarisée perpendiculairement au plan d'incidence.
C'est l'étude de la lumière transmise ou réfléchie par un corps dans différentes polarisations qui va fournir des informations sur le milieu, car les coefficients de Fresnel dépendent de la géométrie, mais aussi des caractéristiques des milieux, via 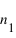 et
et 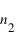 .
.
Usages
Emissivité
On peut s'intéresser à la polarisation du rayonnement thermique issu d'un corps. Normalement le rayonnement thermique n'est pas polarisé, mais la traversée du milieu (le sol par exemple) va le polariser et l'on va pouvoir mesurer cet effet. C'est ce qui est utilisé par exemple par la sonde Cassini qui étudie Titan.
On va donc s'intéresser à la transmission du corps en fonction de la géométrie d'observation et de son indice de réfraction (ou sa permittivité électrique). On parlera alors d'emissivité du corps.
v
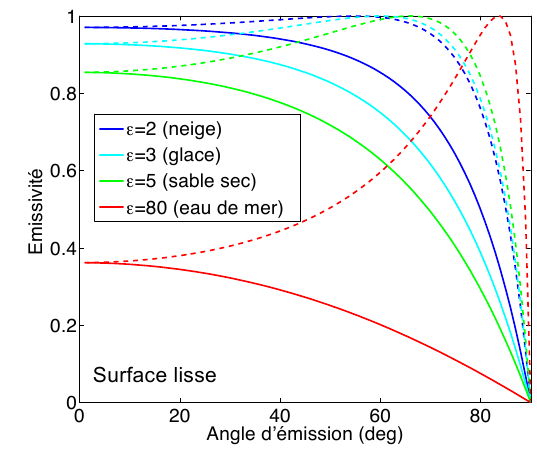
Figure montrant l'emissivité en fonction de l'angle d'émission pour différentes permittivités. Les courbes pleines correspondent à la polarisation perpendiculaire et les courbes en tirets correspondent à la polarisation parallèle. On voit ainsi que l'emissivité diminue avec la hausse de la permittivité.
Crédit :
Figure produite par Alice Le Gall (LATMOS)
Carte d'emissivité du pole nord de Titan
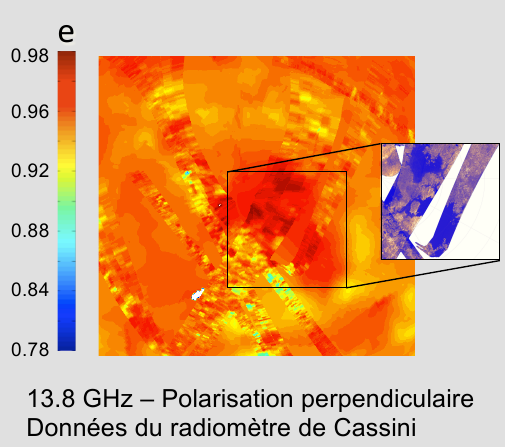
Carte d'émissivité du pôle de Titan obtenue par le radiomètre de Cassini en polarisation perpendiculaire. L'emissivité mesurée a permis d'établir que la permitivité des lacs de Titan est entre 1,6 et 1,9 : ce sont des lacs d'hydrocarbures !
On mesure généralement le degré de polarisation 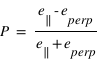 où
où 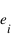 est l'émissivité en polarisation parallèle ou perpendiculaire au plan de diffusion.
est l'émissivité en polarisation parallèle ou perpendiculaire au plan de diffusion.
Reflexion
On peut également utiliser cette méthode de façon active en envoyant une onde polarisée sur une surface avec un radar et en étudiant la réflexion de cette onde sur le corps étudié. (Donner Exemple)
La polarisation par diffusion
Auteur: Loïc Rossi
Les différents régimes
La diffusion Rayleigh
La diffusion Rayleigh se produit dans le cas de diffuseurs petits par rapport à la longueur (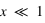 ), ayant un indice de réfraction proche de l'unité ou satisfaisant
), ayant un indice de réfraction proche de l'unité ou satisfaisant 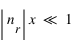 .
.
La diffusion Rayleigh
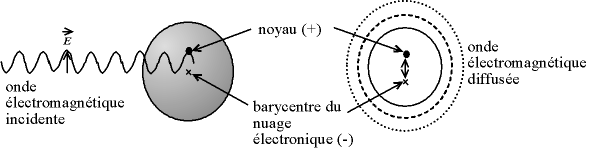
Une onde électromagnétique incidente fait osciller le nuage électroniques des atomes. Le dipôle électrostatique généré rayonne une onde électromagnétique de même longueur d'onde : la diffusion Rayleigh.
Crédit :
Christophe Dang Ngoc Chan, CC-BY-SA
Lorsqu'un onde électromagnétique rencontre le diffuseur, elle génère un dipôle électrostatique de moment 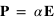 , où
, où 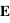 est le champ électrique incident et α la polarisabilité du diffusant. Ce dipôle va rayonner une onde de même fréquence dans toutes les directions. Cependant, l'intensité et la polarisation de l'onde rayonnée vont dépendre de l'angle de diffusion.
est le champ électrique incident et α la polarisabilité du diffusant. Ce dipôle va rayonner une onde de même fréquence dans toutes les directions. Cependant, l'intensité et la polarisation de l'onde rayonnée vont dépendre de l'angle de diffusion.
On peut montrer que la fonction de phase est 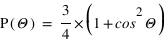 , où Θ est l'angle de diffusion.
, où Θ est l'angle de diffusion.
En ce qui concerne la polarisation, on va considérer que la lumière incidente est non polarisée (ce qui est vrai pour la lumière solaire) et considérer les directions parallèle et perpendiculaire au plan de diffusion, que l'on va noter avec les indices 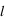 et
et 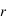 respectivement. La composante diffusée polarisée perpendiculairement au plan de diffusion,
respectivement. La composante diffusée polarisée perpendiculairement au plan de diffusion, 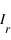 ne dépend pas de Θ, tandis que
ne dépend pas de Θ, tandis que 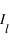 évolue en
évolue en 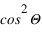 . Dès lors, si on s'intéresse au degré linéaire de polarisation, on aura :
. Dès lors, si on s'intéresse au degré linéaire de polarisation, on aura :
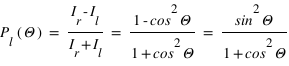
Ceci rend compte du maximum de polarisation observé par diffusion Rayleigh pour un angle de phase de 90°.
Exercices
Auteur: Loïc Rossi
Exercices
Exercices
Auteur: Loïc Rossi
 Premières interprétations
Premières interprétations
On observe les vecteurs de Stokes suivants (mesurés tels que le plan de diffusion est horizontal) :
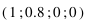
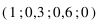
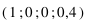
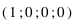
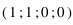
Question 1)
Lequel de ces vecteurs correspond à une lumière totalement polarisée ? Même question pour une lumière non-polarisée.
Question 2)
Lequel (lesquels) de ces vecteurs décrit une lumière circulairement polarisée ?
Question 3)
Quels sont les vecteurs de lumière linéairement polarisés ?
Question 4)
À quels vecteurs pourrait-on associer de la lumière diffusée selon le régime de Rayleigh ?
La diffusion Rayleigh polarise la lumière perpendiculairement au plan de diffusion.
Question 5)
Quel est le degré de polarisation linéaire de ces vecteurs ? Même question avec le degré total de polarisation.
Mini-projet
Auteur: Loïc Rossi
Mini-projet : les gloires de Vénus
Auteur: Loïc Rossi
 Questions introductives
Questions introductives
Difficulté : ☆
On se propose dans ce projet d'étudier les nuages de Vénus à l'aide de la polarimétrie. On va pour cela utiliser des mesures prises par l'instrument SPICAV-IR, à bord de la sonde européenne Venus Express.
Question 1)
Dans une atmosphère comme celle de Vénus avec des nuages et du gaz, quels sont les processus de diffusion que l'on doit considérer ?
Question 2)
SPICAV-IR observe Vénus dans la fin du domaine visible et l'infrarouge proche. Dans ce cas, lequel des processus évoqués ci-dessus peuvent être négligés ?
Question 4)
SPICAV-IR peut-il mesurer les éléments de Stokes U et V ?
Mini-projet : les gloires de Vénus
Auteur: Loïc Rossi
 Ajustement d'une gloire
Ajustement d'une gloire
On va ici étudier une gloire observée en polarisation par SPICAV-IR. Dans ce type d'observation, la sonde regarde un endroit fixe sur Vénus. Ainsi seul l'angle d'émission varie tandis que l'angle solaire zénithal reste constant.
L'application (disponible ici) présente l'observation SPICAV-IR pour trois longueurs d'onde (1,1 ; 1,274 et 1,553 μm) en rouge. Pour chacune de ces longueurs d'onde l'application permet de calculer un modèle de polarisation. Ce modèle simplifié dépend du rayon efficace des particules des nuages ainsi que de leur indice de réfraction. L'indice de réfraction dépendant de la longueur d'onde, il est ajustable séparément pour chaque longueur d'onde.
Question 1)
En « jouant » avec les paramètres du modèle, tentez de trouver des valeurs qui permettent d'ajuster l'observation à toutes les longueurs d'onde.
Question 2)
Quelle est l'évolution générale des indices de réfraction ? En vous appuyant sur les tables d'indices suivants, quels types de composés peut-on exclure pour la composition des nuages ? Quels composés sont possibles ?
Indices de réfraction de certains composés
| Longueur d'onde (µm) | Indices de réfraction approximatifs |
|---|
| Composé | Eau | Acide sulfurique | Poussières volcaniques |
| 1,1 | 1,326 | 1,42 | 1,50 |
| 1,274 | 1,323 | 1,41 | 1,50 |
| 1,553 | 1,318 | 1,40 | 1,49 |
-------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------
ACCES AU PLAN DES CHAPITRES
Réponses aux QCM
pages_polarisation-exos2/exos1.html
QCM
'Une mise en jambes'
- Question 1
Solution : réponse 2)
(
Au coucher du Soleil, la lumière doit traverser plus d'air avant de nous atteindre. La lumière bleue étant plus diffusée, plus de lumière rouge nous atteint.
)
- Question 2
Solution : réponse 1)
(
La lumière réfléchie sur la chaussée est fortement polarisée paralèllement au sol. Porter des verres polarisants peut permettre d'éliminer cette composante, et d'éviter les reflets gênants.
)
Réponses aux exercices
pages_polarisation/exos2.html
Exercice
'Premières interprétations'
pages_polarisation/projet1.html
Exercice
'Questions introductives'
- Question 1
Solution :
Il faut ici considérer la diffusion de Rayleigh, causée par le gaz. Il faut aussi considérer la diffusion de Mie pour les aérosols sphériques (les gouttes) dans l'atmosphère.
- Question 2
Solution :
La section efficace de la diffusion de Rayleigh dépend de la longueur d'onde de la lumière en 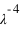 . De fait la diffusion de Rayleigh aura surtout un effet à des longueurs d'onde courtes, et donc plutôt en UV et dans le blue. SPICAV-IR observant dans le rouge et l'IR, il sera peu sensible à cette diffusion, laquelle pourra être ignorée, surtout lorsqu'il va s'agir de comparer les opacités du gaz et des nuages.
. De fait la diffusion de Rayleigh aura surtout un effet à des longueurs d'onde courtes, et donc plutôt en UV et dans le blue. SPICAV-IR observant dans le rouge et l'IR, il sera peu sensible à cette diffusion, laquelle pourra être ignorée, surtout lorsqu'il va s'agir de comparer les opacités du gaz et des nuages.
- Question 3
Solution :
Le degré de polarisation linéaire est défini par 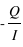 , ou encore
, ou encore 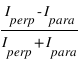 , on a donc :
, on a donc : 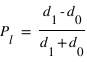
- Question 4
Solution :
Non, car les détecteurs ne mesurent que les composantes parallèles et perpendiculaires de la polarisation. Il ne peut donc mesurer que I et Q.
 Objectif
Objectif Pré-requis
Pré-requis Illustrations et figures
Illustrations et figures


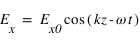
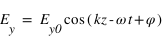 , où
, où 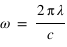 est la pulsation de l'onde électromagnétique;
est la pulsation de l'onde électromagnétique; 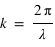 le nombre d'onde et
le nombre d'onde et 

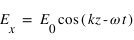
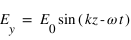 , où
, où 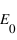 est l'amplitude commune des deux composantes du champ électrique. La phase vaut alors
est l'amplitude commune des deux composantes du champ électrique. La phase vaut alors 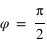 .
.


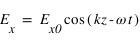
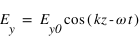 , avec
, avec 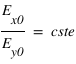 et
et 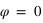 .
.



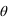 l'angle entre la direction du filtre et la direction de polarisation de l'onde incidente et
l'angle entre la direction du filtre et la direction de polarisation de l'onde incidente et 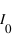 son intensité, on a après le polariseur une intensité
son intensité, on a après le polariseur une intensité 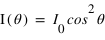 , c'est la Loi de Malus. De fait, on retrouve qu'un polariseur dont la direction de polarisation est perpendiculaire à celle de la lumière incidente, il ne transmettra rien. De même, deux polariseurs de directions perpendiculaires (on dit qu'ils sont croisés) ne laissent pas passer la lumière: celle-ci est polarisée dans une direction par le premier polariseur, puis bloquée par le second, de direction perpendiculaire. Dans le cas d'une source non polarisée
, c'est la Loi de Malus. De fait, on retrouve qu'un polariseur dont la direction de polarisation est perpendiculaire à celle de la lumière incidente, il ne transmettra rien. De même, deux polariseurs de directions perpendiculaires (on dit qu'ils sont croisés) ne laissent pas passer la lumière: celle-ci est polarisée dans une direction par le premier polariseur, puis bloquée par le second, de direction perpendiculaire. Dans le cas d'une source non polarisée 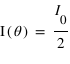 .
.

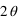 . L'utilisation principale qui en est faite est de changer la direction de polarisation linéaire. Une onde polarisée avec un angle
. L'utilisation principale qui en est faite est de changer la direction de polarisation linéaire. Une onde polarisée avec un angle 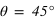 par rapport à l'axe rapide aura en sortie un angle
par rapport à l'axe rapide aura en sortie un angle 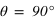 avec l'axe rapide : les directions incidentes et émergentes sont donc croisées !
avec l'axe rapide : les directions incidentes et émergentes sont donc croisées !

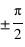 (ou un quart de longueur d'onde). Une telle lame permet de transformer une polarisation linéaire en une polarisation elliptique ou circulaire, et inversement. En effet dans le cas linéaire, les deux composantes du champ électrique, parallèle et perpendiculaire à l'axe rapide sont de la forme
(ou un quart de longueur d'onde). Une telle lame permet de transformer une polarisation linéaire en une polarisation elliptique ou circulaire, et inversement. En effet dans le cas linéaire, les deux composantes du champ électrique, parallèle et perpendiculaire à l'axe rapide sont de la forme 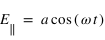 et
et 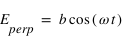 . Si on introduit un déphasage de
. Si on introduit un déphasage de 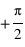 , les deux composantes deviendont
, les deux composantes deviendont 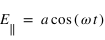 et
et 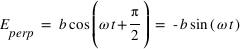 , le vecteur du champ électrique va donc décrire une ellipse !
, le vecteur du champ électrique va donc décrire une ellipse !

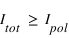 où
où 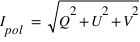 . Le degré de polarisation, décrivant la proportion de la lumière qui est polarisée est donc
. Le degré de polarisation, décrivant la proportion de la lumière qui est polarisée est donc 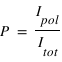 . Si on note
. Si on note 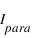 la polarisation parallèle au plan de référence et
la polarisation parallèle au plan de référence et 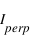 la composante polarisée perpendiculairement au plan de référence, on a
la composante polarisée perpendiculairement au plan de référence, on a 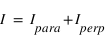 .
.
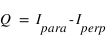
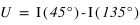
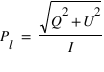 . Si on est dans le cas où
. Si on est dans le cas où 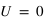 ,alors
,alors 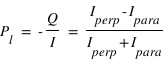 .
.
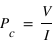 .
.








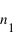 et
et 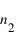 . Un rayon arrive sur cette interface avec un angle
. Un rayon arrive sur cette interface avec un angle 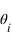 par rapport à la normale à l'interface. Une partie est réfléchie avec un angle
par rapport à la normale à l'interface. Une partie est réfléchie avec un angle 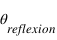 et une partie est réfractée avec un angle
et une partie est réfractée avec un angle 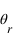 .
.

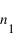 et
et 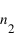 respectivement. Un rayon arrive avec un angle
respectivement. Un rayon arrive avec un angle 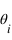 à l'interface. Il est en partie réfléchi avec un angle
à l'interface. Il est en partie réfléchi avec un angle 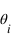 et en partie réfracté avec un angle
et en partie réfracté avec un angle 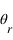 .
.
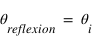
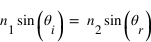
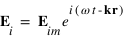 où
où 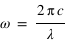 , et où
, et où 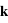 et
et 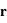 sont le vecteur d'onde et le vecteur position respectivement.
sont le vecteur d'onde et le vecteur position respectivement. 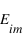 est le module du vecteur de champ électrique incident.
est le module du vecteur de champ électrique incident.
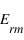 le module du champ électrique réfléchi par l'interface et
le module du champ électrique réfléchi par l'interface et 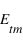 le module du champ transmis par l'interface. On va définir deux coefficients : le coefficient de transmission
le module du champ transmis par l'interface. On va définir deux coefficients : le coefficient de transmission 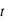 et le coefficient de réflexion
et le coefficient de réflexion 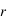 , tels que :
, tels que :
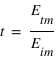
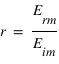
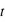 et de
et de 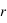 on va s'intéresser à deux cas de polarisation de l'onde incidente.
on va s'intéresser à deux cas de polarisation de l'onde incidente.
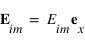 .
.

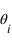 avec la normale à une interface. Le rayon incident est polarisé perpendiculairement au plan d'incidence.
avec la normale à une interface. Le rayon incident est polarisé perpendiculairement au plan d'incidence.
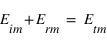 (1).
(1).
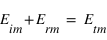 (1)
(1)
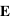 est perpendiculaire à
est perpendiculaire à 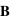 , les champs magnétiques incidents, transmis et réfléchis sont dans le plan d'incidence et on a, par projection sur l'axe (Oz) :
, les champs magnétiques incidents, transmis et réfléchis sont dans le plan d'incidence et on a, par projection sur l'axe (Oz) :
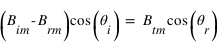 (2) où
(2) où 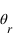 est l'angle de réfraction.
est l'angle de réfraction.
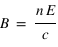 . On peut alors écrire :
. On peut alors écrire :
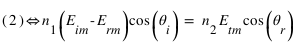 .
.
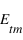 par son expression en (1), on peut écrire :
par son expression en (1), on peut écrire : 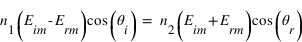 . Ce qui devient, après quelques arrangements :
. Ce qui devient, après quelques arrangements :
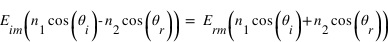
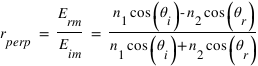
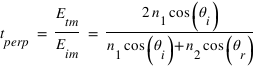
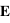 est dans le plan d'incidence, on aura :
est dans le plan d'incidence, on aura : 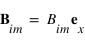 .
.

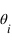 avec la normale à une interface. Le rayon incident est polarisé parallèlement au plan d'incidence.
avec la normale à une interface. Le rayon incident est polarisé parallèlement au plan d'incidence.
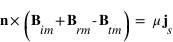 liant les composantes tangentielles du champ avec le courant surfacique parcourant l'interface. Ici, ce courant est nul, ce qui nous permet d'écrire que :
liant les composantes tangentielles du champ avec le courant surfacique parcourant l'interface. Ici, ce courant est nul, ce qui nous permet d'écrire que :
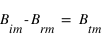 (1)
(1)
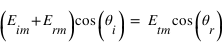 (2)
(2)
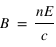 , on peut écrire :
, on peut écrire :
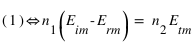 ,
, 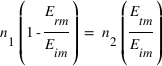
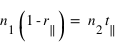 (3)
(3)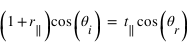 (4)
(4)
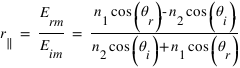
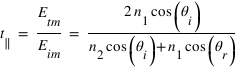
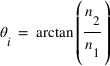 , on a
, on a 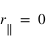 ! L'onde polarisée parallèlement au plan d'incidence (perpendiculairement à l'interface) est totalement transmise ! Cet angle particulier porte le nom d'angle de Brewster d'après David Brewster qui l'a mis en évidence le premier.
! L'onde polarisée parallèlement au plan d'incidence (perpendiculairement à l'interface) est totalement transmise ! Cet angle particulier porte le nom d'angle de Brewster d'après David Brewster qui l'a mis en évidence le premier.
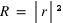
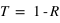
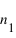 et
et 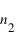 .
.


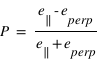 où
où 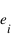 est l'émissivité en polarisation parallèle ou perpendiculaire au plan de diffusion.
est l'émissivité en polarisation parallèle ou perpendiculaire au plan de diffusion.
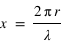 , où
, où 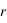 est le rayon du diffusant et
est le rayon du diffusant et 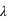 la longueur d'onde du photon incident. Le paramètre de taille permet de distinguer le régime de Rayleigh et celui de Mie :
la longueur d'onde du photon incident. Le paramètre de taille permet de distinguer le régime de Rayleigh et celui de Mie :
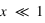 , on est dans le régime de Rayleigh, où les particules sont petites devant la longueur d'onde ;
, on est dans le régime de Rayleigh, où les particules sont petites devant la longueur d'onde ;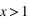 , on est dans le régime de Mie, avec des effets particuliers, notamment d'interférences ;
, on est dans le régime de Mie, avec des effets particuliers, notamment d'interférences ;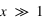 , on rentre dans l'approximation de l'optique géométrique. Certains effets de la diffusion de Mie ne sont plus expliqués simplement par l'optique géométrique.
, on rentre dans l'approximation de l'optique géométrique. Certains effets de la diffusion de Mie ne sont plus expliqués simplement par l'optique géométrique. 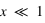 ), ayant un indice de réfraction proche de l'unité ou satisfaisant
), ayant un indice de réfraction proche de l'unité ou satisfaisant 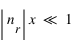 .
.

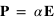 , où
, où 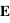 est le champ électrique incident et
est le champ électrique incident et 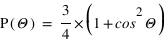 , où
, où 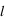 et
et 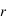 respectivement. La composante diffusée polarisée perpendiculairement au plan de diffusion,
respectivement. La composante diffusée polarisée perpendiculairement au plan de diffusion, 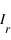 ne dépend pas de
ne dépend pas de 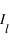 évolue en
évolue en 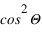 . Dès lors, si on s'intéresse au degré linéaire de polarisation, on aura :
. Dès lors, si on s'intéresse au degré linéaire de polarisation, on aura :
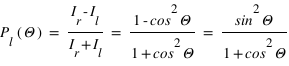
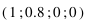
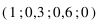
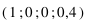
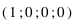
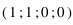
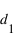 ) mesure
) mesure 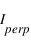 et le détecteur 0 (
et le détecteur 0 (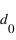 ) mesure
) mesure 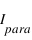 . Quelle va être l'expression du degré de polarisation linéaire ?
. Quelle va être l'expression du degré de polarisation linéaire ?
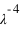 . De fait la diffusion de Rayleigh aura surtout un effet à des longueurs d'onde courtes, et donc plutôt en UV et dans le blue. SPICAV-IR observant dans le rouge et l'IR, il sera peu sensible à cette diffusion, laquelle pourra être ignorée, surtout lorsqu'il va s'agir de comparer les opacités du gaz et des nuages.
. De fait la diffusion de Rayleigh aura surtout un effet à des longueurs d'onde courtes, et donc plutôt en UV et dans le blue. SPICAV-IR observant dans le rouge et l'IR, il sera peu sensible à cette diffusion, laquelle pourra être ignorée, surtout lorsqu'il va s'agir de comparer les opacités du gaz et des nuages.
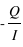 , ou encore
, ou encore 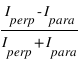 , on a donc :
, on a donc :