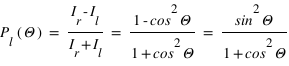Le paramètre de taille
Le paramètre de taille
Pour étudier les processus de diffusion tels que la diffusion de Rayleigh ou de Mie, on va utiliser le paramètre de taille 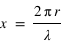 , où
, où 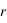 est le rayon du diffusant et
est le rayon du diffusant et 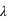 la longueur d'onde du photon incident. Le paramètre de taille permet de distinguer le régime de Rayleigh et celui de Mie :
la longueur d'onde du photon incident. Le paramètre de taille permet de distinguer le régime de Rayleigh et celui de Mie :
- Pour
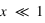 , on est dans le régime de Rayleigh, où les particules sont petites devant la longueur d'onde ;
, on est dans le régime de Rayleigh, où les particules sont petites devant la longueur d'onde ; - pour
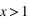 , on est dans le régime de Mie, avec des effets particuliers, notamment d'interférences ;
, on est dans le régime de Mie, avec des effets particuliers, notamment d'interférences ; - pour
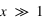 , on rentre dans l'approximation de l'optique géométrique. Certains effets de la diffusion de Mie ne sont plus expliqués simplement par l'optique géométrique.
, on rentre dans l'approximation de l'optique géométrique. Certains effets de la diffusion de Mie ne sont plus expliqués simplement par l'optique géométrique.
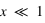 ), ayant un indice de réfraction proche de l'unité ou satisfaisant
), ayant un indice de réfraction proche de l'unité ou satisfaisant 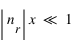 .
.
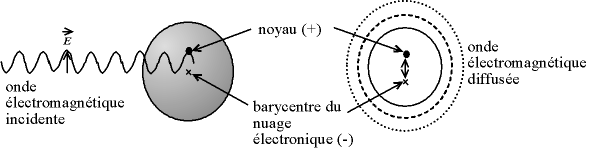
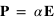 , où
, où 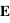 est le champ électrique incident et
est le champ électrique incident et 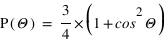 , où
, où 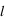 et
et 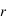 respectivement. La composante diffusée polarisée perpendiculairement au plan de diffusion,
respectivement. La composante diffusée polarisée perpendiculairement au plan de diffusion, 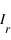 ne dépend pas de
ne dépend pas de 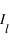 évolue en
évolue en 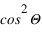 . Dès lors, si on s'intéresse au degré linéaire de polarisation, on aura :
. Dès lors, si on s'intéresse au degré linéaire de polarisation, on aura :