L'interaction entre le rayonnement (ondes du champ électromagnétique) et la matière (chargée au niveau microscopique : électrons, noyaux atomiques) se caractérise par trois types de processus radiatifs : l'absorption, l'émission et la diffusion.
Émission
Un processus d'émission intervient lorsque la matière cède localement de l'énergie au champ électromagnétique (création d'un photon). Cette émission est qualifiée de thermique lorsque le champ et la matière sont à l'équilibre thermodynamique à une même température 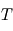 (on peut voir alors leur interaction comme celle d'un gaz de photons perpétuellement absorbés et émis par la matière environnante, et se mettant en équilibre de la sorte). Il existe également des phénomènes d'émission non thermiques (ex: fluorescence, émission laser), mais ils sortent du cadre de ce cours ; certains de ces processus sont vus dans ce chapitre.
(on peut voir alors leur interaction comme celle d'un gaz de photons perpétuellement absorbés et émis par la matière environnante, et se mettant en équilibre de la sorte). Il existe également des phénomènes d'émission non thermiques (ex: fluorescence, émission laser), mais ils sortent du cadre de ce cours ; certains de ces processus sont vus dans ce chapitre.
Illustration d'un processus d'émission spontanée
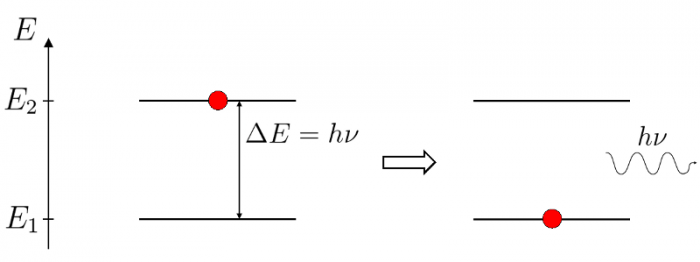
Émission spontanée d'un photon par un système matériel possédant au moins deux niveaux d'énergie. L'énergie totale est conservée dans ce processus.
Absorption
Un processus d'absorption a lieu lorsqu'inversement, le champ électromagnétique cède de l'énergie à la matière environnante (destruction d'un photon).
Illustration d'un processus d'absorption
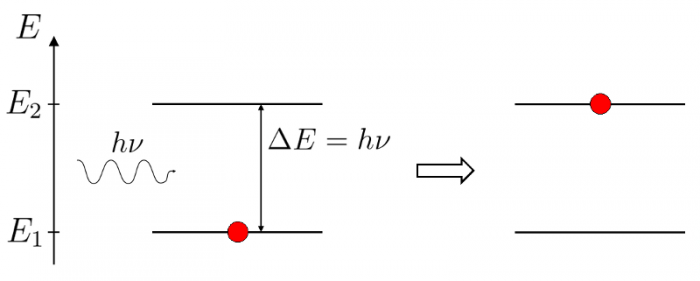
Absorption d'un photon par un système matériel possédant au moins deux niveaux d'énergie. L'énergie totale est conservée dans ce processus.
Diffusion
Lorsque la présence de matière interagit avec l'onde électromagnétique en absorbant et réémettant un photon dans un temps très court, donc sans lui soutirer d'énergie. La réémission s'effectuant dans tout l'espace, il en résulte une déviation des ondes électromagnétiques hors de la direction d'incidence. On appelle ce phénomène diffusion.
Illustration d'un processus de diffusion
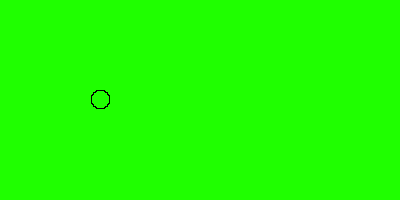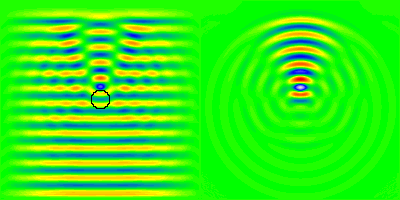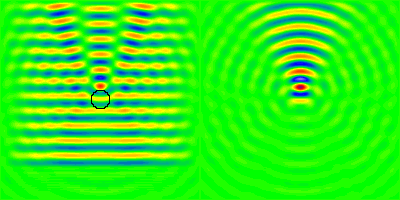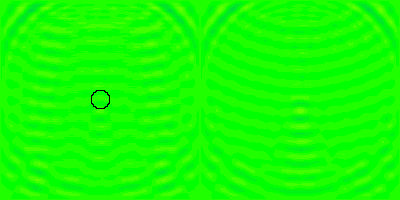
Illustration de la diffusion d'une onde électromagnétique par une sphère diélectrique de rayon comparable à la longueur d'onde et d'indice de réfraction relatif
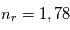
. Le champ électrique total figure à gauche, et la composante diffusée à droite.
Crédit :
R. Hogan (Univ. of Reading)
On regroupe les phénomènes d'absorption et de diffusion sous le nom d'extinction : ces deux phénomènes ont comme point commun de diminuer l'intensité d'un faisceau lumineux dans la direction d'incidence, soit en l'absorbant, soit en en déviant tout ou partie.
Régimes de Rayleigh et de Mie
Le régime de diffusion Rayleigh concerne la diffusion de la lumière par des particules petites devant la longueur d'onde (rayon 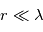 ), ce quelque soit le type d'aérosol (sphérique ou non) : molécules isolées de gaz, micro gouttes, etc.
), ce quelque soit le type d'aérosol (sphérique ou non) : molécules isolées de gaz, micro gouttes, etc.
La théorie de Mie est quant à elle valable pour toutes les valeurs de 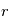 , mais uniquement pour des particules sphériques (gouttes liquides par exemple). Elle tend vers le cas Rayleigh lorsque
, mais uniquement pour des particules sphériques (gouttes liquides par exemple). Elle tend vers le cas Rayleigh lorsque 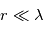 . Pour des particules non sphériques (cristaux, aérosols de Titan, poussières), cette théorie n'est valable qu'en première approximation, et les méthodes utilisées pour aller plus loin sont hors-programme.
. Pour des particules non sphériques (cristaux, aérosols de Titan, poussières), cette théorie n'est valable qu'en première approximation, et les méthodes utilisées pour aller plus loin sont hors-programme.
Section efficace de diffusion
Cette section efficace évolue de façon très différente selon le régime. Dans le régime Rayleigh, la section efficace est une fonction rapidement croissante de la longueur d'onde (une illustration courante étant la diffusion bien plus importante du bleu que de rouge dans l'atmosphère terrestre, donnant sa couleur à notre ciel). En régime de Mie, cette dépendance est bien plus faible, si bien que les diffuseurs apparaissent peu colorés en l'absence d'absorption (sur Terre, les nuages d'eau liquide sont un bon exemple).
Section efficace de diffusion
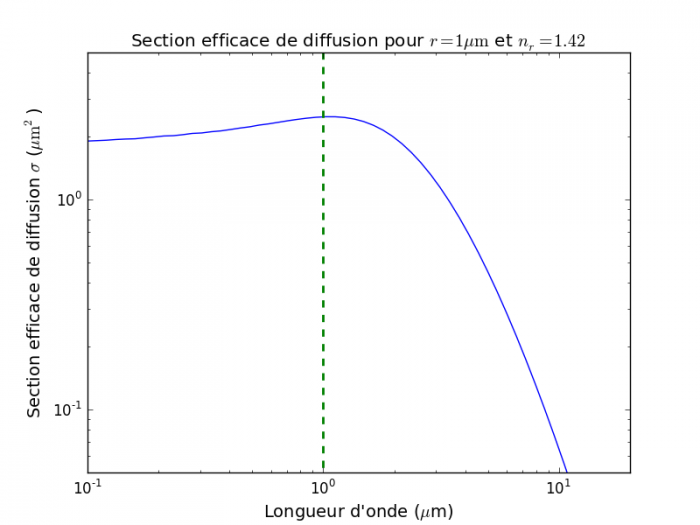
Représentation log-log de la section efficace de diffusion en fonction de la longueur d'onde pour des particules sphériques d'un rayon
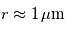
. Aux grandes longueurs d'onde,
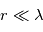
et on se trouve dans le régime
Rayleigh (
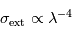
, apparaissant comme une asymptote de pente -4). Pour
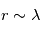
et
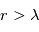
, on se trouve dans le régime de
Mie, où la section efficace est presque indépendante de
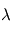
et voisine de la section géométrique des particules.
Crédit :
Loïc Rossi CC-BY-SA
Fonction de phase
La fonction de phase définit la répartition angulaire du rayonnement diffusé. C'est en quelque sorte la probabilité pour un rayon incident d'être diffusé dans une direction donnée.
Fonctions de phase de Rayleigh et de Mie

Figure montrant les indicatrices des différents processus de diffusion. La lumière incidente est supposée aller de gauche à droite. Plus la flèche est longue, plus la diffusion sera importante dans cette direction. À gauche, le régime de Rayleigh avec une diffusion relativement isotrope. Au centre, la diffusion de Mie, qui diffuse fortement vers l'avant. À droite, la diffusion de Mie pour des particules encore plus grandes.
Crédit :
Sharayanan CC-BY-SA
Types de réflexion
Quand du rayonnement parvient à une surface, il peut être réfléchi de plusieurs façons :
- Lambertienne, si les défauts de la surface sont supérieurs à la longueur d'onde du rayonnement incident. La lumière est alors réfléchie dans toutes les directions de façon homogène, on parle alors de surface lambertienne. Un mur blanc est un exemple de surface lambertienne ;
- Spéculaire, si les défauts sont très petits devant la longueur d'onde : la surface agit alors comme un miroir à la longueur d'onde considérée. Une surface liquide (une mer calme) peut agir comme une surface de réflexion spéculaire.
Réflexion diffuse et spéculaire

Photographie de la Terre prise depuis la station spatiale internationale. On distingue nettement la réflexion spéculaire sur la surface de l'océan et celle diffuse due aux nuages ou à la surface des continents.
Spectroscopie
Selon la longueur d'onde, le rayonnement incident sur une surface peut-être réfléchi mais aussi absorbé. On pourra alors étudier la réflectance d'une surface en fonction de la longueur d'onde (la réflectance valant 1 si tout la lumière est réfléchie ; 0 si tout est absorbé.).
L'étude de la réflectance d'une surface en fonction de la longueur d'onde peut être utile pour caractériser celle-ci. Ainsi certains minéraux ont un spectre avec des bandes d'absoption caractéristiques. C'est ce qui permet de caractériser des surfaces comme celles de Mars (pour détecter des minéraux hydratés par exemple), de la Lune ou bien celle d'astéroïdes et de comètes.
Intérêt
Son intérêt principal réside dans l'interprétation des spectres thermiques issus d'un objet (ici une planète et son atmosphère). En effet, sous réserve de certaines hypothèses :
- Absence de diffusion Toute extinction du rayonnement thermique est due à son absorption.
- Absorbant uniformément mélangé et de section efficace indépendante de la pression.
- Atmosphère en équilibre hydrostatique et isotherme en géométrie plan-parallèle (courbure planétaire négligée). L'hypothèse isotherme n'est ici requise que d'un point de vue hydrostatique, pas d'un point de vue radiatif.
La température de brillance correspond alors à la température du milieu situé à une profondeur optique égale à 1 : ![T_B(\lambda) \approx T\left[\tau(\lambda) = 1\right]](../pages_flux-et-spectre/equations_trans-rad/equation41.png) avec
avec 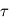 comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :
comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :
- les couches situées à des profondeurs optiques trop grandes devant 1 ne contribuent que faiblement car leur émission est trop atténuée selon la loi de Beer-Lambert.
- l'émission thermique des couches situées à faible profondeur optique est quant à elle peu atténuée, mais hélas trop peu intense pour contribuer significativement au rayonnement reçu (la loi de Kirchhoff impose que les bons émetteurs thermiques doivent aussi être de bons absorbants).
Raies en absorption vs. émission
Nous sommes à présent en mesure d'interpréter pourquoi les raies caractéristiques de certains gaz apparaissent tantôt en absorption, tantôt en émission dans les spectres thermiques observés. En effet, le centre d'une raie spectrale présente une absorption massique plus grande que les ailes de cette même raie. En conséquence, du point de vue d'un observateur extérieur à l'atmosphère, la profondeur optique unité est atteinte à des altitudes plus élevées aux centres des raies que sur leurs ailes. À partir de là, on a les cas de figure suivants :
- Lorsque le profil thermique décroît avec l'altitude (troposphère, mésosphère), les coeurs des raies atteint une profondeur optique de 1 à plus haute altitude, donc sondent un milieu de température plus faible que les ailes : les raies apparaissent alors en absorption.
- Inversement, lorsque le profil thermique croît avec l'altitude (stratosphère), les coeurs des raies sondent un milieu de température plus élevée que les ailes : les raies apparaissent alors en émission.
Raies en absorption ou en émission
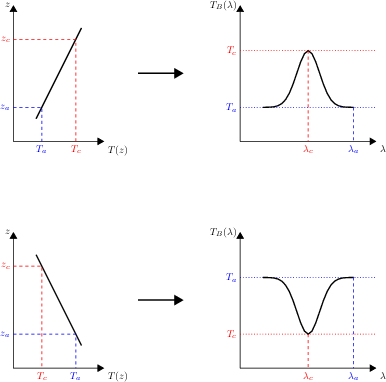
Profils d'une raie spectrale vue en émission (haut) ou en absorption (bas). L'altitude
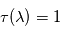
est atteinte plus haut au coeur de la raie (longueur d'onde
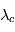
) que dans les ailes lointaines de la raie (longueur d'onde
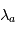
) :
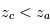
avec
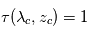
et
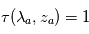
.
Crédit :
Emmanuel Marcq CC-BY-SA
Principe
Lorsque le profil vertical de température est supposé connu dans une atmosphère planétaire (par exemple au moyen de la méthode décrite précédemment), il est possible d'utiliser les raies spectrales de composés identifiés (et bien connus spectroscopiquement) pour en déduire leur profil vertical d'abondance sur une plage d'altitudes donnée.
De façon semi-quantitative et en visée nadir, on peut procéder comme suit : la connaissance du profil thermique 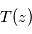 permet, pour chaque longueur d'onde
permet, pour chaque longueur d'onde 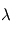 , de retrouver l'altitude
, de retrouver l'altitude 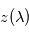 correspondant à la température de brillance observée — en d'autres termes telle que
correspondant à la température de brillance observée — en d'autres termes telle que ![T_B(\lambda) = T\left[z(\lambda)\right]](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation15.png) . Or, on sait que cette altitude correspond à la profondeur optique unité à la longueur d'onde considérée, si bien que l'on a
. Or, on sait que cette altitude correspond à la profondeur optique unité à la longueur d'onde considérée, si bien que l'on a ![\tau \left[ z(\lambda) \right] = \sigma_{\mathrm{abs}}(\lambda) \times N\left[z(\lambda) \right] = 1](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation16.png) où
où 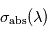 désigne la section efficace d'absorption du composé mesuré (supposée ici indépendante de la pression et de la température) et
désigne la section efficace d'absorption du composé mesuré (supposée ici indépendante de la pression et de la température) et 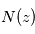 la densité de colonne du composé recherché au-dessus de l'altitude
la densité de colonne du composé recherché au-dessus de l'altitude 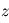 , c'est-à-dire
, c'est-à-dire 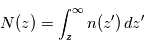 avec
avec 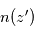 la densité volumique de l'absorbant à l'altitude
la densité volumique de l'absorbant à l'altitude 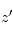 . On peut alors en déduire par différentiation sur les altitudes sondées le profil de densité volumique
. On peut alors en déduire par différentiation sur les altitudes sondées le profil de densité volumique 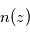 du composé mesuré sur l'intervalle sondé.
du composé mesuré sur l'intervalle sondé.
Cependant, afin de moins dépendre des diverses approximations déjà évoquées, il est préférable d'utiliser un modèle de transfert de rayonnement afin de modéliser les spectres thermiques attendus et de les comparer ensuite aux observations en ajustant les différents paramètres (opération appelée fit en anglais de laboratoire). Notons que la procédure décrite ci-dessus ne fonctionne en pratique que lorsque les raies spectrales sont résolues, c'est-à-dire à une très haute résolution spectrale.
Il n'est en revanche pas possible d'inverser simultanément le profil thermique et le profil d'abondance du composé par la seule observation de ses raies d'absorption. On parle de problème dégénéré.
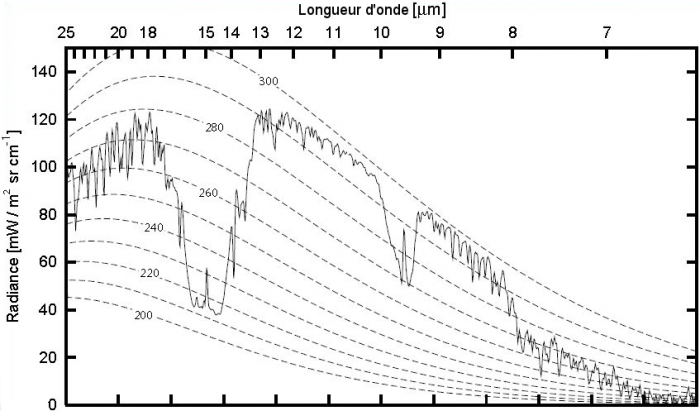
Absorption de quelques gaz dans l'IR thermique
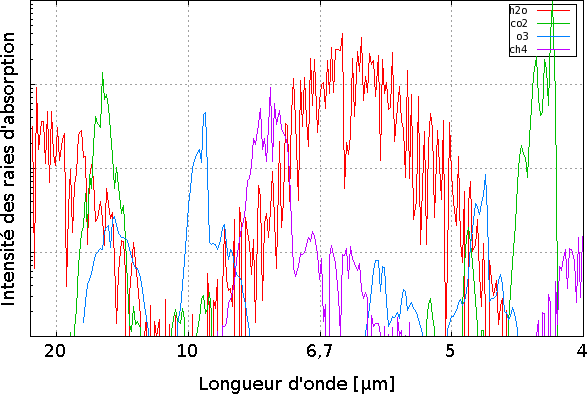
Absorption de la vapeur d'eau (rouge), du dioxyde de carbone (vert), de l'ozone (bleu) et du méthane (violet) dans les conditions standard de température et de pression. L'échelle verticale est logarithmique.
Crédit :
Emmanuel Marcq (à partir de la base de données GEISA 2011) CC-BY-SA
 La méthode des pelures d'oignon
La méthode des pelures d'oignon
L'observation d'une occultation au cours du lever (ou du coucher) de la source à travers l'atmosphère d'une planète permet d'inverser le profil vertical d'extinction 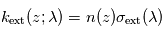 à la longueur d'onde
à la longueur d'onde 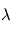 à partir de l'observation des transmissions
à partir de l'observation des transmissions 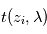 selon différentes altitudes tangentes
selon différentes altitudes tangentes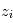 (altitude minimale du rayon lors de sa traversée de l'atmosphère). Un des algorithmes permettant cette inversion est appelé méthode des pelures d'oignon : on découpe l'atmosphère en coquilles sphériques concentriques homogènes à la manière d'un oignon. L'altitude tangente
(altitude minimale du rayon lors de sa traversée de l'atmosphère). Un des algorithmes permettant cette inversion est appelé méthode des pelures d'oignon : on découpe l'atmosphère en coquilles sphériques concentriques homogènes à la manière d'un oignon. L'altitude tangente 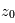 la plus élevée pour laquelle on mesure
la plus élevée pour laquelle on mesure 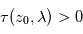 permet de déduire l'extinction locale
permet de déduire l'extinction locale 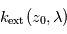 au sein de cette couche la plus extérieure. La profondeur optique observée juste en-dessous, à l'altitude tangente
au sein de cette couche la plus extérieure. La profondeur optique observée juste en-dessous, à l'altitude tangente 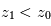 , est alors un peu plus grande. Comme on connaît déjà
, est alors un peu plus grande. Comme on connaît déjà 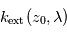 , on en déduit
, on en déduit 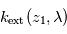 pour la couche immédiatement intérieure. Et ainsi de suite jusqu'au rayon le plus bas pour lequel on puisse mesurer une transmission
pour la couche immédiatement intérieure. Et ainsi de suite jusqu'au rayon le plus bas pour lequel on puisse mesurer une transmission 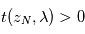 .
.
La mesure des profils d'extinction 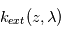 dans l'atmosphère permet alors d'en déduire plusieurs paramètres importants :
dans l'atmosphère permet alors d'en déduire plusieurs paramètres importants :
- si on connaît la section efficace d'exinction
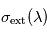 du constituant responsable de l'extinction, on peut en déduire sa densité locale
du constituant responsable de l'extinction, on peut en déduire sa densité locale 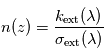 . Si, en plus, le constituant responsable de l'extinction est bien mélangé, alors on sait que son profil vertical
. Si, en plus, le constituant responsable de l'extinction est bien mélangé, alors on sait que son profil vertical 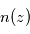 suit la loi hydrostatique, c'est-à-dire une décroissance verticale localement exponentielle selon l'échelle de hauteur atmosphérique locale
suit la loi hydrostatique, c'est-à-dire une décroissance verticale localement exponentielle selon l'échelle de hauteur atmosphérique locale 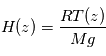 . La décroissance de
. La décroissance de 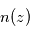 avec l'altitude nous donne alors accès à
avec l'altitude nous donne alors accès à 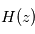 et par conséquent au profil thermique
et par conséquent au profil thermique 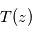 au sein des couches sondées.
au sein des couches sondées. - pour une espèce
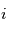 dont le rapport de mélange
dont le rapport de mélange 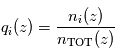 n'est pas verticalement uniforme, la mesure de son profil d'extinction
n'est pas verticalement uniforme, la mesure de son profil d'extinction 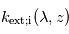 et la connaissance de sa section efficace d'extinction
et la connaissance de sa section efficace d'extinction 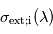 permettent d'en déduire
permettent d'en déduire 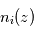 . On peut alors en déduire
. On peut alors en déduire 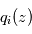 si
si 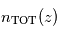 est connu par ailleurs, par exemple grâce à la mesure du profil
est connu par ailleurs, par exemple grâce à la mesure du profil 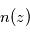 d'un constituant bien mélangé et de rapport de mélange connu.
d'un constituant bien mélangé et de rapport de mélange connu. 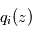 est traditionnellement exprimé en ppmv (parties volumiques par million) pour des constituants mineurs, en pourcentage volumique sinon.
est traditionnellement exprimé en ppmv (parties volumiques par million) pour des constituants mineurs, en pourcentage volumique sinon. - En dehors de l'extinction causée par les gaz, cette méthode donne aussi accès à l'extinction causée par les nuages et brumes (appelés collectivement aérosols) éventuellement présents dans l'atmosphère. Si les mesures des profils d'extinction sont faites à des longueurs d'onde assez éloignées les unes des autres, il est possible de remonter aux propriétés optiques des particules responsables de l'extinction car celles-ci varient habituellement de façon assez faible selon la longueur d'onde (contrairement par exemple aux gaz et leurs nombreuses raies spectrales). Une fois la section efficace d'extinction de ces particules ainsi contrainte, il est possible de déduire à partir des profils d'extinction mesurés le profil de densité volumique des aérosols au sein de l'atmosphère à condition de supposer ou d'avoir par ailleurs accès aux propriétés des diffuseurs individuels (forme, distribution statistique en taille, composition chimique ou au moins indices de réfraction).
Ces occultations sont donc une méthode précieuse de sondage atmosphérique, mais assez délicate à mettre en oeuvre. Il faut en effet pouvoir mesurer de nombreuses transmissions précisément, tout en connaissant parfaitement chacune des altitudes tangentes. Ceci n'est en général possible que pour un satellite en orbite autour de la planète, et nous restreint donc au système solaire.
Méthode dite "par pelure d'oignon"
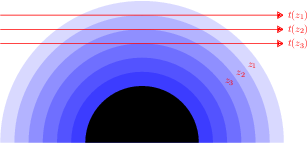
Visualisation géométrique de la méthode d'inversion surnommée "par pelure d'oignon" : la transmission observée
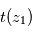
permet, connaissant l'épaisseur traversée, de remonter à
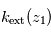
. À partir de là, la transmission
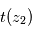
permet, connaissant
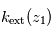
, d'en déduire
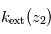
et ainsi de suite.
Crédit :
Emmanuel Marcq CC-BY-SA
Transits primaires
L'observation d'un transit primaire se traduit par une baisse relative de luminosité en provenance de la source partiellement occultée, appelée profondeur du transit, notée 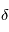 et habituellement mesurée en ppm (parties par million). Pour une planète sans atmosphère, la profondeur est indépendante de la longueur d'onde (la réciproque n'est pas vraie : ainsi un plafond nuageux élevé peut conduire à la même observation, par exemple). En revanche, si l'atmosphère présente une extinction variable selon la longueur d'onde (que ce soit par absorption ou par diffusion Rayleigh par exemple), alors le rayon apparent de la planète (et donc la profondeur du transit) sembleront légèrement plus grands dans les longueurs d'onde où l'atmosphère cause davantage d'extinction.
et habituellement mesurée en ppm (parties par million). Pour une planète sans atmosphère, la profondeur est indépendante de la longueur d'onde (la réciproque n'est pas vraie : ainsi un plafond nuageux élevé peut conduire à la même observation, par exemple). En revanche, si l'atmosphère présente une extinction variable selon la longueur d'onde (que ce soit par absorption ou par diffusion Rayleigh par exemple), alors le rayon apparent de la planète (et donc la profondeur du transit) sembleront légèrement plus grands dans les longueurs d'onde où l'atmosphère cause davantage d'extinction.
On peut ainsi montrer, sous certaines hypothèses simplificatrices, que la variation relative de la profondeur du transit selon la longueur d'onde est liée à celle de la section efficace d'extinction (moyennée verticalement) au sein de l'atmosphère, selon la loi : 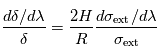 où
où 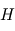 désigne l'échelle de hauteur de l'atmosphère et
désigne l'échelle de hauteur de l'atmosphère et 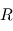 le rayon de la planète. Ces variations sont donc d'autant plus notables que l'échelle de hauteur est grande, ce qui favorise donc les atmosphères très dilatées. C'est par exemple le cas pour les Jupiter chauds (atmosphère légère constituée principalement de H2 et à température élevée).
le rayon de la planète. Ces variations sont donc d'autant plus notables que l'échelle de hauteur est grande, ce qui favorise donc les atmosphères très dilatées. C'est par exemple le cas pour les Jupiter chauds (atmosphère légère constituée principalement de H2 et à température élevée).
Spectroscopie d'un transit primaire

Visualisation de la profondeur d'un transit primaire en fonction de la longueur d'onde. Ici, l'atmosphère est transparente aux grandes longueurs d'onde, et de plus en plus opaque aux courtes longueurs d'onde, ce qui augmente la profondeur du transit.
Crédit :
Emmanuel Marcq CC-BY-SA
L'intérêt d'un transit secondaire réside dans la possibilité d'effectuer une spectroscopie différentielle de la planète : si l'on mesure un spectre 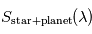 juste avant ou juste après ce transit secondaire, ainsi qu'un spectre
juste avant ou juste après ce transit secondaire, ainsi qu'un spectre 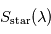 de l'étoile seule pendant ce transit secondaire, on peut en déduire le spectre
de l'étoile seule pendant ce transit secondaire, on peut en déduire le spectre 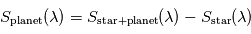 émis ou réfléchi par la planète seule vue à angle de phase nul.
émis ou réfléchi par la planète seule vue à angle de phase nul.
Le spectre 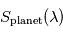 peut alors être analysé comme le serait n'importe quel spectre (par exemple en termes de température ou de composition pour un spectre thermique, ou bien de propriétés des diffuseurs pour un spectre réfléchi). C'est du moins le cas en théorie, car en pratique le faible rapport signal à bruit de tels spectres interdit à ce jour toute analyse trop poussée de ces spectres, de résolution spectrale souvent médiocre.
peut alors être analysé comme le serait n'importe quel spectre (par exemple en termes de température ou de composition pour un spectre thermique, ou bien de propriétés des diffuseurs pour un spectre réfléchi). C'est du moins le cas en théorie, car en pratique le faible rapport signal à bruit de tels spectres interdit à ce jour toute analyse trop poussée de ces spectres, de résolution spectrale souvent médiocre.
Courbe de lumière
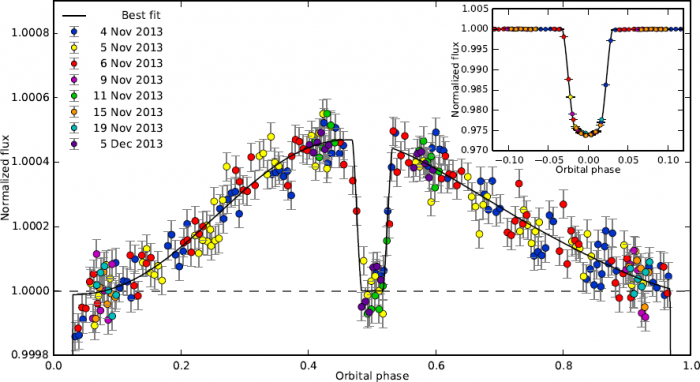
Courbe de lumière lors du transit secondaire de WASP-43b. Le flux en provenance de l'étoile est normalisé à 1. Le surcroît autour du transit secondaire est causé par l'émission thermique de la planète, ce qui a permis de reconstituer son profil thermique. L'insert en haut à droite représente le transit primaire.
Crédit :
Figure tirée de Stevenson et al. (2014)
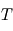 (on peut voir alors leur interaction comme celle d'un gaz de photons perpétuellement absorbés et émis par la matière environnante, et se mettant en équilibre de la sorte). Il existe également des phénomènes d'émission non thermiques (ex: fluorescence, émission laser), mais ils sortent du cadre de ce cours ; certains de ces processus sont vus dans ce chapitre.
(on peut voir alors leur interaction comme celle d'un gaz de photons perpétuellement absorbés et émis par la matière environnante, et se mettant en équilibre de la sorte). Il existe également des phénomènes d'émission non thermiques (ex: fluorescence, émission laser), mais ils sortent du cadre de ce cours ; certains de ces processus sont vus dans ce chapitre.
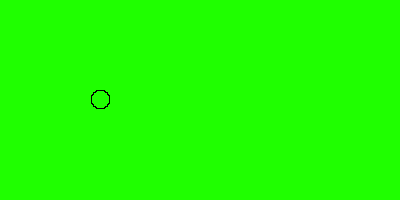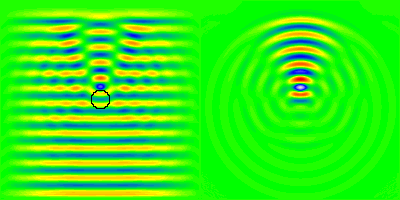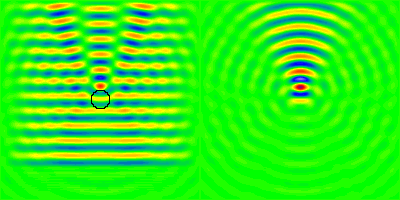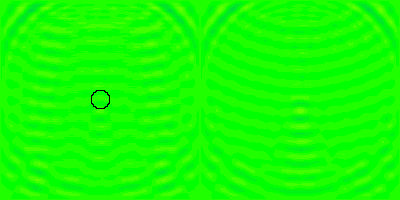
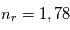 . Le champ électrique total figure à gauche, et la composante diffusée à droite.
. Le champ électrique total figure à gauche, et la composante diffusée à droite.


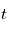 comme le rapport entre l'intensité lumineuse
comme le rapport entre l'intensité lumineuse 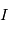 après traversée et celle
après traversée et celle 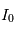 avant la traversée du milieu :
avant la traversée du milieu : 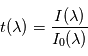 . Cette transmittance vaut 1 si le milieu traversé est transparent, 0 si le milieu est parfaitement opaque, et prend une valeur intermédiaire si le milieu est partiellement opaque. Elle dépend a priori de la longueur d'onde comme la formule l'indique.
. Cette transmittance vaut 1 si le milieu traversé est transparent, 0 si le milieu est parfaitement opaque, et prend une valeur intermédiaire si le milieu est partiellement opaque. Elle dépend a priori de la longueur d'onde comme la formule l'indique.
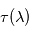 qui se déduit de la transmittance comme suit :
qui se déduit de la transmittance comme suit : ![\tau(\lambda) = - \ln \left[ t(\lambda) \right]](../pages_flux-et-spectre/equations_trans-rad/equation8.png) , soit
, soit 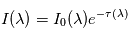 . Il est alors facile de déduire des propriétés mathématiques du logarithme que
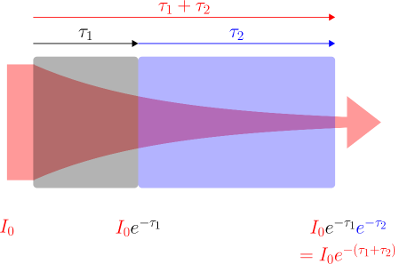
. Il est alors facile de déduire des propriétés mathématiques du logarithme que 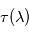 est une grandeur additive le long d'un même rayon (voir figure ci-contre), et qu'elle offre donc un paramétrage naturel de l'abscisse curviligne le long de ce rayon. Il est en outre possible de relier physiquement la variation locale de
est une grandeur additive le long d'un même rayon (voir figure ci-contre), et qu'elle offre donc un paramétrage naturel de l'abscisse curviligne le long de ce rayon. Il est en outre possible de relier physiquement la variation locale de 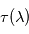 le long d'un rayon à la présence de matière traversée : c'est la loi de Beer-Lambert .
le long d'un rayon à la présence de matière traversée : c'est la loi de Beer-Lambert .
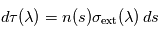 où
où 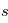 désigne l'abscisse curviligne le long du rayon (croissant dans le sens de propagation),
désigne l'abscisse curviligne le long du rayon (croissant dans le sens de propagation), 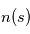 la densité volumique de diffusants et/ou absorbants et
la densité volumique de diffusants et/ou absorbants et 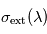 la section efficace d'extinction des diffusants et/ou absorbants. En présence de plusieurs types de diffuseurs et/ou d'absorbeurs, il suffit d'ajouter leurs contributions individuelles. L'évolution de la profondeur optique totale
la section efficace d'extinction des diffusants et/ou absorbants. En présence de plusieurs types de diffuseurs et/ou d'absorbeurs, il suffit d'ajouter leurs contributions individuelles. L'évolution de la profondeur optique totale 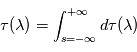 selon la longueur d'onde au cours d'une occultation ou d'un transit offre donc la possibilité à l'observateur de déduire les propriétés matérielles du milieu traversé (densité volumique et nature physique des particules responsables de l'extinction).
selon la longueur d'onde au cours d'une occultation ou d'un transit offre donc la possibilité à l'observateur de déduire les propriétés matérielles du milieu traversé (densité volumique et nature physique des particules responsables de l'extinction).
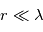 ), ce quelque soit le type d'aérosol (sphérique ou non) : molécules isolées de gaz, micro gouttes, etc.
), ce quelque soit le type d'aérosol (sphérique ou non) : molécules isolées de gaz, micro gouttes, etc.
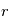 , mais uniquement pour des particules sphériques (gouttes liquides par exemple). Elle tend vers le cas Rayleigh lorsque
, mais uniquement pour des particules sphériques (gouttes liquides par exemple). Elle tend vers le cas Rayleigh lorsque 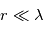 . Pour des particules non sphériques (cristaux, aérosols de Titan, poussières), cette théorie n'est valable qu'en première approximation, et les méthodes utilisées pour aller plus loin sont hors-programme.
. Pour des particules non sphériques (cristaux, aérosols de Titan, poussières), cette théorie n'est valable qu'en première approximation, et les méthodes utilisées pour aller plus loin sont hors-programme.

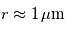 . Aux grandes longueurs d'onde,
. Aux grandes longueurs d'onde, 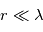 et on se trouve dans le régime Rayleigh (
et on se trouve dans le régime Rayleigh (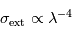 , apparaissant comme une asymptote de pente -4). Pour
, apparaissant comme une asymptote de pente -4). Pour 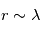 et
et 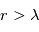 , on se trouve dans le régime de Mie, où la section efficace est presque indépendante de
, on se trouve dans le régime de Mie, où la section efficace est presque indépendante de 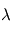 et voisine de la section géométrique des particules.
et voisine de la section géométrique des particules.

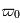 comme la proportion du rayonnement qui est diffusée. Si
comme la proportion du rayonnement qui est diffusée. Si 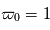 , toute la lumière est diffusée, il n'y a pas d'absorption. En revanche si
, toute la lumière est diffusée, il n'y a pas d'absorption. En revanche si 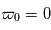 , tout la lumière est absorbée, il n'y a plus de diffusion. En général,
, tout la lumière est absorbée, il n'y a plus de diffusion. En général, 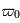 dépend de la longueur d'onde :
dépend de la longueur d'onde : 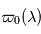 .
.

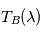 d'un objet est la température du corps noir qui émettrait la même intensité que celle émise par l'objet à la longueur d'onde
d'un objet est la température du corps noir qui émettrait la même intensité que celle émise par l'objet à la longueur d'onde 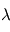 :
: ![I(\lambda) = B\left[\lambda, T_B(\lambda) \right]](../pages_flux-et-spectre/equations_trans-rad/equation33.png) où
où ![B\left[\lambda, T \right]](../pages_flux-et-spectre/equations_trans-rad/equation34.png) désigne la fonction de Planck à la longueur d'onde
désigne la fonction de Planck à la longueur d'onde 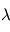 pour un corps noir de température
pour un corps noir de température 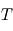 . Comme les courbes représentant les fonctions de Planck ne se croisent jamais, il y a correspondance unique entre
. Comme les courbes représentant les fonctions de Planck ne se croisent jamais, il y a correspondance unique entre 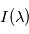 et
et 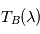 : la température de brillance n'est qu'une autre façon de décrire un spectre. En particulier, elle ne représente pas forcément la température d'un objet physique.
: la température de brillance n'est qu'une autre façon de décrire un spectre. En particulier, elle ne représente pas forcément la température d'un objet physique.
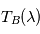 selon la formule
selon la formule 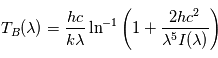 .
.
![T_B(\lambda) \approx T\left[\tau(\lambda) = 1\right]](../pages_flux-et-spectre/equations_trans-rad/equation41.png) avec
avec 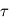 comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :
comptée depuis l'observateur et le long du rayon. Intuitivement, cela résulte d'un compromis dans l'intensité intégrée le long du rayon et reçue par l'observateur :

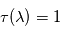 est atteinte plus haut au coeur de la raie (longueur d'onde
est atteinte plus haut au coeur de la raie (longueur d'onde 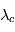 ) que dans les ailes lointaines de la raie (longueur d'onde
) que dans les ailes lointaines de la raie (longueur d'onde 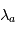 ) :
) : 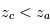 avec
avec 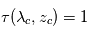 et
et 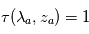 .
.
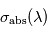 et le profil vertical en densité de l'absorbant
et le profil vertical en densité de l'absorbant 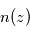 sont connus, il est alors possible de trouver à quelle altitude
sont connus, il est alors possible de trouver à quelle altitude 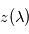 on a
on a ![\tau \left[ z(\lambda) \right] = \int_{z(\lambda)}^{+\infty} \sigma_{\mathrm{abs}}(\lambda) n(z')\,dz' = 1](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation10.png) . On sait alors qu'il règne une température
. On sait alors qu'il règne une température ![T\left[ z(\lambda) \right] \approx T_B(\lambda)](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation11.png) à cette altitude. On a supposé dans ce calcul que la visée de l'observateur pointe verticalement vers le centre de la planète (visée nadir).
à cette altitude. On a supposé dans ce calcul que la visée de l'observateur pointe verticalement vers le centre de la planète (visée nadir).
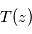 permet, pour chaque longueur d'onde
permet, pour chaque longueur d'onde 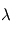 , de retrouver l'altitude
, de retrouver l'altitude 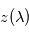 correspondant à la température de brillance observée — en d'autres termes telle que
correspondant à la température de brillance observée — en d'autres termes telle que ![T_B(\lambda) = T\left[z(\lambda)\right]](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation15.png) . Or, on sait que cette altitude correspond à la profondeur optique unité à la longueur d'onde considérée, si bien que l'on a
. Or, on sait que cette altitude correspond à la profondeur optique unité à la longueur d'onde considérée, si bien que l'on a ![\tau \left[ z(\lambda) \right] = \sigma_{\mathrm{abs}}(\lambda) \times N\left[z(\lambda) \right] = 1](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation16.png) où
où 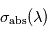 désigne la section efficace d'absorption du composé mesuré (supposée ici indépendante de la pression et de la température) et
désigne la section efficace d'absorption du composé mesuré (supposée ici indépendante de la pression et de la température) et 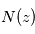 la densité de colonne du composé recherché au-dessus de l'altitude
la densité de colonne du composé recherché au-dessus de l'altitude 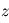 , c'est-à-dire
, c'est-à-dire 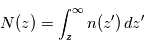 avec
avec 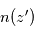 la densité volumique de l'absorbant à l'altitude
la densité volumique de l'absorbant à l'altitude 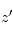 . On peut alors en déduire par différentiation sur les altitudes sondées le profil de densité volumique
. On peut alors en déduire par différentiation sur les altitudes sondées le profil de densité volumique 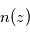 du composé mesuré sur l'intervalle sondé.
du composé mesuré sur l'intervalle sondé.

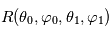 appelée réflectance bidirectionnelle. C'est une fonction à quatre variables, deux pour caractériser la direction du rayon incident (d'angle zénital d'incidence
appelée réflectance bidirectionnelle. C'est une fonction à quatre variables, deux pour caractériser la direction du rayon incident (d'angle zénital d'incidence 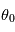 et d'azimuth
et d'azimuth 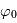 ) et deux pour celle du rayon émergent (d'angle d'émergence zénital
) et deux pour celle du rayon émergent (d'angle d'émergence zénital 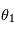 et d'azimuth
et d'azimuth 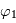 ) . C'est une fonction positive, dont la valeur minimale est nulle dans les directions où l'intensité réfléchie est nulle. Elle ne se déduit pas simplement des fonctions de phase calculables en régime de Rayleigh et de Mie, notamment à cause des phénomènes de diffusion multiple et de la possible contibution de la surface.
) . C'est une fonction positive, dont la valeur minimale est nulle dans les directions où l'intensité réfléchie est nulle. Elle ne se déduit pas simplement des fonctions de phase calculables en régime de Rayleigh et de Mie, notamment à cause des phénomènes de diffusion multiple et de la possible contibution de la surface.
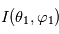 et celle de la source
et celle de la source 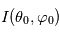 :
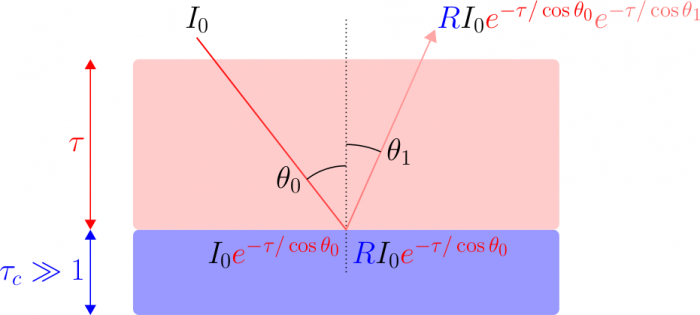
: ![I(\theta_1,\varphi_1) = I(\theta_0,\varphi_0) R(\theta_0,\varphi_0,\theta_1,\varphi_1) \exp \left[ - \tau \left(\frac{1}{\cos \theta_0} + \frac{1}{\cos \theta_1} \right) \right]](../pages_flux-et-spectre/equations_comprendre-meth-nadir/equation31.png) où
où 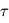 désigne l'épaisseur optique de l'atmosphère au-dessus de la couche réfléchissante (comptée selon la verticale). Le terme en exponentielle provient de la loi de Beer-Lambert pour le rayon incident et le rayon émergent, en tenant compte de leur inclinaison éventuelle qui les amène à traverser des épaisseurs atmosphériques plus importantes que des rayons purement verticaux.
désigne l'épaisseur optique de l'atmosphère au-dessus de la couche réfléchissante (comptée selon la verticale). Le terme en exponentielle provient de la loi de Beer-Lambert pour le rayon incident et le rayon émergent, en tenant compte de leur inclinaison éventuelle qui les amène à traverser des épaisseurs atmosphériques plus importantes que des rayons purement verticaux.
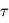 est négligeable, cette méthode permet de mesurer le spectre de l'absorption atmosphérique décrite par
est négligeable, cette méthode permet de mesurer le spectre de l'absorption atmosphérique décrite par 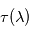 : on a ainsi accès à la densité de colonne intégrée au-dessus de la couche réfléchissante en examinant la profondeur des raies d'absorption des composés atmosphériques. Notons qu'au contraire de l'émission thermique, la présence de composés absorbants se traduit toujours par des raies en absorption et non plus en émission.
: on a ainsi accès à la densité de colonne intégrée au-dessus de la couche réfléchissante en examinant la profondeur des raies d'absorption des composés atmosphériques. Notons qu'au contraire de l'émission thermique, la présence de composés absorbants se traduit toujours par des raies en absorption et non plus en émission.
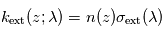 à la longueur d'onde
à la longueur d'onde 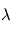 à partir de l'observation des transmissions
à partir de l'observation des transmissions 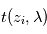 selon différentes altitudes tangentes
selon différentes altitudes tangentes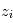 (altitude minimale du rayon lors de sa traversée de l'atmosphère). Un des algorithmes permettant cette inversion est appelé méthode des pelures d'oignon : on découpe l'atmosphère en coquilles sphériques concentriques homogènes à la manière d'un oignon. L'altitude tangente
(altitude minimale du rayon lors de sa traversée de l'atmosphère). Un des algorithmes permettant cette inversion est appelé méthode des pelures d'oignon : on découpe l'atmosphère en coquilles sphériques concentriques homogènes à la manière d'un oignon. L'altitude tangente 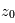 la plus élevée pour laquelle on mesure
la plus élevée pour laquelle on mesure 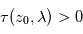 permet de déduire l'extinction locale
permet de déduire l'extinction locale 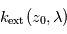 au sein de cette couche la plus extérieure. La profondeur optique observée juste en-dessous, à l'altitude tangente
au sein de cette couche la plus extérieure. La profondeur optique observée juste en-dessous, à l'altitude tangente 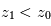 , est alors un peu plus grande. Comme on connaît déjà
, est alors un peu plus grande. Comme on connaît déjà 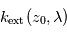 , on en déduit
, on en déduit 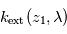 pour la couche immédiatement intérieure. Et ainsi de suite jusqu'au rayon le plus bas pour lequel on puisse mesurer une transmission
pour la couche immédiatement intérieure. Et ainsi de suite jusqu'au rayon le plus bas pour lequel on puisse mesurer une transmission 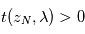 .
.
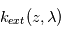 dans l'atmosphère permet alors d'en déduire plusieurs paramètres importants :
dans l'atmosphère permet alors d'en déduire plusieurs paramètres importants :
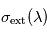 du constituant responsable de l'extinction, on peut en déduire sa densité locale
du constituant responsable de l'extinction, on peut en déduire sa densité locale 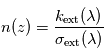 . Si, en plus, le constituant responsable de l'extinction est bien mélangé, alors on sait que son profil vertical
. Si, en plus, le constituant responsable de l'extinction est bien mélangé, alors on sait que son profil vertical 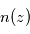 suit la loi hydrostatique, c'est-à-dire une décroissance verticale localement exponentielle selon l'échelle de hauteur atmosphérique locale
suit la loi hydrostatique, c'est-à-dire une décroissance verticale localement exponentielle selon l'échelle de hauteur atmosphérique locale 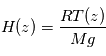 . La décroissance de
. La décroissance de 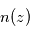 avec l'altitude nous donne alors accès à
avec l'altitude nous donne alors accès à 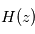 et par conséquent au profil thermique
et par conséquent au profil thermique 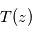 au sein des couches sondées.
au sein des couches sondées.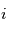 dont le rapport de mélange
dont le rapport de mélange 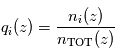 n'est pas verticalement uniforme, la mesure de son profil d'extinction
n'est pas verticalement uniforme, la mesure de son profil d'extinction 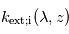 et la connaissance de sa section efficace d'extinction
et la connaissance de sa section efficace d'extinction 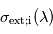 permettent d'en déduire
permettent d'en déduire 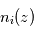 . On peut alors en déduire
. On peut alors en déduire 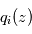 si
si 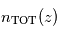 est connu par ailleurs, par exemple grâce à la mesure du profil
est connu par ailleurs, par exemple grâce à la mesure du profil 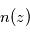 d'un constituant bien mélangé et de rapport de mélange connu.
d'un constituant bien mélangé et de rapport de mélange connu. 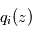 est traditionnellement exprimé en ppmv (parties volumiques par million) pour des constituants mineurs, en pourcentage volumique sinon.
est traditionnellement exprimé en ppmv (parties volumiques par million) pour des constituants mineurs, en pourcentage volumique sinon.
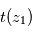 permet, connaissant l'épaisseur traversée, de remonter à
permet, connaissant l'épaisseur traversée, de remonter à 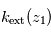 . À partir de là, la transmission
. À partir de là, la transmission 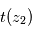 permet, connaissant
permet, connaissant 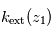 , d'en déduire
, d'en déduire 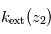 et ainsi de suite.
et ainsi de suite.
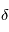 et habituellement mesurée en ppm (parties par million). Pour une planète sans atmosphère, la profondeur est indépendante de la longueur d'onde (la réciproque n'est pas vraie : ainsi un plafond nuageux élevé peut conduire à la même observation, par exemple). En revanche, si l'atmosphère présente une extinction variable selon la longueur d'onde (que ce soit par absorption ou par diffusion Rayleigh par exemple), alors le rayon apparent de la planète (et donc la profondeur du transit) sembleront légèrement plus grands dans les longueurs d'onde où l'atmosphère cause davantage d'extinction.
et habituellement mesurée en ppm (parties par million). Pour une planète sans atmosphère, la profondeur est indépendante de la longueur d'onde (la réciproque n'est pas vraie : ainsi un plafond nuageux élevé peut conduire à la même observation, par exemple). En revanche, si l'atmosphère présente une extinction variable selon la longueur d'onde (que ce soit par absorption ou par diffusion Rayleigh par exemple), alors le rayon apparent de la planète (et donc la profondeur du transit) sembleront légèrement plus grands dans les longueurs d'onde où l'atmosphère cause davantage d'extinction.
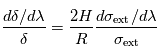 où
où 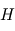 désigne l'
désigne l'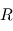 le rayon de la planète. Ces variations sont donc d'autant plus notables que l'échelle de hauteur est grande, ce qui favorise donc les atmosphères très dilatées. C'est par exemple le cas pour les Jupiter chauds (atmosphère légère constituée principalement de H2 et à température élevée).
le rayon de la planète. Ces variations sont donc d'autant plus notables que l'échelle de hauteur est grande, ce qui favorise donc les atmosphères très dilatées. C'est par exemple le cas pour les Jupiter chauds (atmosphère légère constituée principalement de H2 et à température élevée).

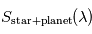 juste avant ou juste après ce transit secondaire, ainsi qu'un spectre
juste avant ou juste après ce transit secondaire, ainsi qu'un spectre 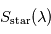 de l'étoile seule pendant ce transit secondaire, on peut en déduire le spectre
de l'étoile seule pendant ce transit secondaire, on peut en déduire le spectre 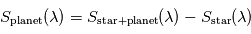 émis ou réfléchi par la planète seule vue à angle de phase nul.
émis ou réfléchi par la planète seule vue à angle de phase nul.
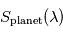 peut alors être analysé comme le serait n'importe quel spectre (par exemple en termes de température ou de composition pour un spectre thermique, ou bien de propriétés des diffuseurs pour un spectre réfléchi). C'est du moins le cas en théorie, car en pratique le faible rapport signal à bruit de tels spectres interdit à ce jour toute analyse trop poussée de ces spectres, de résolution spectrale souvent médiocre.
peut alors être analysé comme le serait n'importe quel spectre (par exemple en termes de température ou de composition pour un spectre thermique, ou bien de propriétés des diffuseurs pour un spectre réfléchi). C'est du moins le cas en théorie, car en pratique le faible rapport signal à bruit de tels spectres interdit à ce jour toute analyse trop poussée de ces spectres, de résolution spectrale souvent médiocre.
