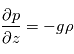Les équilibres géostrophique et cyclostrophique sont deux approximations des équations primitives. Ils sont purement diagnostiques : ils ne contiennent pas de dérivées dans le temps, d'où l'impossibilité de faire des prédictions. Néanmoins, ils sont des outils puissants pour décrire différents écoulements observés dans les planètes.
 L'équilibre géostrophique
L'équilibre géostrophique
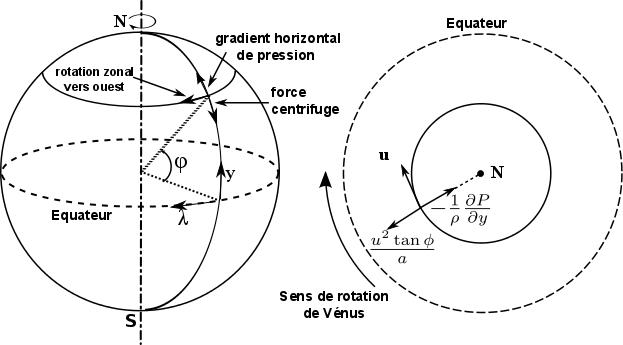
L'approximation géostrophique est un développement des équations primitives utilisée aux moyennes latitudes sur les planètes à rotation rapide (Terre, Mars). On suppose l'équilibre entre la force de Coriolis et la force due au gradient horizontal de pression. La force centrifuge est négligée.
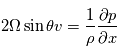
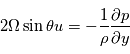
D'après ces équations, lorsque cet équilibre est valide, la vitesse du vent est directement proportionnelle au gradient horizontal de pression. Notez que l'équilibre géostrophique cesse d'être valide autour des latitudes équatoriales.
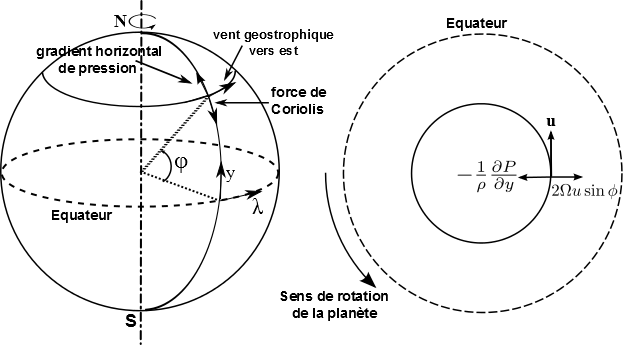
 Vent géostrophique
Vent géostrophique
En combinant les deux composantes de la vitesse, on peut introduir le vent géostrophique comme :
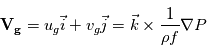
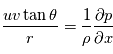
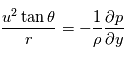
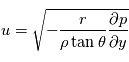
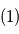 que l'équation du vent cyclostrophique peut être écrite comme :
que l'équation du vent cyclostrophique peut être écrite comme :
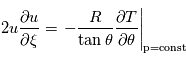
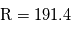 J kg-1 K-1, et
J kg-1 K-1, et 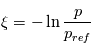 est la coordonnée de pression logarithmique, avec
est la coordonnée de pression logarithmique, avec 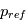 la pression au niveau de référence.
la pression au niveau de référence.
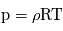
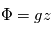 , avec
, avec 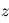 la hauteur et
la hauteur et 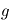 l'accélération gravitationnelle
l'accélération gravitationnelle