Comprendre
Auteur: Sophie Masson
- Notre étoile le Soleil
- L'intérieur solaire
- Le noyau
- La zone radiative
- La zone convective
- L'atmosphère solaire
- La photosphère
- La chromosphère
- La courone
- Le vent solaire
- Le champ magnétique solaire
- La dynamo solaire
- Le champ B à grande échelle
- La formation des régions actives
- L'activité solaire
- Le cycle solaire
- Le cycle solaire
- L'irradiance solaire
- Les éruptions solaires
- La reconnexion magnétique
- Changement de connectivité
- Considération énergétique
- La déroulement d'une éruption
- Observation des éjections des masses coronales
- Chauffage et accélération de particules
- Les signatures radiatives d'une éruption
- Les émissions UV
- Le rayonnement X et
- Le rayonnement radio
- Les relations Soleil-Planète
- Le flux solaire
- L'irradiance solaire
- Impact sur le climat
- Le champ magnétique interplanétaire
- La spirale de Parker
- La connexion Soleil - planète
- Impact des éruptions solaires sur les environnements planétaires
- Propagation des CMEs
- Interaction CMEs planètes
- Propagation des particules énergétiques
Notre étoile le Soleil
L'intérieur solaire
Le noyau
Le noyau
Le noyau est le coeur du Soleil qui s'étend du centre à 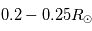 et contient 60% de masse solaire. C'est dans cette région où est produite la majorité de l'énergie solaire rayonnée par la surface. Cette énergie est générée par les réactions de fusion nucléaires de l'hydrogène. En effet, la compression gravitationnelle dans cette région est telle que la densité est de
et contient 60% de masse solaire. C'est dans cette région où est produite la majorité de l'énergie solaire rayonnée par la surface. Cette énergie est générée par les réactions de fusion nucléaires de l'hydrogène. En effet, la compression gravitationnelle dans cette région est telle que la densité est de 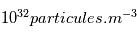 (la densité de l'atmosphère terrestre est de
(la densité de l'atmosphère terrestre est de 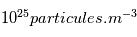 ) et la température atteint
) et la température atteint 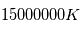 . Pour l'hydrogène, ces conditions impliquent que l'énergie cinétique du à lagitation thermiquedu plasma est supérieure à la repulsion coulombienne présente lorsque 2 particules de même charge se rapprochent.
. Pour l'hydrogène, ces conditions impliquent que l'énergie cinétique du à lagitation thermiquedu plasma est supérieure à la repulsion coulombienne présente lorsque 2 particules de même charge se rapprochent.
La chaine de réaction nucléaire "PP1" au coeur du Soleil conduit à la fusion de 4 hydrogene en un atome d'Hélium et est la plus énergétique :
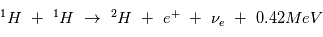
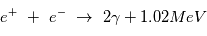
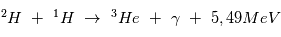
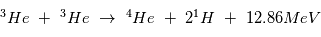
 Température de fusion au coeur du Soleil
Température de fusion au coeur du Soleil
 Energie de la fusion thermonucléaire
Energie de la fusion thermonucléaire
La chaine de réaction nucléaire PP1 décrite dans le cours peut se résumer à la fusion de 4 atomes d'hydrogène pour former un atome d'Helium. Lors de la fusion de 2 atomes, on peut calculer l'énergie libérée grâce à la relation d'Einstein : 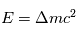 où m est la masse atomique en kg des éléments de la réaction,
où m est la masse atomique en kg des éléments de la réaction, 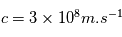 est la vitesse de la lumière et l'énergie E est en Joule.
est la vitesse de la lumière et l'énergie E est en Joule.
Nous rappelons que la masse atomique est la masse moyenne d'un atome. Cette masse se calcul à partir du nombre de particules du noyau et prend éalement en compte la présence d'isotopes (meme nombres de protons et d'électrons mais un nombre différent de neutrons). L'hydrogène 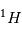 est formé d'un proton et d'un électron. Son isotope le Deuterium
est formé d'un proton et d'un électron. Son isotope le Deuterium 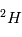 est consititué d'un proton, d'un neutron et d'un électron et le tritium
est consititué d'un proton, d'un neutron et d'un électron et le tritium 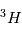 = 1 proton, 2 neutrons et 1 electron. La masse atomique de l'hydrogène est donc 1,0079u.
= 1 proton, 2 neutrons et 1 electron. La masse atomique de l'hydrogène est donc 1,0079u.
Question 1)
Sachant que l'unité de masse atomique 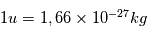 , calculez la masse atomique de 4 atomes d'hydrogène
, calculez la masse atomique de 4 atomes d'hydrogène 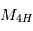 en kg?
en kg?
Question 2)
La masse atomique d'un atome d'hélium est 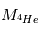 est 4.0026 u. En utilisant la relation masse-énergie d'einstein, calculer l'énergie libérée lors de la fusion de 4 atomes d'hydrogènes en un atome d'hélium.
est 4.0026 u. En utilisant la relation masse-énergie d'einstein, calculer l'énergie libérée lors de la fusion de 4 atomes d'hydrogènes en un atome d'hélium.
Question 3)
Quelle est la fraction de masse d'hydrogène convertie en énergie ?
Question 4)
En considérant que seule 10% de la masse totale du Soleil est de l'hydrogène et peut être convertie en énergie, calculez l'énergie totale générée par fusion thermonucléaire.
Question 5)
L'énergie perdue par le Soleil par irradiation est 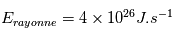 . Estimez alors le temps de vie du Soleil pour consommer tout son hydrogène.
. Estimez alors le temps de vie du Soleil pour consommer tout son hydrogène.
La zone radiative
La zone radiative
La zone radiative se situe entre 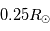 et
et 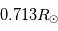 . C'est dans cette zone que l'énergie produite au coeur du soleil est transportée par rayonnement jusqu'à la zone convective. La densité et la température diminuent respectivement d'un facteur 1000 et 10 dans cette région. Les réactions de fusion ne sont alors plus possibles et les photons en provenance du coeur entrent en collision avec les particules du plasma ambient. Lors de ces collisions l'énergie du photon est absorbée par les particules, qui sont alors exitées. Lors de leur desexitation, un photon de plus faible énergie est émis. Lelibre parcours moyen d'un photon dans la zone radiative est très faible, i.e., un photon subit de nombreuses collisions, ce qui a comme effet de ralentir leur sortie de la zone radiative. Au lieu de traverser la zone en 2.5 secondes, ils leur faut plus d'un million d'années pour atteindre la surface solaire.
. C'est dans cette zone que l'énergie produite au coeur du soleil est transportée par rayonnement jusqu'à la zone convective. La densité et la température diminuent respectivement d'un facteur 1000 et 10 dans cette région. Les réactions de fusion ne sont alors plus possibles et les photons en provenance du coeur entrent en collision avec les particules du plasma ambient. Lors de ces collisions l'énergie du photon est absorbée par les particules, qui sont alors exitées. Lors de leur desexitation, un photon de plus faible énergie est émis. Lelibre parcours moyen d'un photon dans la zone radiative est très faible, i.e., un photon subit de nombreuses collisions, ce qui a comme effet de ralentir leur sortie de la zone radiative. Au lieu de traverser la zone en 2.5 secondes, ils leur faut plus d'un million d'années pour atteindre la surface solaire.
Couches internes et externes du Soleil
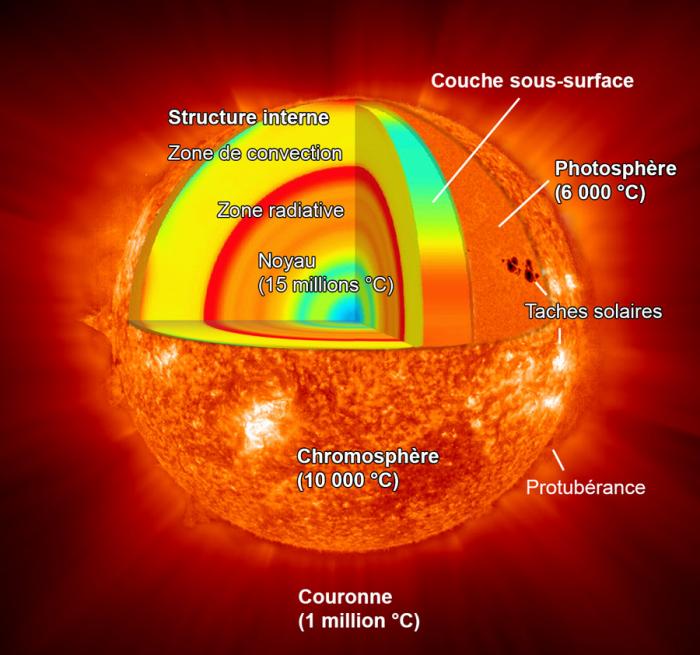
Crédit :
NASA
La zone convective
La zone convective
La dernière couche interne est la zone convective. Cette dernière couche couvre les 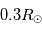 restant. Elle ne contient que 2% de la masse solaire et la température chute de
restant. Elle ne contient que 2% de la masse solaire et la température chute de 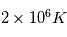 à
à 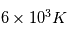 . Comme dans le cas d'une casserole d'eau bouillante, la chaleur est tranportée de la base de la zone convective à la surface solaire par le mécanisme de convection. En effet, lorsque la variation 'ou gradient' de température devient trop élevé, le rayonnement ne peut evacuer toute l'énergie et des régions vont être chauffées plus que d'autres. Ces zones plus chaudes vont alors se déplacer vers la surface sous l'effet de la poussée d'Archimède et engendrer ainsi des mouvements de matière déclenchant la convection.
Les cellules de convection sont d'ailleurs observables à la surface solaire dans la gamme visible des longueurs d'ondes. C'est la granulation, voir le film réalisé à partir des observation du pic du midi avec un filtre a
. Comme dans le cas d'une casserole d'eau bouillante, la chaleur est tranportée de la base de la zone convective à la surface solaire par le mécanisme de convection. En effet, lorsque la variation 'ou gradient' de température devient trop élevé, le rayonnement ne peut evacuer toute l'énergie et des régions vont être chauffées plus que d'autres. Ces zones plus chaudes vont alors se déplacer vers la surface sous l'effet de la poussée d'Archimède et engendrer ainsi des mouvements de matière déclenchant la convection.
Les cellules de convection sont d'ailleurs observables à la surface solaire dans la gamme visible des longueurs d'ondes. C'est la granulation, voir le film réalisé à partir des observation du pic du midi avec un filtre a 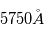 . La taille d'un granule est d'environ 1 Mm.
. La taille d'un granule est d'environ 1 Mm.
La granulation

A changer en Film
Crédit :
Observations Pic du Midi
A la différence de la zone radiative qui est considérée en rotation rigide, i.e., que la vitesse de rotation est identique quelque soit la latitude, la zone convective présente une rotation différentielle. Les pôles tournent plus vite que l'équateur. La région d'interface entre ces deux couches s'appelle la tachocline. Cette région est particulièrement importante puisque l'on pense que le champ magnétique solaire est généré et amplifié dans cette région. Comme nous le verrons par la suite, le champ magnétique est la base de l'activité éruptive solaire.
L'atmosphère solaire
La photosphère
La photosphère
La photosphère est la région où la densité devient suffisament faible pour que le milieu soit 'optiquement mince' (i.e. les photons s'échappent directement sans subir de collisions). Cette couche est de quelques kilomètres seulement et définie la surface solaire observable dans le domaine visible. C'est sur la photosphère que l'on observe les tâches solaires comme on le voit sur l'image ci-contre.
Image de la photosphère

Image de la photosphère en NiI (gauche) et CaII (droite) faite à l'Observatoire de Meudon avec le spectroheliographe.
Crédit :
Obs. de Meudon
Le rayonnement photosphérique peut être traité dans le cadre de l'approximation du corps noir. En effet, de part les nombreuses collisions subies par les photons durant leur trajets vers la surface, le Soleil est à l'équilibre thermodynamique. C'est à dire que le spectre d'émission (i.e., evolution de la puissance émise en fonction de la longueur d'onde) de l'étoile peut etre modélisé pour une temperature donnée.
Cette relation est donnée par la loi de Planck qui relie la puissance rayonée par angle solide et les longueurs d'ondes du rayonnement :
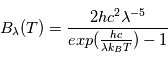
En utilisant cette relation et la mesure du spectre solaire, on peut déterminer la température effective de la photosphère solaire. Pour retrouver la relation entre longueur d'onde et température, il faut déterminer le valeur de la longueur d'onde à laquelle la luminance spectrale B est maximale, i.e., 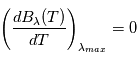 . On obtient alors la loi de Wien telle que:
. On obtient alors la loi de Wien telle que: 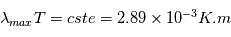
 Détermination de la température de surface du Soleil
Détermination de la température de surface du Soleil
Le maximum d'émission du spectre solaire est aux alentours de 500 nm (couleur verte). Ce maximum d'émission correspond à une température qui définie également la puissance rayonnée (Luminosité) par le Soleil (équivalent à une sphère de rayon R), telle que 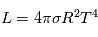 avec la constante de Stefan Boltzman
avec la constante de Stefan Boltzman ![\sigma = 5.67 \times 10^-8 [W.m^{-2}.K^{-4}]](../pages_etoile-planete/equations_atmosphere/equation5.png)
Question 1)
En supposant le Soleil comme un corps noir, calculez la température de surface pour le maximum d'émission à 500 nm.
Question 2)
Connaissant la température d'émission du Soleil et sachant que la puissance rayonnée par le Soleil est 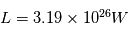 , estimez le rayon solaire.
, estimez le rayon solaire.
La chromosphère
La chromosphère
La chromosphère est une région d'environ 1000 km au dessus de la photopshère où la densité décroit mais la température augmente de 4200K à environ 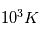 . Alors que la chute en densité avec l'altitude est attendue pour une atmosphère, l'augmentation de la température est toujours un domaine de recherche actif. La chromosphère étant plus ténue que la photosphère, l'approximation du corps noir n'est plus valide, c'est alors les interactions photon-matière qui dominent l'émission.
. Alors que la chute en densité avec l'altitude est attendue pour une atmosphère, l'augmentation de la température est toujours un domaine de recherche actif. La chromosphère étant plus ténue que la photosphère, l'approximation du corps noir n'est plus valide, c'est alors les interactions photon-matière qui dominent l'émission.
En l'absence d'éruption, cette couche atmosphérique est observée principalement à 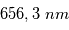 qui correspond à la raie
qui correspond à la raie 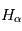 de l'hydrogène. Pour déterminer les longueurs d'ondes des raies atomiques de l'hydrogène, on utilise le modèle atomique de Bohr. Un atome d'hydrogène est composé d'un électron en orbite autour du noyau. Cet électron peut se trouver sur différentes orbites en fonction de l'énergie du système. L'un des postulats de Bohr est la quantification du moment cinétique, et donc que l'énergie totale de l'électron sur une orbite donnée est aussi quantifiée. On peut en effet montrer que l'énergie totale d'un électron est :
de l'hydrogène. Pour déterminer les longueurs d'ondes des raies atomiques de l'hydrogène, on utilise le modèle atomique de Bohr. Un atome d'hydrogène est composé d'un électron en orbite autour du noyau. Cet électron peut se trouver sur différentes orbites en fonction de l'énergie du système. L'un des postulats de Bohr est la quantification du moment cinétique, et donc que l'énergie totale de l'électron sur une orbite donnée est aussi quantifiée. On peut en effet montrer que l'énergie totale d'un électron est :
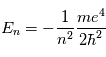
où n = 1, 2, 3,... est le niveau d'énergie et 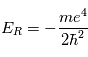 est l'énergie de Rydberg et correspond à l'état d'énergie le plus bas pour n=1. Pour déterminer l'énergie du photon émis/absorbé pour passer d'un niveau
est l'énergie de Rydberg et correspond à l'état d'énergie le plus bas pour n=1. Pour déterminer l'énergie du photon émis/absorbé pour passer d'un niveau 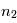 à
à 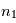 , il suffit de calculer la différence d'énergie entre les 2 niveaux :
, il suffit de calculer la différence d'énergie entre les 2 niveaux : 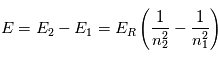
Lorsque l'électron absorbe ou rayonne un photon, il acquiert ou perd respectivement de l'énergie. La quantité d'énergie correspondant à l'aborption ou à l'émission d'un photon est : 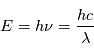
où 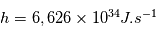 est la constante de Planck,
est la constante de Planck, 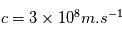 est la vitesse de la lumière,
est la vitesse de la lumière, 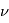 et
et 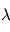 sont respectivement la fréquence et la longueur d'onde du photon émis ou absorbé. En égalisant les 2 expressions définissant l'énergie d'un photon, on obtient une expression pour déterminer la longueur d'onde du photon émis :
sont respectivement la fréquence et la longueur d'onde du photon émis ou absorbé. En égalisant les 2 expressions définissant l'énergie d'un photon, on obtient une expression pour déterminer la longueur d'onde du photon émis : 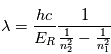
En plus de la chromosphère, d'autres structures contenant du plasma similaire au plasma chromosphérique sont observables à plus haute altitude en 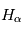 . C'est le cas par exemple des protubérances solaires. Ces structures seront présentées plus en détails dans la partie activité solaire.
. C'est le cas par exemple des protubérances solaires. Ces structures seront présentées plus en détails dans la partie activité solaire.
La chromosphère en H alpha
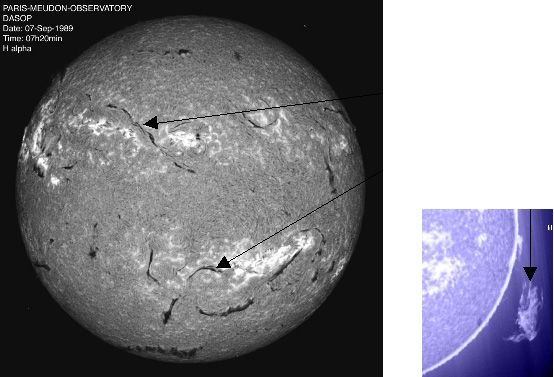
Image du Soleil en entier observé dans la raie
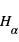
de l'hydrogène. A gauche : Les taches blanches correspondent à des région en émission alors que les structures filamentaires en noire correspondent à l'absorption. Les structures noires sont des filaments, l'équivalent des protubérance que l'on observe au limbe solaire vue sur l'image de droite).
Crédit :
Observatoire de Paris-Meudon
 Emission chromosphérique
Emission chromosphérique
Question 1)
La série de Balmer définie les raies d'émission de l'atome d'hydrogène correspondant aux transitions entre le sniveaux n=2 et n=5. Déterminez le différentes longueurs asssociées aux différentes transitions.
La courone
La couronne solaire
La dernière couche atmosphérique est la couronne solaire. La densité continue à décroitre tandis que la température a continué à augmenter pour atteindre 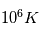 . Elle s'étend de la chromosphère à environ quelques rayons solaires. Au dela de la couronne s'étend le milieu interplanétaire ou héliosphère qui englobe tout notre système solaire jusqu'à l'héliopause, interface avec le milieu interstellaire.
. Elle s'étend de la chromosphère à environ quelques rayons solaires. Au dela de la couronne s'étend le milieu interplanétaire ou héliosphère qui englobe tout notre système solaire jusqu'à l'héliopause, interface avec le milieu interstellaire.
Comme la chromosphère, une des caractéristique principale de la couronne est que la dynamique du milieu est contrainte par le champ magnétique, contrairement à l'interieur solaire et la photosphère où le plasma domine. Cette propriété découle du théorème du gel qui montre que le plasma est couplé au champ magnétique. La nature ionisée du plasma implique que lorsqu'un champ magnétique est présent, le déplacement du plasma conduit au déplacement du champ magnétique et vice versa.
Pour un plasma magnétisé, le régime physique du milieu est défini par le 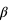 du plasma qui donne le rapport entre la pression cinétique,
du plasma qui donne le rapport entre la pression cinétique, 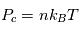 , et la pression magnétique,
, et la pression magnétique, 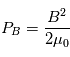 , tel que :
, tel que :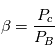 . Lorsque le champ magnétique domine,
. Lorsque le champ magnétique domine, 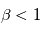 , c'est le cas de la couronne et lorsque le plasma domine
, c'est le cas de la couronne et lorsque le plasma domine 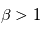 , c'est le cas de la photosphère.
, c'est le cas de la photosphère.
Théorème du gel

Illustration du théorème du gel.
Crédit :
Obs. de Paris
De nombreuses structures magnétiques sont présentes dans la couronne. Ces structures coronales consituent la base de l'activité solaire, éruptive ou non, et sont définies par le champ magnétique. Pour comprendre leur évolution et leur role, il est donc nécessaire de comprendre tout d'abord la formation et le role du champ magnétique solaire.
Lors d'une eclipse naturelle ou articifielle, on peut observé les structures magnétiques de la couronne via l'émission du plasma se déplacant le long du champ magnétique.
La température élevée permet d'avoir un taux élevé d'ionisation (= perte d'un ou plusieurs électrons d'un atome suite à l'interaction avec un photon) des ions lourds tel que le Fer. Comme pour l'hydrogène, l'ionisation d'un élément lourd conduit à l'émission de photons. La couronne solaire émet majoritairement en Ultra-Violet et en rayon X de quelques keV.
Eclipse et structures coronale

Le vent solaire
Le vent solaire
Le vent solaire est un flot de plasma balayant tout le système solaire. Dans le cas d'une atmosphère sans champ magnétique, le fluide est soumis à un gradient en 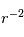 causé par le champ de gravité de l'étoile elle-même. En résolvant les équations de l'hydrodynamique on trouve une infinité de solution. L'unique solution stable est celle où la vitesse du fluide augmente jusqu'a atteindre la vitesse du son (= vitesse caractéristique de la propagation de l'information dans un fluide), c'est la solution trans-sonique. Dans le cas d'une atmosphère magnétisée comme la couronne solaire, ce sont les équations de la magnétohydrodynamique (ou MHD) qu'il faut résoudre. On peut alors montrer numériquement que la solution stable est la solution trans-alfvènique (= vitesse caractéristique de la propagation de l'information dans un plasma magnétisé).
causé par le champ de gravité de l'étoile elle-même. En résolvant les équations de l'hydrodynamique on trouve une infinité de solution. L'unique solution stable est celle où la vitesse du fluide augmente jusqu'a atteindre la vitesse du son (= vitesse caractéristique de la propagation de l'information dans un fluide), c'est la solution trans-sonique. Dans le cas d'une atmosphère magnétisée comme la couronne solaire, ce sont les équations de la magnétohydrodynamique (ou MHD) qu'il faut résoudre. On peut alors montrer numériquement que la solution stable est la solution trans-alfvènique (= vitesse caractéristique de la propagation de l'information dans un plasma magnétisé).
Bien que permettant d'expliquer la formation d'un vent stellaire, l'approche dynamique des atmosphères décrite ci-dessus ne permet pas d'expliquer certaines mesures dans le cas du Soleil. La sonde Ulysses, mission spatiale conjointe de la NASA et de l'ESA, a été lancée en 1990 pour être mise en orbite polaire autour du Soleil. La sonde a permis de mesurer in-situ les vitesses du vent solaire et a montre qu'en période de minimum solaire, la vitesse aux pôles est presque 2 fois plus rapide que la vitesse à l'équateur. L'approche dynamique ne permet pas non plus d'expliquer pourquoi en période de maximum solaire le vent à l'équateur a tendance à être plus rapide et elle n'explique pas non plus les variations de la composition chimique du plasma mesuree dans le vent a 1 UA du Soleil. La formation d'un vent solaire qui serait en accord avec les observations est encore un sujet de recherche très actif. Une des pistes explorée est notamment la dynamique des structures à grande échelle de la couronne soumise à la reconnexion magnétique.
Les sondes spatiales Parker Solar Probe ( NASA, lancement 2018) et Solar Orbiter (ESA, lancement 2020) ont pour but de se rapprocher considerabelement du Soleil pour mesurer les parametres du vent solaire pres de notre etoile. Ces sondes sortiront egalement de l'ecliptique comme Ulysses afin d'obtenir des mesures aux poles.
Données du vent solaire
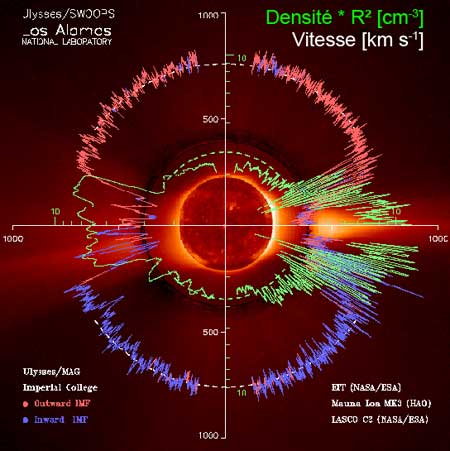
Vitesses du vent solaire mesurées par la sonde Ulysse, en fonction de la latitude dans le milieu interplanétaire, en période de minimum solaire. La séparation entre vent rapide (en bleu –hémisphère Sud - et rouge –hémisphère Nord) et lent a lieu à ± 15°. La densité (en vert) est plus élevée dans les régions de vent lent. Les axes indiquent les valeurs de vitesse en km.s-1. Les petites graduations aux environs de 700 km.s-1 donnent l'échelle des densités (en cm-3)
Crédit :
ULYSSES / ESA
Le champ magnétique solaire
La dynamo solaire
Le champ magnétique est le moteur de l'activité solaire. Ce champ magnétique est généré spontanément, amplifié et auto-entretenu grâce à l'effet dynamo qui consiste à convertir l'énergie mécanique en énergie électromagnétique. Pour le soleil, cet effet dynamo se développe au niveau de la tachocline, où la rotation différentielle entre zone radiative et convective fournit les conditions nécessaires : un fluide conducteur, de l'énergie cinétique par mouvement de rotation, et des mouvements de convection.
L'effet dynamo est quasi-unaniment accepté comme étant le mécanisme de base pour la création et le maintien du champ magnétique solaire. Cependant, les détails de la théorie sont toujours débatus et constitue actuellement un domaine actif de recherche.
En effet, alors que l'effet dynamo est capable de produire un champ magnétique, le Soleil fournit de fortes contraintes observationnelles sur l'évolution spatiale et temporelle du champ magnétique généré. La théorie de l'effet dynamo doit notamment permettre de reproduire :
- Le cycle de 11 ans : Le champ magnétique solaire est à grande échelle dipolaire. Tout les 11 ans, les pôles magnétiques s'inversent.
- le diagramme papillon : Le champ magnétique solaire émerge localement à la surface et forment les taches solaires. Sur plusieurs cycle de 11 ans, l'évolution spatiale des taches solaires au cours du temps de ces régions présente un schéma périodique
Diagramme papillon
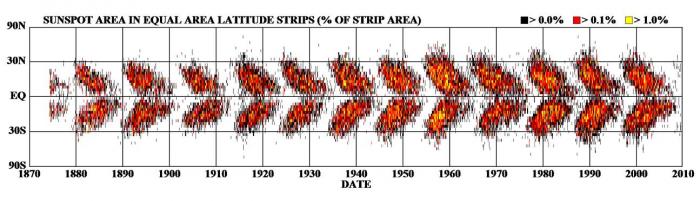
Evolution au cours du temps de la position en latitude des taches solaires à la surface du disque solaire.
Crédit :
irfu. cea.fr
Le champ B à grande échelle
Le champ magnétique global du soleil est dipolaire. Pour représenter les lignes de force de ce champ magnétique il suffit de déterminer la forme du champ magnétique dans l'espace pour un dipole magnétique localisé au centre du Soleil. L'expression d'un tel champ magnétique à une distance suffisament grande du dipole magnetique est donné par:
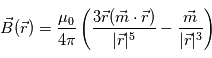 . En coordonnées cylindrique on définit
. En coordonnées cylindrique on définit 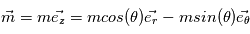 et
et 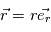 comme illustré sur le shéma ci-contre (haut).
En développant cette expression, on obtient :
comme illustré sur le shéma ci-contre (haut).
En développant cette expression, on obtient : 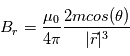 et
et 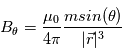 . On ontient une solution paramétrique en fonction de r et
. On ontient une solution paramétrique en fonction de r et 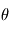 . En calculant les lignes de forces telle que, en tout point, une ligne de force est colinéaire au champ B, i.e.,
. En calculant les lignes de forces telle que, en tout point, une ligne de force est colinéaire au champ B, i.e., 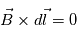 , on obtient un champ B dans l'espace
, on obtient un champ B dans l'espace 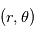 .
.
géométrie du dipole solaire
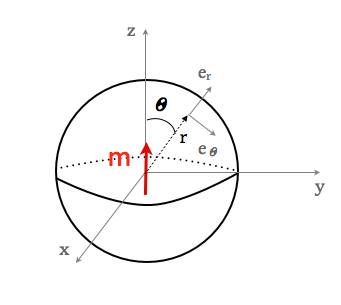
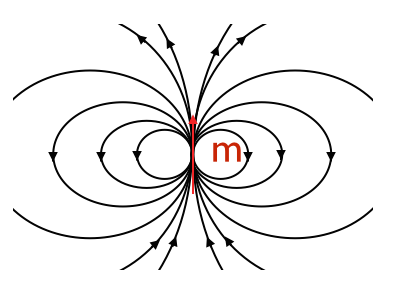
Haut : Géométrie pour calculer le champ magnétique du dipole solaire B, à partir d'un moment magnétique m localisé au centre du Soleil. Bas : Lignes de champs générées par un moment magnétique m.
La structure dipolaire du champ magnétique solaire à grande échelle est modifiée par la présence d'un vent solaire. Le vent est le flot de plasma qui constitue l'héliosphère. En s'éloignant de la surface solaire, l'amplitude du champ magnétique diminue, i.e., la pression magnétique diminue et le 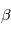 du plasma augmente pour atteindre des valeurs
du plasma augmente pour atteindre des valeurs 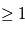 . La pression dynamique du plasma est alors la variable dominante. Le vent solaire étant majoritairement un flot radial de plasma, ceci a pour conséquence d'étendre les lignes de champ magnétique jusqu'au limite de l'héliosphère. Le champ magnétique coronal à grande échelle est alors défini par l'équilibre entre la pression dynamique du plasma et la tension magnétique du champ dipolaire.
. La pression dynamique du plasma est alors la variable dominante. Le vent solaire étant majoritairement un flot radial de plasma, ceci a pour conséquence d'étendre les lignes de champ magnétique jusqu'au limite de l'héliosphère. Le champ magnétique coronal à grande échelle est alors défini par l'équilibre entre la pression dynamique du plasma et la tension magnétique du champ dipolaire.
Dans la couronne solaire, la présence du vent conduit alors à 'ouvrir' les lignes de champ magnétique externe du dipole solaire. On distingue 2 types de structures de base du champ magnétique coronal :
- les trous coronaux polaires : champ magnétique ouvert aux pôles
- les streamers: boucles coronales fermées à grande échelle qui connectent les 2 hemisphères solaires
La nature du champ magnétique coronal est importante puisqu'elle définie si le plasma coronal reste confiné dans les régions fermées où si le plasma s'échappe vers l'espace interplanétaire le long des lignes de champ ouvertes.
Pour déterminer le champ magnétique coronal en équilibre tel que défini plus haut, il faut résoudre les équations de la magnéto-hydrodynamique. Il n'existe pas de manière simple de résoudre analytiquement ces équations et une approche numérique est nécessaire.
Le champ magnétique solaire à grande échelle

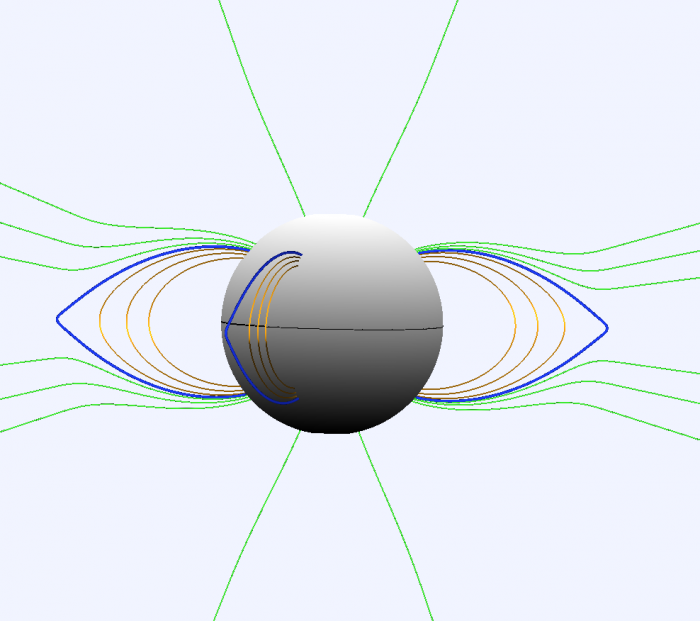
Haut : Lors des éclipses totales, on observe la structure magnétique de la couronne solaire en lumière blanche. Ici l'eclipse du 26 Février 1998 observée au Venezuela. Au pôle on retrouve les structures ouvertes vers l'espace interplanétaire tnadis qu'à l'équateur, les structures sont fermées. Bas : Résultat d' une simulation numérique montrant les lignes de champ magnétique à grande échelle du Soleil. Les lignes vertes sont ouvertes vers l'espace interplanétaire tandis que les lignes bleues et jaunes sont fermées.
Crédit :
Observatoire de Paris
 Détermination de la valeur du champ magnétique
Détermination de la valeur du champ magnétique
Les mesures à la Terre (i.e., à 1 UA) du champ magnétique interplanétaire d'origine solaire donne une valeur de BIMF(1UA)~5.10-5 G.
A partir de cette mesure, nous cherchons à déterminer la valeur du moment magnétique générant le champ magnétique solaire, et nous pourrons ainsi estimer les valeurs type du champ magnétique à la surface solaire.
Question 1)
Exprimer la magnitude du champ magnétique en fonction des composantes déterminées pour un dipole m localisé au centre du Soleil.
Voir les expressions analytiques du cours
Question 2)
Dans le cours l'expression du champ magnétique est exprimé pour des unités SI. En ecrivant l'expression de B en unité CGS, quelle est la valeur valeur du moment magnétique localisé au centre du Soleil
Question 3)
Quelle est la valeur du champ magnétique à la surface solaire au niveau des pôles et au niveau de l'équateur?
La formation des régions actives
L'activité solaire repose sur la formation et la disparition des régions actives. Une région active est une région multi-polaire de forte concentration de champ magnétique, pouvant atteindre 1000 Gauss (10-4 Tesla) en comparaison avec le champ magnétique ambiant de quelques gauss seulement. Leur taille varie de quelques dizaine de 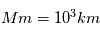 pour les petites régions actives à quelques centaines de Mm pour les plus imposantes. Ces régions actives se forment par le processus d'émergence de flux magnétique de l'interieur solaire vers l'atmosphere. Mais comment passe-t-on d'un champ magnétique dipolaire à un champ mutli-polaire en surface ?
pour les petites régions actives à quelques centaines de Mm pour les plus imposantes. Ces régions actives se forment par le processus d'émergence de flux magnétique de l'interieur solaire vers l'atmosphere. Mais comment passe-t-on d'un champ magnétique dipolaire à un champ mutli-polaire en surface ?
C'est la rotation différentielle de la zone convective (plus rapide aux pôles qu'à l'équateur) qui conduit à l'enroullement des lignes de champ magnétique. De plus, les cellules de convection déforment localement le champ magnétique et il se forment des tubes de flux distincts.
Schéma de l'emergence de flux à grande échelle
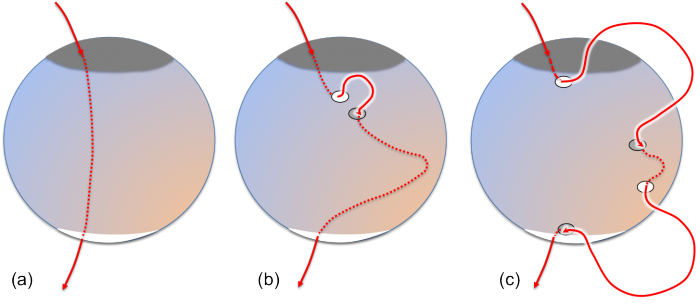
Emergence du champ magnetique suite a la deformation du champ magnetique poloidale sous l'effet de la rotation differentielle. Les lignes pleines sont dans l'atmosphere solaire tandis que les lignes en pointilles sont dans l'interieur solaire.
Crédit :
Obs. de Paris (K.-L. Klein)
Contrairement à ce que l'on pourrait penser, une région active n'emerge pas d'un bloc. Ce sont tout d'abord des fractions de petits tubes de flux qui émergent successivement et fusionnent les un avec les autres pour former les larges concentrations de champ magnetique que l'on observe à la surface solaire. Ces tubes de flux sont transportés vers la surface solaire via les mouvements de convection de la zone convective. Ces tubes de flux émergeants ont une forme en 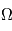 , le vecteur champ magnetique sort de la surface à un pied et 'replonge' dans le soleil à son autre pieds. Cela se traduit par l'apparition d'un bipole magnetique dont les 2 polarités, positive (blanc sur la figure) et négative (en noir sur la figure), correspondent aux deux pieds des boucles magnétiques formées par le tube du flux qui a émergé.
, le vecteur champ magnetique sort de la surface à un pied et 'replonge' dans le soleil à son autre pieds. Cela se traduit par l'apparition d'un bipole magnetique dont les 2 polarités, positive (blanc sur la figure) et négative (en noir sur la figure), correspondent aux deux pieds des boucles magnétiques formées par le tube du flux qui a émergé.
Emergence du champ magnétique

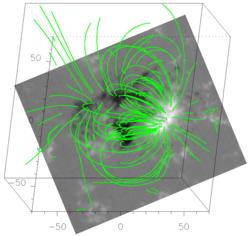
Haut : Mesure du champ magnétique à la surface solaire. On remarque la présence de région active ainsi que de multiples concentrations plus faible de flux magnétique. Bas : L'image de fond représente les mesures du champ magnétique par le satellite SoHO. Les polarités positives sont en blanc et les polarités négatives en noire. Les lignes vertes montrent des lignes de forces du champ magnétique reconstruit tri-dimensionnellement.
Crédit :
LESIA - Observatoire de Paris
Les mesures du champ magnétiques sont obtenues depuis l'espace. Le Solar Dynamics Observatory (NASA), fournit des mesures du champ magnétique à très haute résolution spatiale et temporelle avec son instrument Helioseismic and Magnetic Imager. A partir de ces mesures, il est possible de reconstruire numériquement le champ magnétique dans un volume de la couronne, ce qui permet de connaitre la structure magnétique des régions actives et de la couronne en générale. Le champ magnétique étant l'origine de l'activité solaire, en connaitre les propriétés est un apport essentiel pour l'étude des éruptions.
L'activité solaire
Le cycle solaire
Le cycle solaire
L'activité solaire peut être divisée en 2 catégories : les variations à long terme résultant du cycle solaire et les changements intervenant sur quelques jours voir quelques heures.
Un des indicateurs de l'activite solaire sont les taches solaires. Leur observation à la lunette en lumiere visible débutèrent en 1610 avec Gallilée en Italie, Harriot en Angleterre, Johannes Fabricius en Hollande et le jésuite Christoph Scheiner en Allemagne. Les taches solaires sont des taches sombres qui apparaissent a la surface solaire. Elles correspondent a la presence d'une forte concentration de champ magnetique. Dans ces regions, le champ magnetique est particulierement intense et ne permet pas au gaz de la zone convective d'atteindre la surface via les mouvements de convection. Le gaz chaud n'est donc pas present au sein d'une tache, et celle-ci est ainsi plus froide et apparait donc plus sombre que son environnement.
Le cycle solaire de 11 a été etablit suite aux observations d'un astronome amateur, Samuel Heinrich Schwabe, qui observait le Soleil et ses taches tout les jours pendant pres de 20 ans espérant découvrir une planète a l'intérieur de l'orbite de Mercure. Rudolf Wolf, directeur de l'observatoire de Bern mit en place des observations systématiques des taches à partir de 1843.
Ces taches solaires apparaissent à la surface du Soleil et leur nombres évolue suivant un cycle de 11 ans. C'est l'evolution temporelle du nombre de tache a la surface qui definit le cycle solaire. En période dit de minimum solaire, le nombre de tache est très faible, voire nul. Leur nombre augmente progressivement les premières années du cycle pour atteindre un maximum solaire environ 5 à 7 années apres le minimum. Le nombre de tâches diminue à nouveau jusqu'au minimum suivant.
Edward Walter Maunder (1904) compléta la description en montrant que les taches apparaissaient tout d’abord aux hautes latitudes (maximum 40°) puis de plus en plus bas à mesure que le cycle avançait (minimum 5°). Cette description est connue sous le nom de « Diagramme Papillon ». A cette époque, le caractère magnétique des taches solaires n’était pas connu. C’est Georg Ellery Hale qui le mit en évidence au début du XXe siècle.
Ce cycle de 11 ans appelle le cycle solaire. La période de 11 ans est en fait une valeur moyenne. Entre 1700 et aujourd’hui les cycles ont varié entre 9 ans et 14 ans pour les valeurs extrêmes.
On peut facilement constater d’après la première figure que le nombre de taches au cours de chaque cycle varie énormément. Il est très difficile, encore à l’heure actuelle, de prévoir les niveaux du cycle à venir et de nombreuses équipes y travaillent à travers le monde.
Enfin, le « vrai » cycle solaire est plutôt de 22 ans si l’on tient compte de la polarité globale du Soleil. En regardant le Soleil dans sa globalité (grande échelle), il se comporte comme si une barre aimantée, placée en son centre, tournait de façon plus ou moins régulière. Après 11 ans, les pôles nord et sud sont inversés ; il faut attendre de nouveau 11 ans (en moyenne toujours) pour retrouver l’orientation initiale des pôles. La Terre aussi a vu l'inversion de l'orientation de ses pôles magnétiques dans son histoire. La dernière fois, c’était il y a 740 000 ans …
L’aspect du champ magnétique à grande échelle change considérablement au cours du cycle.
Cycle solaire
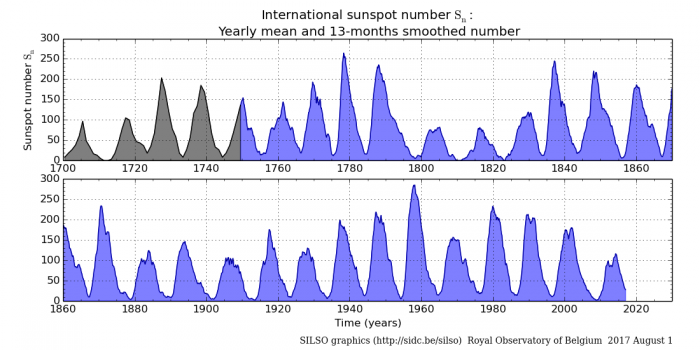

En haut : evolution a long terme du nombre de taches solaires au cours du temps sur 320 ans. En bas : evolution de l'emission en UV de la couronne solaire montrant le cycle d'activite sur 20 ans contenant 2 minima et 1 maximum d'activite solaire.
Crédit :
Royal Obs. of Belgium
L'irradiance solaire
Les éruptions solaires
La reconnexion magnétique
Avant de pouvoir parler d'eruption solaire il nous faut introduire une notion essentielle, la reconnexion magnetique. La reconnexion magnétique est le changement de connectivité des lignes de champs magnétique et est directement due à la dissipation de l'énergie magnétique. C'est le mécanisme de base de l'activité solaire, de l'émergence des régions actives à l'éruption. Nous avons vu au debut du cours que le champ magnetique est gele dans le plasma. Ce theoreme est valable a grande echelle. En effet, si l'on regarde a plus petite echelle, typiquement en dessous du rayon de gyration des electrons, le plasma et le champ magnetique sont decouple. C'est a dire que le champ magnetique peut se deplacer independamment du plasma. Le mecanisme de reconnexion magnetique apparait donc localement lorsqu'une region de diffusion se developpe a petite echelle.
Changement de connectivité
Une des propriétés de la reconnexion est le changement de connectivité. Sur la figure ci-contre, premier panneau, le champ magnétique est initialement anti-parallèle. Puis sur le deuxieme panneau les lignes de champ se rapprochent l'une de l'autre. Une région de diffusion se forme à la frontière. Les lignes de champs echangent leur connectivité dans cette région de diffusion. On peut visualiser cette reconnection comme des lignes de champ qui se brisent et se recollent à l'opposé. Cette description simpliste permet de comprendre le changement de connectivité.
Physiquement, le changement de connectivité résultant de la reconnexion magnétique n'est possible que pour un plasma magnétisé et à de petites échelles spatiales, inférieures aux rayon de gyration des particules chargées. Dans cette situation, le plasma et le champ magnétique sont découplés (trop loin et le théorème du gel n'est plus valide), c'est ce qui permet aux lignes de champ de perdre leur identité et de pouvoir localement changer de direction.
L'équation d'induction est l'équation qui définit l'évolution du champ magnétique. En exprimant l'équations de Faraday,
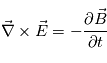 , en utilisant l'équation de Maxwell
, en utilisant l'équation de Maxwell 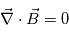 et la loi d'Ohm non généralisé :
et la loi d'Ohm non généralisé : 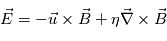 , on obtient l'expression de l'équation d'induction :
, on obtient l'expression de l'équation d'induction : 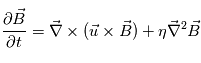 . Avec
. Avec 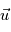 la vitesse du plasma et
la vitesse du plasma et 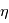 la resistivité électrique du milieu. Le premier terme est le terme d'advection et le second terme est le terme dissipatif.
la resistivité électrique du milieu. Le premier terme est le terme d'advection et le second terme est le terme dissipatif.
Le régime physique d'un plasma magnétisé est défini par son nombre de Reynolds magnétique qui est le rapport entre le terme dissipatif et le terme d'advection, 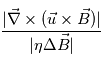 . La couronne solaire étant un très bon conducteur, la resistivité électrique
. La couronne solaire étant un très bon conducteur, la resistivité électrique 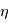 est petite et le reynolds magnétique est alors >> 1 : le terme d'avection domine. La reconnexion magnétique se développe lorsque le terme dissipatif est du même ordre de grandeur que le terme d'advection du champ magnétique. En explicitant le nombre de Reynolds on obtient :
est petite et le reynolds magnétique est alors >> 1 : le terme d'avection domine. La reconnexion magnétique se développe lorsque le terme dissipatif est du même ordre de grandeur que le terme d'advection du champ magnétique. En explicitant le nombre de Reynolds on obtient : 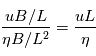 . u est la vitesse caracteristique du plasma , L la longueur caracteristique de la region de dissipation et
. u est la vitesse caracteristique du plasma , L la longueur caracteristique de la region de dissipation et 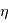 la resistivité électrique du milieu. Si L devient très petit, le terme d'advection diminue et devient comparable au terme dissipatif. Dans la couronne solaire, le mécanisme de reconnexion magnétique se developpera aux petites échelles (L petit).
la resistivité électrique du milieu. Si L devient très petit, le terme d'advection diminue et devient comparable au terme dissipatif. Dans la couronne solaire, le mécanisme de reconnexion magnétique se developpera aux petites échelles (L petit).
Pour que le changement de connectivité opère dans les régions de diffusion, il faut la présence d'un champ électrique parallèle au champ magnétique. C'est cette composante parallèle qui permet de briser le gel magnétique et de conduire au mouvement propre des lignes de champ magnétique. D'apres la loi d'Ohm non-généralisée, le terme 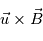 exprime le champ életrique crée par les déplacements du plasma magnétisé à une vitesse u. On peut montrer que le champ électrique parallele ne provient que du rotationnel du champ magnétique. La création d'un champ électrique s'accompagne de la formation d'une nappe de courant (loi de Maxwell-Ampère :
exprime le champ életrique crée par les déplacements du plasma magnétisé à une vitesse u. On peut montrer que le champ électrique parallele ne provient que du rotationnel du champ magnétique. La création d'un champ électrique s'accompagne de la formation d'une nappe de courant (loi de Maxwell-Ampère : 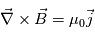 ).
).
Les configurations magnétiques des régions actives sont généralement multi-polaires, ce qui permet d'avoir des zones particulières ou le champ magnétique s'inverse rapidement. Ces zones sont généralement associées à une discontinuité du champ magnétique qui constitue des sites préférentiels pour le développement de la reconnexion magnétique.
Reconnexion magnétique
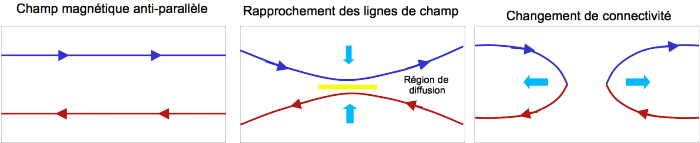
Les lignes de couleurs representent les lignes de champ magnetique. De la gauche vers la droite ce schema montre le changement de connection des lignes de champ qui se cassent et se reforment en se couplant l'une a lautre.
Crédit :
Obs. de Paris
 Exercice
Exercice
Question 1)
Bien que la reconnexion magnétique fasse appelle à des notions compliqués, on peut tout de même se faire une idée du principe en posant le problème le plus simplement possible. Soit un champ magnétique 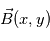 distribué comme le montre le schéma (a ajouter)en coordonnées cartesienne. On suppose alors aucun mouvement de plasma, i.e.,
distribué comme le montre le schéma (a ajouter)en coordonnées cartesienne. On suppose alors aucun mouvement de plasma, i.e., 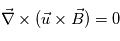 . L'équation d'induction est alors réduite à
. L'équation d'induction est alors réduite à 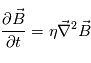 .
Expliciter cette equation pour le champ magnetique donne ci-dessus :
.
Expliciter cette equation pour le champ magnetique donne ci-dessus :
Question 2)
A partir du schema ci-contre, trace l'evolution de bx et by en fonction de y. En utilisant ces profiles , evaluez le signe de leur dérivée seconde :
Question 3)
En deduire l'evolution au cours du temps des composante de bx et by. En conclure comment cela modifie les lignes de champ sur le schema.
Considération énergétique
Le second aspect de la reconnexion réside dans l'éjection brutale de matière s'expliquant par le modèle de Sweet Parker. Ce modèle permet de déterminer la vitesse que doit avoir le fluide plasma à l'entrée et à la sortie de la nappe de courant en fonction de la resistivité du mileu.
Par simplification, considérons une géométrie en 2 dimensions (cf Figure). Pour une nappe de courant de longeur L et d'épaisseur δ, situé sur l'axe d'inversion du champ magnétique, on applique la loi de conservation de la masse. Pour un fluide de densité ρin incident sur la section L de la nappe de courantà uen vitesse uin, on doit avoir : 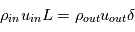 .
.
Avec 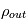 et
et 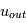 , la densité et la vitesse de sortie du fluide par le coté δ de la nappe de courant.
, la densité et la vitesse de sortie du fluide par le coté δ de la nappe de courant.
En supposant le fluide incompressible, on a d'après l'équation de continuité 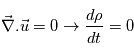 , soit ρin=ρout.
On a alors
, soit ρin=ρout.
On a alors 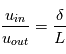
Vitesse d'entrée du fluide : Le modèle de Sweet Parker fait l'hypothèse d'un problème stationnaire, i.e. 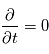 . L'équation d'induction devient alors
. L'équation d'induction devient alors 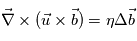 .
Le rapport du terme d'advection et du terme diffusif défini le nombre de Reynolds magnétique. Ce nombre défini le régime physique dans lequel se trouve le système. Pour que la reconnexion ait lieu il faut que le terme diffusif soit du même ordre de grandeur que le terme d'advection, i.e., Rm ~1. En estimant ce nombre de Reynolds à partir des grandeur caractéristique du système, i.e. les différentielles spatiales sont proportionnelles à l'inverse de la longueur caractéristique du système, on obtient :
.
Le rapport du terme d'advection et du terme diffusif défini le nombre de Reynolds magnétique. Ce nombre défini le régime physique dans lequel se trouve le système. Pour que la reconnexion ait lieu il faut que le terme diffusif soit du même ordre de grandeur que le terme d'advection, i.e., Rm ~1. En estimant ce nombre de Reynolds à partir des grandeur caractéristique du système, i.e. les différentielles spatiales sont proportionnelles à l'inverse de la longueur caractéristique du système, on obtient :
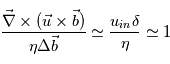
La vitesse d'entrée du plasma est alors : uin~ η/δ pour respecter les lois de conservations. La vitesse d'entrée du fluide ne dépend alors que de la resistivité et de l'épaisseur de la nappe de courant. Notons que plus le rapport entre la longueur et l'épaisseur de la nappe de courant est proche de 1, plus la reconnexion sera rapide pour une vitesse de sortie fixée : la vitesse d'entrée sera de l'ordre de la vitesse de sortie
Vitesse de sortie du fluide : Lors de la reconnexion, on suppose que toute l'énergie magnétique (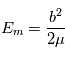 ) est transformée en énergie cinétique, on a :
) est transformée en énergie cinétique, on a : 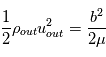 .
Donc
.
Donc 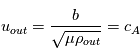 . La vitesse du fluide en sortie de la nappe de courant n'est autre que la vitesse d'Alfvèn. L'éjection de matière accompagnant la reconnexion magnétique est un mouvement Alfvénique. Au site de reconnexion dans la couronne, le champ magmétique est de l'ordre de 500 à 1000 G et la densité est de l'ordre de 108-9 g.cm-3 . La perméabilité magnétique dans la couronne approche celle du vide (
. La vitesse du fluide en sortie de la nappe de courant n'est autre que la vitesse d'Alfvèn. L'éjection de matière accompagnant la reconnexion magnétique est un mouvement Alfvénique. Au site de reconnexion dans la couronne, le champ magmétique est de l'ordre de 500 à 1000 G et la densité est de l'ordre de 108-9 g.cm-3 . La perméabilité magnétique dans la couronne approche celle du vide (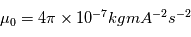 ). On a donc une vitesse d'Alfvèn comprise entre 1000 et 5000 km.s-1. En comparaison avec les vitesses typique de la photosphère de l'ordre de quelques dizaines de km.s-1, le jet de matière en sortie de la nappe de courant est très rapide.
). On a donc une vitesse d'Alfvèn comprise entre 1000 et 5000 km.s-1. En comparaison avec les vitesses typique de la photosphère de l'ordre de quelques dizaines de km.s-1, le jet de matière en sortie de la nappe de courant est très rapide.
A partir des vitesses d'entrée et de sortie du fluide, on estime le nombre de Mack qui représente le taux de reconnection du système tel que : 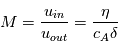 . Pour une vitesse d'Alfvèn et une resistivité η fixées, le taux de reconnection augmente lorsque l'épaisseur de la nappe de courant, δ, est petite. On retrouve le critère nécessaire des petites échellles pour le développement de la reconnection magnétique.
. Pour une vitesse d'Alfvèn et une resistivité η fixées, le taux de reconnection augmente lorsque l'épaisseur de la nappe de courant, δ, est petite. On retrouve le critère nécessaire des petites échellles pour le développement de la reconnection magnétique.
Modèle de Sweet-Parker
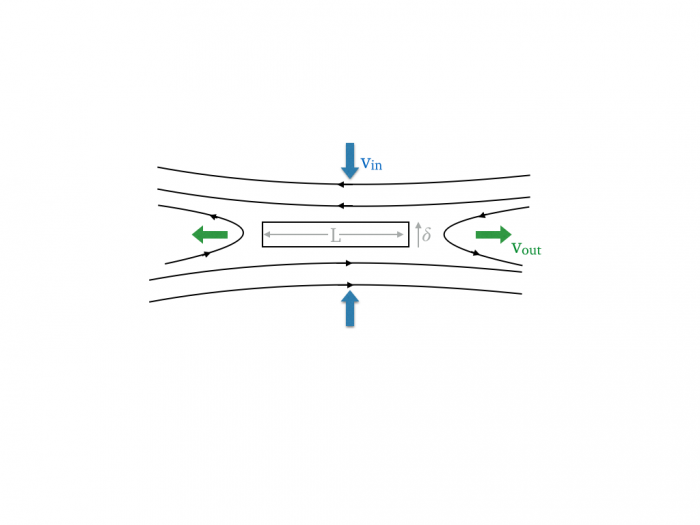
Représentation schématique du modèle de Sweet-Parker. Le rectangle au centre montre la nappe de courant formée à l'interface de champ magnétique opposés.
Crédit :
Obs. de Paris
La déroulement d'une éruption
Le déroulement d'une éruption
Une éruption solaire est causee par la libération d'énergie préalablement emmagasinée sous forme d'énergie magnétique dans les régions actives. Les éruptions solaires sont sans aucun doute le phénomènes les plus énergétiques de notre système solaire, de l'ordre de 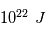 , et ont un impact non négligeables sur les environnement planétaires.
, et ont un impact non négligeables sur les environnement planétaires.
Bien que d'énormes progrès aient été faits grâce aux moyens numériques, il reste encore des questions fondamentales pour comprendre toute la physique mis en jeu lors d'une éruption solaire. Cependant, il est possible de comprendre l'évolution d'un éruption de manière simplifiée et globale.
La première étape est de construire la structure meme de l'éruption, le filament ou protubérance ou tube de flux torsadé (cf Figure). Cela prend en général plusieurs jours. Au niveau de la ligne d'inversion des 2 polarité de la région active, les mouvements photosphériques combinés avec de nouveaux épisodes d'émergence de flux conduisent à la formation d'arcades cisaillées. Ces boucles cisaillées vont alors reconnectées les unes avec les autres pour former un filament (cf animation).
Au niveau de la photosphère, 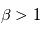 , i.e., les mouvements photospheriques du plasma déplacent les tubes de flux magnétiques émergés dans la couronne. En réponse à ces mouvements photosphériques, le filament s'élève tout d'abord lentement, puis est soudainement éjecté dans l'atmosphère solaire à des vitesses pouvant atteindre plusieurs milliers de km. s-1. C'est une éjection de masse coronale qui va par la suite se propager dans le milieu interplanétaire et le modifier.
, i.e., les mouvements photospheriques du plasma déplacent les tubes de flux magnétiques émergés dans la couronne. En réponse à ces mouvements photosphériques, le filament s'élève tout d'abord lentement, puis est soudainement éjecté dans l'atmosphère solaire à des vitesses pouvant atteindre plusieurs milliers de km. s-1. C'est une éjection de masse coronale qui va par la suite se propager dans le milieu interplanétaire et le modifier.
Le principe de base pour expliquer le decollage impulsif d'une CME est la perte d'équilibre entre les forces appliquées sur le filament. Puisque le champ magnétique domine, on peut considérer que seule la force de Lorentz est active sur le tube de flux. C'est la force entre un courant et le champ magnétique, telle que : 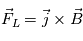 . Cette force peut s'exprimer en fonction de 2 composantes. Sachant que
. Cette force peut s'exprimer en fonction de 2 composantes. Sachant que 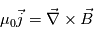 (Equation d'Ampère),
(Equation d'Ampère), 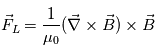 . En utilisant les identité vectorielles, on peut décomposer la force de Lorentz telle que :
. En utilisant les identité vectorielles, on peut décomposer la force de Lorentz telle que : 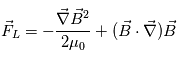 . Le premier terme correspond à la pression magnétique et le deuxieme à la tension magnétique.
. Le premier terme correspond à la pression magnétique et le deuxieme à la tension magnétique.
Schéma pré-éruption
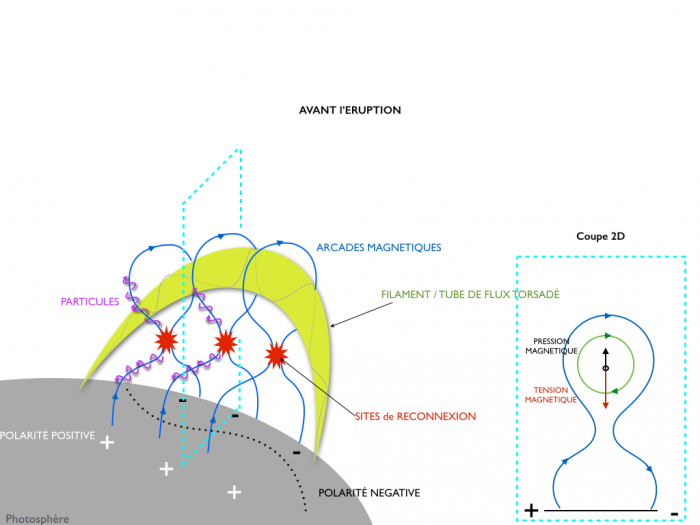
Schéma post-éruption
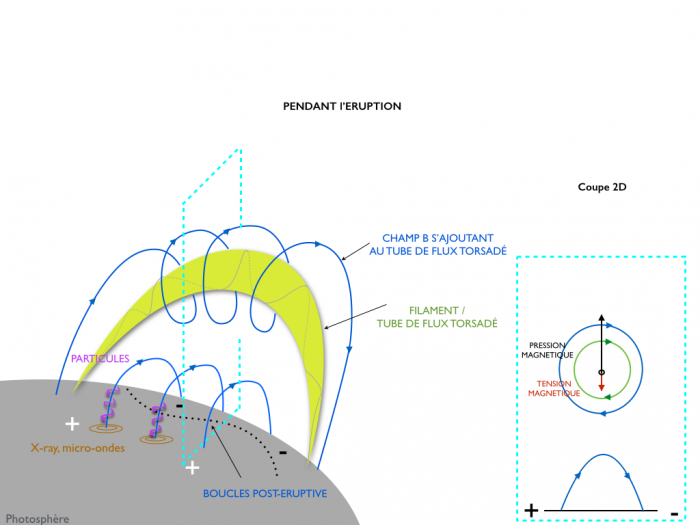
Au debut, le filament est maintenu dans la couronne grace à la tension magnétique des arcades magnétiques du champ ambiant qui est plus grande que la pression magnétique du tube de flux. Au fur et à mesure que le tube de flux s'élève dans la couronne, la tendance s'inverse, ce qui a pour conséquence l'envol du tube de flux qui n'est plus efficacement confiné par le champ B ambiant.
Une conséquence de la montée et de l'éjection du tube de flux est le développement d'une zone de reconnexion magnétique sous le tube de flux (cf Figure). Le changement de connectivité (lignes des champ se 'brisent' et se 'reforment' différemment) dans cette région conduit à la formation de 1) flux magnétique qui s'enroule autour du tube de flux torsadé déjà existant (i.e., augmentant la pression magnétique du tube de flux) et 2) des boucles post éruptive bas dans la couronne.
C'est également dans cette zone spécifique que l'énergie magnétique accumulée dans la région active est transférée sous forme d'énergie thermique et cinétique au plasma ambiant. Lors de l'éjection du tube de flux, une partie de l'énergie est également transférée à la CME sous forme d'énergie cinétique, ayant pour conséquence l'accélération globale de la structure jusqu'à quelques milliers de km.s-1
Observation des éjections des masses coronales
Les filaments, structure à l'origine de l'éjection de masse coronale, s'observent en absorption sur le disque solaire dans les raies Lyman alpha de l'hydrogène. Sur la figure, ce sont les rubans noirs à la surface du disque. Un filament est une structure magnétique qui de part sa géométrie se compose de région convexe, formant des hamacs magnétiques, au sein desquels le plasma coronal peut s'accumuler. Cette matière coronale, plus froide (environ 10 000 K) que son environnement absorbe le rayonnement de la surface solaire d'où sa couleur noire.
Lorsque ces filaments sont observés au limbe solaire (cf figure), ce sont des protubérances solaires. La matière coronale bien que plus froide émet dans certaines longueurs d'onde de l'Ultra-Violet.
Les récentes observations de Solar Dynamics Observatory permet de voir ces filaments à très haute résolution spatiale et temporelle. Sur l'animation ci-contre, on voit clairement que le filament évoule dans un premier temps très lentement puis soudainement accélère et est éjectée.
Une fois éjectée, on observe ce filament éjecté comme une éjection de masse coronale en lumière blanche à l'aide de coronographe (eclipse artificielle). Il est ensuite possible de suivre ces perturbations héliosphériques avec des imageurs dédiés embarqués sur sondes spatiales jusqu'à environ 330 rayons solaires (au dela de l'orbite terrestre). Grace aux mesures in-situ à la Terre du champ magnétique, on peut également obtenir des diagnostics sur l'arrivée de ces structures à la Terre.
Chauffage et accélération de particules
Chauffage et accélération de particules
Une partie de l'énergie dissipée lors de la reconnexion magnétique est convertie en énergie thermique. Le flux de chaleur ainsi généré au site de reconnexion se propage principalement le long des tubes de flux magnétique. Notamment, lors d'une éruption, le flux de chaleur précipite vers la surface solaire le long des boucles post-éruptives et impacte la couche chromopshérique, plus dense que la couronne. Cela entraîne alors un chauffage local du plasma chromosphérique.
Une seconde conséquence de la libération d'énergie est l'accélération de particules. Au site de reconnexion, plusieurs mécanismes peuvent accélérer les particules:
- Le champ électrique crée localement, parallèle au champ magnétique permet d'accélérer les particules. En présence d'un champ électrique, les particules chargées sont soumises à la force :
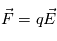 . D'après la relation fondamentale de la dynamique il est facile de montrer qu'un champ électrique uniforme parallèle au champ magnétique permet d'accélérer les particules chargées (voir exercice)
. D'après la relation fondamentale de la dynamique il est facile de montrer qu'un champ électrique uniforme parallèle au champ magnétique permet d'accélérer les particules chargées (voir exercice) - Les processus de résonnance entre les ondes et les particules permet de transférer l'énergie des ondes du milieu aux particules qui seront donc accélérées. Une particule entre en résonnance avec les ondes du milieu lorsque lorsque la vitesse de la particule est proche de la vitesse de résonnance qui dépend du type d'onde. Lorsque la particule intéragit avec un paquet d'onde, elle perd puis gragne successivement de l'énergie. Il faut donc un certains nombre d'intération pour avoir un changement. C'est une accélération stochastique. Lorsqu'une particule a une vitesse inférieur à la vitesse de résonnance, elle accélerera tandis qu'une partiucles plus rapide que la vitesse de résonnance déccélerera.
- Des chocs locaux générés par les nouvements de plasma en réponse au changement de connectivité du champ magnétique permet également d'accélérer les particules par un processus d'accélération de Fermi. En effet, nous avons vu à la page précédente que les vitesses d'éjection en sortie de la reconnexion pouvaitent attendre facilement des vitesse Alfvéniques, i.e., des vitesses supérieures à la vitesse de propagation de l'information dans le milieu. Le jet de reconnection et le plasma ambiant sont des milieux magnétisés. L'orientation du champ magnétique peut être différentes et eles particules pourront alors etre déflectées à chaque fois qu'elles changeront d'environnement magnétique. Ces milieux agiront comme des miroirs magnétiques. La particule qui traverse l'interface entre les 2 milieux magnétisé rencontre des champs magnétiques différents. La particules est alors déviées de sa trajectoire : elle est réfléchie. Tant que les milieu sont immobiles, il n'y a pas de gain réel d'énergie. Alors que si la particule arrive sur un milieu se déplacant à une vitesse vm , la nouvelle vitesse sera v+vm. Afin d'accélérer efficacement des particules, un nombre important d'aller retour est nécessaire entre les 2 milieux magnétisés.
Finalement, lors de leurs éjections, les CMEs peuvent atteindre des vitesses super-Alfvéniques (i.e., plus rapide que la vitesse d'Alfven qui est la vitesse charactéristique de propagation de l'information pour un plasma magnétisé). Dans cette situation, il y a formation d'un choc en amont de l'éjection de masse coronale. Les particules peuvent alors être accélérées au niveau du choc par un processus d'accélération de Fermi.
 Accélération de particules lors de la reconnexion magnétique
Accélération de particules lors de la reconnexion magnétique
Déterminer l'accélération des particuls soumises à un champ électrique E.
Les signatures radiatives d'une éruption
Les émissions UV
Les émissions UV
Le Soleil est observé dans quasi la totalité du spectre électromagnétique. Les températures atteintes lors des éruptions et la composition chimique de la couronne implique que les boucles post-éruptives et les rubans sont principalement observés dans le domaine Ultra-violet. Cela correspond notamment aux raies de transition atomique du Fer ionisé plusieurs fois et excité.
- Au niveau des sites d'impact chromosphériques du flux de chaleur, le milieu est exité localement. Les ions lourds sont alors éxités par collision entre eux et changent d'état d'énergie. Lors du refroidissement, ces éléments chromosphériques dépeuplent les niveaux d'énergie par désexitation radiative et émettent des photons (processus identique aux raies d'émission de l'hydrogène en Hα). Observationnellement on remarque la formation de ce que l'on appelle des rubans d'éruptions localisés aux pieds des boucles post-eruptives
- De plus le flux de chaleur va chauffer le plasma chromosphérique. Ce dernier, plus chaud, va se dilater et a remplir progressivement la boucle post-eruptive, c'est l'évaporation chromosphérique.
shema de l'evaporation chromospheric.
Comme ci-dessus, c'est en se refroidissant que les ions du plasma se désexitent et émettent des photons. On observe ainsi le plasma se refroidissant dans les boucles post-eruptives ce qui permet d'obtenir une informations sur la géométire des boucles après l'éruption
Films rubans et boucles post eruptives
En utilisant plusieurs filtres, on peut osberver les différentes raies. Chaque raies correspond à une transition atomique d'un élément à une température donnée. En combinant les différentes observations il est possible d'estimer le profil thermique des structures post-éruptives. Le plasma qui émet en UV est contenu dans les boucles magnétiques résultant de l'éruption. Les observations UV permettent ainsi d'observer l'évolution dynamique du champ magnétique durant l'éruption (cf films).
Le rayonnement X et
Le rayonnement
Les particules accélérées au site de reconnexion peuvent etre également observé indirectement en rayons X et γ. Apres avoir été accélérées, les particules vont suivre les lignes de champ magnétiques. En effet, même pour des particules très énergétiques, voire relativistes, le rayon de Larmor 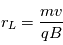 (q est la charge de la particules; m sa masse; v, sa vitesse et B, la magnitude du champ magnétique) est de l'ordre de quelques mètres à quelques kilomètres et est donc petit devant la taille des structures magnétiques coronales qui sont de l'ordre de 10 à 100 Mm.
(q est la charge de la particules; m sa masse; v, sa vitesse et B, la magnitude du champ magnétique) est de l'ordre de quelques mètres à quelques kilomètres et est donc petit devant la taille des structures magnétiques coronales qui sont de l'ordre de 10 à 100 Mm.
 Calcul du rayon de Larmor
Calcul du rayon de Larmor
Une particules chargée dans un champ magnétique est soumis à la force de Lorentz. cf ci-dessous
Question 1)
En utilisant la relation fondamentale de la dynamique, déterminer l'équation de la trajectoire d'une particule chargée q dans un champ B suivant la géométrie présenté sur la figure.
Question 2)
A partir de la solution périodique obtenue, retrouver l'expression du rayon de Larmor.
Parmis les particules accélérées, on trouve bien évidement les électrons. Lorsque les électrons pénètrent dans la couche chromosphérique plus dense, ils vont intéragir avec les ions du milieu ambiant. Comme pour toutes particules chargées, lorsque les électrons s'approchent trop pres d'un ion chargé positivement, il est soumis à la force electrostatique de l'ion. Cette interaction a pour resultat de dévier l'électron de sa trajetoire.
Figure de l'interaction electrons-protons et de l'emission d'un gamma
La modification de la trajectoire est équivalent à une décélération de la particules, ce qui équivaut à une perte d'énergie. Cette perte d'énergie se traduit alors par l'émission d'un photon. Lors des éruptions solaires, on mesure le rayonnement X dur entre 50 keV et 800 keV, correspondant à des photons émis par des électrons de 100keV à 1MeV.
Sur le meme modèle de rayonnement, on observe également des X-mou de 1keV à 20 keV. Ces X resultent du rayonnement de freinage du plasma thermique (distribution maxwellienne) chauffé au minimum à 7 MK.
Ces émissions en X sont détectées grace au satellite RHESSI et fournissent la meilleure indication que des electrons sont accélérées au site de reconnexion. Comme pour les rubans d'éruptions, les sources X et γ sont localisées au pieds des boucles post-éruptives et sont en générales superposabels aux rubans (cf Films).
Le rayonnement gamma
Comme pour les électrons, les ions sont accélérés à haute énergies et impactent la chromosphẻre, ils exitent les ions du milieu ambiant. Lorsque ces ions excités se désexitent, ils émettent un photon ainsi que des neutrons secondaires et des positrons. Pour les ions, la gamme de fréquence d'émission des photons est celle des rayons γ, plus énergétiques que les rayons X. D'autres émissions découlent de l'exitation des ions chromospheriques. Les neutrons secondaires peuvent etre recapturer par les protons du milieu ambiant, fromant du Deuterium. Lors de sa desexitation, ce deuterium émet un photon à 2,2 MeV. Les positrons quand à eux seront alors annihiler avec les électrons du milieu et l'énergie résultante est de 511 keV.
Tandis que le rayonnement X mettent en évidence que les électrons peuvent être accélérés jusqu'à plusieurs MeV au site de reconnexion, le rayonnement gamma montrent que les ions sont également accélérés à haute énergie. Comme pour les émissions UV, lorsque le signal est suffisant il est possible d'imager la source d'émission gamma. Bien que légèrement decallé par rapport aux X-durs, les sources gamma sont localisées au niveua des rubans d'éruption, i.e., au pieds des boucles post-eruptive.
Contrairement au rayonnement X, le rayonnement γ est de plus haute énergie et il n'y a actuellement aucun instrument dédié pour observer les γ d'origine solaire. Nous manquons donc ici d'observations pour tester directement les théories.
Le rayonnement radio
Emission synchrotron
En plus du rayonnement UV, X et γ, les phénomènes solaires émettent largement en onde radio. La gamme de longueur d'ondes des émission radio solaire s'étend de quelques dizaine de GHz dans la couronne solaire, ce sont les micro-ondes (domaine centimétriques), à quelques kHz (ondes kilométriques) au voisinage de la Terre. Les processus d'émission diffèrent en fonction du milieu et du phénomènes physique qui le crée.
Dans la couronne solaire les électrons énergétiques presque relativistes (100keV à qlqes MeV) émettent un rayonnement synchrotron. Ce rayonnement est généré par la giration des électrons dans un champ magnétique. Chaque électrons émet indépendamment des uns des autres, i.e., le rayonnement est incohérent et couvre une large gamme de fréquence. Etant donné l'intenisté du champ magnétique dans les région actives, qlqe centaine de Gauss, on considère que l'émission synchrotron est le mécanisme responsable des sources radio observés entre une centaine de MHz et qlqes GHz.
La fréquence à laquelle l'électron émet est la fréquence cyclotronique qui n'est autre que la fréquence de giration de l'életrons dans un champ B, i.e., 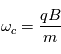 (cf calcul de la trajectoire d'une particules dans un champ B). En utilisant les valeur numérique pour la charge et la masse de l'électron, cette fréquence cyclotronique ne dépend plus que de la valeur du champ magnétique :
(cf calcul de la trajectoire d'une particules dans un champ B). En utilisant les valeur numérique pour la charge et la masse de l'électron, cette fréquence cyclotronique ne dépend plus que de la valeur du champ magnétique : ![\nu_{ce}=2.8\frac{B}{10^{-4}T}~[MHz]](../pages_etoile-planete/equations_rayonnement/equation4.png) .
.
D'après l'expression ci dessus, lorsque le champ magnétique diminue, la fréquence d'émission diminue également. Dans la couronne solaire, le champ magnétique devient de plus en plus faible avec l'altitude. On s'attend donc à observer une diminution de la fréquence d'émission au fur et à mesure que l'on s'éloigne du Soleil.
Figure : spectre dynamique avec une emission synchrotron et des type III.
Emission plasma cohérente
Après avoir été accélérés au site de reconnexion, les électrons précitent vers la surface solaire, mais peuvent également s'échapper vers l'espace interplanétaire le long de lignes de champ magnétiques ouvertes. La propagation de ces faisceau d'électrons énergétiques dans un plasma à plus basse température entraine la formation d'une instabilité plasma. Cette instabilité produit des ondes de langmuir qui sont émises à une fréquence proche de la fréquence plasma 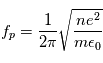 . Les ondes de Langmuir sont des ondes electrostatiques et ne se propagent donc pas seules. Ce n'est qu'après leur conversion en ondes électromagnétiques qu'elles pourront se propager et etre observer. La fréquence des ondes electromagnetiques est proche de cette fréquence plasma. Ce processus d'émission est dit cohérent puisque c'est processus du à une distribution et non à des particules individuelles.
. Les ondes de Langmuir sont des ondes electrostatiques et ne se propagent donc pas seules. Ce n'est qu'après leur conversion en ondes électromagnétiques qu'elles pourront se propager et etre observer. La fréquence des ondes electromagnetiques est proche de cette fréquence plasma. Ce processus d'émission est dit cohérent puisque c'est processus du à une distribution et non à des particules individuelles.
La fréquence plasma est proportionnelle à la densité du plasma ambiant. D'après les observations et en accord avec une atmosphère solaire hydrostatique, la densité de l'héliosphère décroit avec la distance au Soleil. Ainsi lorsqu'un faisceau d'électron se propage dans le milieu interplanétaire, la fréquence de l'emission radio decroit au fur et a mesure que le faisceau s'éloigne du Soleil. Les faisceau d'électrons étant rapide (proche de la vitesse de la lumière), la dérive de l'émission en temps et fréquence est rapide également. Sur les spectres dynamiques on n'observe quasiment pas de dérive en temps. On apelle ces emission radio des émission de type III
Un second phénomène solaire associé à une émission plasma cohérente du type instabilité faisceau plasma est le choc crée en amont des éjections de masse coronale. Au niveau du choc, des électrons sont accélérés générant localement des faisceaux d'électrons plus rapide que les électrons du milieu ambiant. Comme ci-dessus, cea entraine l'émission d'onde électrostatique à la fréquence plasma qui se recombinnent pour donner des ondes électromagnétiques. Les faisceaux d'électrons sont concentrés au niveau du choc de l'éjection de masse coronale, et c'est donc la vitesse de la CME qui défini la vitesse de propagation des faisceaux dans le milieu interplanétaire ou la densité decroit avec la distance au Soleil. Comme pour les typee III, la fréquence d'émission diminue avec le temps mais la vitesse de dérive plus lente que les type III. Ce sont des types II, signatures d'un choc crée par une CME.
 Calcul de la fréquence plasma
Calcul de la fréquence plasma
La fréquence plasma est la fréquence à laquelle oscille les électrons autour de leur état d'équilibre dans le champ électrique crée par les électrons du milieu ambiant.
Question 1)
A partir du théorème de Gauss : 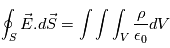 , calculer le champ électrique à travers une surface S, crée par une densité de charge
, calculer le champ électrique à travers une surface S, crée par une densité de charge 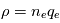 présente dans un volume V.
présente dans un volume V.
Question 2)
A partir de la relation fondamentale de la dynamique, déterminer la trajectoire d'un électrons soumis au champ électrique crée par les électrons du milieu.
 Les émissions radios solaires
Les émissions radios solaires
Question 1)
A partir des propriétés décrites dans le cours, identifiez sur les spectres présentés les émission radio du au rayonnement synchrotron.
Question 2)
En utilisant la formule , calculer la magnitude du champ magnétique minimum et maximum pour ces émissions synchrotron
Question 3)
En utilisant les propriétés des émissions plasma cohérente décrites dans le cours, identifiez sur le spectre les tye II et type III. Estimer leur vitesses de dérives.
Les relations Soleil-Planète
Le flux solaire
L'irradiance solaire
Impact sur le climat
Le champ magnétique interplanétaire
La spirale de Parker
Le champ magnétique interplanétaire
Nous avons vu précédemment que le champ magnétique solaire approche celui d'un dipole puis s'ouvre lorsque l'on s'éloigne du soleil à partir d'une distance appelé source surface, 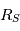 . Dans le milieu interplanétaire,
. Dans le milieu interplanétaire, 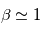 , i.e., le plasma du vent solaire impose son mouvement au champ magnétique. La forme du champ B interplanétaire est alors une combinaison entre le flot radial du plasma du vent solaire et d'un champ magnétique radial en rotation (On suppose les pieds du champ magnétique fixé à la surface du soleil).
, i.e., le plasma du vent solaire impose son mouvement au champ magnétique. La forme du champ B interplanétaire est alors une combinaison entre le flot radial du plasma du vent solaire et d'un champ magnétique radial en rotation (On suppose les pieds du champ magnétique fixé à la surface du soleil).
En supposant que le vent solaire et le champ magnéique s'étendent seulement en 2 dimension, on a : 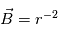 . En coordonnées sphériques, on suppose un champ magnétique à symétrie de révolution :
. En coordonnées sphériques, on suppose un champ magnétique à symétrie de révolution : 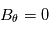 et azimuthale :
et azimuthale : 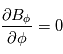 . On développe alors la condition
. On développe alors la condition 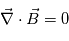 (équation de Maxwell), et on obtient :
(équation de Maxwell), et on obtient :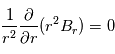 . En intégrant, on obtient entre la source surface et une distance
. En intégrant, on obtient entre la source surface et une distance 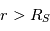 :
:
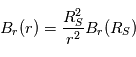 .
Si l'on suppose que la structure du milieu interplanétaire est stationnnaire,
.
Si l'on suppose que la structure du milieu interplanétaire est stationnnaire, 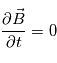 , on peut calculer
, on peut calculer 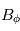 à partir de l'équation d'induction :
à partir de l'équation d'induction : 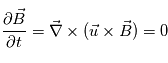 .
.
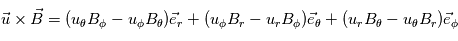
Le vent solaire et le champ magnétique s'étend en 2D, donc 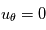 et
et 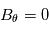
On se retrouve alors avec : 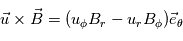
En utilisant l'expression du rotationel d'un vecteur et en ne gardant que les termes contenant la composante θ de ce vecteur, on obtient :
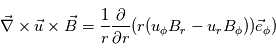
En intégrant de la surface source RS à une distance r, on obtient : 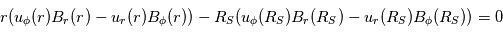 . A la surface source, B est radial, i.e.
. A la surface source, B est radial, i.e. 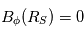 , et
, et 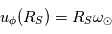 , où ω est la vitesse angulaire du Soleil.
, où ω est la vitesse angulaire du Soleil.
Finalement, 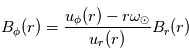 . Pour un distance r grande,
. Pour un distance r grande, 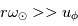 et
et 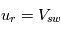 la vitesse du vent solaire, on a
la vitesse du vent solaire, on a 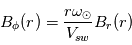 .
.
 Détermination de la Spirale de Parker
Détermination de la Spirale de Parker
Pour déterminer la forme du champ magnétique interplanétaire, il faut calculer les lignes de forces du champ, i.e, les lignes co-linéaire au champ magnétique en tout point : On peut alors montrer que les lignes de forces ont une forme de spirale d'archimède.
Une ligne de force est une courbe qui est tangente partout au champ magnétique, i.e., 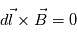
Question 1)
Déterminer l'équation des lignes de forces du champ magnétique interplanétaire.
Spirale de Parker
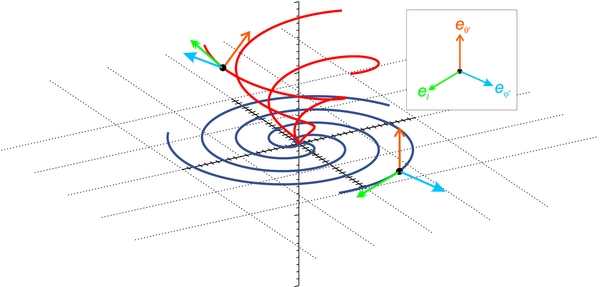
Les lignes bleues représentent la forme du champ magnétique interplanétaire au niveau du plan de l'écliptique, tandis que les rouges représente des lignes à plus hautes latitudes.
Crédit :
M. S. Marsh, S. Dalla, J. Kelly, and T. Laitinen, The Astrophysical Journal, Volume 774, Number 1
La connexion Soleil - planète
La connexion Soleil-planète
Dans le cadre des relations Soleil - planète, le champ magnétique interplanétaire a un rôle déterminant.
- C'est lui qui connecte magnetiquement le Soleil et les planètes. Lorsque des particules accélérées vont s'échapper vers l'espace interplanétaire, elle vont suivre les lignes du champ interplanétaire. Si les particules voyagent sur des lignes non-connecté à la Terre, elles ne l'impacteront pas. Cette notion est illustré sur le shéma.
- Lorsqu'une éjection de masse coronale se propage dans l'espace interplanétaire, elle interagit directement avec son milieu environnant, ce qui a pour effet de modifier son champ magnétique par erosion, son taux d'expansion en fonction de la pression exterieur, son accélération, i.e., son temps d'arrivée sur Terre
Dans une situation ou le milieu interplanétaire suit la spirale de Parker, on peut déterminer la région à la surface solaire ou doit avoir lieu une éruption pour que les particules atteignent la Terre. Dans le plan de l'ecliptique, on définit l''angle que fait la ligne de champ avec l'axe terre soleil tel que : 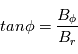 . D'après l'expression du champ magnétique interplanétaire, l'angle
. D'après l'expression du champ magnétique interplanétaire, l'angle 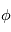 dépend de la vitesse du vent solaire et de la distance au Soleil A la Terre,
dépend de la vitesse du vent solaire et de la distance au Soleil A la Terre, 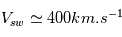 , et
, et 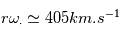 , ce qui donne
, ce qui donne 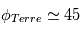 .
.
En utilisant les équations des lignes de champs, on peut alors calculer la position, 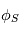 du pied de la ligne à la surface source. La vitesse andulaire du Soleil est
du pied de la ligne à la surface source. La vitesse andulaire du Soleil est 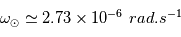 . A la Terre, on a
. A la Terre, on a 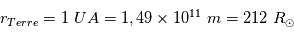 avec
avec 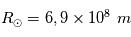 , et l'angle
, et l'angle 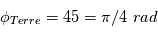 . Pour une surface source
. Pour une surface source 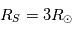 , on a :
, on a :
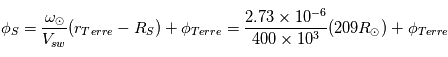
D'après le calcul ci-dessus, pour que les particules énergétiques arrivent à la Terre, l'éruption solaire devrait avoir lieu à proximité du pied de la spirale de Parker connectée à la Terre, c'est a dire à l'Ouest solaire autour de 45 degré.
Impact des éruptions solaires sur les environnements planétaires
Propagation des CMEs
Interaction CMEs planètes
Interaction CME-planètes
Les conséquences de l'interaction entre les CMEs et les environnements planétaires dépend fortement de la nature de l'environnement planétaire impliqué. Dans notre système solaire, on distingue 3 groupe d'environnements: Les planètes avec une atmosphère et une magnétosphère (ex: la Terre); les planètes avec une atmosphère et sans magnétosphère (Mars) et les planètes sans atmosphère et sans magnétosphère (La Lune).
L'interaction des CMEs avec des planètes à atmosphère et magnétosphère engendrent la formation d'aurores. Lorsque la CME impacte la magnétosphère, leur champ magnétique reconnecte l'un avec l'autre. Grace à ce couplage, les particules solaires contenues dans la CMEs sont transférés à la magnétopshère. Elles suivent le champ magnétopshérique et precipitent au pole magnétique de la planète pour ionisé les atomes ionosphériques. Lors de la recombinaison de ce atomes, des photons sont émis.
Dans le cas des planètes sans magnétosphère, il n y a pas de "bouclier magnétique" pour proteger l'environnement planétaire"l'impact des CME et meme du vent solaire
Propagation des particules énergétiques
Propagation des particules énergétiques
Réponses aux QCM
pages_interieur/convective.html
QCM
'QCM : Interieur solaire'
- Question 1
Solution : réponse 2)
- Question 2
Solution : réponse 2)
- Question 3
Solution : réponse 1)
- Question 4
Solution : réponse 3)
Réponses aux exercices
pages_etoile-planete/dipole.html
Exercice
'Détermination de la valeur du champ magnétique'
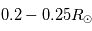 et contient 60% de masse solaire. C'est dans cette région où est produite la majorité de l'énergie solaire rayonnée par la surface. Cette énergie est générée par les réactions de fusion nucléaires de l'hydrogène. En effet, la compression gravitationnelle dans cette région est telle que la densité est de
et contient 60% de masse solaire. C'est dans cette région où est produite la majorité de l'énergie solaire rayonnée par la surface. Cette énergie est générée par les réactions de fusion nucléaires de l'hydrogène. En effet, la compression gravitationnelle dans cette région est telle que la densité est de 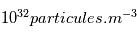 (la densité de l'atmosphère terrestre est de
(la densité de l'atmosphère terrestre est de 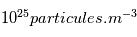 ) et la température atteint
) et la température atteint 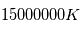 . Pour l'hydrogène, ces conditions impliquent que l'énergie cinétique du à lagitation thermiquedu plasma est supérieure à la repulsion coulombienne présente lorsque 2 particules de même charge se rapprochent.
. Pour l'hydrogène, ces conditions impliquent que l'énergie cinétique du à lagitation thermiquedu plasma est supérieure à la repulsion coulombienne présente lorsque 2 particules de même charge se rapprochent.
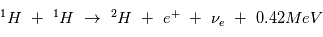
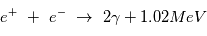
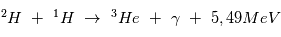
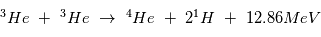
 Température de fusion au coeur du Soleil
Température de fusion au coeur du Soleil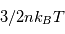 et l'energie coulombienne est
et l'energie coulombienne est 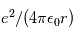 où r est la distance entre les deux noyau et doit etre inférieure à
où r est la distance entre les deux noyau et doit etre inférieure à 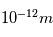 , e est la charge d'un électron en coulomb
, e est la charge d'un électron en coulomb 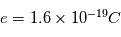 ,
, 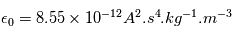 est la permettivité électrique du vide,
est la permettivité électrique du vide, 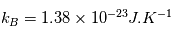 est la constante de Boltzmann.
est la constante de Boltzmann.
 Energie de la fusion thermonucléaire
Energie de la fusion thermonucléaire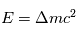 où m est la masse atomique en kg des éléments de la réaction,
où m est la masse atomique en kg des éléments de la réaction, 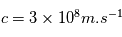 est la vitesse de la lumière et l'énergie E est en Joule.
est la vitesse de la lumière et l'énergie E est en Joule.
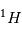 est formé d'un proton et d'un électron. Son isotope le Deuterium
est formé d'un proton et d'un électron. Son isotope le Deuterium 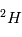 est consititué d'un proton, d'un neutron et d'un électron et le tritium
est consititué d'un proton, d'un neutron et d'un électron et le tritium 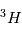 = 1 proton, 2 neutrons et 1 electron. La masse atomique de l'hydrogène est donc 1,0079u.
= 1 proton, 2 neutrons et 1 electron. La masse atomique de l'hydrogène est donc 1,0079u.
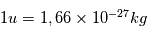 , calculez la masse atomique de 4 atomes d'hydrogène
, calculez la masse atomique de 4 atomes d'hydrogène 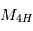 en kg?
en kg?
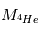 est 4.0026 u. En utilisant la relation masse-énergie d'einstein, calculer l'énergie libérée lors de la fusion de 4 atomes d'hydrogènes en un atome d'hélium.
est 4.0026 u. En utilisant la relation masse-énergie d'einstein, calculer l'énergie libérée lors de la fusion de 4 atomes d'hydrogènes en un atome d'hélium.
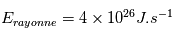 . Estimez alors le temps de vie du Soleil pour consommer tout son hydrogène.
. Estimez alors le temps de vie du Soleil pour consommer tout son hydrogène.
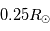 et
et 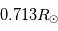 . C'est dans cette zone que l'énergie produite au coeur du soleil est transportée par rayonnement jusqu'à la zone convective. La densité et la température diminuent respectivement d'un facteur 1000 et 10 dans cette région. Les réactions de fusion ne sont alors plus possibles et les photons en provenance du coeur entrent en collision avec les particules du plasma ambient. Lors de ces collisions l'énergie du photon est absorbée par les particules, qui sont alors exitées. Lors de leur desexitation, un photon de plus faible énergie est émis. Le
. C'est dans cette zone que l'énergie produite au coeur du soleil est transportée par rayonnement jusqu'à la zone convective. La densité et la température diminuent respectivement d'un facteur 1000 et 10 dans cette région. Les réactions de fusion ne sont alors plus possibles et les photons en provenance du coeur entrent en collision avec les particules du plasma ambient. Lors de ces collisions l'énergie du photon est absorbée par les particules, qui sont alors exitées. Lors de leur desexitation, un photon de plus faible énergie est émis. Le
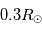 restant. Elle ne contient que 2% de la masse solaire et la température chute de
restant. Elle ne contient que 2% de la masse solaire et la température chute de 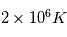 à
à 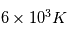 . Comme dans le cas d'une casserole d'eau bouillante, la chaleur est tranportée de la base de la zone convective à la surface solaire par le mécanisme de convection. En effet, lorsque la variation 'ou gradient' de température devient trop élevé, le rayonnement ne peut evacuer toute l'énergie et des régions vont être chauffées plus que d'autres. Ces zones plus chaudes vont alors se déplacer vers la surface sous l'effet de la poussée d'Archimède et engendrer ainsi des mouvements de matière déclenchant la convection.
Les cellules de convection sont d'ailleurs observables à la surface solaire dans la gamme visible des longueurs d'ondes. C'est la granulation, voir le film réalisé à partir des observation du pic du midi avec un filtre a
. Comme dans le cas d'une casserole d'eau bouillante, la chaleur est tranportée de la base de la zone convective à la surface solaire par le mécanisme de convection. En effet, lorsque la variation 'ou gradient' de température devient trop élevé, le rayonnement ne peut evacuer toute l'énergie et des régions vont être chauffées plus que d'autres. Ces zones plus chaudes vont alors se déplacer vers la surface sous l'effet de la poussée d'Archimède et engendrer ainsi des mouvements de matière déclenchant la convection.
Les cellules de convection sont d'ailleurs observables à la surface solaire dans la gamme visible des longueurs d'ondes. C'est la granulation, voir le film réalisé à partir des observation du pic du midi avec un filtre a 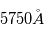 . La taille d'un granule est d'environ 1 Mm.
. La taille d'un granule est d'environ 1 Mm.


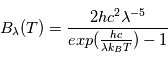
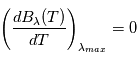 . On obtient alors la loi de Wien telle que:
. On obtient alors la loi de Wien telle que: 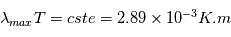
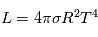 avec la constante de Stefan Boltzman
avec la constante de Stefan Boltzman ![\sigma = 5.67 \times 10^-8 [W.m^{-2}.K^{-4}]](../pages_etoile-planete/equations_atmosphere/equation5.png)
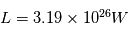 , estimez le rayon solaire.
, estimez le rayon solaire.
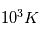 . Alors que la chute en densité avec l'altitude est attendue pour une atmosphère, l'augmentation de la température est toujours un domaine de recherche actif. La chromosphère étant plus ténue que la photosphère, l'approximation du corps noir n'est plus valide, c'est alors les interactions photon-matière qui dominent l'émission.
. Alors que la chute en densité avec l'altitude est attendue pour une atmosphère, l'augmentation de la température est toujours un domaine de recherche actif. La chromosphère étant plus ténue que la photosphère, l'approximation du corps noir n'est plus valide, c'est alors les interactions photon-matière qui dominent l'émission.
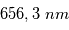 qui correspond à la raie
qui correspond à la raie 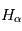 de l'hydrogène. Pour déterminer les longueurs d'ondes des raies atomiques de l'hydrogène, on utilise le modèle atomique de Bohr. Un atome d'hydrogène est composé d'un électron en orbite autour du noyau. Cet électron peut se trouver sur différentes orbites en fonction de l'énergie du système. L'un des postulats de Bohr est la quantification du moment cinétique, et donc que l'énergie totale de l'électron sur une orbite donnée est aussi quantifiée. On peut en effet montrer que l'énergie totale d'un électron est :
de l'hydrogène. Pour déterminer les longueurs d'ondes des raies atomiques de l'hydrogène, on utilise le modèle atomique de Bohr. Un atome d'hydrogène est composé d'un électron en orbite autour du noyau. Cet électron peut se trouver sur différentes orbites en fonction de l'énergie du système. L'un des postulats de Bohr est la quantification du moment cinétique, et donc que l'énergie totale de l'électron sur une orbite donnée est aussi quantifiée. On peut en effet montrer que l'énergie totale d'un électron est :
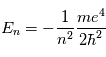
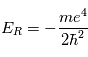 est l'énergie de Rydberg et correspond à l'état d'énergie le plus bas pour n=1. Pour déterminer l'énergie du photon émis/absorbé pour passer d'un niveau
est l'énergie de Rydberg et correspond à l'état d'énergie le plus bas pour n=1. Pour déterminer l'énergie du photon émis/absorbé pour passer d'un niveau 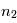 à
à 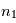 , il suffit de calculer la différence d'énergie entre les 2 niveaux :
, il suffit de calculer la différence d'énergie entre les 2 niveaux : 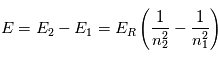
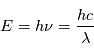
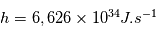 est la constante de Planck,
est la constante de Planck, 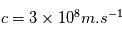 est la vitesse de la lumière,
est la vitesse de la lumière, 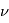 et
et 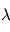 sont respectivement la fréquence et la longueur d'onde du photon émis ou absorbé. En égalisant les 2 expressions définissant l'énergie d'un photon, on obtient une expression pour déterminer la longueur d'onde du photon émis :
sont respectivement la fréquence et la longueur d'onde du photon émis ou absorbé. En égalisant les 2 expressions définissant l'énergie d'un photon, on obtient une expression pour déterminer la longueur d'onde du photon émis : 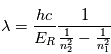
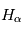 . C'est le cas par exemple des protubérances solaires. Ces structures seront présentées plus en détails dans la partie activité solaire.
. C'est le cas par exemple des protubérances solaires. Ces structures seront présentées plus en détails dans la partie activité solaire.

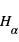 de l'hydrogène. A gauche : Les taches blanches correspondent à des région en émission alors que les structures filamentaires en noire correspondent à l'absorption. Les structures noires sont des filaments, l'équivalent des protubérance que l'on observe au limbe solaire vue sur l'image de droite).
de l'hydrogène. A gauche : Les taches blanches correspondent à des région en émission alors que les structures filamentaires en noire correspondent à l'absorption. Les structures noires sont des filaments, l'équivalent des protubérance que l'on observe au limbe solaire vue sur l'image de droite).
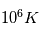 . Elle s'étend de la chromosphère à environ quelques rayons solaires. Au dela de la couronne s'étend le milieu interplanétaire ou héliosphère qui englobe tout notre système solaire jusqu'à l'héliopause, interface avec le milieu interstellaire.
. Elle s'étend de la chromosphère à environ quelques rayons solaires. Au dela de la couronne s'étend le milieu interplanétaire ou héliosphère qui englobe tout notre système solaire jusqu'à l'héliopause, interface avec le milieu interstellaire.
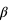 du plasma qui donne le rapport entre la pression cinétique,
du plasma qui donne le rapport entre la pression cinétique, 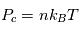 , et la pression magnétique,
, et la pression magnétique, 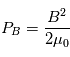 , tel que :
, tel que :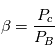 . Lorsque le champ magnétique domine,
. Lorsque le champ magnétique domine, 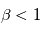 , c'est le cas de la couronne et lorsque le plasma domine
, c'est le cas de la couronne et lorsque le plasma domine 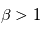 , c'est le cas de la photosphère.
, c'est le cas de la photosphère.


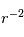 causé par le champ de gravité de l'étoile elle-même. En résolvant les équations de l'hydrodynamique on trouve une infinité de solution. L'unique solution stable est celle où la vitesse du fluide augmente jusqu'a atteindre la vitesse du son (= vitesse caractéristique de la propagation de l'information dans un fluide), c'est la solution trans-sonique. Dans le cas d'une atmosphère magnétisée comme la couronne solaire, ce sont les équations de la magnétohydrodynamique (ou MHD) qu'il faut résoudre. On peut alors montrer numériquement que la solution stable est la solution trans-alfvènique (= vitesse caractéristique de la propagation de l'information dans un plasma magnétisé).
causé par le champ de gravité de l'étoile elle-même. En résolvant les équations de l'hydrodynamique on trouve une infinité de solution. L'unique solution stable est celle où la vitesse du fluide augmente jusqu'a atteindre la vitesse du son (= vitesse caractéristique de la propagation de l'information dans un fluide), c'est la solution trans-sonique. Dans le cas d'une atmosphère magnétisée comme la couronne solaire, ce sont les équations de la magnétohydrodynamique (ou MHD) qu'il faut résoudre. On peut alors montrer numériquement que la solution stable est la solution trans-alfvènique (= vitesse caractéristique de la propagation de l'information dans un plasma magnétisé).


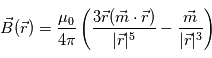 . En coordonnées cylindrique on définit
. En coordonnées cylindrique on définit 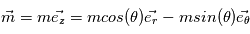 et
et 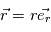 comme illustré sur le shéma ci-contre (haut).
En développant cette expression, on obtient :
comme illustré sur le shéma ci-contre (haut).
En développant cette expression, on obtient : 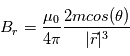 et
et 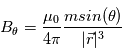 . On ontient une solution paramétrique en fonction de r et
. On ontient une solution paramétrique en fonction de r et 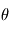 . En calculant les lignes de forces telle que, en tout point, une ligne de force est colinéaire au champ B, i.e.,
. En calculant les lignes de forces telle que, en tout point, une ligne de force est colinéaire au champ B, i.e., 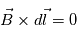 , on obtient un champ B dans l'espace
, on obtient un champ B dans l'espace 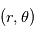 .
.


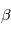 du plasma augmente pour atteindre des valeurs
du plasma augmente pour atteindre des valeurs 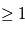 . La pression dynamique du plasma est alors la variable dominante. Le vent solaire étant majoritairement un flot radial de plasma, ceci a pour conséquence d'étendre les lignes de champ magnétique jusqu'au limite de l'héliosphère. Le champ magnétique coronal à grande échelle est alors défini par l'équilibre entre la pression dynamique du plasma et la tension magnétique du champ dipolaire.
. La pression dynamique du plasma est alors la variable dominante. Le vent solaire étant majoritairement un flot radial de plasma, ceci a pour conséquence d'étendre les lignes de champ magnétique jusqu'au limite de l'héliosphère. Le champ magnétique coronal à grande échelle est alors défini par l'équilibre entre la pression dynamique du plasma et la tension magnétique du champ dipolaire.


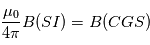
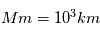 pour les petites régions actives à quelques centaines de Mm pour les plus imposantes. Ces régions actives se forment par le processus d'émergence de flux magnétique de l'interieur solaire vers l'atmosphere. Mais comment passe-t-on d'un champ magnétique dipolaire à un champ mutli-polaire en surface ?
pour les petites régions actives à quelques centaines de Mm pour les plus imposantes. Ces régions actives se forment par le processus d'émergence de flux magnétique de l'interieur solaire vers l'atmosphere. Mais comment passe-t-on d'un champ magnétique dipolaire à un champ mutli-polaire en surface ?

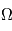 , le vecteur champ magnetique sort de la surface à un pied et 'replonge' dans le soleil à son autre pieds. Cela se traduit par l'apparition d'un bipole magnetique dont les 2 polarités, positive (blanc sur la figure) et négative (en noir sur la figure), correspondent aux deux pieds des boucles magnétiques formées par le tube du flux qui a émergé.
, le vecteur champ magnetique sort de la surface à un pied et 'replonge' dans le soleil à son autre pieds. Cela se traduit par l'apparition d'un bipole magnetique dont les 2 polarités, positive (blanc sur la figure) et négative (en noir sur la figure), correspondent aux deux pieds des boucles magnétiques formées par le tube du flux qui a émergé.




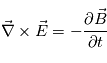 , en utilisant l'équation de Maxwell
, en utilisant l'équation de Maxwell 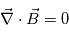 et la loi d'Ohm non généralisé :
et la loi d'Ohm non généralisé : 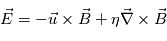 , on obtient l'expression de l'équation d'induction :
, on obtient l'expression de l'équation d'induction : 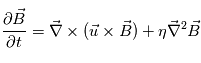 . Avec
. Avec 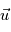 la vitesse du plasma et
la vitesse du plasma et 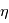 la resistivité électrique du milieu. Le premier terme est le terme d'advection et le second terme est le terme dissipatif.
la resistivité électrique du milieu. Le premier terme est le terme d'advection et le second terme est le terme dissipatif.
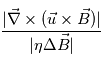 . La couronne solaire étant un très bon conducteur, la resistivité électrique
. La couronne solaire étant un très bon conducteur, la resistivité électrique 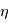 est petite et le reynolds magnétique est alors >> 1 : le terme d'avection domine. La reconnexion magnétique se développe lorsque le terme dissipatif est du même ordre de grandeur que le terme d'advection du champ magnétique. En explicitant le nombre de Reynolds on obtient :
est petite et le reynolds magnétique est alors >> 1 : le terme d'avection domine. La reconnexion magnétique se développe lorsque le terme dissipatif est du même ordre de grandeur que le terme d'advection du champ magnétique. En explicitant le nombre de Reynolds on obtient : 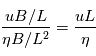 . u est la vitesse caracteristique du plasma , L la longueur caracteristique de la region de dissipation et
. u est la vitesse caracteristique du plasma , L la longueur caracteristique de la region de dissipation et 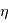 la resistivité électrique du milieu. Si L devient très petit, le terme d'advection diminue et devient comparable au terme dissipatif. Dans la couronne solaire, le mécanisme de reconnexion magnétique se developpera aux petites échelles (L petit).
la resistivité électrique du milieu. Si L devient très petit, le terme d'advection diminue et devient comparable au terme dissipatif. Dans la couronne solaire, le mécanisme de reconnexion magnétique se developpera aux petites échelles (L petit).
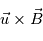 exprime le champ életrique crée par les déplacements du plasma magnétisé à une vitesse u. On peut montrer que le champ électrique parallele ne provient que du rotationnel du champ magnétique. La création d'un champ électrique s'accompagne de la formation d'une nappe de courant (loi de Maxwell-Ampère :
exprime le champ életrique crée par les déplacements du plasma magnétisé à une vitesse u. On peut montrer que le champ électrique parallele ne provient que du rotationnel du champ magnétique. La création d'un champ électrique s'accompagne de la formation d'une nappe de courant (loi de Maxwell-Ampère : 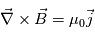 ).
).

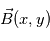 distribué comme le montre le schéma (a ajouter)en coordonnées cartesienne. On suppose alors aucun mouvement de plasma, i.e.,
distribué comme le montre le schéma (a ajouter)en coordonnées cartesienne. On suppose alors aucun mouvement de plasma, i.e., 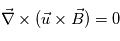 . L'équation d'induction est alors réduite à
. L'équation d'induction est alors réduite à 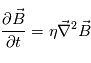 .
Expliciter cette equation pour le champ magnetique donne ci-dessus :
.
Expliciter cette equation pour le champ magnetique donne ci-dessus :
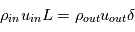 .
.
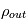 et
et 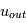 , la densité et la vitesse de sortie du fluide par le coté
, la densité et la vitesse de sortie du fluide par le coté 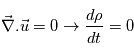 , soit
, soit 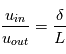
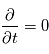 . L'équation d'induction devient alors
. L'équation d'induction devient alors 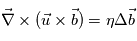 .
Le rapport du terme d'advection et du terme diffusif défini le nombre de Reynolds magnétique. Ce nombre défini le régime physique dans lequel se trouve le système. Pour que la reconnexion ait lieu il faut que le terme diffusif soit du même ordre de grandeur que le terme d'advection, i.e., Rm ~1. En estimant ce nombre de Reynolds à partir des grandeur caractéristique du système, i.e. les différentielles spatiales sont proportionnelles à l'inverse de la longueur caractéristique du système, on obtient :
.
Le rapport du terme d'advection et du terme diffusif défini le nombre de Reynolds magnétique. Ce nombre défini le régime physique dans lequel se trouve le système. Pour que la reconnexion ait lieu il faut que le terme diffusif soit du même ordre de grandeur que le terme d'advection, i.e., Rm ~1. En estimant ce nombre de Reynolds à partir des grandeur caractéristique du système, i.e. les différentielles spatiales sont proportionnelles à l'inverse de la longueur caractéristique du système, on obtient :
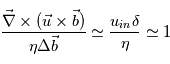
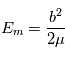 ) est transformée en énergie cinétique, on a :
) est transformée en énergie cinétique, on a : 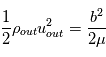 .
Donc
.
Donc 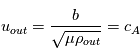 . La vitesse du fluide en sortie de la nappe de courant n'est autre que la vitesse d'Alfvèn. L'éjection de matière accompagnant la reconnexion magnétique est un mouvement Alfvénique. Au site de reconnexion dans la couronne, le champ magmétique est de l'ordre de 500 à 1000 G et la densité est de l'ordre de 108-9 g.cm-3 . La perméabilité magnétique dans la couronne approche celle du vide (
. La vitesse du fluide en sortie de la nappe de courant n'est autre que la vitesse d'Alfvèn. L'éjection de matière accompagnant la reconnexion magnétique est un mouvement Alfvénique. Au site de reconnexion dans la couronne, le champ magmétique est de l'ordre de 500 à 1000 G et la densité est de l'ordre de 108-9 g.cm-3 . La perméabilité magnétique dans la couronne approche celle du vide (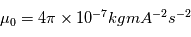 ). On a donc une vitesse d'Alfvèn comprise entre 1000 et 5000 km.s-1. En comparaison avec les vitesses typique de la photosphère de l'ordre de quelques dizaines de km.s-1, le jet de matière en sortie de la nappe de courant est très rapide.
). On a donc une vitesse d'Alfvèn comprise entre 1000 et 5000 km.s-1. En comparaison avec les vitesses typique de la photosphère de l'ordre de quelques dizaines de km.s-1, le jet de matière en sortie de la nappe de courant est très rapide.
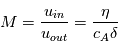 . Pour une vitesse d'Alfvèn et une resistivité
. Pour une vitesse d'Alfvèn et une resistivité 
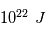 , et ont un impact non négligeables sur les environnement planétaires.
, et ont un impact non négligeables sur les environnement planétaires.
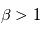 , i.e., les mouvements photospheriques du plasma déplacent les tubes de flux magnétiques émergés dans la couronne. En réponse à ces mouvements photosphériques, le filament s'élève tout d'abord lentement, puis est soudainement éjecté dans l'atmosphère solaire à des vitesses pouvant atteindre plusieurs milliers de km. s-1. C'est une éjection de masse coronale qui va par la suite se propager dans le milieu interplanétaire et le modifier.
, i.e., les mouvements photospheriques du plasma déplacent les tubes de flux magnétiques émergés dans la couronne. En réponse à ces mouvements photosphériques, le filament s'élève tout d'abord lentement, puis est soudainement éjecté dans l'atmosphère solaire à des vitesses pouvant atteindre plusieurs milliers de km. s-1. C'est une éjection de masse coronale qui va par la suite se propager dans le milieu interplanétaire et le modifier.
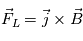 . Cette force peut s'exprimer en fonction de 2 composantes. Sachant que
. Cette force peut s'exprimer en fonction de 2 composantes. Sachant que 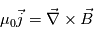 (Equation d'Ampère),
(Equation d'Ampère), 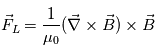 . En utilisant les identité vectorielles, on peut décomposer la force de Lorentz telle que :
. En utilisant les identité vectorielles, on peut décomposer la force de Lorentz telle que : 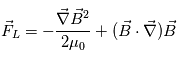 . Le premier terme correspond à la pression magnétique et le deuxieme à la tension magnétique.
. Le premier terme correspond à la pression magnétique et le deuxieme à la tension magnétique.


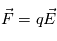 . D'après la relation fondamentale de la dynamique il est facile de montrer qu'un champ électrique uniforme parallèle au champ magnétique permet d'accélérer les particules chargées (voir exercice)
. D'après la relation fondamentale de la dynamique il est facile de montrer qu'un champ électrique uniforme parallèle au champ magnétique permet d'accélérer les particules chargées (voir exercice) 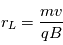 (q est la charge de la particules; m sa masse; v, sa vitesse et B, la magnitude du champ magnétique) est de l'ordre de quelques mètres à quelques kilomètres et est donc petit devant la taille des structures magnétiques coronales qui sont de l'ordre de 10 à 100 Mm.
(q est la charge de la particules; m sa masse; v, sa vitesse et B, la magnitude du champ magnétique) est de l'ordre de quelques mètres à quelques kilomètres et est donc petit devant la taille des structures magnétiques coronales qui sont de l'ordre de 10 à 100 Mm.
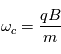 (cf calcul de la trajectoire d'une particules dans un champ B). En utilisant les valeur numérique pour la charge et la masse de l'électron, cette fréquence cyclotronique ne dépend plus que de la valeur du champ magnétique :
(cf calcul de la trajectoire d'une particules dans un champ B). En utilisant les valeur numérique pour la charge et la masse de l'électron, cette fréquence cyclotronique ne dépend plus que de la valeur du champ magnétique : ![\nu_{ce}=2.8\frac{B}{10^{-4}T}~[MHz]](../pages_etoile-planete/equations_rayonnement/equation4.png) .
.
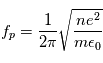 . Les ondes de Langmuir sont des ondes electrostatiques et ne se propagent donc pas seules. Ce n'est qu'après leur conversion en ondes électromagnétiques qu'elles pourront se propager et etre observer. La fréquence des ondes electromagnetiques est proche de cette fréquence plasma. Ce processus d'émission est dit cohérent puisque c'est processus du à une distribution et non à des particules individuelles.
. Les ondes de Langmuir sont des ondes electrostatiques et ne se propagent donc pas seules. Ce n'est qu'après leur conversion en ondes électromagnétiques qu'elles pourront se propager et etre observer. La fréquence des ondes electromagnetiques est proche de cette fréquence plasma. Ce processus d'émission est dit cohérent puisque c'est processus du à une distribution et non à des particules individuelles.
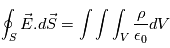 , calculer le champ électrique à travers une surface S, crée par une densité de charge
, calculer le champ électrique à travers une surface S, crée par une densité de charge 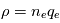 présente dans un volume V.
présente dans un volume V.
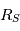 . Dans le milieu interplanétaire,
. Dans le milieu interplanétaire, 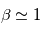 , i.e., le plasma du vent solaire impose son mouvement au champ magnétique. La forme du champ B interplanétaire est alors une combinaison entre le flot radial du plasma du vent solaire et d'un champ magnétique radial en rotation (On suppose les pieds du champ magnétique fixé à la surface du soleil).
, i.e., le plasma du vent solaire impose son mouvement au champ magnétique. La forme du champ B interplanétaire est alors une combinaison entre le flot radial du plasma du vent solaire et d'un champ magnétique radial en rotation (On suppose les pieds du champ magnétique fixé à la surface du soleil).
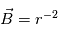 . En coordonnées sphériques, on suppose un champ magnétique à symétrie de révolution :
. En coordonnées sphériques, on suppose un champ magnétique à symétrie de révolution : 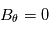 et azimuthale :
et azimuthale : 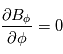 . On développe alors la condition
. On développe alors la condition 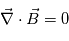 (équation de Maxwell), et on obtient :
(équation de Maxwell), et on obtient :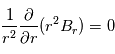 . En intégrant, on obtient entre la source surface et une distance
. En intégrant, on obtient entre la source surface et une distance 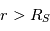 :
:
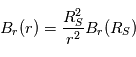 .
Si l'on suppose que la structure du milieu interplanétaire est stationnnaire,
.
Si l'on suppose que la structure du milieu interplanétaire est stationnnaire, 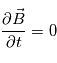 , on peut calculer
, on peut calculer 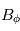 à partir de l'équation d'induction :
à partir de l'équation d'induction : 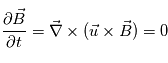 .
.
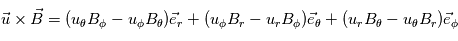
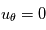 et
et 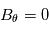
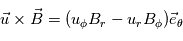
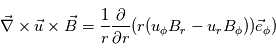
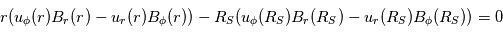 . A la surface source, B est radial, i.e.
. A la surface source, B est radial, i.e. 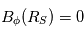 , et
, et 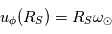 , où
, où 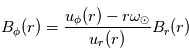 . Pour un distance r grande,
. Pour un distance r grande, 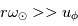 et
et 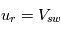 la vitesse du vent solaire, on a
la vitesse du vent solaire, on a 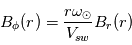 .
.
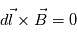

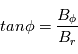 . D'après l'expression du champ magnétique interplanétaire, l'angle
. D'après l'expression du champ magnétique interplanétaire, l'angle 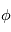 dépend de la vitesse du vent solaire et de la distance au Soleil A la Terre,
dépend de la vitesse du vent solaire et de la distance au Soleil A la Terre, 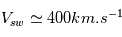 , et
, et 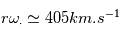 , ce qui donne
, ce qui donne 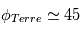 .
.
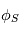 du pied de la ligne à la surface source. La vitesse andulaire du Soleil est
du pied de la ligne à la surface source. La vitesse andulaire du Soleil est 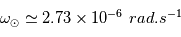 . A la Terre, on a
. A la Terre, on a 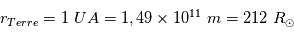 avec
avec 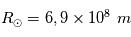 , et l'angle
, et l'angle 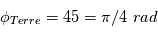 . Pour une surface source
. Pour une surface source 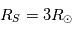 , on a :
, on a :