Processus stochastique et Densité spectrale de puissance

Auteur: Nathan Hara & Jacques Laskar

Processus stochastique

La notion de densité spectrale de puissance (DSP) n'est pas simple à définir, cependant très utilisée dans la littérature de traitement du signal. Nous donnons une définition mathématique pour qu'il n'y ait pas d'ambiguités mais compte tenu de la sophistication des notions introduites, le lecteur pourra se référer à la description qualitative suivante.

La densité spectrale de puissance est une propriété relative à plusieurs variables aléatoires. Les familles de variables aléatoires peuvent par exemple représenter des mesures sur lesquelles on a une incertitude. A chaque instant de mesure on associe une variable alétoire qui a une certaine densité de probabilité. En physique théorique ou en économie, on rencontre des processus stochastiques continus - typiquement le mouvement brownien, qui représente des mouvements d'atomes ou des fluctuations de prix. Formellement, un processus stochastique est une famille de variables aléatoires indexées par un ensemble totalement ordonné 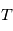, toutes définies sur le même espace de probabilité ( 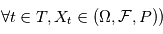$\forall t \in T, X_t \in (\Omega,\mathcal{F},\mathbb{P}) )$ . 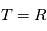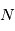Dans ce cours on aura seulement besoin de $T=\mathbb{R}$ ou $\mathbb{N}$ . 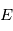On note $\mathbb{E}$ l'espérance mathématique.

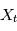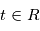Dans le cas général, la densité de probabilité de la variable aléatoire $X_{t}$ (pour $t \in \mathbb{R}$ ) dépend des valeurs prises à d'autres "instants" par les autres variables aléatoires. En particulier on peut s'intéresser à une éventuelle probabilité de périodicité. Par exemple si on modélise un nombre de ventes de vêtement par jour, on verra des ventes plus importantes au moment des soldes (à peu près tous les six mois). La densité spectrale de puissance est un outil qui permet de visualiser ce genre de périodicité. 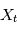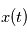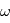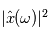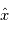Dans la section suivante, on voit que si on prend une famille de variables aléatoires certaines, c'est à dire que X_t vaut une certaine valeur réelle x(t) avec la probabilité 1, la DSP en une fréquence $\omega$ est égale à $|\hat{x}(\omega)|^2$ , où $\hat{x}$ est la transformée de Fourier de 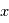. Si maintenant 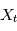X_t est une variable alétoire, la DSP sera la "transformée de Fourier typique" d'une réalisation de X_t .

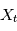Pour définir cette notion mathématiquement, on doit d'abord introduire les notions de convergences et intégrales en moyenne quadratique. Pour plus de précision le lecteur peut se référer au cours de Timo Koski à KTH.

Intégrale en moyenne quadratique (Mean Square Integral)

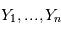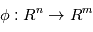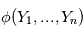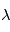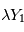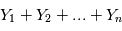Rappelons d'abord que si Y_1, ..., Y_n sont des variables aléatoires et $\phi: \mathbb{R}^n\rightarrow \mathbb{R}^m$ une fonction mesurable alors $\phi(Y_1,...,Y_n)$ est une variable aléatoire. En particulier, si $\lambda$ est un scalaire, $\lambda Y_1$ et Y_1 + Y_2 +...+Y_n sont des variables aléatoires. Pour un rappel sur les variables aléatoires, voir le cours de Didier Pelat.

Soit 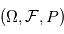$(\Omega,\mathcal{F},\mathbb{P})$ un espace de probabilités, on dit que la suite de variables aléatoires 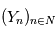$(Y_n)_{n \in \mathbb{N}}$ telle que 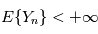$E\{Y_n\} < + \infty$ , définies sur cet espace converge en moyenne quadratique si et seulement si:

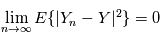
$\lim\limits_{n \rightarrow \infty} \mathbb{E}\{|Y_n-Y |^2\}=0$

Soit 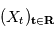$(X_t)_{\mathbf{t \in \mathbb{R}}}$ un processus stochastique continu ( 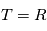$T=\mathbb{R}$ ) tel que chacune des variables aléatoires 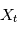X_t a une espérance finie ( 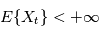$E\{X_t\} < + \infty$ ). L'intégrale en moyenne quadratique du processus 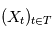$(X_t)_{t \in T}$ sur l'intervalle [a,b] est définie comme la limite en moyenne quadratique (lorsqu'elle existe) de:

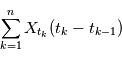
$\sum\limits_{k=1}^n X_{t_k} (t_k-t_{k-1}})$

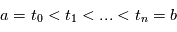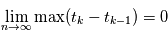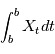Pour a=t_0 < t_1 <... <t_n=b et $\lim\limts_{n\rightarrow\infty}\max (t_k-t_{k-1}) = 0$ . On la note alors $\int_b^b X_t dt$ .

On définit alors la densité spectrale de puissance comme:

$P_X(\omega) = \lim\limits_{T\rightarrow \infty} \mathbb{E} \{|\hat{x}_T(\omega)|^2\}$

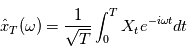
Où $\hat{x}_T(\omega) = \frac{1}{\sqrt{T}} \int_0^T X_t e^{-i \omega t} dt$

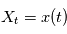Cette définition un peu complexe peut être vue comme une généralisation de la transformée de Fourier à des processus stochastiques. En effet, lorsque le processus X_t est telle que X_t = x(t) avec une probabilité 1, l'intégrale en moyenne quadratique se comporte comme l'intérale de Riemann, alors 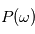$P(\omega)$ est le carré du module de la transformée de Fourier de la fonction réelle d'une variable réelle 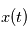x(t) . Dans le cas où les 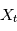X_t sont aléatoire, 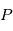est le carré de la transformée de Fourier "en moyenne" des réalisations de 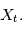X_t. 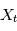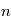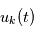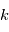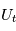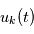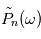Par exemple si X_t modélise une tension mesurée au cours du temps dans une expérience d'électronique réalisée un grand nombre de fois, donnant profils de tension u_k(t) à l'expérience (des réalisations du processus stochastique U_t ), la moyenne des carrés du module des transformées de Fourier des u_k(t) notée $\tilde{P}_n(\omega)$ sera approximativement égal à 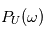$P_U(\omega)$ . Si le nombre d'expérience 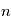tend vers l'infini 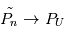$\tilde{P_n} \rightarrow P_U$ en norme 2.

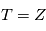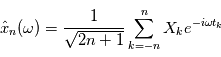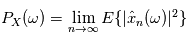Dans le cas d'un processus stationnaire discret ( $T= \mathbb{Z}$ ), on peut directement définir $\hat{x}_n(\omega)=\frac{1}{\sqrt{2n+1}} \sum\limits_{k=-n}^n X_ke^{-i\omega t_k}$ et $P_X(\omega) = \lim\limits_{n\rightarrow \infty} \mathbb{E} \{|\hat{x}_n(\omega)|^2\}$ .

Processus stationnaires au sens large

La densité spectrale de puissance a une définition plus simple lorsque le processus est stationnaire, c'est à dire lorsque le processus 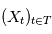$(X_t)_{t\in T}$ vérifié:

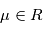Il existe $\mu \in \mathbb{R}$ tel que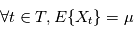 $\forall t \in T, \mathbb{E}\{X_t\} =\mu$
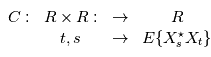La fonction d'autocorrélation $\begin{array}{cccc}C: &\mathbb{R} \times \mathbb{R}: & \rightarrow & \mathbb{R} \\ &t,s & \rightarrow& \mathbb{E}\{X^{\star}_s X_t \} \end{array}$ ne dépend que de 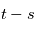, i. e. 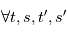$\forall t,s, t',s'$ tels que 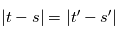, on a 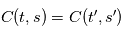. On note appelle alors habituellement la fonction d'autocorrélation 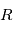, telle que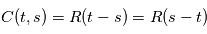

Les processus stationnaires modélisent des phénomènes qui ont une certaine invariance dans le temps, en particulier la covariance ne dépend pas de 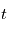de manière absolue, mais de manière relative à un autre instant. Dans ce cas, la densité spectrale de puissance est égale au carré du module de la transformée de Fourier de la fonction 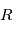. L'équivalence avec la définition de la densité spectrale de puissance donnée plus haut est établie par le théorème de Wiener-Khinchin.