Combien d'exoplanètes dans la Voie Lactée ?
La première question concerne le nombre d'exoplanètes dans les sytèmes planétaires de notre galaxie, la Voie Lactée, en comparaison des planètes du système solaire. Notez que jusqu'à ce jour, on ne détecte que les exoplanètes de la Voie Lactée. On ne sait rien des planètes des milliards d'autres galaxies connues.
Supposons que la Voie Lactée soit constituée de 100 milliards d'étoiles, ce qui est juste au première ordre. Supposons aussi que la probabilité de trouver des planètes autour d'une étoile soit la même pour chaque étoile. Ceci est sûrement faux mais simplifie les calculs. Enfin supposons que la loi de probabilité du nombre de planètes par étoile est une loi de Poisson ayant un paramètre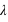 
égal à 5.
Combien en moyenne y a-t-il d'exoplanètes autour des étoiles ? Quelle est la probabilité de trouver un système planétaire avec un nombre égal à la moyenne ?
Quel est la probabilité de trouver un système planétaire tel que le système solaire, avec huit planètes ou avec au moins huit planètes ? Que conclure sur le système solaire dans ce cas ?
Considérant les données observationnelles, la plupart des exoplanètes sont seules autour de leur étoile. Dans ce cas, la loi des grands nombres tendrait à montrer que la moyenne des exoplanètes par étoiles serait proche de 1. Que devient la chance de trouver un système solaire dans un tel cas. Quelle est l'erreur de raisonnement fait ici ?
Combien statistiquement devrait-il y avoir d'exoplanètes dans la Voie Lactée ?
Les Jupiter Chauds
Cet exercice porte sur les Jupiter Chauds, des exoplanètes ayant une masse similaire à celle de Jupiter et très proches de leur étoile. Outre leur intérêt physique qui obligent à repenser la formation et l'évolution des planètes, ces planètes sont aussi intéressantes d'un point de vue statistique, car elles sont plus faciles à détecter et donc moins sujettes aux biais observationnels. Cet exercice montre que même avec une faible fraction de Jupiter Chauds dans la galaxie, cette population peut paraître la plus importante avec des moyens obervationnels limités.
Supposons toujours que les étoiles ont toute la même loi de probabilité d'avoir des planètes, un loi de Poisson avec une moyenne de 5. Supposons que la probabilité pour une planète d'être un Jupiter Chaud soit de 0,0001. Supposons que l'on soit sûr de pouvoir les découvrir à une distance de 2 kpc. On suppose aussi que la probabilité qu'une planète soit de type Terre est de 0,1 mais qu'il n'est possible de la trouver qu'à moins de 50 parsec.
Quelle loi de probabilité va servir pour déterminer le nombre de Jupiter Chauds ou de planètes de type Terre par la suite?
Combien de Jupiter Chauds et de planètes de type Terre y aurait-il dans la Voie Lactée ? Quel est leur rapport ?
En sélectionnant 100 000 étoiles brillantes dans le ciel, toutes à moins de 2 kpc, dont 27 sont à moins de 50 parsec, combien statistiquement y aura-t-il de Jupiter Chauds et de planètes de type Terre découverts? Quel est leur rapport ? Conclure.
Relation étoiles-exoplanètes
Cet exercice s'intéresse aux relations qui pourraient exister entre les exoplanètes et leur étoile hôte. La théorie bayésienne est alors utilisée. Dans un vision plus réaliste des exoplanètes que pour les exercices précédents, la probabilité de présence de planètes n'est pas la même pour les différents types d'étoiles.
Lors d'une observation non biaisée, c'est à dire complète, pour détecter des planètes géantes gazeuses sur 200 étoiles, 28 planètes géantes gazeuses sont découvertes autour de 75 étoiles de métallicité plus grande que 0 (étoiles riches en métaux) et seulement 2 pour les 125 étoiles de métallicité plus petite que 0 (étoiles pauvres en métaux). A chaque fois, les planètes gazeuses géantes sont trouvées seules sans autre géante gazeuse. Que dire qualitativement de l'influence de la métallicité sur la détection de planètes gazeuses?
Soit, G, l'ensemble des étoiles ayant la propriété suivante "avoir une seule planète gazeuse pour une étoile" et son contraire NG ainsi que l'ensemble M ="avoir une étoile riche en métaux" et son contraire NM. Avec les données de l'énoncé, quelles sont les probabilités de P(G), P(NG), P(M), P(NM) ?
Que signifient les probabilité suivantes P(G|M) et P(G|NM) ? Quelles sont leurs valeurs ? Les comparer à P(G) et commenter.
Pour une étoile choisie au hasard, une unique planète géante gazeuse est observée. Qu'elle est la probabilité pour l'étoile d'être une étoile riche en métaux, P(M|G) ? Commenter.
Comparer la probabilité que l'étoile avait d'être riche en métaux avant et après la découverte de la planète géante gazeuse. Quels sont les points forts et les points faibles de cette méthode pour connaître la métallicité d'une étoile ?
Détection d'une exoplanète par transit
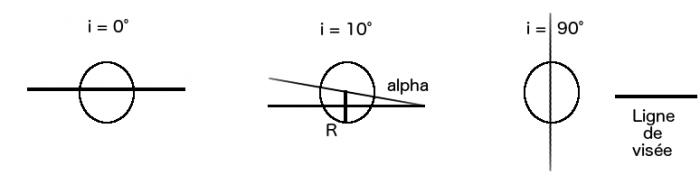
Lors d'un transit, une exoplanète passe devant son étoile depuis un observateur sur terre, la luminosité de l'étoile est alors diminuée durant un certain laps de temps avant de revenir à la normale. Cette mesure permet la détection d'une exoplanète. Lorsqu'une exoplanète est recherchée par la méthode des transits, les observateurs espèrent que cette l'orbite de l'exoplanète passe devant l'étoile hôte pour un observateur terrestre. Il y a un facteur chance pour détecter des transits d'une étoile donnée. Les campagnes de recherche observent un grand nombre d'étoiles et l'analyse des données nécessite de corriger le taux de détection de transits de la probabilité d'observer ces transits.
Supposons qu'une étoile ait un rayon de 1 million de km (par comparaison le Soleil fait près de 700 000 km de rayon), quel angle maximal, sur le plan d'une trajectoire circulaire d'une exoplanète à 1 U.A., faut-il pour voir un transit? Notons qu' une inclinaison de 0 degré signifie que la trajectoire est vue de côté, donc qu'il y a un transit, et qu'une inclinaison de 90 degrés signifie que la trajectoire est vue de face, donc sans transit.
Que dire sur l'influence du rayon de l'étoile et de la distance de l'exoplanète à cette étoile sur l'angle minimal requis pour détecter l'exoplanète ? Commenter le biais de cette méthode.
Que se passe-t-il qualitativement si l'orbite n'est plus circulaire mais elliptique ? Commenter sur un autre biais de la méthode des transits.
Dans le cas précédent (une exoplanète à 1 U.A. d'une étoile de rayon 1 millions de km), quelle est la probabilité de la détecter, sachant qu'aucun angle n'est a priori préféré pour son orbite circulaire ?
Que devient cette probabilité pour un Jupiter Chaud (distant de son étoile de 0.1 U.A) autour d'une étoile géante ayant un rayon de 10 millions de km ?