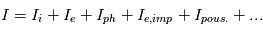Quelques généralités sur le principe d'une sonde électrostatique
Quelques généralités sur le principe d'une sonde électrostatique
Les sondes électrostatiques utilisées pour les missions spatiales sont basées sur des techniques de laboratoire développées et présentées par Irving Langmuir et ses collègues au milieu des années 1920. Ce n'est seulement qu'à partir de la fin des années 1950 que ce type de technique a été utilisé sur des fusées et satellites pour mesurer la densité des ions et des électrons ionosphériques, la température électronique et le potentiel du satellite.
La technique des sondes de Langmuir consiste à mesurer le courant collecté par la sonde lorsque l'on fait varier la tension apliquéee à celle-ci. Une sonde électrostatique est une électrode conductrice de taille et forme appropriées qui est insérée dans le plasma (pour les plamas spatiaux la sonde se trouve sur au bout d'un mât du satellite). La tension sur l'électrode varie par rapport à une électrode de référence et le courant collecté est mesuré. L'analyse de la réponse ''tension-courant (U-I)'', appelé caractéristique va permettre de déterminer les propriétés du plasma : sa densité électronique 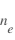 , sa température électronique
, sa température électronique 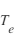 , la masse moyenne des ions
, la masse moyenne des ions 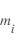 et la densité des ions
et la densité des ions 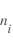 , ainsi que le potentiel du satellite.
, ainsi que le potentiel du satellite.
Une théorie simple de la sonde de Langmuir [Mott-Smith and Langmuir, 1926] montre que l'amplitude du courant électronique 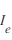 , est proportionnel à
, est proportionnel à 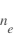 , et que l'amplitude du courant ionique
, et que l'amplitude du courant ionique 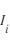 est proportionnel à
est proportionnel à 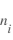 . Le courant pour des potentiels répulsifs est proportionnel à l'exponentielle de la tension divisée par la température :
. Le courant pour des potentiels répulsifs est proportionnel à l'exponentielle de la tension divisée par la température : 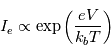
On fait varier le potentiel appliqué à la sonde 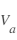 par rapport au satellite et on collecte le courant sur la sonde. Le courant
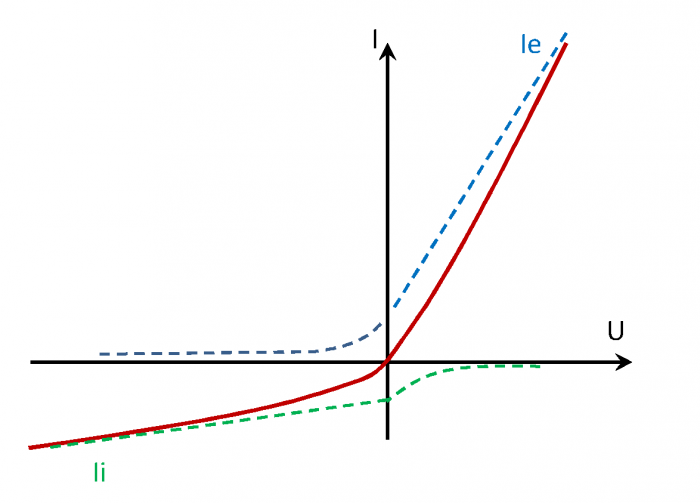
par rapport au satellite et on collecte le courant sur la sonde. Le courant 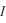 est la somme des courant ionique et électronique générés par les particules impactant la sonde. La figure de cette page illustre une représentation schématique d'un courant collecté par une sonde de Langmuir sphérique (celle de Cassini). Il est possible d'identifier différentes régions. Lorsque
est la somme des courant ionique et électronique générés par les particules impactant la sonde. La figure de cette page illustre une représentation schématique d'un courant collecté par une sonde de Langmuir sphérique (celle de Cassini). Il est possible d'identifier différentes régions. Lorsque 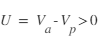 (
(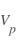 étant le potentiel du plasma) les électrons sont accélérés et les ions sont freinés. Dans le cas inverse (
étant le potentiel du plasma) les électrons sont accélérés et les ions sont freinés. Dans le cas inverse (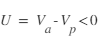 ) les électrons sont repoussés et les ions accélérés.
L'échantillonnage de la fonction de distribution des électrons en fonction du potentiel appliqué à la sonde est schématisé grâce à l'appliquette disponible à la page suivante.
) les électrons sont repoussés et les ions accélérés.
L'échantillonnage de la fonction de distribution des électrons en fonction du potentiel appliqué à la sonde est schématisé grâce à l'appliquette disponible à la page suivante.
Cette technique est une mesure active, c'est-à-dire qu'elle pertube le milieu qu'elle mesure. Ainsi l'insertion de la sonde va modifier le plasma. Lorsque la sonde n'est pas présente le plasma a localement une densité 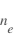 , une température
, une température 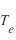 , une densité
, une densité 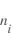 ,...
Lorsque la sonde est présente, la tension appliquée à la sonde va collecter les courants liés aux déplacement des charges électriques (ions et électrons). Du fait de la plus grande mobilité des électrons (moins massifs que les ions), les électrons vont impacter la sonde plus rapidement ce qui va créer une structure de potentiel autour de la sonde. Du coup un électron qui se trouve loin de la sonde et de sa structure de potentiel verra un potentiel différent que celui appliqué à la sonde à cause de cet écrantage. Cette région s'appelle la gaine et l'équilibre de charge entre ions et électrons est brisé.
,...
Lorsque la sonde est présente, la tension appliquée à la sonde va collecter les courants liés aux déplacement des charges électriques (ions et électrons). Du fait de la plus grande mobilité des électrons (moins massifs que les ions), les électrons vont impacter la sonde plus rapidement ce qui va créer une structure de potentiel autour de la sonde. Du coup un électron qui se trouve loin de la sonde et de sa structure de potentiel verra un potentiel différent que celui appliqué à la sonde à cause de cet écrantage. Cette région s'appelle la gaine et l'équilibre de charge entre ions et électrons est brisé.
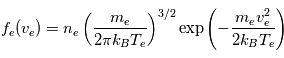
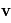 et
et 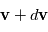 est ainsi égal à :
est ainsi égal à :
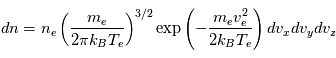
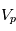 . On notera la tension
. On notera la tension 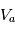 appliquée à la sonde, et
appliquée à la sonde, et 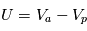 cette même tension mesurée par rapport au potentiel plasma.
cette même tension mesurée par rapport au potentiel plasma.
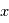 est normal au plan de la sonde. Les calculs dans le cas d'une géométrie sphérique sont proposés en exercice. On notera
est normal au plan de la sonde. Les calculs dans le cas d'une géométrie sphérique sont proposés en exercice. On notera 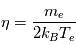
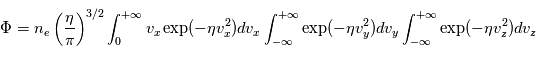
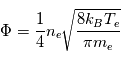
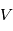 négatif (
négatif (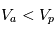 ), seuls les électrons ayant une vitesse telle que :
), seuls les électrons ayant une vitesse telle que :
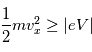 seront collectés, par contre tous les ions sont collectés.
seront collectés, par contre tous les ions sont collectés.
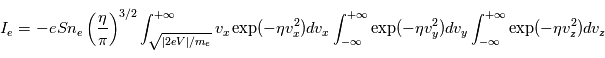 Ici,
Ici, 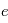 est la valeur absolue de la charge unitaire et
est la valeur absolue de la charge unitaire et 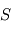 la surface de la sonde.
la surface de la sonde.
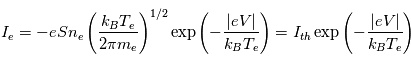 où
où 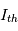 est le courant lié aux vitesses thermiques des particules. Le courant électronique est négatif à cause de la charge de l'électron.
est le courant lié aux vitesses thermiques des particules. Le courant électronique est négatif à cause de la charge de l'électron.
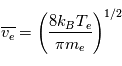 Le courant électronique s'écrit donc également :
Le courant électronique s'écrit donc également :
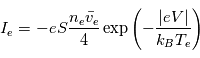
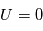 (i.e. une tension sonde égale au potentiel plasma) tous les électrons sont collectés. Pour
(i.e. une tension sonde égale au potentiel plasma) tous les électrons sont collectés. Pour 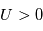 (c'est-à-dire
(c'est-à-dire 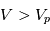 ), le courant est le même car tous les électrons sont collectés. Le courant électronique est alors constant et égal à :
), le courant est le même car tous les électrons sont collectés. Le courant électronique est alors constant et égal à :
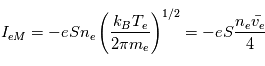 On montre alors que pour
On montre alors que pour 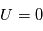 ,
, 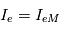 .
.
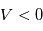 , tous les ions sont collectés et on devrait obtenir un courant ionique de saturation constant égal à :
, tous les ions sont collectés et on devrait obtenir un courant ionique de saturation constant égal à :
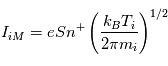
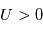 , les ions sont repoussés et seuls ceux dont la vitesse
, les ions sont repoussés et seuls ceux dont la vitesse 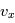 est suffisante pourront être collectés comme on l'a montré pour les électrons.
est suffisante pourront être collectés comme on l'a montré pour les électrons.
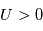 et tous les ions si
et tous les ions si 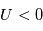 . Afin de conserver la neutralité
électrique du plasma il se crée, au voisinage de la sonde, une charge d'espace appelée ''gaine''. Les particules de même polarité que le potentiel de la surface sont exclues de cette gaine. Cette gaine est électronique si
. Afin de conserver la neutralité
électrique du plasma il se crée, au voisinage de la sonde, une charge d'espace appelée ''gaine''. Les particules de même polarité que le potentiel de la surface sont exclues de cette gaine. Cette gaine est électronique si 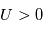 (afin de limiter le flux d'électrons) et ionique si
(afin de limiter le flux d'électrons) et ionique si 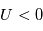 (pour limiter le flux d'ions). L'épaisseur de cette gaine est de l'ordre de grandeur de la longueur de Debye :
(pour limiter le flux d'ions). L'épaisseur de cette gaine est de l'ordre de grandeur de la longueur de Debye :
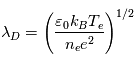
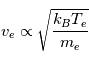 est beaucoup plus grande que la vitesse thermique des ions
est beaucoup plus grande que la vitesse thermique des ions 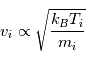 , et de ce fait plus d'électrons viennent frapper l'obstacle. Comme cet objet se charge négativement, les électrons sont repoussés. L'équilibre s'obtient lorsque le courant électronique collecté à la surface de l'objet (la sonde) vient équilibrer le courant ionique incident ce qui se produit pour une certaine valeur de potentiel que l'on appelle le potentiel flottant.
, et de ce fait plus d'électrons viennent frapper l'obstacle. Comme cet objet se charge négativement, les électrons sont repoussés. L'équilibre s'obtient lorsque le courant électronique collecté à la surface de l'objet (la sonde) vient équilibrer le courant ionique incident ce qui se produit pour une certaine valeur de potentiel que l'on appelle le potentiel flottant.
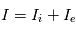 . Les paramètres plasmas
. Les paramètres plasmas 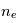 et
et 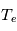 sont déterminés à partir du courant électronique
sont déterminés à partir du courant électronique 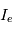 . Pour avoir accès au courant électronique, il faut éliminer la contribution du courant ionique du courant total mesuré. La
. Pour avoir accès au courant électronique, il faut éliminer la contribution du courant ionique du courant total mesuré. La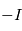 en fonction de
en fonction de 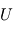 .
.
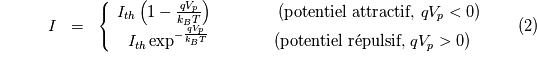
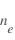 ,
, 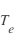 ...) à spécifier par l'utilisateur.
...) à spécifier par l'utilisateur.