Exoplanètes : Statistique et probabilités
Auteur: Sylvain Fouquet
- Statistique des exoplanètes
- Introduction
- L'échantillon statistique
- Représentativité d'un échantillon
- Extremum, médiane, quartile
- La boîte à moustaches
- Moyenne et écart-type
- Histogrammes
- Fonctions de distribution
- Statistique multidimensionnelle
- Statistique sur les étoiles hôtes I
- Statistique sur les étoiles hôtes II
- Signal sur Bruit
- Courbe transit
- Probabilités
- Probabilités
- Les variables aléatoires
- La fonction de probabilité
- Probabilité sur des sous-ensembles d'événements
- Calcul de la fonction de probabilité
- Introduction aux théorème de Bayes - Découvrir la bonne urne
- Théorème de Bayes
- Grandeurs classiques en probabilité
- Fonctions de distribution
- Loi binomiale
- La loi de Poisson
- La loi normale
- Exercices
- Variables aléatoires
- Ensemble
- Probabilités à variables discrètes et équipartition
- Probabilités conditionnelles
- Fonction de distribution
- Propriétés et applications de la loi binomiale
- Propriétés et applications de la loi poissonnienne
- Propriétés et applications de la Gaussienne
- Mini-projet
- Conclusion
-
Exoplanètes : Statistique et probabilités
Dans la recherche des exoplanètes, une question passionne les astrophysiciens et bien plus encore le reste de l'humanité : y a-t-il de la vie sur une autre planète ? La Terre prouve qu'un certain type de vie basée principalement sur le carbone peut exister. Reste à savoir si les processus ayant permis l'émergence de cette vie sur la Terre ont pu se produire sur une autre planète. La question de la vie extraterrestre ne se pose pas en terme de possibilité mais en terme de sa probabilité, de sa fréquence d'apparition.
La première partie de ce cours utilise les propriétés des exoplanètes pour faire découvrir la statistique, cet outil mathématique indispensable dans les sciences et en particulier en astronomie. La seconde partie du cours généralise et clarifie les notions mathématiques importantes du point de vue des probabilités. La troisième partie met à disposition des séries d'exercices pour tester les connaissances. Enfin la dernière partie est un test des connaissances mêlant statistiques et probabilités, mêlant cours et observations.
Dans la première partie des cours, des valeurs statistiques concernant la population des exoplanètes sont données pour illustrer les concepts présentés. Le nombre d'exoplanètes augmentant très rapidement, les paramètres statistiques évoluent aussi. Les valeurs actualisées peuvent être calculées à partir du catalogue.
Ce cours s'adresse à des étudiants de niveau L1 et plus. Il ne requiert aucune connaissance sur les probabilités ou la statistique.
Statistique des exoplanètes
Auteur: Sylvain Fouquet
Introduction
Planètes du système solaire
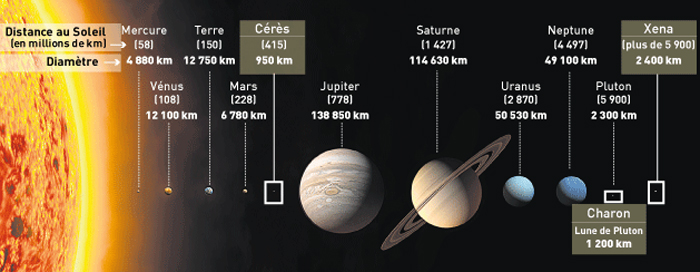
Planètes et planètes naines (encadrées sur fond marron) découvertes dans le système solaire.
Crédit :
http://mash.wifeo.com/astronomie.php
Cette première partie du cours s'intéresse à la statistique à travers le cas particulier des exoplanètes. Cet outil mathématique sert à extraire de l'information de grands échantillons de mesures. Les concepts statistiques décrits ici pour les exoplanètes sont généralisables dans d'autres cas. La statistique découle naturellement de questions scientifiques telles que "combien y a-t-il de planètes dans notre galaxie ?" ou encore "quelles masses ont elles ?" ou "quelles sont leurs distances à leurs étoiles hôtes ?". Ces questions sont déterminantes pour comprendre la formation et l'évolution des planètes et pour aider à la recherche d'une vie extraterrestre.
Avant les années 90, la connaissance sur les planètes se limitait aux neuf planètes du système solaire, Mercure, Vénus, la Terre, Mars, Jupiter, Saturne, Uranus, Neptune, Pluton. L'étude des exoplanètes n'existait pas faute d'observation. Il semblait cependant probable que d'autres planètes existaient autour d'autres étoiles que le Soleil, la formation d'une planète ne semblant pas un mécanisme requérant des conditions très spécifiques. Bien qu'Aleksander Wolszczan ait découvert des exoplanètes en septembre 1990 avec le radiotélescope Arecibo autour du pulsar PSR B1257+12 (une étoile en fin de vie, très dense avec une rotation très rapide), la science des exoplanètes a réellement débuté en 1995 avec la découverte de "51 Pegasi b" autour d'une étoile de type solaire par Michel Mayor et Didier Queloz. Plus de dix ans après, près de deux milles exoplanètes ont été découvertes et ce chiffre ne cesse de croître.
En plus des planètes du système solaire, des planètes naines ont été découvertes telles que Cérès. Pluton fut rétrogradée de son rang de planète pour devenir une planète naine.
Avec près de 2000 exoplanètes, des études statistiques permettent de découvrir des propriétés statistiques contraignant les modèles de formation et d'évolution des planètes. Le diagramme de Hubble pour les galaxies et le diagramme Hertzsprung-Russell pour les étoiles sont autant d'outils statistiques fondamentaux pour l'étude des galaxies et des étoiles.
Différentes propriétés sont mesurables pour chaque exoplanète : la masse, le rayon, le type spectral de l'étoile hôte, ... Cette première partie du cours utilise ces grandeurs pour caractériser les exoplanètes et en même temps pour introduire des concepts de statistique qui seront repris d'un point de vue probabiliste dans la seconde partie du cours.
L'échantillon statistique
Définition
Les études statistiques portent sur l'étude d'un échantillon de mesures. Cet échantillon est un ensemble de résultats, de nombres, acquis soit par la répétition d'une même expérience soit par la collection d'observations faites sur le même sujet. Par exemple, le résultat de dix lancers d'un dé, ou de dix dés lancers une fois, forme un échantillon de l'expérience "lancer de dé". Je peux faire la même chose avec des pièces ou des cartes. Moins classique, le résultat d'une pêche peut être vu comme un échantillon statistique des poissons se trouvant là où est le pêcheur. De ce dernier ensemble, la taille des poissons, leurs poids, etc, peuvent être étudiés. Un échantillon se caractérise par son nombre d'éléments. Plus un échantillon est grand, plus son étude est riche et précise.
L'échantillon des exoplanètes
Dans l'étude des exoplanètes, il s'agit de regarder un phénomène qui s'est répété : la formation d'exoplanètes. L'échantillon est donc constitué des exoplanètes découvertes. Actuellement l'échantillon d'exoplanètes connues comporte 1951 (au 8 septembre 2015) exoplanètes situées dans 1235 systèmes exoplanétaires. En effet, certains systèmes planétaires ont plusieurs exoplanètes. Les données utilisées dans ce cours sont fournies par la page internet exoplanet.eu/catalog. De cet échantillon d'exoplanètes, il est possible d'extraire différents échantillons, celui de des masses, des rayons, des eccentricités, etc, puis de les étudier.
Représentativité d'un échantillon
En statistique, le premier souci est la représentativité d'un échantillon. Pour bien comprendre la notion de représentativité, les sondages politiques sont pédagogiques. Durant une élection, un sondage doit donner approximativement le pourcentage de votes qu'obtiendra chaque candidat. Pour ce faire, un échantillon, de 1000 français par exemple, est sondé sur leurs futurs votes. Les sondeurs peuvent alors tirer des conclusions sur l'issue probable du résultat en faisant l'hypothèse que les 60 millions de français vont se comporter comme ces 1000 personnes. Dans ce cas, l'échantillon de 1000 personnes est dit représentatif de la totalité des français. L'échantillon peut cependants être biaisé si le sondeur ne sélectionne que des personnes ayant la carte du premier parti de droite ou bien des personnes lisant uniquement la presse dite de gauche. Il faut donc veiller à corriger le biais s'il est bien connu.
L'obtention d'un échantillon représentatif, sans biais, est une chose facile en théorie mais difficile en pratique. En théorie, il suffit de sélectionner un échantillon de manière aléatoire. Pour les élections, il suffit de tirer un certain nombre de français au hasard. Pour les exoplanètes, cette méthode est impossible pour la simple raison que toutes les exoplanètes de notre galaxie ne sont pas encore connues. Il existe en effet plusieurs biais qui font que certaines exoplanètes peuvent être surreprésentées par rapport à d'autres. Par exemple, les planètes très massives avec un grand rayon et très proches de leurs étoiles auront tendance à être plus facilement détectables et donc à être surreprésentées par rapport aux planètes de type terrestre qui sont petites, peu massives et loin de leurs étoiles hôtes. Toute étude statistique doit alors bien identifier ses biais afin de ne pas tirer de fausses conclusions. Un échantillon d'exoplanètes peut être complet jusqu'à une certaine limite de masse, de taille, de distance au soleil mais pas au-delà. Le travail du statisticien est de trouver cette limite pour tirer des conclusions non biaisées.
Extremum, médiane, quartile
Dans cette section du cours, nous illustrons les principales valeurs statistiques en utilisant la variable "masse" des exoplanètes.
La boîte à moustaches
Boîte à moustaches
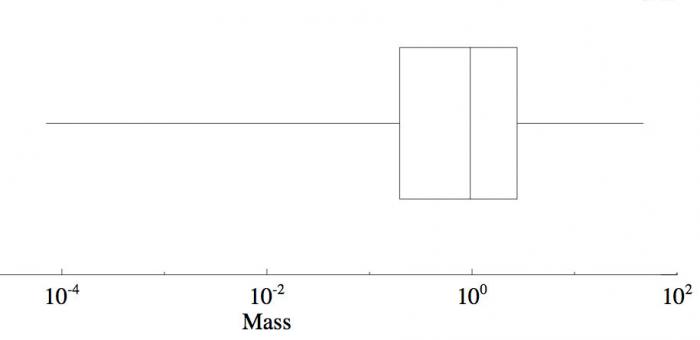
Boîte à moustaches schématisant la distribution des masses des 1032 exoplanètes de l'échantillon. L'axe horizontal représente les masses en échelle logarithmique. Ce schéma résume les cinq valeurs statistiques de la distribution de masse des exoplanètes qui sont par ordre croissant : le minimum (à gauche), le premier quartile (la côté gauche du rectangle), la médiane (le trait au centre du rectangle), le troisième quartile (le côté droit du rectangle) et le maximum (à droite).
Crédit :
Sylvain Fouquet
Boîte à moustaches
Toutes les informations statistiques décrites précédemment peuvent être résumées graphiquement par un schéma appelé la boîte à moustaches. Ce schéma montre les extrema reliés aux quartiles par des segments de droite (les moustaches) et les quartiles reliés à la médiane par des rectangles. La figure ci-dessus illustre une boîte à moustaches dans le cas des masses des exoplanètes. Cette visualisation graphique permet de décrire rapidement comment sont réparties les valeurs. Si les moustaches sont très grandes, cela signifie que les valeurs sont concentrées autour de la médiane. Au contraire, des rectangles de grande taille montrent une distribution dispersée.
Dans le cas de la masse des exoplanètes,cl'écart interquartile, c'est à dire l'écart entre le 1er quartile (0,197 MJ) et le 3ème quartile (2,75 MJ), est de 2,553 MJ.
La dispersion des masses des exoplanètes ne semble pas étendue, mais rappelons que, comme l'échantillon est biaisé vers les grandes masses, ce résultat est sûrement à revoir.
Moyenne et écart-type
Histogrammes
Histogrammes des masses
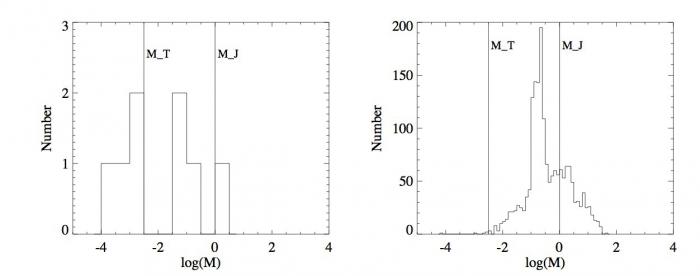
Histogrammes des masses des planètes du système solaire (gauche) et des exoplanètes (droite). L'échelle des masses est en échelle logarithmique par soucis de clarté.
Crédit :
Sylvain Fouquet
Histogramme
Les outils statistiques précédents sont pertinents lorsqu'il s'agit de distributions centrées autour d'une valeur. Dans le cas des planètes du système solaire, les masses sont soit petites (de l'ordre de la masse de la Terre), soit plus massives (de l'ordre de la masse de Jupiter). Cette distribution des masses, en plus d'autres propriétés physiques telles que la taille et la composition chimique, est à la base de la distinction entre les planètes gazeuses et les planètes telluriques.
Calculer la moyenne ou faire une boîte à moustache de l'échantillon des masses des planètes du système solaire ne permet pas de faire la distinction entre planètes telluriques et gazeuses.
Pour avoir une idée plus juste de la répartition des valeurs d'un échantillon, l'histogramme est un outil statistique plus approprié. Il requiert de calculer le nombre d'éléments de l'échantillon inclus dans des intervalles réguliers entre les extrema. L'avantage de l'histogramme est qu'il présente une vision claire de la distribution de notre échantillon. Mais si une taille des intervalles : 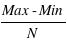 est trop petite, il n'y aura qu'un ou bien zéro élément de l'échantillon dans chaque intervalle. A l'inverse si les intervalles sont trop grands, il ne sera plus possible de distinguer les pics dans la distribution. Un bon choix pour le nombre d'intervalles est important. Si, par exemple, on divise le nombre total d'éléments de l'échantillon par N = 10, et que la distribution est uniforme, chaque intervalle devrait avoir à peu près 10 représentants.
est trop petite, il n'y aura qu'un ou bien zéro élément de l'échantillon dans chaque intervalle. A l'inverse si les intervalles sont trop grands, il ne sera plus possible de distinguer les pics dans la distribution. Un bon choix pour le nombre d'intervalles est important. Si, par exemple, on divise le nombre total d'éléments de l'échantillon par N = 10, et que la distribution est uniforme, chaque intervalle devrait avoir à peu près 10 représentants.
Dans le cas du système solaire, la figure de gauche montre qu'il y a deux pics dans la distribution des masses des planètes autour des masses 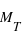 , la masse de la Terre, et
, la masse de la Terre, et 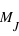 , la masse de Jupiter. L'histogramme des masses donne donc plus d'information que simplement une valeur centrale et une dispersion autour de cette valeur. Dans le cas de l'échantillon de toutes les masses connues des exoplanètes (figure de droite), l'histogramme montre que la répartition des exoplanètes a un pic aux alentours de
, la masse de Jupiter. L'histogramme des masses donne donc plus d'information que simplement une valeur centrale et une dispersion autour de cette valeur. Dans le cas de l'échantillon de toutes les masses connues des exoplanètes (figure de droite), l'histogramme montre que la répartition des exoplanètes a un pic aux alentours de 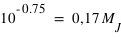 . De plus, le nombre d'exoplanètes avoisinant la masse de la Terre semble très faible. Encore une fois, cette propriété provient très probablement du biais observationnel qui privilégie les planètes massives et ne signifie en aucun cas que les planètes telluriques sont rares.
. De plus, le nombre d'exoplanètes avoisinant la masse de la Terre semble très faible. Encore une fois, cette propriété provient très probablement du biais observationnel qui privilégie les planètes massives et ne signifie en aucun cas que les planètes telluriques sont rares.
Fonctions de distribution
Fonctions de distributions des masses
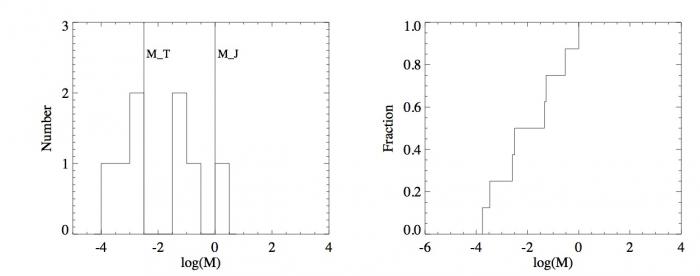
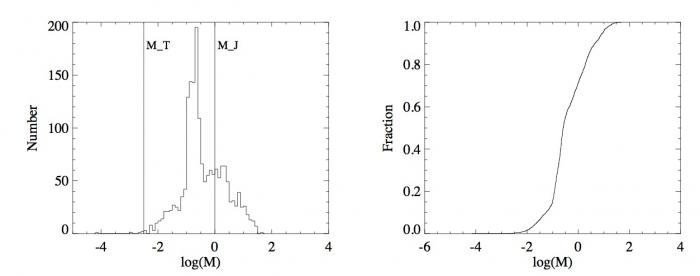
Histogrammes (gauche) et fonctions de distribution (droite) des masses des planètes du système solaire (haut) et des exoplanètes (bas). L'échelle des masses est en échelle logarithmique par soucis de clarté.
Crédit :
Sylvain Fouquet
Pour pallier le problème de la taille des intervalles pour les histogrammes, les statisticiens ont défini la fonction de distribution. Au lieu de calculer le nombre d'occurences dans un intervalle, la fonction de distribution donne le nombre d'occurences inférieures à une valeur. Par souci de comparaison, la fonction de distribution est normalisée, elle est divisée par le nombre total d'éléments de l'échantillon : 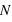 . Elle ne peut donc dépasser 1. Dans notre cas, ce
nombre est le nombre total d'exoplanètes découvertes : 1032. Le grand avantage comparé à l'histogramme est qu'il n'existe qu'une fonction de distribution pour un échantillon, alors qu'il existe un grand nombre d'histogrammes du fait du choix de la taille de l'intervalle. La fonction de distribution est clairement définie et se trouve donc être très appréciée en théorie des probabilités. La fonction de distribution des masses des exoplanètes fournit, entre autres choses, le nombre d'exoplanètes ayant une masse inférieure à 1
. Elle ne peut donc dépasser 1. Dans notre cas, ce
nombre est le nombre total d'exoplanètes découvertes : 1032. Le grand avantage comparé à l'histogramme est qu'il n'existe qu'une fonction de distribution pour un échantillon, alors qu'il existe un grand nombre d'histogrammes du fait du choix de la taille de l'intervalle. La fonction de distribution est clairement définie et se trouve donc être très appréciée en théorie des probabilités. La fonction de distribution des masses des exoplanètes fournit, entre autres choses, le nombre d'exoplanètes ayant une masse inférieure à 1 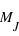 ,
, 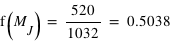 , ou à une masse terrestre,
, ou à une masse terrestre, 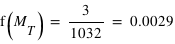 . La figure en bas à droite montre cette fonction.
. La figure en bas à droite montre cette fonction.
En dessous de la valeur minimale d'un échantillon, cette fonction est nulle. Au delà de la valeur maximale, elle vaut 1. Cette fonction est à créneaux. En passant d'une valeur de l'échantillon à une valeur plus grande elle augmente de la valeur 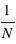 du fait de la normalisation. Entre les deux valeurs, elle est constante. Cette fonction est par construction croissante. Les "créneaux" se distinguent bien pour des échantillons avec un faible nombre d'éléments comme avec les masses des planètes du système solaire mais presque plus lorsque ce nombre est grand pour les exoplanètes (voir figures de droite).
du fait de la normalisation. Entre les deux valeurs, elle est constante. Cette fonction est par construction croissante. Les "créneaux" se distinguent bien pour des échantillons avec un faible nombre d'éléments comme avec les masses des planètes du système solaire mais presque plus lorsque ce nombre est grand pour les exoplanètes (voir figures de droite).
Comme à chaque échantillon correspond une unique fonction de distribution, il est pertinent de comparer deux fonctions de distribution. Cette comparaison indique si deux échantillons ont des propriétés similaires ou différentes. Dans le cas des planètes du système solaire comparé aux exoplanètes, il y a beaucoup de différences. Les masses des planètes du système solaire commencent à 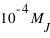 alors que celles des exoplanètes à
alors que celles des exoplanètes à 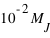 , bien qu'il y ait quelques traces d'exoplanètes en deçà de cette valeur. La pente globale de la fonction de distribution du système solaire semble régulière alors que celle des exoplanètes connaît une augmentation autour de la valeur 0,17
, bien qu'il y ait quelques traces d'exoplanètes en deçà de cette valeur. La pente globale de la fonction de distribution du système solaire semble régulière alors que celle des exoplanètes connaît une augmentation autour de la valeur 0,17 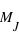 .
.
Statistique multidimensionnelle
Masse, Rayon, demi-grand axe
Gauche : Masse des exoplanètes en fonction du rayon (points) avec le cas particulier des planètes du système solaire (étoiles). Droite : demi-grand axe des exoplanètes en fonction de leur masse toujours avec le cas des planètes du système solaire (étoiles).
Crédit :
Sylvain Fouquet
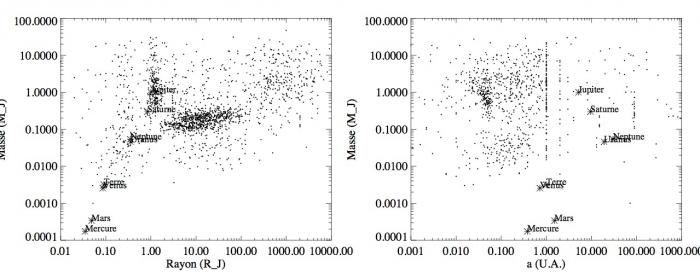
Dans ce cours, la masse des exoplanètes a été étudiée de manière indépendante des autres grandeurs des exoplanètes. Cependant, elle peut être étudiée en parallèle d'autres propriétés. Dans ce type d'étude, des corrélations entre grandeurs sont recherchées. Par exemple, si la densité des exoplanètes, 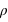 , était constante, ce qui est faux dans notre système solaire, alors le rayon,
, était constante, ce qui est faux dans notre système solaire, alors le rayon, 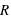 , d'une exoplanète devrait être directement corrélé avec sa masse totale,
, d'une exoplanète devrait être directement corrélé avec sa masse totale, 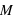 , par la loi
, par la loi 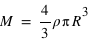 . Un graphique ayant comme abscisse le rayon au cube et comme ordonnée la masse montrerait une droite qui permettrait de calculer
. Un graphique ayant comme abscisse le rayon au cube et comme ordonnée la masse montrerait une droite qui permettrait de calculer 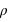 , son coefficient directeur. Dans les faits, la densité des exoplanètes n'est pas constante.
, son coefficient directeur. Dans les faits, la densité des exoplanètes n'est pas constante.
En effet, la figure de gauche montre le graphique de la masse des exoplanètes en fonction de leur rayon avec en plus le cas des huit planètes du système solaire. Deux régions plus peuplées ressortent du graphique. La première comporte des planètes de la masse de Jupiter. Dans l'autre région, les exoplanètes ont une masse d'un ordre de grandeur plus petit que Jupiter mais un rayon de 3 à 40 fois supérieur à celui de Jupiter. Les planètes de type Terre, Vénus, Mars ou Mercure sont beaucoup plus rares. Cela est seulement dû aux biais observationnels déjà mentionnés. Ce graphique montre que notre système solaire bien qu'ayant huit planètes ne contient aucune planète du type planète supergéante avec des rayons en moyenne de près de 20 fois le rayon de Jupiter. Il faut aussi se méfier de ces mesures. De telles planètes auraient, et même dépasseraient, la taille du soleil.
La figure de droite illustre le lien entre la distance exoplanète-étoile et la masse des exoplanètes. Là encore, le groupe des masses de Jupiters se distingue. Elles sont très largement aux alentours de 0,05 U.A., bien plus proche que Mercure du Soleil. Ces planètes sont donc des planètes massives collées à leurs étoiles hôtes. Elles sont alors nommées des Jupiter chauds. Encore une fois leur grand nombre apparent est très certainement dû aux observations qui détectent plus facilement ce type de planètes du fait de leurs masses et de la proximité à leurs étoiles hôtes. La grande majorité des autres exoplanètes se situent en dessous d'une U.A. Des ensembles d'exoplanètes forment des traits dans le graphique, par exemple pour la distance de 1 U.A. Cela ne signifie pas qu'il y a de nombreuses planètes se situant à 1 U.A. faisant de cette valeur une valeur exceptionnelle. Cela est sûrement dû à l'algorithme servant à mesurer le demi-grand axe qui favorise cette valeur. Il faut donc se méfier de ces valeurs. Dans ce graphique, davantage que dans le précédent, les planètes du système solaire ne semblent pas en concordance avec celles des exoplanètes. Même Jupiter qui était un cas favorable, se trouve ici avoir des propriétés bien différentes que ses homologues extra-solaires.
Statistique sur les étoiles hôtes I
Relation masse-taille des étoiles hôtes
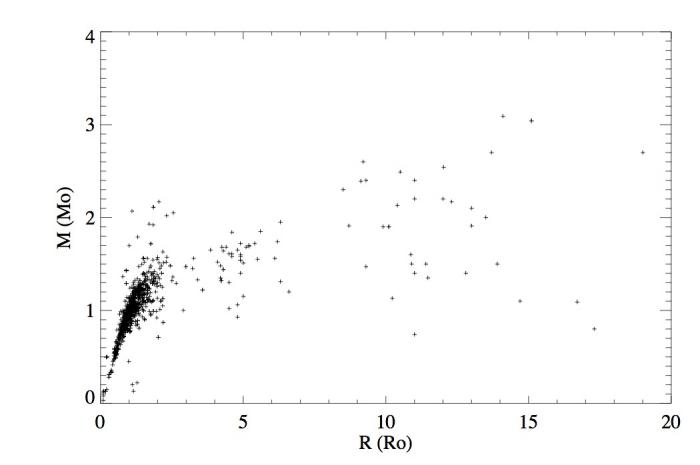
Relation masse-rayon pour les étoiles hôtes des exoplanètes. La distribution montre que les étoiles hôtes ont des propriétés similaires à celles du soleil avec des masses comprises entre 0,5 et 1,5 masse solaire et des rayons compris entre 1 et 2 rayon solaire.
Crédit :
Sylvain Fouquet
Depuis le début de ce cours, seules les propriétés des exoplanètes ont été etudiées. Cependant beaucoup d'informations peuvent être aussi obtenues sur l'étoile hôte autour de laquelle l'exoplanète gravite. En voici les principales : type spectral, masse, rayon, position dans la galaxie ou encore métallicité.
Propriétés des étoiles
Une des premières études statistiques à entreprendre est la caractérisation des étoiles hôtes par leurs masses et leurs tailles. La figure ci-contre montre la relation masse-rayon des étoiles hôtes indiquant que la grande majorité des étoiles ont des masses et des tailles proches de celle du soleil (1 Mo, 1Ro) se situant au centre de la distribution. Cependant, il ne faudrait pas conclure trop hâtivement que seules les étoiles similaires au soleil pourraient abriter des exoplanètes. Notre étoile, le soleil, est une étoile typique parmi les étoiles du disque de la Voie Lactée ; donc lorsque les astrophysiciens cherchent des exoplanètes, ils les cherchent en majorité autour d'étoiles de type solaire. Il y a donc une surreprésentation de ce type stellaire dans l'échantillon des étoiles hôtes. Pour savoir si les exoplanètes peuvent se développer autour d'étoiles ayant des propriétés très différentes de celle du soleil, il faudrait observer un grand nombres d'étoiles de types différents.
L'échantillon actuel des étoiles hôtes ne permet pas une étude poussée pour connaître l'influence de l'environnement d'une étoile hôte sur son nombre d'exoplanètes. Les étoiles proches du soleil, se situant toutes dans le disque plutôt externe de la Voie Lactée, se trouvent dans un milieu peu dense par rapport à des étoiles au centre de la Voie Lactée dans le bulbe. Une étude sur la recherche d'exoplanètes faite dans l'amas globulaire 47 Toucan peut fournir une première indication. La densité de cet amas est bien plus grande que pour les étoiles autour du Soleil. 47 Toucan a de plus des étoiles de faible métallicité, une absence de gaz et des étoiles formées il y près de 12 milliard d'années. Le résultat de cette recherche est de n'avoir trouvé aucune exoplanète alors qu'une même étude faite au voisinage du soleil aurait permis d'en découvrir une vingtaine.
Ce résultat est cohérent avec ce que l'on attend de la formation des planètes. En effet, une étoile pauvre en métaux implique que son environnement est lui-même très probablement pauvre en éléments lourds donc en matériaux pour former une planète. Les amas globulaires sont connus pour être dépourvus de gaz ce qui entraîne l'impossibilité de la formation de planètes gazeuses. De plus un environnement dense n'est pas propice à la formation et à la stabilisation dans le temps d'un disque protoplanétaire autour d'une étoile. Ce disque pourrait avoir tendance à se disperser par interaction gravitationnelle . A l'opposé, il peut être aussi instructif de rechercher des planètes dans des milieux très peu denses comme dans le halo de la Voie Lactée ou dans les galaxies naines proches de la Voie Lactée afin d'être complet.
Statistique sur les étoiles hôtes II
Relation rayon stellaire vs demi-grand axe
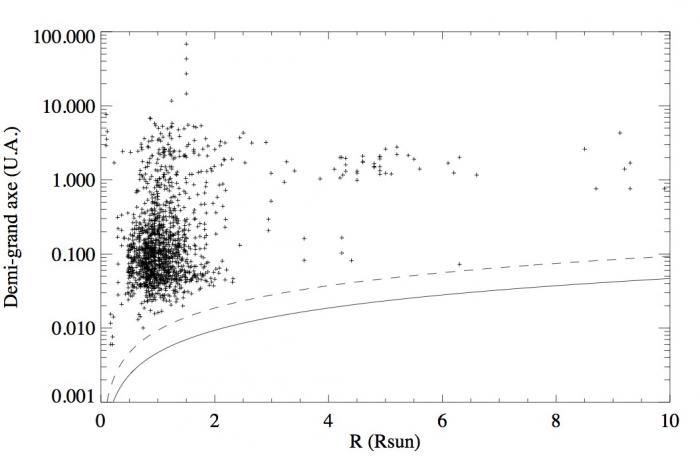
Relation entre le rayon de l'étoile hôte et le demi-grand axe de son exoplanète. La ligne en trait plein montre la limite inférieure pour les demi-grands axes dus à la taille de l'étoile convertie en U.A. La ligne en pointillé montre le double des rayons stellaires.
Crédit :
Sylvain Fouquet
Nombre d'éxoplanètes par étoile
Il est pertinent de savoir si le nombre d'exoplanètes dépend de la masse, de la taille ou du type spectral de l'étoile hôte afin, par exemple, de rechercher des exoplanètes autour d'étoiles qui ont davantage de probabilité d'en abriter. La question "Quelle est la probabilité d'avoir une exoplanète autour d'une étoile" devient alors "Quelle est la probabilité d'avoir une exoplanète autour d'une étoile de type solaire, de type géante rouge de type naine blanche, etc". Cette question permet de se familiariser avec le concept de statistiques conditionnelles ou bayésiennes qui sera développé dans la partie du cours dédié à la théorie des probabilités. La question n'est plus seulement de connaître la probabilité d'avoir un résultat mais sa probabilité à condition qu'un autre évènement ait eu lieu.
Demi-grand axe de l'exoplanète en fontion du rayon de l'étoile
Pour illustrer le concept de statistiques bayésiennes, nous exploitons la figure ci-contre présentant le demi-grand axe des exoplanètes en fonction du rayon de leurs étoiles hôtes. Premièrement, il semble qu'une planète doit être assez éloignée de son étoile hôte durant son orbite sous peine de collision et de destruction. Cela interdit donc des demi-grands axes qui sont d'une taille inférieure à celle du rayon de l'étoile hôte. De plus si une planète a une excentricité forte proche de 1 alors un demi-grand axe élevé n'empêche pas une collision lorsque l'exoplanète passe au péricentre. Dans la figure ci-contre, la ligne en trait plein et celle en tirets montrent le demi-grand axe limite dû à la taille de l'étoile et à son double. Toutes les exoplanètes ont un demi-grand axe en dehors de ces limites ; toutefois, elles sont assez proches de leurs étoiles hôtes. En effet, un demi-grand axe d'une taille de seulement dix fois le rayon de l'étoile hôte est une propriété commune. Au contraire, dans notre système solaire, Mercure est déjà à une distance de plus de 80 fois le rayon du soleil. Cette première discussion implique que plus une étoile a un grand rayon plus la probabilité de trouver une exoplanète de faible demi-grand axe sera faible. En d'autres termes, pour le même demi-grand axe une petite étoile aura plus de chance d'avoir une exoplanète qu'une étoile géante. Cela montre que la probabilité de la valeur du demi-grand axe n'est pas indépendante de la taille de l'étoile hôte, elle est conditionnée.
A l'inverse, pour les étoiles de rayon plus grand que 5 rayons solaires, le demi-grand axe des étoiles semble être statistiquement constant : aux alentours de 2 U.A. Il est évident que ce résultat est faussé par le fait que l'échantillon des étoiles géantes est petit et qu'en plus les étoiles éloignées de plusieurs U.A. sont difficiles à détecter. Cependant, supposons pour la pédagogie, ce résultat vrai. Cela implique que quelque soit la taille d'une étoile hôte entre 5 et 10 rayons solaires, son exoplanète a un demi-grand axe de près de 2 U.A. Dans ce cas, la condition sur la taille de l'étoile hôte n'a aucune influence sur la probabilité du demi-grand axe de l'exoplanète. En statistique, on dira que le demi-grand axe d'une exoplanète est indépendant du rayon de son étoile hôte lorsque ce dernier est entre 5 et 10 rayons solaires.
Signal sur Bruit
En astronomie, lorsqu'une image ou un spectre d'un objet du ciel est obtenu, le résultat varie d'une acquisition à l'autres même si la méthode utilisée est identique: même instrument, même temps de pose, etc. Cela est dû au fait que les photons collectés dans les pixels n'arrivent pas tous de manière uniforme. Si les photons d'une étoile arrivaient à une allure constante de 1 photon par milliseconde sur un pixel, alors un temps de pose de 1 seconde fournirait toujours 1000 photons. Cependant, les photons n'arrivent pas de manière ordonnée, ils suivent une loi dite de Poisson (décrite en détails dans la seconde partie du cours). Cela est dû au fait que les atomes des étoiles créant ces photons agissent de manière chaotique. Par conséquent, si on compte le nombre de photons collectés durant un temps d'une seconde sur 1000 images, on se retrouve avec un échantillon de 1000 valeurs. Il est possible de calculer la moyenne de cet échantillon que l'on note 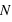 , qui est le signal recherché. L'écart-type, qui est une estimation de son erreur absolue, vaudra alors
, qui est le signal recherché. L'écart-type, qui est une estimation de son erreur absolue, vaudra alors 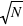 ; ceci est une propriété de la loi de Poisson. Par exemple, si N vaut 10, son erreur absolue vaut
; ceci est une propriété de la loi de Poisson. Par exemple, si N vaut 10, son erreur absolue vaut 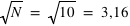 . Le rapport entre le signal, 10, et l'erreur appelé bruit, 3,16, vaut alors
. Le rapport entre le signal, 10, et l'erreur appelé bruit, 3,16, vaut alors
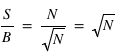
donc 3,16 dans ce cas particulier. Ce rapport s'appelle le rapport Signal sur Bruit, S/B. Dans le cas où le signal N vaut 100 alors le bruit vaut 10 et le signal sur bruit 10. On voit par cet exemple que plus le S/B est grand moins la mesure est entâchée d'erreurs, et vice versa. En astronomie, pour qu'une mesure ait un sens, un S/B d'au moins trois est requis.
Courbe transit
Courbe de transit
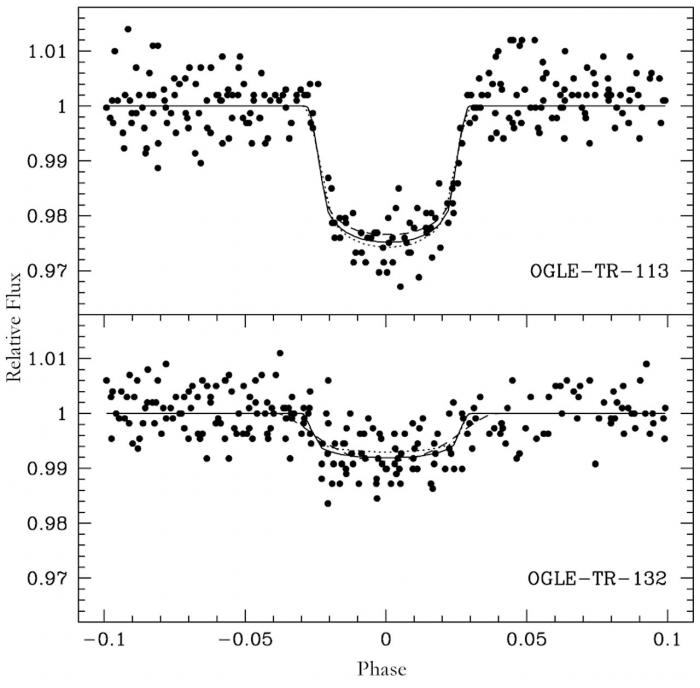
Deux courbes de transit normalisées montrant le passage d'une exoplanète devant son étoile hôte.
Crédit :
ESO
La figure ci-contre illustre, dans le cas plus particulier de la détection des exoplanètes par transit, l'influence du bruit pour détecter une exoplanète. Le graphique supérieur montre un transit assez évident avec une chute puis une remontée de la luminosité . La courbe noire est l'ajustement théorique du flux. Cela représente la courbe sans le bruit, sans la dispersion statistique. Plus réalistes, les points montrent les observations qui sont composées du signal et du bruit. Les courbes sont ici normalisées à 1. Pour le graphique du bas, la décroissance est visible mais plus difficile à modéliser correctement car elle est moins forte. Les deux courbes montrent la présence d'une planète avec des rapports S/B proche de 20. En effet pour un signal de 1 le bruit est de l'ordre de 0,05. Cependant si ce S/B est suffisant pour détecter les deux exoplanètes, il donnera une meilleure précision sur les propriétés (masse, rayon, ...) de l'exoplanète du graphique du haut car le profil de luminosité est plus profond que pour l'exoplanète du graphique du bas.
Probabilités
Auteur: Sylvain Fouquet
Probabilités
Statistique et probabilité sont deux côtés d'une même pièce. Ces deux domaines des mathématiques s'occupent de décrire le résultat d'expériences ou d'observations faisant intervenir le hasard. Par exemple, tirer un bulletin dans une urne, choisir des personnes au hasard dans un groupe, sélectionner des étoiles au hasard dans le ciel, etc, ne peuvent pas se décrire par la mécanique classique, l'hydrodynamique ou encore le magnétisme mais par la statistique et les probabilités. Pourquoi avoir deux noms ? Statistique et probabilité ne sont pas identiques dans la démarche bien que traitant des mêmes sujets. La statistique sert à observer et décrire le monde alors que les probabilités, aussi appelés théorie de la probabilité, tentent de l'expliquer théoriquement, mathématiquement. Ces deux approches se complètent mutuellement comme l'observation physique et le modèle mathématique se complètent.
L'expérience de 100 lancers du même dé servira à illustrer la différence entre statistique et probabilité. Lors de cette expérience, la statistique décrit les propriétés statistiques de ces 100 lancers. Par exemple, la statistique montre que chaque face du dé est presque apparue autant de fois. La valeur moyenne se rapproche de 3,5. De manière complémentaire à cet aspect observationnel, la théorie de la probabilité prouve que si vous avez un dé non pipé, il y a autant de chance de tomber sur une face que sur une autre. Pour un nombre de 100 lancers, la théorie de la probabilité indique quelle est la chance d'obtenir la face 1 par exemple. Les prévisions de la théorie de la probabilité doivent se confirmer dans les résultats observationels de la statistique. Si tel n'est pas le cas pour les lancers de dé, cela veut dire que le dé est pipé et qu'il faut changer les lois de probabilité (passer de la loi "chaque valeur a une chance sur 6 de sortir" à une loi plus compliquée qui va définir le dé pipé), à l'instar d'une expérience mettant en échec une théorie physique.
Les variables aléatoires
L'univers des événements
En probabilité, les variables sont dites aléatoires car pour, une même expérience, la mesure de la même observable sera différente, aléatoire. Par exemple lorsqu'un dé est lancé, l'observable qui est le numéro du dé est aléatoire (à moins qu'il ne soit envoyé par une machine pouvant envoyer le dé à chaque fois exactement de la même façon). Ce qui importe pour une variable aléatoire c'est l'ensemble des valeurs qu'elle peut prendre. Pour un dé, il y a six faces ; le nombre d'événements possibles est six (on suppose que le dé ne peut pas s'arrêter sur une arête). Autre exemple, la variable donnant l'instant du prochain accident de voiture en France peut prendre n'importe quelle valeur à priori entre 0 seconde et l'infini : 1 secondes, 10 minutes, 1 heures, etc. Il y a une infinité de possibilités.
Il existe donc deux types de variables aléatoires : les variables discrètes (lancer de dés) et les variables continues (temps entre deux accidents). Pour les variables discrètes, le nombre d'evénements peut être fini ou infini. Il est toujours infini pour une variable continue. L'ensemble des évènements est appelé l'ensemble univers des évènements. La suite donne quelques exemples détaillés de ces types d'ensembles. En probabilité, les événements sont très souvent associés à des nombres pour pouvoir être traités mathématiquement. Par exemple pour un jeu de cartes, la carte roi de pique peut être associée à la valeur numérique de 25.
Exemples de variables discrètes
L'ensemble univers le plus connu et le plus simple de tous est l'ensemble des évènements d'un jet d'une pièce de monnaie. Il n'y a que deux évènements : {pile ; face} (trois évènements si l'on prend en compte le cas où la pièce reste sur son bord). Par commodité, on utilise l'ensemble {0, 1} en liant pile à 0 et face à 1.
L'autre variable aléatoire très connue est le lancer de dé avec ses six évènements possibles qui sont déjà des nombres : {1, 2, 3, 4, 5, 6}. Il est aussi possible de lancer deux dés à la fois et de sommer leurs résultats. Dans ce cas, cela conduit à un ensemble de 11 évènements {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}.
Des urnes remplies de boules de différentes couleurs sont aussi un exemple très pédagogiques d'ensemble univers. Par exemple, pour une urne remplie de 5 boules qui ne se différencient que par leurs couleurs : 2 noires, 2 blanches et 1 rouge, l'ensemble des évènements si l'on tire une boule est {noire, blanche, rouge}. Si l'on en tire deux, c'est alors {(noire, noire), (noire, blanche), (noire, rouge), (blanche, rouge)}. Encore une fois, il faut associer chaque couleur à un nombre pour pouvoir travailler dessus.
Enfin, pour les joueurs d'argent, et les aficionados de probabilités à variables discrètes, le casino est l'endroit rêvé. Il est possible de trouver là une multitude de jeux avec des ensembles univers allant de la case rouge ou noir à des images sur une machine à sous. Les casinos utilisent bien évidemment aussi les jeux de cartes pour enrichir le nombre d'évènement possibles.
Bref, les variables aléatoires discrètes sont partout dans la société. C'est d'ailleurs souvent à la suite de créations de la société : pièces, dés, cartes, roulette, loto, ...
Exemples de variables continues
Les variables continues se trouvent plus souvent liées à des propriétés physiques de la nature. Un exemple simple peut se trouver dans les prévisions météorologiques : "Quand pleuvra-t-il chez moi ?". La réponse se trouve être entre tout de suite (0 seconde) et jamais (un temps infini). Il y a donc une infinité continue de durées possibles. Il peut se passer plusieurs jours sans pleuvoir alors que parfois moins d'une heure s'écoule entre deux averses. Cet exemple de variable aléatoire est similaire à celui de l'intervalle de temps entre deux accidents de voitures. Plus généralement, il se trouve que certains phénomènes naturels n'arrivent pas de manière régulière. On peut alors introduire la variable aléatoire qui donne le temps entre deux occurences.
Un autre type de variables aléatoires continues sont les incertitudes dues à de faibles changements des conditions initiales. Refaire exactement la même chose un grand nombre de fois donne un résultat similaire mais pas identique. Lancer un poids est un de ces cas. Vous aurez beau faire attention, vous ne lancerez jamais avec exactement la même force, dans la même position et dans les mêmes conditions (vent, atterissage, etc). La conséquence est que le poids ne tombera jamais au même endroit. Il en est de même pour la production de pièces en série qui ne sont jamais tout à fait identiques. Tous ces cas peuvent se traiter avec les variables aléatoires continues.
La fonction de probabilité
En probabilité, après avoir défini l'ensemble univers des évènements, il reste à associer à chaque évènement sa probabilité de se produire via la fonction de probabilité. Cette fonction prend des valeurs entre 0 et 1. La valeur 0 signifie que l'évènement est impossible, la valeur 1 qu'il est certain.
Par exemple, dans le cas d'un jet d'une pièce non faussée, l'ensemble des évènements est {pile, face}, ou {0, 1}, et la fonction de probabilité, notée 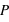 , donne
, donne 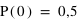 et
et 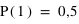 . Cela signifie qu'il y a la même chance de tomber sur pile que sur face. Par contre si la pièce était faussée, il serait possible d'avoir une fonction de probabilité donnant :
. Cela signifie qu'il y a la même chance de tomber sur pile que sur face. Par contre si la pièce était faussée, il serait possible d'avoir une fonction de probabilité donnant : 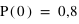 et
et 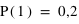 . "pile" aurait alors 4 fois plus de chance de sortir.
. "pile" aurait alors 4 fois plus de chance de sortir.
Cette loi nous amène à une propriété bien naturelle des probabilités.
La probabilité de l'ensemble univers vaut 1 : P(Univers) = 1.
En effet, il est certain que la variable aléatoire sorte un évènement de l'ensemble univers. Dans le cas d'un lancer de dé, P({1, 2, 3, 4, 5, 6}) = 1, car on est sûr d'obtenir comme résultat 1, 2, 3, 4, 5 ou 6. A l'inverse, l'ensemble vide {} a toujours une probabilité nulle : P({}) = 0.
Probabilité sur des sous-ensembles d'événements
Dans le cas, d'un dé non pipé, la fonction de probabilité est pour tous 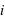 de 1 à 6,
de 1 à 6, 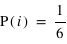 . Il y a en effet autant de chance de tirer un 1, un 2, etc. Cependant quelle est la probabilité de tirer un nombre pair, {2, 4, 6} ? Intuitivement, cette probabilité doit être plus grande que de tirer seulement un 2. Le bon sens et la construction de la théorie des probabilités impliquent qu'elle corresponde à la somme de chacune de leur probabilité. Donc
. Il y a en effet autant de chance de tirer un 1, un 2, etc. Cependant quelle est la probabilité de tirer un nombre pair, {2, 4, 6} ? Intuitivement, cette probabilité doit être plus grande que de tirer seulement un 2. Le bon sens et la construction de la théorie des probabilités impliquent qu'elle corresponde à la somme de chacune de leur probabilité. Donc 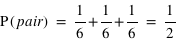 . Il en est de même pour la probabilité de tirer un nombre impair. Ce petit exemple illustre une loi simple de probabilité. La détermination de la probabilité d'un sous-ensemble est égale à la somme de la probabilité de chacun des événements du sous-ensemble.
. Il en est de même pour la probabilité de tirer un nombre impair. Ce petit exemple illustre une loi simple de probabilité. La détermination de la probabilité d'un sous-ensemble est égale à la somme de la probabilité de chacun des événements du sous-ensemble.
Voyons comment calculer la probabilité de l'union de deux sous-ensembles. Par exemple au jeu de 52 cartes, la probabilité de tirer n'importe quelle carte est la même et vaut 1/52. Dans ce cas, la probabilité de tirer une carte rouge vaudra 1/52  26 = 1/2 car il y a 26 cartes rouges, la moitié du nombre des cartes. La probabilité de tirer une carte noire vaut aussi 1/2, quant à celle de tirer un coeur, elle vaut 1/4 et celle de tirer un roi 1/13. Quelle est alors la probabilité de tirer une carte rouge ou noire ? ou la probabilité de tirer une carte rouge ou de coeur ? ou encore une carte rouge ou un roi ? Pour la première probabilité, intuitivement le résultat est 1 car c'est l'ensemble univers. Cela revient à la somme des probabilités des sous-ensembles : 1/2+1/2. Pour la seconde, la probabilité reste celle de tirer une carte rouge, 1/2, car obligatoirement un coeur est une carte rouge. On n'additionne donc pas les probabilités. Le dernier cas est plus compliqué car deux rois font partie de l'ensemble des cartes rouges mais les deux autres non. Comment faire ? La relation donnant la solution générale est
26 = 1/2 car il y a 26 cartes rouges, la moitié du nombre des cartes. La probabilité de tirer une carte noire vaut aussi 1/2, quant à celle de tirer un coeur, elle vaut 1/4 et celle de tirer un roi 1/13. Quelle est alors la probabilité de tirer une carte rouge ou noire ? ou la probabilité de tirer une carte rouge ou de coeur ? ou encore une carte rouge ou un roi ? Pour la première probabilité, intuitivement le résultat est 1 car c'est l'ensemble univers. Cela revient à la somme des probabilités des sous-ensembles : 1/2+1/2. Pour la seconde, la probabilité reste celle de tirer une carte rouge, 1/2, car obligatoirement un coeur est une carte rouge. On n'additionne donc pas les probabilités. Le dernier cas est plus compliqué car deux rois font partie de l'ensemble des cartes rouges mais les deux autres non. Comment faire ? La relation donnant la solution générale est
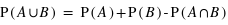
où A et B sont deux sous-ensembles de l'ensemble univers, 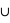 l'union de deux ensembles et
l'union de deux ensembles et 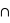 leur intersection. Vous pouvez vérifier que cela donne bien les résultats des deux premiers exemples. Dans le cas des rois, la probabilité est alors P(rouge
leur intersection. Vous pouvez vérifier que cela donne bien les résultats des deux premiers exemples. Dans le cas des rois, la probabilité est alors P(rouge 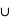 rois) = P(rouge) + P(rois) - P(rois
rois) = P(rouge) + P(rois) - P(rois 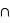 rouge). Il se trouve que l'ensemble {rois
rouge). Il se trouve que l'ensemble {rois 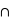 rouge} n'est formé que des deux rois rouges, donc sa probabilité est 2
rouge} n'est formé que des deux rois rouges, donc sa probabilité est 2 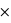 1/52 = 1/26. Le résultat est donc P(rois
1/52 = 1/26. Le résultat est donc P(rois 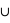 rouge) = 1/2 + 1/13 - 1/26 = 1/2 + 1/26 = 14/26.
rouge) = 1/2 + 1/13 - 1/26 = 1/2 + 1/26 = 14/26.
Notons que si {A 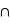 B} = {}, donc si A et B sont disjoints, il suffit alors de sommer la probabilité de A et de B pour avoir celle de A
B} = {}, donc si A et B sont disjoints, il suffit alors de sommer la probabilité de A et de B pour avoir celle de A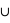 B car P({}) = 0.
B car P({}) = 0.
Calcul de la fonction de probabilité
Équipartition
Dans le cas d'un ensemble fini, il est parfois très facile de calculer la fonction de probabilité. Il suffit que tous les événements soient équiprobables, c'est à dire qu'ils aient la même probabilité, notée 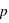 . Cela est vrai pour un jet de dé ou de pièce non faussés, ou pour un jeu de cartes bien mélangé. Dans ce cas, la probabilité de tous les évènements, donc de l'ensemble univers, vaut P({E1, E2, E3, ..., En}) = P({E1}) + P({E2})+ P({E3})+ ... + P({En}) = p +p +p +...+p =
. Cela est vrai pour un jet de dé ou de pièce non faussés, ou pour un jeu de cartes bien mélangé. Dans ce cas, la probabilité de tous les évènements, donc de l'ensemble univers, vaut P({E1, E2, E3, ..., En}) = P({E1}) + P({E2})+ P({E3})+ ... + P({En}) = p +p +p +...+p = 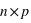 car tous les ensembles d'évènements sont disjoints, c'est à dire pour tous
car tous les ensembles d'évènements sont disjoints, c'est à dire pour tous 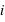 et
et 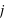 , {
, {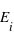
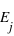 } = {}. Or la probabilité de l'ensemble univers vaut par définition 1. Donc
} = {}. Or la probabilité de l'ensemble univers vaut par définition 1. Donc 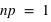 ce qui implique que
ce qui implique que 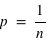 . Cela justifie pourquoi la probabilité pour le lancer d'une pièce vaut 1/2, pour le jet d'un dé vaut 1/6 et pour le tirage d'une carte dans un jeu de 52 cartes vaut 1/52.
. Cela justifie pourquoi la probabilité pour le lancer d'une pièce vaut 1/2, pour le jet d'un dé vaut 1/6 et pour le tirage d'une carte dans un jeu de 52 cartes vaut 1/52.

Loi des grands nombres
Lorsqu'il n'y a pas équipartition dans les probabilités, il est moins direct de déduire la loi de probabilité. Une façon simple en théorie mais hélas irréalisable en pratique est la loi des grands nombres. Pour connaître la loi de probabilité, il suffit de mesurer plusieurs fois la valeur d'une variable aléatoire, de compter combien de fois sortent les mêmes valeurs puis de diviser ces nombres par le nombre total d'essais. Ainsi pour connaître la loi d'un dé, il suffit de faire une grand nombre de lancers, 1000 par exemple, et de regarder combien de 1 de 2 de 3, ... et de 6 sont sortis et enfin de diviser ces nombres d'occurences par le nombre total de lancers, 1000 dans ce cas. Cela fournit une valeur proche de la probabilité de chaque évènement mais pas exacte. La théorie mathématique prouve que si le nombre total d'essais est infini (ce qui est évidemment impossible en pratique), on en déduit alors la probabilité exacte pour chaque événement.

Pour des variables continues où les résultats sont des réels, deux résultats ne peuvent jamais être identiques car la chance d'avoir exactement deux réels identiques est nulle. Ce qui est mesuré est la probabilité d'avoir des valeurs dans un petit intervalle autour d'une valeur donnée. De toute façon, les outils de mesure n'étant pas parfaits, il est impossible de mesurer avec une précision infinie. La largeur des intervalles considérés dépendra donc de la précision des mesures.
Introduction aux théorème de Bayes - Découvrir la bonne urne
Considérons deux urnes, l'une remplie de 9 boules blanches et d'une seule boule noire, appelée A, et l'autre remplie de 9 boules noires et d'une boule blanche, appelée B. Il est interdit de voir leur contenu, on ne peut qu''en extraire une boule. Le problème est de savoir quelle est l'urne A parmi les deux urnes ? Sans faire aucun tirage de boule, la probabilité qu'une urne donnée soit l'urne A est la même pour les deux urnes et vaut donc 0,5, une chance sur deux, car il n'y a que deux événements.
Le problème ici n'est pas de connaître la probabilité de tirer des boules blanches ou noires dans les urnes A ou B mais de savoir depuis quelle urne sont tirées les boules en s'aidant du résultat du tirage d'une urne. Ce sont alors des probabilités conditionnelles : sachant qu'un résultat est vrai, quelle est la probabilité qu'un autre le soit aussi ? Ce problème simple d'urne peut s'extrapoler dans le cas de théories physiques. Imaginons que deux théories (deux urnes) soient en concurrence pour expliquer les mêmes phénomènes statistiques (tirage de boules). En faisant quelques observations (en tirant quelques boules), il est alors possible de montrer qu'une théorie est plus probable qu'une autre. Il est aussi possible que les deux théories se trompent (en tirant une boule rouge d'une des deux urnes).
De plus, avec les probabilités conditionnelles, il est possible d'estimer des grandeurs physiques via la mesure d'autres grandeurs. Un exemple caricatural éclaircira ce principe. Ayant les yeux bandés, je cherche à savoir si j'ai devant moi un norvégien ou un espagnol. Je peux estimer la taille de la personne mais pas voir son passeport. Comme j'ai une pensée très caricaturale, pour moi tous les norvégiens sont grands blonds aux yeux bleux et tous les espagnols sont petits bruns aux yeux marrons. Donc si j'ai devant moi une personne plutôt grande, je dirai que c'est un norvégien. De plus, s'il m'est permis de ne regarder que ses cheveux et qu'ils sont blonds, ma certitude grandit. La taille et la couleur des cheveux que j'ai pu observer servent à estimer avec une certaine probabilité la nationalité d'une personne. Cette méthode repose sur une loi conditionnelle implicite qui est qu'un homme grand aux yeux bleus à une plus forte probabilité d'être norvégien qu'espagnol. Cette démarche est beaucoup utilisée en astrophysique pour déterminer des propriétés inaccessibles par des mesures directes, mais déductibles par d'autres propriétés observables. Cependant, il est important de se souvenir que ce ne sont que des probabilités. D'autre part, cela suppose que les lois conditionnelles supposées a priori soient correctes.
Théorème de Bayes
Venons-en aux formules qui permettent concrètement de résoudre le problème de l'urne. Soient A et B deux expériences. La probabilité de A sachant B vrai, noté P(A|B), est donnée par la loi suivante, dite formule de Bayes établie par le mathématicien et pasteur Thomas Bayes au XVIIIe siècle :
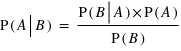
Il suffit de connaître P(A), P(B) et P(B|A) pour en déduire P(A|B).
Ce théorème provient du fait que 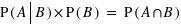 et que, de même,
et que, de même, 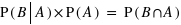 donc que
donc que 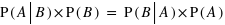 .
.
Dans le cas particulier des urnes, si l'on tire une boule blanche quelle est alors la probabilité que ce soit de l'urne A, probabilité notée P(Urne A|Blanche), ou de l'urne B, P(Urne B|Blanche) ? Dans le cas de l'urne A, il faut calculer les trois probabilités P(Blanche|Urne A), P(Urne A) et P(Blanche). La probabilité de tirer une boule blanche dans l'urne A est P(Blanche|Urne A) = 9/10. La probabilité de choisir l'urne A ou B est identique au début de l'expérience et vaut P(Urne A) = P(Urne B) = 0,5. Enfin la probabilité de tirer une boule blanche est P(Urne A)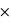 P(Blanche|Urne A)+P(Urne B)
P(Blanche|Urne A)+P(Urne B)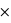 P(Blanche|Urne B) = 0,5
P(Blanche|Urne B) = 0,5 9/10 + 0,5
9/10 + 0,5 1/10 = 0,5 car il est possible de tirer une boule blanche depuis l'urne A ou depuis l'urne B, mais pas avec la même probabilité. Ainsi, la probabilité que l'on soit en présence de l'urne A sachant que l'on a tiré une boule blanche est donnée par P(Urne A|Blanche) = P(Blanche|Urne A)
1/10 = 0,5 car il est possible de tirer une boule blanche depuis l'urne A ou depuis l'urne B, mais pas avec la même probabilité. Ainsi, la probabilité que l'on soit en présence de l'urne A sachant que l'on a tiré une boule blanche est donnée par P(Urne A|Blanche) = P(Blanche|Urne A) P(Urne A)/P(Blanche) = 9/10
P(Urne A)/P(Blanche) = 9/10 0,5/0,5 = 9/10. Dans l'autre cas P(Blanche|Urne B) = 1/10. Avec cette observation du tirage d'une boule blanche, on est passé d'une probabilité de 0,5 pour que l'urne étudiée soit l'urne A, à une probabilité de 9/10 pour que l'urne étudiée soit l'urne A.
0,5/0,5 = 9/10. Dans l'autre cas P(Blanche|Urne B) = 1/10. Avec cette observation du tirage d'une boule blanche, on est passé d'une probabilité de 0,5 pour que l'urne étudiée soit l'urne A, à une probabilité de 9/10 pour que l'urne étudiée soit l'urne A.
Grandeurs classiques en probabilité
L'espérance
En théorie des probabilités, l'espérance est la valeur moyenne à laquelle on s'attend pour une variable aléatoire suivant une loi de probabilité donnée. Elle se définit dans le cas d'une variable discrète par la relation suivante : 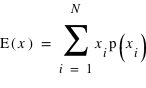 . De manière similaire, elle se définit pour une variable continue
. De manière similaire, elle se définit pour une variable continue 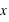 :
: 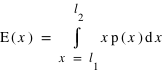 où
où 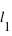 et
et 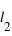 sont les limites inférieures et supérieures que peut prendre la variable
sont les limites inférieures et supérieures que peut prendre la variable 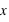 .
.
Un exemple dans la cas d'une variable discrète est la moyenne au lancer d'un dé. L'espérance est alors 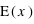 = 1×1/6+2×1/6+3×1/6+4×1/6+5×1/6+6×1/6 = 21/6 = 3,5. Dans le cas d'une variable continue comme la loi uniforme de 0 à 1 (
= 1×1/6+2×1/6+3×1/6+4×1/6+5×1/6+6×1/6 = 21/6 = 3,5. Dans le cas d'une variable continue comme la loi uniforme de 0 à 1 (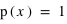 ), l'espérance est
), l'espérance est 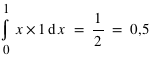 . Moyenne et espérance se ressemblent beaucoup, cependant elle ont une différence. L'espérance est une valeur dans le cadre de la théorie des probabilités associée à une loi de probabilité. La moyenne est, quant à elle, le résultat d'une opération arithmétique sur un échantillon. La moyenne dépend donc de l'échantillon alors que l'espérance est théorique et donc unique pour une loi donnée. La moyenne calculée à partir d'un échantillon doit être proche de l'espérance mais pas forcément identique. Par exemple, lorsqu'un dé est tiré 10 fois et que la moyenne des résultats est faite, le résultat n'est pas forcément l'espérance de 3,5. De plus, si l'on refait 10 lancers la nouvelle moyenne ne sera pas forcément identique à la première. Cependant, d'après la loi des grands nombres, plus le nombre de lancers de dé sera grand, plus la moyenne s'approchera de l'espérance. L'espérance doit être vue comme la limite de la moyenne lorsque l'on fait tendre le nombre d'essais vers l'infini.
. Moyenne et espérance se ressemblent beaucoup, cependant elle ont une différence. L'espérance est une valeur dans le cadre de la théorie des probabilités associée à une loi de probabilité. La moyenne est, quant à elle, le résultat d'une opération arithmétique sur un échantillon. La moyenne dépend donc de l'échantillon alors que l'espérance est théorique et donc unique pour une loi donnée. La moyenne calculée à partir d'un échantillon doit être proche de l'espérance mais pas forcément identique. Par exemple, lorsqu'un dé est tiré 10 fois et que la moyenne des résultats est faite, le résultat n'est pas forcément l'espérance de 3,5. De plus, si l'on refait 10 lancers la nouvelle moyenne ne sera pas forcément identique à la première. Cependant, d'après la loi des grands nombres, plus le nombre de lancers de dé sera grand, plus la moyenne s'approchera de l'espérance. L'espérance doit être vue comme la limite de la moyenne lorsque l'on fait tendre le nombre d'essais vers l'infini.
Le moment d'ordre deux centré - la variance
La variance ou "moment d'ordre deux centré" est une mesure du carré de la dispersion d'une variable aléatoire autour de son espérance. En d'autres termes, la variance donne une information sur la dispersion de la variable aléatoire autour de l'espérance. Plus la variance est grande plus les valeurs de la variable aléatoire auront de chance d'être loin de l'espérance, et vice versa. Une variance faible donnera une loi de probabilité piquée autour de l'espérance. Pour une variable discrète, la variance se définit comme suit : 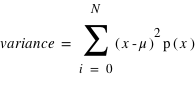 avec
avec 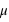 l'espérance. Dans le cas d'une variable continue,
l'espérance. Dans le cas d'une variable continue, 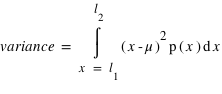 . On peut aussi définir la variance en n'utilisant que l'espérance de la variable
. On peut aussi définir la variance en n'utilisant que l'espérance de la variable 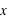 et
et 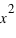 :
: 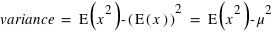 . La démonstration est demandée en exercice. L'écart-type, souvent noté
. La démonstration est demandée en exercice. L'écart-type, souvent noté 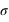 , est la racine carrée de la variance :
, est la racine carrée de la variance : 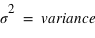 . De même que pour le couple espérance-moyenne, le terme variance s'utilise plutôt en probabilité et écart-type en statistique.
. De même que pour le couple espérance-moyenne, le terme variance s'utilise plutôt en probabilité et écart-type en statistique.
Pour le lancer de dé non biaisé, la variance vaut environ 2,91667 et donc l'écart type vaut environ 1,70783. Pour la loi uniforme de 0 à 1, la variance vaut 1/12 ≈ 0,0833.
Fonctions de distribution
Fonctions de distribution
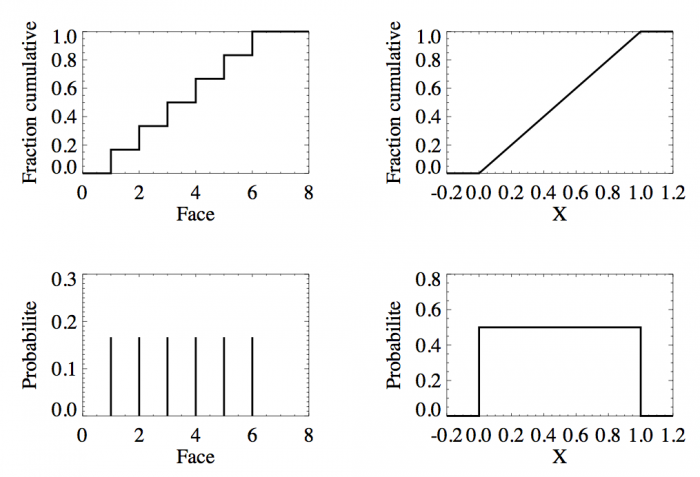
Fonctions de distribution (en haut) et lois de probabilité (en bas) du lancer d'un dé (à gauche) et de la loi uniforme sur [0, 1] (à droite).
Crédit :
Sylvain Fouquet
Avant de décrire plusieurs lois de probabilité utiles car très courantes, cette section décrit l'outil majeur qu'est la fonction de distribution et sa dérivée, la loi de probabilité.
Fonction de distribution
Pour une variable aléatoire notée 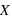 , la fonction de distribution, notée
, la fonction de distribution, notée 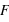 , donne la probabilité d'avoir la variable
, donne la probabilité d'avoir la variable 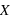 strictement plus petite que
strictement plus petite que 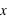 :
: 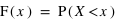 . La fonction
. La fonction  est donc par définition une fonction croissante et bornée par la valeur 1. Cette définition convient aussi bien aux variables discrètes qu'aux variables continues. Il est aisé avec cette fonction de calculer la probabilité d'avoir la variable
est donc par définition une fonction croissante et bornée par la valeur 1. Cette définition convient aussi bien aux variables discrètes qu'aux variables continues. Il est aisé avec cette fonction de calculer la probabilité d'avoir la variable 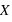 entre
entre 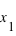 et
et 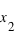 . C'est tout simplement
. C'est tout simplement 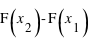 . En conséquence, si la courbe est plate ou avec une pente faible entre deux points
. En conséquence, si la courbe est plate ou avec une pente faible entre deux points 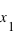 et
et 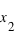 , cela conduit à une probabilité entre
, cela conduit à une probabilité entre 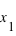 et
et 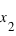 faible alors que si la pente est forte la probabilité l'est aussi.
faible alors que si la pente est forte la probabilité l'est aussi.
La figure en haut à gauche montre la fonction de distribution d'un dé. Pour 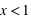 , la fonction est nulle, il est en effet impossible qu'un jet de dé puisse sortir un nombre plus petit que 1. De
, la fonction est nulle, il est en effet impossible qu'un jet de dé puisse sortir un nombre plus petit que 1. De 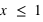 à
à 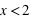 ,
,  est constante et vaut 1/6 qui est la probabilité d'avoir un 1 à un jet de dé. Ensuite entre 2 et 3 exclus, la fonction vaut
est constante et vaut 1/6 qui est la probabilité d'avoir un 1 à un jet de dé. Ensuite entre 2 et 3 exclus, la fonction vaut 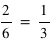 ; cela correspond à la probabilité de sortir un 1 ou un 2. La fonction continue d'augmenter pour plafonner jusqu'à x>6 où elle atteint sa valeur maximale de 1 car il est certain qu'un dé sorte un chiffre plus petit ou égale à 6.
; cela correspond à la probabilité de sortir un 1 ou un 2. La fonction continue d'augmenter pour plafonner jusqu'à x>6 où elle atteint sa valeur maximale de 1 car il est certain qu'un dé sorte un chiffre plus petit ou égale à 6.
La figure en haut à droite montre la fonction de distribution d'une variable continue. En dessous de 0, sa valeur est nulle au dessus de 1 elle vaut 1. Les valeurs possibles de cette variable sont donc comprises entre 0 et 1 inclus. La pente est une droite ; pour n'importe quel intervalle entre 0 et 1 de même taille la probabilité est donc la même. En conséquence, la probabilité d'avoir une valeur entre [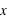 ,
, 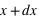 ] est identique. Cette fonction de distribution n'est autre que la fonction de distribution de la loi uniforme entre 0 et 1 ; chaque nombre entre 0 et 1 ayant la même chance d'être tiré.
] est identique. Cette fonction de distribution n'est autre que la fonction de distribution de la loi uniforme entre 0 et 1 ; chaque nombre entre 0 et 1 ayant la même chance d'être tiré.
Loi de probabilité
La fonction de distribution est l'outil statistique par excellence en probabilité. Cependant, d'un point de vue pratique, on lui préfère sa dérivée qui est plus parlante : la loi de probabilité. En effet, c'est la pente de la fonction de distribution qui indique si une valeur a une forte probabilité ou pas de survenir. Cela revient en statistique à faire l'histogramme vu aussi dans la première partie de ce cours.
La figure en bas à gauche montre la dérivée de la fonction de distribution pour un lancer de dé. On retrouve le résultat classique qui veut que la probabilité de sortir un 1, 2, 3, 4, 5, ou 6 soit identique et égale à 1/6. La figure en bas à droite fait de même mais avec la loi uniforme entre 0 et 1. La fonction est une courbe plate montrant bien que chaque valeur a une même probabilité.
Par la suite et pour finir cette partie théorique, plusieurs lois de probabilité incontournables sont passées en revue. La liste est évidemment non exhaustive.
Loi binomiale
La loi binomiale
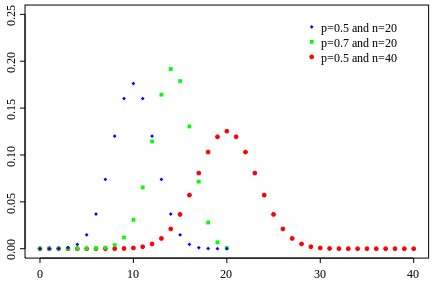
Exemples de lois binomiales pour différent nombre de répétition (
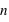
) d'une loi à deux évènements et pour différentes probabilités de l'évènement 0 (
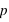
). Pour le même nombre de lancers
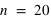
, le pic est à 14 avec un probabilté
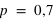
et seulement 10 avec
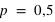
. Pour
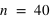
et
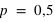
, le pic est à 20, à la moitié du nombre de lancers, car il y autant de chance d'avoir l'évènement 0 que 1. En comparaison de
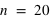
et
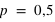
, lorsque
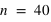
, la fonction a un pic moins haut mais plus reséré, cela est dû au fait que le rapport entre l'espérance et l'écart type tend vers 0 lorsque
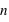
tend vers l'infini.
Crédit :
Wikipédia
Loi binomiale
En compléxifiant la loi vue ci-dessus, il est possible de créer la loi binomiale. Cette dernière s'intéresse aux résultats de plusieurs lancers d'une expérience n'ayant que deux événements possibles. Par exemple, lorsqu'une pièce est lancée 20 fois de suite, quelle est la probabilité d'avoir 10 faces ou 3 piles ou même 20 faces de suite ? La loi binomiale dépend donc de deux paramètres : la propabilité 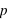 de la loi à deux événements et le nombre de répétition de cette loi,
de la loi à deux événements et le nombre de répétition de cette loi, 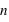 . Son ensemble univers est constitué de toutes les séries possibles de
. Son ensemble univers est constitué de toutes les séries possibles de 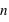 répétitions de la loi à deux évènements. Le nombre d'événements vaut donc
répétitions de la loi à deux évènements. Le nombre d'événements vaut donc 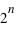 car à chaque répétition (
car à chaque répétition (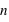 en tout) il y a deux événements possibles. Par exemple, lancer une pièce trois fois donne
en tout) il y a deux événements possibles. Par exemple, lancer une pièce trois fois donne 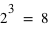 évènements possibles. L'ensemble univers est en ce cas : (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Chaque évènement est donc constitué d'un certain nombre de 0, noté
évènements possibles. L'ensemble univers est en ce cas : (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Chaque évènement est donc constitué d'un certain nombre de 0, noté 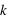 , et de 1, noté
, et de 1, noté 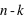 . Par définition la probabilité de 0 vaut
. Par définition la probabilité de 0 vaut 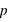 et celle de 1 vaut
et celle de 1 vaut 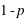 . Donc la probabilité d'un évènement est
. Donc la probabilité d'un évènement est 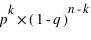 . L'intérêt dans ce type d'expérience est de savoir combien de fois sort l'évènement 0 ou 1 mais sans se soucier de l'ordre. Les évènements (0, 1, 0) ou (1, 0, 0) sont alors considérés comme identiques. La loi binomiale fournit la probabilité de tirer
. L'intérêt dans ce type d'expérience est de savoir combien de fois sort l'évènement 0 ou 1 mais sans se soucier de l'ordre. Les évènements (0, 1, 0) ou (1, 0, 0) sont alors considérés comme identiques. La loi binomiale fournit la probabilité de tirer 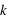 évènements 0 sur
évènements 0 sur 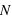 lancers. Pour cela, il suffit de remarquer que pour un nombre
lancers. Pour cela, il suffit de remarquer que pour un nombre 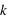 d'événements 0 parmi
d'événements 0 parmi 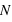 lancers, il est possible d'effectuer
lancers, il est possible d'effectuer 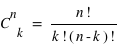 permutations. Donc la probabilité recherchée, notée
permutations. Donc la probabilité recherchée, notée 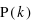 , vaut
, vaut 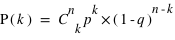 .
.
Propriétés de la loi binomiale
Sur 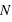 lancers, plus un évènement aura une grande probabilité plus il sortira souvent. Cependant, il est rare qu'il sorte pour chaque lancer. En conséquence, le pic de probabilité de la loi binomiale se situe en
lancers, plus un évènement aura une grande probabilité plus il sortira souvent. Cependant, il est rare qu'il sorte pour chaque lancer. En conséquence, le pic de probabilité de la loi binomiale se situe en ![E[(N+1)*p]](../pages_stat-theorie/equations_stat-theorie/equation118.png) , où
, où 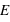 est la partie entière. Si p tend vers 1 alors le pic tendra vers
est la partie entière. Si p tend vers 1 alors le pic tendra vers 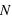 , à l'inverse il tendra vers 0. De plus, l'espérance de la loi binomiale vaut
, à l'inverse il tendra vers 0. De plus, l'espérance de la loi binomiale vaut 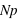 et son écart type vaut
et son écart type vaut 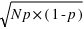 . Dans le cas ou
. Dans le cas ou 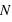 est très grand, un million par exemple, Le rapport écart-type sur espérance vaut
est très grand, un million par exemple, Le rapport écart-type sur espérance vaut 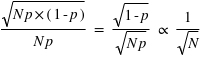 , il tend vers zéro. Si l'on voit l'espérance comme la mesure d'une observation et l'écart type comme son incertitude absolue alors, si
, il tend vers zéro. Si l'on voit l'espérance comme la mesure d'une observation et l'écart type comme son incertitude absolue alors, si 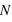 est très grand, l'incertitude relative sur la mesure sera très faible. Par exemple, dans un métal constitué de milliards d'atomes, supposons que les spins de chaque atome puissent être en haut ou en bas avec la même probabilité,
est très grand, l'incertitude relative sur la mesure sera très faible. Par exemple, dans un métal constitué de milliards d'atomes, supposons que les spins de chaque atome puissent être en haut ou en bas avec la même probabilité, 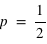 . Alors le métal n'aura pas de champ magnétique significatif car il aura statistiquement à chaque instant quasiment autant de spins en haut qu'en bas. La différence instantanée entre le nombre d'atomes ayant un spin en haut ou en bas, générateur d'un champ magnétique, sera en ordre de grandeur
. Alors le métal n'aura pas de champ magnétique significatif car il aura statistiquement à chaque instant quasiment autant de spins en haut qu'en bas. La différence instantanée entre le nombre d'atomes ayant un spin en haut ou en bas, générateur d'un champ magnétique, sera en ordre de grandeur 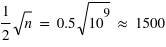 ; ce qui fournira des champs très faibles en comparaison du potentiel que pourraient produire les
; ce qui fournira des champs très faibles en comparaison du potentiel que pourraient produire les  atomes du métal si tous les spins étaient alignés dans le même sens. De plus, ce champ magnétique est très instable dans le temps (on dit qu'il fluctue) et a une moyenne nulle au cours du temps.
atomes du métal si tous les spins étaient alignés dans le même sens. De plus, ce champ magnétique est très instable dans le temps (on dit qu'il fluctue) et a une moyenne nulle au cours du temps.
La loi de Poisson
Loi de Poisson
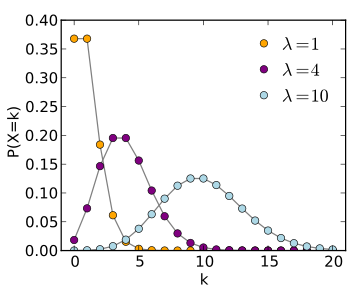
Trois exemples de loi de probabilité derivé de la loi de Poisson pour trois valeurs de
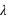
: 1, 4 et 10.
Crédit :
Wikipédia
Définition
La loi de Poisson, nommée d'après le mathématicien français Siméon Denis Poisson, s'applique à une variable discrète mais pouvant prendre des valeurs arbitrairement grandes. Son ensemble univers peut alors se confondre avec l'ensemble des entiers naturels. La loi de Poisson dépend d'un paramètre noté par usage 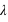 . La loi de probabilité de la loi de Poisson est
. La loi de probabilité de la loi de Poisson est 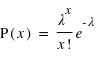 toujours positive (voir figure). Si
toujours positive (voir figure). Si 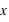 vaut 0, comme
vaut 0, comme 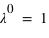 et
et 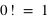 , alors
, alors 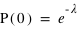 . Lorsque
. Lorsque  tend vers l'infini,
tend vers l'infini, 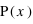 tend vers 0 du fait du terme en factorielle qui domine le terme
tend vers 0 du fait du terme en factorielle qui domine le terme 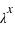 . Cette loi de probabilité admet un unique pic, appelé aussi mode, avec la valeur de
. Cette loi de probabilité admet un unique pic, appelé aussi mode, avec la valeur de 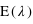 , si
, si 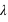 n'est pas un entier, et deux pics,
n'est pas un entier, et deux pics, 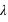 et
et 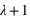 , si
, si 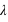 est un entier. L'espérance ainsi que la variance de cette fonction valent
est un entier. L'espérance ainsi que la variance de cette fonction valent 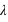 . L'écart type vaut donc
. L'écart type vaut donc 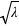 .
.
Bruit de photons
Il a déjà été fait mention dans la première partie de ce cours sur les statistiques des exoplanètes, que les photons captés pendant un temps 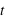 par un pixel de caméra CCD suivent une loi de Poisson. De ce fait, lorsque plusieurs poses du même objet astronomique sont faites, durant par exemple 10 minutes, le nombre de photons d'un pixel provenant de l'objet décrit une loi de Poisson dont la moyenne qui est la mesure physique est le paramètre de la loi.
par un pixel de caméra CCD suivent une loi de Poisson. De ce fait, lorsque plusieurs poses du même objet astronomique sont faites, durant par exemple 10 minutes, le nombre de photons d'un pixel provenant de l'objet décrit une loi de Poisson dont la moyenne qui est la mesure physique est le paramètre de la loi.
La loi normale
Loi normale
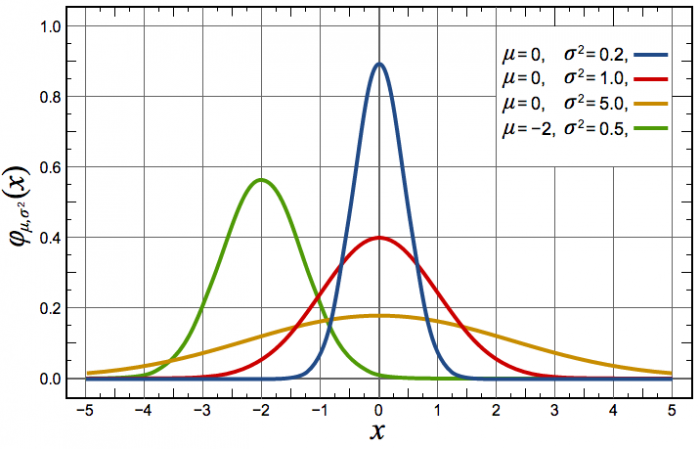
Trois exemples de fonctions de probabilités de loi normale avec différents espérances et écart-types.
Crédit :
Wikipédia
Fonction de distribution de la loi normale
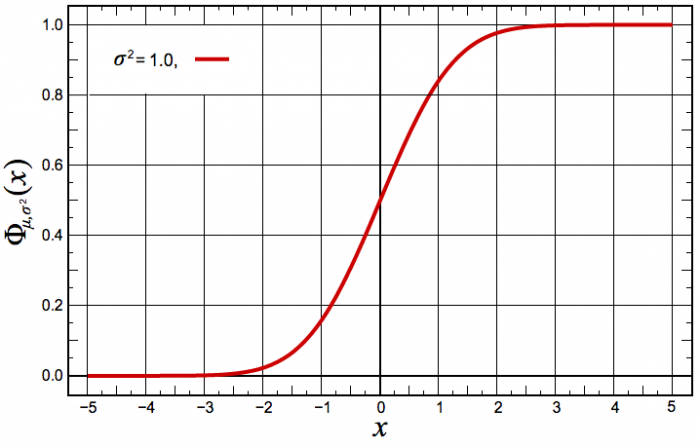
La fonction de distribution de la loi normale dont l'écart-type vaut 1 et l'espérance 0.
Crédit :
Wikipédia
Ecart-type de la loi normale
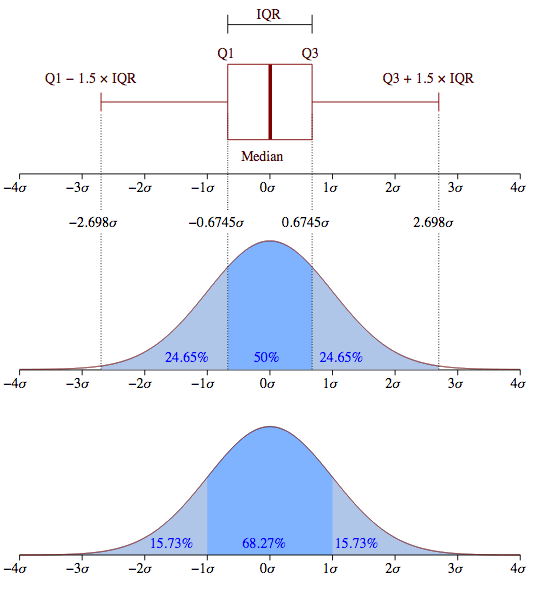
Figure du haut, boîte à moustaches représentant l'espace interquartile, les extrema théoriques étant à l'infini. Figure du milieu, la valeur exprimée en
des différents quartiles. Figure du bas, la probabilité d'avoir un résultat entre [
,
] (15,73 %), entre [
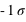
,
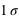
] (68,27 %) et enfin entre [
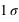
,
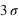
] (15,73 %).
Crédit :
Wikipédia
Définition
La dernière loi décrite est la plus connue si ce n'est la plus utilisée dans le domaine des statistiques. C'est le prolifique mathématicien allemand Carl Frierich Gauss qui la popularisa, elle porte son nom : la loi gaussienne aussi appelée loi normale. A l'inverse des deux précedentes lois, elle s'applique sur l'ensemble des réels. Pour un intervalle [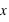 ,
, 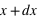 ], cette loi de probabilité vaut :
], cette loi de probabilité vaut : 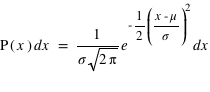 . Elle a deux paramètres qui sont
. Elle a deux paramètres qui sont 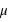 , l'espérance de la fonction de probabilité, et
, l'espérance de la fonction de probabilité, et 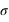 , l'écart type. Le terme devant l'exponentielle est un terme de normalisation afin que la probabilité totale de l'univers, donné par l'intégrale de cette loi depuis
, l'écart type. Le terme devant l'exponentielle est un terme de normalisation afin que la probabilité totale de l'univers, donné par l'intégrale de cette loi depuis 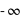 jusque
jusque 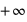 , vale 1. Le mode, valeur pour laquelle la fonction connaît un pic, est égale à sa moyenne,
, vale 1. Le mode, valeur pour laquelle la fonction connaît un pic, est égale à sa moyenne, 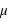 . L'écart-type à l'espérance est donné par
. L'écart-type à l'espérance est donné par 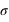 . A
. A 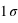 la probabilité chute d'une facteur
la probabilité chute d'une facteur 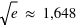 ; à
; à 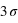 , ce facteur devient
, ce facteur devient 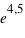 , soit un peu plus de 90. La chute est donc très rapide à mesure qu'on s'éloigne de la valeur moyenne. En d'autres termes, la probabilité de voir sortir un réel séparé de plus de
, soit un peu plus de 90. La chute est donc très rapide à mesure qu'on s'éloigne de la valeur moyenne. En d'autres termes, la probabilité de voir sortir un réel séparé de plus de 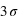 de la moyenne devient très faible, et cette probabilité devient quasiment nulle à
de la moyenne devient très faible, et cette probabilité devient quasiment nulle à 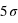 (voir la troisième figure).
(voir la troisième figure).
Une loi pour les erreurs de mesures
Lorsqu'une expérience est effectuée plusieurs fois, un résultat un peu différent de celui attendu apparaît. La différence entre la vraie valeur et notre mesure est appelée l'erreur. Par exemple, dans le cas de la fabrication de pièces mécaniques dans l'industrie, aucune pièce n'est strictement identique à une autre. Il y a donc un écart (une erreur) à la valeur désirée par le fabricant. Les causes des erreurs peuvent être multiples mais si elles sont sans lien entre elles (on dit qu'elles sont indépendantes), alors la loi de probabilité suivie par les erreurs est une gaussienne. Deux qualificatifs caractérisent une expérience ou la machine fabriquant une pièce mécanique : la fiabilité et la précision. La fiabilité informe si vous êtes en accord avec l'espérance en calculant la différence entre la moyenne obtenue et la valeur réelle. La précision quantifie l'incertitude pour chaque expérience, elle est donnée par l'écart-type, 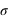 . Si la moyenne diffère significativement de l'espérance ("signifcativement" voulant dire "par rapport à l'écart-type"), on parle de mesure biaisée.
. Si la moyenne diffère significativement de l'espérance ("signifcativement" voulant dire "par rapport à l'écart-type"), on parle de mesure biaisée.
Exercices
Auteur: Sylvain Fouquet
Exercices
Ce chapitre a pour but de revoir et de tester les connaissances sur la théorie des probabilités. Quelques questions de cours rappellent les concepts clés, puis, des questions proches du cours en sont une application directe pour tester la bonne compréhension du concept. Ensuite, des exercices, supposant que le cours est bien appris et compris, utilisent les probabilités pour résoudre des problèmes particuliers.
Variables aléatoires
 Cours
Cours
Difficulté : ☆
Question 1)
Qu'est-ce qu'une variable aléatoire ?
La réponse est dans le cours.
Question 2)
Quels sont les deux types de variables aléatoires ?
La réponse se trouve dans le cours.
 Exercice sur les variables aléatoires
Exercice sur les variables aléatoires
Difficulté : ☆
Question 1)
Ayant deux dés distinguables, un bleu et un rouge, combien d'événements sont possibles en les lançant ? Notez bien que l'évènement "Face 1" pour le dé rouge et "Face 2" pour le dé bleu, noté (1,2), n'est pas le même événement que "Face 2" pour le dé rouge et "Face 1" pour le dé bleu, noté (2,1).
Pensez à bien énumérer toutes les combinaisons possibles, en se souvenant que l'univers pour l'ensemble des deux dés est donné par le produit cartésien des univers pour chacun des dés.
Question 2)
Même question avec deux dés rouges que l'on choisit de ne pas distinguer. En d'autres termes, les couples tels que (2, 1) et (1, 2) sont considérés comme un unique évènement.
Quels événements de la question précédente sont à présent confondus ? Sur quel critère ? Combien d'événements sont concernés ?
Question 3)
Supposons un générateur parfait de nombres aléatoires réels dans l'intervalle [0, 1[. Quels sont les évènements possibles et combien y en a-t-il ?
La variable aléatoire ainsi générée est-elle discrète ou continue ?
Question 4)
L'ordinateur n'est pas parfait et ne peut garder en mémoire que 4 chiffres après la virgule. Combien d'événements le générateur de la question 3) peut-il alors fournir ?
Pensez à énumérer tous les cas possibles, en gardant à l'esprit que l'ensemble des possibilités est donné par le produit cartésien des possibilités pour chaque décimale.
Ensemble
La théorie des probabilités se sert beaucoup de la théorie des ensembles. Ces exercices ont pour but de vous l'illustrer
 Cours sur les ensembles
Cours sur les ensembles
Question 1)
Définir l'union de deux ensembles A et B ? Quelle est alors la probabilité 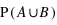 , le signe
, le signe 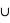 signifiant Union ?
signifiant Union ?
Une représentation graphique des ensembles A et B (dans le cas général où leur intersection est non vide) pourra être utile.
Question 3)
Quelle est la probabilité P(A U B U C) en fonction de P(A), P(B) et P(C) ?
Là encore, une représentation graphique des ensembles A, B, C et de leurs intersections sera très utile.
Question 4)
Définir le complémentaire de l'ensemble A. Quelle est alors sa probabilité par rapport à 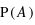 ?
?
Une représentation graphique de l'univers des possibles, de son sous-ensemble A et de son complémentaire peut être utile.
Probabilités à variables discrètes et équipartition
 Lancers de deux dés
Lancers de deux dés
Difficulté : ☆
Question 1)
Soit deux dés distincts que l'on lance, quels sont les différents événements et leurs probabilités ?
On pourra se reporter à l'exercice précédent.
Question 2)
On s'intéresse maintenant à la somme des deux dés. Quels sont les événements possibles et comment sont-ils liés aux événements de la question précédente ? De là, quelles sont leurs probabilités ?
Examiner les valeurs que prend la somme pour chaque événement décrit à la question précédente.
Question 3)
Commentez la nouvelle loi de probabilité calculée.
Reconnaît-on une loi du cours ? Donner les différentes caractéristiques observées sur cette loi (symétries éventuelles ?)
Question 4)
Vaut-il mieux tenter de faire un 6 avec un dé ou avec la somme de deux dés ?
 Jeu de fléchettes
Jeu de fléchettes
Difficulté : ☆☆
Question 1)
Soit un jeu de fléchettes avec une cible de rayon 10 cm. Quels événements considère-t-on en général dans ce jeu ? Sur quoi est basée la probabilité de ces derniers ?
Comment compte-t-on les points sur une cible de fléchettes ?
Question 2)
On suppose que la moitié des fléchettes n'atteint pas la cible et que la zone centrale donnant le plus de point a un rayon de 1 cm. Quelle est alors la probabilité de faire le maximum de points ?
Probabilités conditionnelles
 Faux positifs
Faux positifs
Difficulté : ☆☆
Lors du dépistage d'une maladie rare, touchant près d'une personne sur mille, les tests ne sont pas fiables à 100%. Après une campagne de dépistage, il y a alors des faux positifs, c'est-à-dire des personnes dépistées comme malades alors qu'elles sont saines. À l'inverse, il y a aussi des faux négatifs, c'est-à-dire des personnes dépistées comme saines mais en réalité malades. Le problème est alors de savoir quelle est la proportion de faux positifs parmi les détections.
On suppose qu'un patient malade est détecté par le dépistage avec une probabilité de 99%. À l'inverse, un patient sain est détecté comme tel avec une probabilité de 95%.
Question 1)
Quel est la malchance d'être diagnostiqué faux-positif, c'est à dire, quelle est la probabilité qu'une personne positive soit en fait non malade ?
Question 2)
Qu'en déduire sur le résultat d'un test positif ? Comment expliquer cela ?
Fonction de distribution
 Cours
Cours
Difficulté : ☆
Question 2)
Définir la fonction de distribution d'une loi de probabilité.
Question 3)
Quelle est la fonction de distribution de la loi de probabilité : 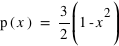 pour x dans l'intervall [0, 1], et
pour x dans l'intervall [0, 1], et 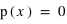 en dehors.
en dehors.
Utiliser la définition mathématique de la fonction de distribution par rapport à celle de la loi de probabilité correspondante.
Propriétés et applications de la loi binomiale
 Loi binomiale
Loi binomiale
Difficulté : ☆
Question 1)
Définir la loi de probabilité binomiale ? Quelles sont ces propriétés : espérance et écart-type ?
Question 2)
Pour des événements de 30 lancers d'une pièce de monnaie non biaisée, combien de combinaisons présentent 28 lancers "face" ? Combien présentent 13 lancers "pile" ?
Penser aux fonctions mathématiques de dénombrement vues en cours.
Question 3)
Si la probabilité d'avoir pile vaut 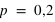 , quelles sont alors les probabilités d'avoir 28 faces ou 13 piles ?
, quelles sont alors les probabilités d'avoir 28 faces ou 13 piles ?
Utiliser la définition de la loi binomiale.
Propriétés et applications de la loi poissonnienne
 Loi de Poisson
Loi de Poisson
Difficulté : ☆
Question 1)
Définir la loi de probabilité de Poisson ? Quelles sont ses propriétés : espérance et écart-type ?
Question 2)
Soit un champ de 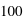 m², il tombe des gouttes de pluie en 10 secondes suivant une loi de Poisson de paramètre
m², il tombe des gouttes de pluie en 10 secondes suivant une loi de Poisson de paramètre 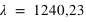 . Combien en moyenne, tombera-t-il de gouttes d'eau dans ce champ en 1 heure ?
. Combien en moyenne, tombera-t-il de gouttes d'eau dans ce champ en 1 heure ?
Utiliser la réponse à la question précédente.
Propriétés et applications de la Gaussienne
 Loi Normale
Loi Normale
Difficulté : ☆
Question 1)
Définir la loi de probabilité normale ? Quelles sont ses propriétés : espérance et écart-type ?
Question 2)
Pour une loi normale de moyenne nulle, quelles sont les probabilités d'avoir, un résultat en dehors de 1 ou 3  (
( étant l'écart-type) ?
étant l'écart-type) ?
Utiliser les valeurs tabulées de la fonction de distribution associées à la loi normale se trouvant sur la figure du cours.
Question 3)
Supposons qu'un modèle physique prédise une mesure théorique de 20 mètres lors d'une expérience. L'expérimentateur fait l'expérience et trouve 19,5 mètres. Que dire sur le modèle physique selon que l'incertitude est de 0,5 m ou de 0,05 m ?
Réfléchir en termes d'interprétation statistique selon une loi normale, en supposant la mesure non biaisée (c'est-à-dire que la moyenne des valeurs mesurées tend vers la valeur théorique quand le nombre de mesures s'accroît).
Mini-projet
Auteur: Sylvain Fouquet
Mini-projet
Dans cette dernière partie du cours, un ensemble d'exercices fait une synthèse entre la statistique des exoplanètes et les lois de probabilité. Les cinq exercices utilisent les lois de probabilité pour réfléchir sur les exoplanètes. Il faut noter que les hypothèses faites dans les énoncés (distribution des planètes autour d'une étoile donnée, détectabilités des exoplanètes) sont des hypothèses ad hoc. Ces propriétés sont encore très mal connues.
Contrôle
 Combien d'exoplanètes dans la Voie Lactée ?
Combien d'exoplanètes dans la Voie Lactée ?
La première question concerne le nombre d'exoplanètes dans les sytèmes planétaires de notre galaxie, la Voie Lactée, en comparaison des planètes du système solaire. Notez que jusqu'à ce jour, on ne détecte que les exoplanètes de la Voie Lactée. On ne sait rien des planètes des milliards d'autres galaxies connues.
Supposons que la Voie Lactée soit constituée de 100 milliards d'étoiles, ce qui est juste au première ordre. Supposons aussi que la probabilité de trouver des planètes autour d'une étoile soit la même pour chaque étoile. Ceci est sûrement faux mais simplifie les calculs. Enfin supposons que la loi de probabilité du nombre de planètes par étoile est une loi de Poisson ayant un paramètre  égal à 5.
égal à 5.
Question 1)
Combien en moyenne y a-t-il d'exoplanètes autour des étoiles ? Quelle est la probabilité de trouver un système planétaire avec un nombre égal à la moyenne ?
Question 2)
Quel est la probabilité de trouver un système planétaire tel que le système solaire, avec huit planètes ou avec au moins huit planètes ? Que conclure sur le système solaire dans ce cas ?
Question 3)
Considérant les données observationnelles, la plupart des exoplanètes sont seules autour de leur étoile. Dans ce cas, la loi des grands nombres tendrait à montrer que la moyenne des exoplanètes par étoiles serait proche de 1. Que devient la chance de trouver un système solaire dans un tel cas. Quelle est l'erreur de raisonnement fait ici ?
Question 4)
Combien statistiquement devrait-il y avoir d'exoplanètes dans la Voie Lactée ?
 Les Jupiter Chauds
Les Jupiter Chauds
Cet exercice porte sur les Jupiter Chauds, des exoplanètes ayant une masse similaire à celle de Jupiter et très proches de leur étoile. Outre leur intérêt physique qui obligent à repenser la formation et l'évolution des planètes, ces planètes sont aussi intéressantes d'un point de vue statistique, car elles sont plus faciles à détecter et donc moins sujettes aux biais observationnels. Cet exercice montre que même avec une faible fraction de Jupiter Chauds dans la galaxie, cette population peut paraître la plus importante avec des moyens obervationnels limités.
Supposons toujours que les étoiles ont toute la même loi de probabilité d'avoir des planètes, un loi de Poisson avec une moyenne de 5. Supposons que la probabilité pour une planète d'être un Jupiter Chaud soit de 0,0001. Supposons que l'on soit sûr de pouvoir les découvrir à une distance de 2 kpc. On suppose aussi que la probabilité qu'une planète soit de type Terre est de 0,1 mais qu'il n'est possible de la trouver qu'à moins de 50 parsec.
Question 1)
Quelle loi de probabilité va servir pour déterminer le nombre de Jupiter Chauds ou de planètes de type Terre par la suite?
Question 2)
Combien de Jupiter Chauds et de planètes de type Terre y aurait-il dans la Voie Lactée ? Quel est leur rapport ?
Question 3)
En sélectionnant 100 000 étoiles brillantes dans le ciel, toutes à moins de 2 kpc, dont 27 sont à moins de 50 parsec, combien statistiquement y aura-t-il de Jupiter Chauds et de planètes de type Terre découverts? Quel est leur rapport ? Conclure.
 Relation étoiles-exoplanètes
Relation étoiles-exoplanètes
Cet exercice s'intéresse aux relations qui pourraient exister entre les exoplanètes et leur étoile hôte. La théorie bayésienne est alors utilisée. Dans un vision plus réaliste des exoplanètes que pour les exercices précédents, la probabilité de présence de planètes n'est pas la même pour les différents types d'étoiles.
Question 1)
Lors d'une observation non biaisée, c'est à dire complète, pour détecter des planètes géantes gazeuses sur 200 étoiles, 28 planètes géantes gazeuses sont découvertes autour de 75 étoiles de métallicité plus grande que 0 (étoiles riches en métaux) et seulement 2 pour les 125 étoiles de métallicité plus petite que 0 (étoiles pauvres en métaux). A chaque fois, les planètes gazeuses géantes sont trouvées seules sans autre géante gazeuse. Que dire qualitativement de l'influence de la métallicité sur la détection de planètes gazeuses?
Question 2)
Soit, G, l'ensemble des étoiles ayant la propriété suivante "avoir une seule planète gazeuse pour une étoile" et son contraire NG ainsi que l'ensemble M ="avoir une étoile riche en métaux" et son contraire NM. Avec les données de l'énoncé, quelles sont les probabilités de P(G), P(NG), P(M), P(NM) ?
Question 3)
Que signifient les probabilité suivantes P(G|M) et P(G|NM) ? Quelles sont leurs valeurs ? Les comparer à P(G) et commenter.
Question 4)
Pour une étoile choisie au hasard, une unique planète géante gazeuse est observée. Qu'elle est la probabilité pour l'étoile d'être une étoile riche en métaux, P(M|G) ? Commenter.
Question 5)
Comparer la probabilité que l'étoile avait d'être riche en métaux avant et après la découverte de la planète géante gazeuse. Quels sont les points forts et les points faibles de cette méthode pour connaître la métallicité d'une étoile ?
 Détection d'une exoplanète par transit
Détection d'une exoplanète par transit
Transit d'exoplanètes
Différentes configurations de transit d'exoplanète. La direction de la ligne de visée est indiquée à droite. De la gauche vers la droite: une orbite d'exoplanète ayant un angle nul avec la ligne de visée, il y a un transit assuré, ensuite une exoplanète dont l'orbite fait un angle de quelques degrés, noté alpha, avec la ligne de visée, enfin une exoplanète dont l'orbite est perpendiculaire à la ligne de visée, l'exoplanète n'est alors pas visible par transit.
Crédit :
Sylvain Fouquet
Lors d'un transit, une exoplanète passe devant son étoile depuis un observateur sur terre, la luminosité de l'étoile est alors diminuée durant un certain laps de temps avant de revenir à la normale. Cette mesure permet la détection d'une exoplanète. Lorsqu'une exoplanète est recherchée par la méthode des transits, les observateurs espèrent que cette l'orbite de l'exoplanète passe devant l'étoile hôte pour un observateur terrestre. Il y a un facteur chance pour détecter des transits d'une étoile donnée. Les campagnes de recherche observent un grand nombre d'étoiles et l'analyse des données nécessite de corriger le taux de détection de transits de la probabilité d'observer ces transits.
Question 1)
Supposons qu'une étoile ait un rayon de 1 million de km (par comparaison le Soleil fait près de 700 000 km de rayon), quel angle maximal, sur le plan d'une trajectoire circulaire d'une exoplanète à 1 U.A., faut-il pour voir un transit? Notons qu' une inclinaison de 0 degré signifie que la trajectoire est vue de côté, donc qu'il y a un transit, et qu'une inclinaison de 90 degrés signifie que la trajectoire est vue de face, donc sans transit.
Question 2)
Que dire sur l'influence du rayon de l'étoile et de la distance de l'exoplanète à cette étoile sur l'angle minimal requis pour détecter l'exoplanète ? Commenter le biais de cette méthode.
Question 3)
Que se passe-t-il qualitativement si l'orbite n'est plus circulaire mais elliptique ? Commenter sur un autre biais de la méthode des transits.
Question 4)
Dans le cas précédent (une exoplanète à 1 U.A. d'une étoile de rayon 1 millions de km), quelle est la probabilité de la détecter, sachant qu'aucun angle n'est a priori préféré pour son orbite circulaire ?
Question 5)
Que devient cette probabilité pour un Jupiter Chaud (distant de son étoile de 0.1 U.A) autour d'une étoile géante ayant un rayon de 10 millions de km ?
Conclusion
Au fil de ce cours plusieurs concepts clés sur la théorie des probabilités ont été étudiés. Premièrement, il y a eu l'idée de variables aléatoires qui signifie que pour la même expérience les résultats sont différents. Il peut y en avoir un nombre fini, comme pour le lancer d'un dé, ou infini comme pour le temps entre deux averses. Ensuite, l'idée qu'à chaque résultat ou évènement, il est possible d'associer une probabilité allant de 0, l'impossibilité, à 1, la certitude. Enfin, quatre lois de probabilités très utilisées ont été présentées : la loi d'équipartition lorsque tous les évènements ont la même probabilité, la loi binomiale, la loi de Poisson et la loi Normale.
Quant à la statistique, elle est en pratique utilisée pour découvrir ces lois de probabilités. Dans ce cours, le support a été l'étude des exoplanètes. L'étude d'un échantillon a montré des propriétés sur la masse, le rayon ainsi que le péricentre des exoplanètes.
Ce cours n'est évidemment qu'une introduction aux probabilités. Une étude plus approfondie permettra de mieux comprendre la définition mathématique rigoureuse des probabilités. De plus, avec le couple probabilité-statistique, il est possible de tester différentes lois de probabilité et de les confronter à des données statistiques pour en déduire si la loi à de fortes chances d'être correcte ou est sûrement fausse. Cela se fait par l'utilisation de tests statistiques, tels que le test Kolmogorov-Smirnov. Les probabilités servent aussi à ajuster des courbes ou des modèles. Cela se fait avec le test dit du "chi2" pour 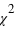 . Ce ne sont ici que des exemples très connus mais le couple probabilité-statistique est bien plus riche et peut servir dans bons nombres de domaines scientifiques et même économiques.
. Ce ne sont ici que des exemples très connus mais le couple probabilité-statistique est bien plus riche et peut servir dans bons nombres de domaines scientifiques et même économiques.
-------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------FIN DU CHAPITRE -------------
ACCES AU PLAN DES CHAPITRES
Réponses aux exercices
pages_stat-exercice/variable.html
Exercice
'Cours'
- Question 1
Aide :
La réponse est dans le cours.
Solution :
Une variable aléatoire est une variable dont la réalisation (valeur numérique par exemple) change à chaque mesure de façon aléatoire.
- Question 2
Aide :
La réponse se trouve dans le cours.
Solution :
Ce sont les variables aléatoires discrètes (l'ensemble des valeurs possibles de la variable est dénombrable) et les variables aléatoires continues (pour lesquelles l'ensemble des valeurs possibles n'est pas dénombrable).
pages_stat-exercice/variable.html
Exercice
'Exercice sur les variables aléatoires'
- Question 1
Aide :
Pensez à bien énumérer toutes les combinaisons possibles, en se souvenant que l'univers pour l'ensemble des deux dés est donné par le produit cartésien des univers pour chacun des dés.
Solution :
Il y a 6 possibilités d'évènements pour le dé rouge : {1, 2, 3, 4, 5, 6}. Pour chacun de ces évènements, il y en a six autres pour le dé bleu. Donc le nombre total d'évènements est 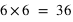 . Une façon plus détaillée de le comprendre est de dire qu'un évènement est le couple des résultats du dé rouge et du dé bleu (Rouge, Bleu). Les couples sont donc (1, 1), (1, 2), (1, 3), (1, 4), ... On retrouve qu'il y a 6 possibilités pour le premier membre du couple et 6 pour l'autre, cela donne 36 possibilités.
. Une façon plus détaillée de le comprendre est de dire qu'un évènement est le couple des résultats du dé rouge et du dé bleu (Rouge, Bleu). Les couples sont donc (1, 1), (1, 2), (1, 3), (1, 4), ... On retrouve qu'il y a 6 possibilités pour le premier membre du couple et 6 pour l'autre, cela donne 36 possibilités.
- Question 2
Aide :
Quels événements de la question précédente sont à présent confondus ? Sur quel critère ? Combien d'événements sont concernés ?
Solution :
Dans ce cas, une méthode lente mais sûre est de lister tous les couples possibles en commençant par tous ceux qui ont le nombre 1 pour le premier dé, puis ceux qui reste avec le 2, ensuite le 3 et ainsi de suite : (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 3), (3, 4), (3, 5), (3, 6), (4, 4), (4, 5), (4, 6), (5, 5), (5, 6), (6, 6). Il est facile de remarquer qu'il y a six couples avec le nombre 1 puis 5 avec le 2 sans réintroduire les couples déjà vus avec le chiffre 1, puis 4, 3, 2, et enfin 1 couple possible avec le chiffre 6 qui est (6,6). Le nombre total de couples est 6+5+4+3+2+1 = 21.
Une autre façon plus rapide de calculer le nombre d'évènements est de repartir du résultat de la question précédente. Sur les 36 couples, seuls les couples avec deux nombres différents peuvent être confondus lorsque les dés sont de la même couleur, par exemple (2, 1) avec (1, 2). Cependant les couples (1, 1), (2, 2), ...(6, 6) ne peuvent pas être confondus avec d'autres. Donc sur les 36 évènements, 30 sont confondables. Chacun de ces 30 cas ne peut être confondu qu'avec un autre couple. (3, 1) n'est confondable qu'avec (1, 3). Sur les 30 évènements, il y en a donc deux fois trop. En résumé, il reste les 6 évènements non confondables et les 15 confondables, on retrouve bien les 21 évènements.
- Question 3
Aide :
La variable aléatoire ainsi générée est-elle discrète ou continue ?
Solution :
Les évènements possibles sont tous les nombres réels allant de 0 inclus à 1 non inclus. Il y en a donc une infinité non dénombrable.
- Question 4
Aide :
Pensez à énumérer tous les cas possibles, en gardant à l'esprit que l'ensemble des possibilités est donné par le produit cartésien des possibilités pour chaque décimale.
Solution :
Pour chacune des quatre décimales, le générateur peut fournir 10 chiffres allant de 0 à 9, donc il y a donc 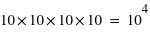 évènements. Le premier est 0,0000 puis 0,0001 etc. et le dernier est 0,9999.
évènements. Le premier est 0,0000 puis 0,0001 etc. et le dernier est 0,9999.
pages_stat-exercice/ensemble.html
Exercice
'Cours sur les ensembles'
- Question 1
Aide :
Une représentation graphique des ensembles A et B (dans le cas général où leur intersection est non vide) pourra être utile.
Solution :
L'ensemble C, défini comme l'union de A et B ( ) se définit comme l'ensemble contenant les éléments se trouvant dans A ou dans B. On a alors
) se définit comme l'ensemble contenant les éléments se trouvant dans A ou dans B. On a alors 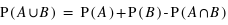 où le symbole
où le symbole  désigne l'intersection.
désigne l'intersection.
- Question 2
Aide :
Une représentation graphique des ensembles A et B (dans le cas général où leur intersection est non vide) pourra être utile.
Solution :
L'ensemble 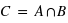 se définit comme l'ensemble contenant les éléments se trouvant dans A etdans B. L'ensemble
se définit comme l'ensemble contenant les éléments se trouvant dans A etdans B. L'ensemble 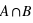 étant par conséquent inlcus dans A et B, sa probabilité sera inférieure ou égale à la probabilité de chacun de ces deux ensembles :
étant par conséquent inlcus dans A et B, sa probabilité sera inférieure ou égale à la probabilité de chacun de ces deux ensembles : 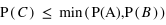 . Dans un jeu de 52 cartes, si A est l'ensemble des cartes rouges et B l'ensemble des cartes noires alors
. Dans un jeu de 52 cartes, si A est l'ensemble des cartes rouges et B l'ensemble des cartes noires alors 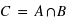 est l'ensemble vide, d'où
est l'ensemble vide, d'où 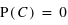 .
.
- Question 3
Aide :
Là encore, une représentation graphique des ensembles A, B, C et de leurs intersections sera très utile.
Solution :
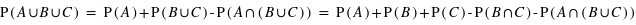 Or
Or 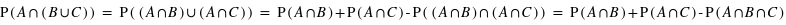 Donc
Donc 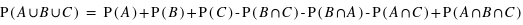
- Question 4
Aide :
Une représentation graphique de l'univers des possibles, de son sous-ensemble A et de son complémentaire peut être utile.
Solution :
L'ensemble C, complémentaire de A se définit comme l'ensemble contenant tous les éléments qui ne se trouvent pas dans A. Par exemple, si l'ensemble A se définit par les coeurs dans un jeu de cartes, l'ensemble opposé de A, noté  , se définit comme tout ce qui n'est pas coeur : pique, trèfle et carreau. Il est parfois plus simple de définir un ensemble par ce qu'il n'est pas plutôt que par ce qu'il est. De là, le principe du tiers exclu donne
, se définit comme tout ce qui n'est pas coeur : pique, trèfle et carreau. Il est parfois plus simple de définir un ensemble par ce qu'il n'est pas plutôt que par ce qu'il est. De là, le principe du tiers exclu donne  , l'univers des possibles. Or
, l'univers des possibles. Or 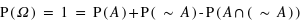 . Comme cette dernière intersection est vide, on a
. Comme cette dernière intersection est vide, on a 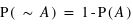 .
.
pages_stat-exercice/proba-discrete.html
Exercice
'Lancers de deux dés'
- Question 1
Aide :
On pourra se reporter à l'exercice précédent.
Solution :
Cette question est déjà vue à la question sur les variables aléatoires. Il y a 36 possibilités qui se définissent par un couple de deux nombres (a, b) où a et b peuvent prendre toutes les valeurs de 1 à 6. Si les dés ne sont pas faussés, chaque événement aura la même probabilité donc 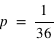
- Question 2
Aide :
Examiner les valeurs que prend la somme pour chaque événement décrit à la question précédente.
Solution :
Les événements possibles de sommes sont les nombres de 2 à 12. La preuve en est la liste exhaustive :
- (1, 1) = 2 ; 1 possibilité : Probabilité = 1/36 = 0.02777
- (1, 2) (2, 1) = 3 ; 2 possibilités : Probabilité = 2/36 = 1/18 = 0.05555
- (1, 3) (2, 2) (3, 1) = 4 ; 3 possibilités : Probabilité = 3/36 = 1/12 = 0.08333
- (1, 4) (2, 3) (3, 2) (4, 1) = 5 ; 4 possibilités : Probabilité = 4/36 = 1/9 = 0.11111
- (1, 5) (2, 4) (3, 3) (4, 2) (5, 1) = 6 ; 5 possibilités : Probabilité = 5/36 = 0.1388
- (1, 6) (2, 5) (3, 4) (4, 3) (5, 2) (6, 1) = 7 ; 6 possibilités : Probabilité = 6/36 = 1/6 = 0.16666
- (2, 6) (3, 5) (4, 6) (5, 3) (6, 2) =8 ; 5 possibilités : Probabilité = 5/36 = 0,13888
- (3, 6) (4, 5) (5, 4) (6, 3) = 9 ; 4 possibilités : Probabilité = 4/36 = 0,1111
- (4, 6) (5, 5) (6, 4) = 10 ; 3 possibilités : Probabilité = 3/36 = 0,083333
- (5, 6) (6, 5) = 11 ; 2 possibilités : Probabilité = 2/36 = 0.05555
- (6, 6) = 12 ; 1 possibilités : Probabilité = 1/36 = 0.027777
Cette liste donne les combinaisons pour toutes les sommes de deux dés. En utilisant la loi 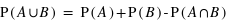 , il est alors possible de calculer la probabilité pour chaque valeur possible de la somme (de 2 à 12). Comme les évènements sont par nature disjoints l'un de l'autre,
, il est alors possible de calculer la probabilité pour chaque valeur possible de la somme (de 2 à 12). Comme les évènements sont par nature disjoints l'un de l'autre, 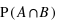 est toujours nulle. De ce fait, pour avoir la probabilité, il suffit de prendre le nombre total de combinaisons donnant la même valeur pour la somme, et de diviser ce nombre par 36.
est toujours nulle. De ce fait, pour avoir la probabilité, il suffit de prendre le nombre total de combinaisons donnant la même valeur pour la somme, et de diviser ce nombre par 36.
- Question 3
Aide :
Reconnaît-on une loi du cours ? Donner les différentes caractéristiques observées sur cette loi (symétries éventuelles ?)
Solution :
Cette loi, de forme "triangulaire", n'est pas équiprobable : la probabilité d'avoir une somme valant 3 n'est pas la même que d'avoir une somme valant 9. Cette loi présente un maximum pour la valeur 7 qui est la valeur la plus probable. Cette loi est symétrique par rapport à 7 car pour tout entier 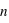 compris entre 2 et 12,
compris entre 2 et 12, 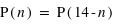 .
.
- Question 4
Solution :
La probabilité de faire un 6 avec un dé vaut 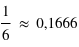 , et celle de faire une somme valant 6 avec deux dés est
, et celle de faire une somme valant 6 avec deux dés est 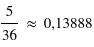 , comme vu à la question précédente. Donc il vaut mieux prendre un seul dé pour espèrer faire un 6.
, comme vu à la question précédente. Donc il vaut mieux prendre un seul dé pour espèrer faire un 6.
pages_stat-exercice/proba-discrete.html
Exercice
'Jeu de fléchettes'
- Question 1
Aide :
Comment compte-t-on les points sur une cible de fléchettes ?
Solution :
Dans le jeu de fléchettes, les événements sont l'ensemble des positions que peut atteindre la fléchette. Il y a l'extérieur de la cible qui vaut généralement 0 point et des zones à l'intérieur de la cible. Chaque zone de la cible a une surface bien définie. C'est l'étendue de cette surface qui détermine la probabilité de la toucher. Pour un joueur sans aucun talent pour viser, la probabilité de toucher une zone est proportionnelle à sa surface.
- Question 2
Solution :
La probabilité de toucher la cible est 1 moins "la probabilité de ne pas toucher la cible", car ces deux ensembles sont complémentaires. Donc la probabilité de toucher la cible vaut 0,5. En outre, la surface du centre vaut 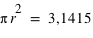 cm2 et celle de la cible tout entière vaut
cm2 et celle de la cible tout entière vaut 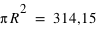 cm2. Or, la probabilité est proportionnelle à la surface, donc la probabilité de toucher la zone centrale, sachant que l'on a touché la cible, est P(toucher la cible)
cm2. Or, la probabilité est proportionnelle à la surface, donc la probabilité de toucher la zone centrale, sachant que l'on a touché la cible, est P(toucher la cible)  P(toucher la zone centrale | toucher la cible)
P(toucher la zone centrale | toucher la cible) 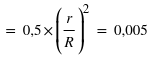 .
.
pages_stat-exercice/bayes.html
Exercice
'Faux positifs'
- Question 1
Solution :
La probabilité P(non malade | positif) = P(positif | non malade)  P(non malade) / P(positif). La probabilité d'être non malade est P(non malade) = 0,999 d'après l'énoncé. La probabilité d'être positif mais en étant non malade est P(positif | non malade) = 5% = 0,05, toujours d'après l'énoncé. Il reste le plus difficile, la probabilité d'être dépisté positif, qui est la somme entre les cas (disjoints) "malades" et "non malades" : P(positif) = P(positif | malade)
P(non malade) / P(positif). La probabilité d'être non malade est P(non malade) = 0,999 d'après l'énoncé. La probabilité d'être positif mais en étant non malade est P(positif | non malade) = 5% = 0,05, toujours d'après l'énoncé. Il reste le plus difficile, la probabilité d'être dépisté positif, qui est la somme entre les cas (disjoints) "malades" et "non malades" : P(positif) = P(positif | malade)  P(malade) + P(positif | non malade)
P(malade) + P(positif | non malade)  P(non malade) = 0,99
P(non malade) = 0,99 0,001 + 0,05
0,001 + 0,05 0,999 = 0,00099 + 0,04995 = 0,05094. En définitif, la probabilité d'être faux-positif est P(non malade | positif) = 0,05
0,999 = 0,00099 + 0,04995 = 0,05094. En définitif, la probabilité d'être faux-positif est P(non malade | positif) = 0,05  0,999 / 0,05094
0,999 / 0,05094  0,98. Donc 98% des patients étant déclarés malades sont en réalité sains.
0,98. Donc 98% des patients étant déclarés malades sont en réalité sains.
- Question 2
Solution :
Ce résultat, qui paraît absurde car le dépistage est censément très fiable, est dû au fait que le nombre de personnes saines est bien plus grand que celui des personnes malades. Donc, même si l'erreur est faible, cela touche un bien plus grand nombre de gens et donc révèle plus de faux malades que de vrais. Sur 1000 personnes, il ne devrait y avoir en moyenne qu'une personne malade car P(malade) = 0,1% de 1000, soit 1. Cependant en moyenne, le test en montre 50 de plus car P(positif|non malade) = 5% de 1000, soit 50.
pages_stat-exercice/fdd.html
Exercice
'Cours'
pages_stat-exercice/prop-binomiale.html
Exercice
'Loi binomiale'
pages_stat-exercice/prop-poissonnienne.html
Exercice
'Loi de Poisson'
- Question 1
Aide :
Voir cours.
Solution :
Pour une loi de Poisson de paramètre 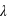 ,
, 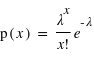 ,
,  et
et 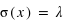
- Question 2
Aide :
Utiliser la réponse à la question précédente.
Solution :
En 10 secondes, il tombe en moyenne 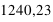 gouttes. Comme en une heure, il y a 360 fois 10 secondes, donc en 1 heure, il tombe en moyenne 446482,8 gouttes.
gouttes. Comme en une heure, il y a 360 fois 10 secondes, donc en 1 heure, il tombe en moyenne 446482,8 gouttes.
pages_stat-exercice/prop-gaussienne.html
Exercice
'Loi Normale'
- Question 1
Aide :
Voir cours.
Solution :
Pour une loi normale d'espérance 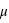 et d'écart-type
et d'écart-type 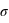 , on a
, on a 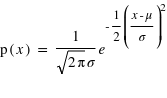
- Question 2
Aide :
Utiliser les valeurs tabulées de la fonction de distribution associées à la loi normale se trouvant sur la figure du cours.
Solution :
La probabilité d'avoir un résultat en dehors de 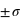 est donnée avec la loi de distribution :
est donnée avec la loi de distribution : 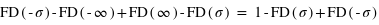 .
En regardant le cours, on calcule que la probabilité est d'environ 0,3173 en dehors de
.
En regardant le cours, on calcule que la probabilité est d'environ 0,3173 en dehors de  et d'environ 0,0027 en dehors de
et d'environ 0,0027 en dehors de 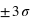 .
.
- Question 3
Aide :
Réfléchir en termes d'interprétation statistique selon une loi normale, en supposant la mesure non biaisée (c'est-à-dire que la moyenne des valeurs mesurées tend vers la valeur théorique quand le nombre de mesures s'accroît).
Solution :
Lors d'une expérience, la mesure est toujours entachée d'une erreur du fait qu'il est impossible de refaire exactement la même mesure. Une mesure suit généralement une loi normale où l'espérance est la mesure attendue et l'écart-type est l'incertitude. Dans notre cas, l'espérance est de 20 mètres. Si l'écart-type attendu par l'expérimentateur est de 0,5 m alors la valeur mesuré de 19,5 est à 1  de la valeure théorique. Cela est probable (31,73% de chance, voir question ci-dessus) ; la théorie ne semble pas fausse. Par contre si l'écart-type attendu est 0,05 alors la mesure est à 10
de la valeure théorique. Cela est probable (31,73% de chance, voir question ci-dessus) ; la théorie ne semble pas fausse. Par contre si l'écart-type attendu est 0,05 alors la mesure est à 10  . A trois
. A trois  , la probabilité est déjà faible (0,0027) mais à 10
, la probabilité est déjà faible (0,0027) mais à 10  elle est infinitésimale. La théorie semble alors invalidée par l'expérience.
elle est infinitésimale. La théorie semble alors invalidée par l'expérience.

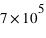
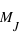 et 47
et 47 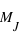 ; la Terre faisant par comparaison
; la Terre faisant par comparaison 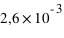
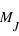 . Les masses sont données dans l'unité de la masse de Jupiter,
. Les masses sont données dans l'unité de la masse de Jupiter, 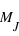 , qui fait
, qui fait 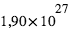 kg ou 317,8 masses terrestres . Ce premier critère statistique montre que la masse des planètes découvertes varie sur près de six ordres de grandeur. Cela ne prouve en aucun cas qu'il n'existe pas de planètes plus ou moins massives.
kg ou 317,8 masses terrestres . Ce premier critère statistique montre que la masse des planètes découvertes varie sur près de six ordres de grandeur. Cela ne prouve en aucun cas qu'il n'existe pas de planètes plus ou moins massives.
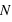 , est impair la valeur de la
médiane est celle de la
, est impair la valeur de la
médiane est celle de la 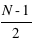 ème masse. Si le nombre de masse est pair, la médiane se calcule par la moyenne de la
ème masse. Si le nombre de masse est pair, la médiane se calcule par la moyenne de la 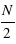 et
et 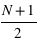 ème masses. Dans le cas des 1795 exoplanètes découvertes, seules 1032 ont une masse mesurée ; un nombre pair, donc la médiane correspond à la moyenne des masses des exoplanètes numéros 1032/2 = 512 et (1032+1)/2 = 513 qui est la masse 0,96
ème masses. Dans le cas des 1795 exoplanètes découvertes, seules 1032 ont une masse mesurée ; un nombre pair, donc la médiane correspond à la moyenne des masses des exoplanètes numéros 1032/2 = 512 et (1032+1)/2 = 513 qui est la masse 0,96  .
.
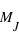 ) ou le dernier quart, nommée dernier quartile (2,75
) ou le dernier quart, nommée dernier quartile (2,75 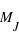 ) de l'échantillon. Pour un échantillon de taille
) de l'échantillon. Pour un échantillon de taille 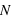 , le premier quartile se calcule en prenant la valeur
, le premier quartile se calcule en prenant la valeur 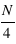 , si
, si 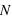 est un multiple de 4, ou la valeur de l'entier supérieur. Pour le dernier quartile, c'est la même méthode mais en utilisant
est un multiple de 4, ou la valeur de l'entier supérieur. Pour le dernier quartile, c'est la même méthode mais en utilisant 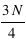 . L'écart entre le premier et le dernier quartile est nommé l'écart interquartile.
. L'écart entre le premier et le dernier quartile est nommé l'écart interquartile.

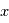 pour un échantillon de taille
pour un échantillon de taille 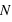 est :
est :
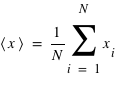
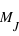 , très proche de la médiane à 2,75
, très proche de la médiane à 2,75 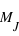 .
.
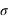 qui se définit par la moyenne des distances à la valeur moyenne. Il faut donc calculer tout d'abord toutes les distances au carré (le carré pour avoir des distances positives), de la moyenne à chaque valeur de l'échantillon,
qui se définit par la moyenne des distances à la valeur moyenne. Il faut donc calculer tout d'abord toutes les distances au carré (le carré pour avoir des distances positives), de la moyenne à chaque valeur de l'échantillon, 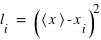 . La moyenne de
. La moyenne de 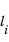 donne le carré de
donne le carré de 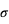 :
:

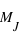 . Cela est presque deux fois plus grand que l'écart interquartile.
. Cela est presque deux fois plus grand que l'écart interquartile.

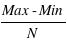 est trop petite, il n'y aura qu'un ou bien zéro élément de l'échantillon dans chaque intervalle. A l'inverse si les intervalles sont trop grands, il ne sera plus possible de distinguer les pics dans la distribution. Un bon choix pour le nombre d'intervalles est important. Si, par exemple, on divise le nombre total d'éléments de l'échantillon par N = 10, et que la distribution est uniforme, chaque intervalle devrait avoir à peu près 10 représentants.
est trop petite, il n'y aura qu'un ou bien zéro élément de l'échantillon dans chaque intervalle. A l'inverse si les intervalles sont trop grands, il ne sera plus possible de distinguer les pics dans la distribution. Un bon choix pour le nombre d'intervalles est important. Si, par exemple, on divise le nombre total d'éléments de l'échantillon par N = 10, et que la distribution est uniforme, chaque intervalle devrait avoir à peu près 10 représentants.
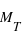 , la masse de la Terre, et
, la masse de la Terre, et 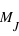 , la masse de Jupiter. L'histogramme des masses donne donc plus d'information que simplement une valeur centrale et une dispersion autour de cette valeur. Dans le cas de l'échantillon de toutes les masses connues des exoplanètes (figure de droite), l'histogramme montre que la répartition des exoplanètes a un pic aux alentours de
, la masse de Jupiter. L'histogramme des masses donne donc plus d'information que simplement une valeur centrale et une dispersion autour de cette valeur. Dans le cas de l'échantillon de toutes les masses connues des exoplanètes (figure de droite), l'histogramme montre que la répartition des exoplanètes a un pic aux alentours de 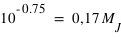 . De plus, le nombre d'exoplanètes avoisinant la masse de la Terre semble très faible. Encore une fois, cette propriété provient très probablement du biais observationnel qui privilégie les planètes massives et ne signifie en aucun cas que les planètes telluriques sont rares.
. De plus, le nombre d'exoplanètes avoisinant la masse de la Terre semble très faible. Encore une fois, cette propriété provient très probablement du biais observationnel qui privilégie les planètes massives et ne signifie en aucun cas que les planètes telluriques sont rares.


 . Elle ne peut donc dépasser 1. Dans notre cas, ce
nombre est le nombre total d'exoplanètes découvertes : 1032. Le grand avantage comparé à l'histogramme est qu'il n'existe qu'une fonction de distribution pour un échantillon, alors qu'il existe un grand nombre d'histogrammes du fait du choix de la taille de l'intervalle. La fonction de distribution est clairement définie et se trouve donc être très appréciée en théorie des probabilités. La fonction de distribution des masses des exoplanètes fournit, entre autres choses, le nombre d'exoplanètes ayant une masse inférieure à 1
. Elle ne peut donc dépasser 1. Dans notre cas, ce
nombre est le nombre total d'exoplanètes découvertes : 1032. Le grand avantage comparé à l'histogramme est qu'il n'existe qu'une fonction de distribution pour un échantillon, alors qu'il existe un grand nombre d'histogrammes du fait du choix de la taille de l'intervalle. La fonction de distribution est clairement définie et se trouve donc être très appréciée en théorie des probabilités. La fonction de distribution des masses des exoplanètes fournit, entre autres choses, le nombre d'exoplanètes ayant une masse inférieure à 1  ,
, 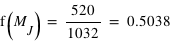 , ou à une masse terrestre,
, ou à une masse terrestre, 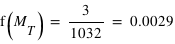 . La figure en bas à droite montre cette fonction.
. La figure en bas à droite montre cette fonction.
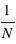 du fait de la normalisation. Entre les deux valeurs, elle est constante. Cette fonction est par construction croissante. Les "créneaux" se distinguent bien pour des échantillons avec un faible nombre d'éléments comme avec les masses des planètes du système solaire mais presque plus lorsque ce nombre est grand pour les exoplanètes (voir figures de droite).
du fait de la normalisation. Entre les deux valeurs, elle est constante. Cette fonction est par construction croissante. Les "créneaux" se distinguent bien pour des échantillons avec un faible nombre d'éléments comme avec les masses des planètes du système solaire mais presque plus lorsque ce nombre est grand pour les exoplanètes (voir figures de droite).
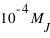 alors que celles des exoplanètes à
alors que celles des exoplanètes à 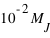 , bien qu'il y ait quelques traces d'exoplanètes en deçà de cette valeur. La pente globale de la fonction de distribution du système solaire semble régulière alors que celle des exoplanètes connaît une augmentation autour de la valeur 0,17
, bien qu'il y ait quelques traces d'exoplanètes en deçà de cette valeur. La pente globale de la fonction de distribution du système solaire semble régulière alors que celle des exoplanètes connaît une augmentation autour de la valeur 0,17 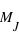 .
.

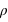 , était constante, ce qui est faux dans notre système solaire, alors le rayon,
, était constante, ce qui est faux dans notre système solaire, alors le rayon, 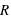 , d'une exoplanète devrait être directement corrélé avec sa masse totale,
, d'une exoplanète devrait être directement corrélé avec sa masse totale, 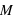 , par la loi
, par la loi 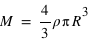 . Un graphique ayant comme abscisse le rayon au cube et comme ordonnée la masse montrerait une droite qui permettrait de calculer
. Un graphique ayant comme abscisse le rayon au cube et comme ordonnée la masse montrerait une droite qui permettrait de calculer 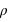 , son coefficient directeur. Dans les faits, la densité des exoplanètes n'est pas constante.
, son coefficient directeur. Dans les faits, la densité des exoplanètes n'est pas constante.


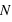 , qui est le signal recherché. L'écart-type, qui est une estimation de son erreur absolue, vaudra alors
, qui est le signal recherché. L'écart-type, qui est une estimation de son erreur absolue, vaudra alors 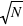 ; ceci est une propriété de la loi de Poisson. Par exemple, si N vaut 10, son erreur absolue vaut
; ceci est une propriété de la loi de Poisson. Par exemple, si N vaut 10, son erreur absolue vaut 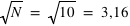 . Le rapport entre le signal, 10, et l'erreur appelé bruit, 3,16, vaut alors
. Le rapport entre le signal, 10, et l'erreur appelé bruit, 3,16, vaut alors
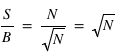
 , donne
, donne 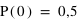 et
et 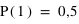 . Cela signifie qu'il y a la même chance de tomber sur pile que sur face. Par contre si la pièce était faussée, il serait possible d'avoir une fonction de probabilité donnant :
. Cela signifie qu'il y a la même chance de tomber sur pile que sur face. Par contre si la pièce était faussée, il serait possible d'avoir une fonction de probabilité donnant : 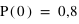 et
et 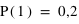 . "pile" aurait alors 4 fois plus de chance de sortir.
. "pile" aurait alors 4 fois plus de chance de sortir.
 de 1 à 6,
de 1 à 6, 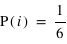 . Il y a en effet autant de chance de tirer un 1, un 2, etc. Cependant quelle est la probabilité de tirer un nombre pair, {2, 4, 6} ? Intuitivement, cette probabilité doit être plus grande que de tirer seulement un 2. Le bon sens et la construction de la théorie des probabilités impliquent qu'elle corresponde à la somme de chacune de leur probabilité. Donc
. Il y a en effet autant de chance de tirer un 1, un 2, etc. Cependant quelle est la probabilité de tirer un nombre pair, {2, 4, 6} ? Intuitivement, cette probabilité doit être plus grande que de tirer seulement un 2. Le bon sens et la construction de la théorie des probabilités impliquent qu'elle corresponde à la somme de chacune de leur probabilité. Donc 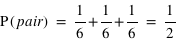 . Il en est de même pour la probabilité de tirer un nombre impair. Ce petit exemple illustre une loi simple de probabilité. La détermination de la probabilité d'un sous-ensemble est égale à la somme de la probabilité de chacun des événements du sous-ensemble.
. Il en est de même pour la probabilité de tirer un nombre impair. Ce petit exemple illustre une loi simple de probabilité. La détermination de la probabilité d'un sous-ensemble est égale à la somme de la probabilité de chacun des événements du sous-ensemble.
 26 = 1/2 car il y a 26 cartes rouges, la moitié du nombre des cartes. La probabilité de tirer une carte noire vaut aussi 1/2, quant à celle de tirer un coeur, elle vaut 1/4 et celle de tirer un roi 1/13. Quelle est alors la probabilité de tirer une carte rouge ou noire ? ou la probabilité de tirer une carte rouge ou de coeur ? ou encore une carte rouge ou un roi ? Pour la première probabilité, intuitivement le résultat est 1 car c'est l'ensemble univers. Cela revient à la somme des probabilités des sous-ensembles : 1/2+1/2. Pour la seconde, la probabilité reste celle de tirer une carte rouge, 1/2, car obligatoirement un coeur est une carte rouge. On n'additionne donc pas les probabilités. Le dernier cas est plus compliqué car deux rois font partie de l'ensemble des cartes rouges mais les deux autres non. Comment faire ? La relation donnant la solution générale est
26 = 1/2 car il y a 26 cartes rouges, la moitié du nombre des cartes. La probabilité de tirer une carte noire vaut aussi 1/2, quant à celle de tirer un coeur, elle vaut 1/4 et celle de tirer un roi 1/13. Quelle est alors la probabilité de tirer une carte rouge ou noire ? ou la probabilité de tirer une carte rouge ou de coeur ? ou encore une carte rouge ou un roi ? Pour la première probabilité, intuitivement le résultat est 1 car c'est l'ensemble univers. Cela revient à la somme des probabilités des sous-ensembles : 1/2+1/2. Pour la seconde, la probabilité reste celle de tirer une carte rouge, 1/2, car obligatoirement un coeur est une carte rouge. On n'additionne donc pas les probabilités. Le dernier cas est plus compliqué car deux rois font partie de l'ensemble des cartes rouges mais les deux autres non. Comment faire ? La relation donnant la solution générale est
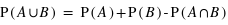
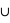 l'union de deux ensembles et
l'union de deux ensembles et  leur intersection. Vous pouvez vérifier que cela donne bien les résultats des deux premiers exemples. Dans le cas des rois, la probabilité est alors P(rouge
leur intersection. Vous pouvez vérifier que cela donne bien les résultats des deux premiers exemples. Dans le cas des rois, la probabilité est alors P(rouge  rois) = P(rouge) + P(rois) - P(rois
rois) = P(rouge) + P(rois) - P(rois  rouge). Il se trouve que l'ensemble {rois
rouge). Il se trouve que l'ensemble {rois  rouge} n'est formé que des deux rois rouges, donc sa probabilité est 2
rouge} n'est formé que des deux rois rouges, donc sa probabilité est 2  1/52 = 1/26. Le résultat est donc P(rois
1/52 = 1/26. Le résultat est donc P(rois  rouge) = 1/2 + 1/13 - 1/26 = 1/2 + 1/26 = 14/26.
rouge) = 1/2 + 1/13 - 1/26 = 1/2 + 1/26 = 14/26.
 B} = {}, donc si A et B sont disjoints, il suffit alors de sommer la probabilité de A et de B pour avoir celle de A
B} = {}, donc si A et B sont disjoints, il suffit alors de sommer la probabilité de A et de B pour avoir celle de A B car P({}) = 0.
B car P({}) = 0.
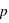 . Cela est vrai pour un jet de dé ou de pièce non faussés, ou pour un jeu de cartes bien mélangé. Dans ce cas, la probabilité de tous les évènements, donc de l'ensemble univers, vaut P({E1, E2, E3, ..., En}) = P({E1}) + P({E2})+ P({E3})+ ... + P({En}) = p +p +p +...+p =
. Cela est vrai pour un jet de dé ou de pièce non faussés, ou pour un jeu de cartes bien mélangé. Dans ce cas, la probabilité de tous les évènements, donc de l'ensemble univers, vaut P({E1, E2, E3, ..., En}) = P({E1}) + P({E2})+ P({E3})+ ... + P({En}) = p +p +p +...+p = 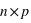 car tous les ensembles d'évènements sont disjoints, c'est à dire pour tous
car tous les ensembles d'évènements sont disjoints, c'est à dire pour tous 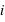 et
et 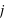 , {
, {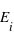
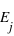 } = {}. Or la probabilité de l'ensemble univers vaut par définition 1. Donc
} = {}. Or la probabilité de l'ensemble univers vaut par définition 1. Donc 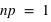 ce qui implique que
ce qui implique que 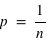 . Cela justifie pourquoi la probabilité pour le lancer d'une pièce vaut 1/2, pour le jet d'un dé vaut 1/6 et pour le tirage d'une carte dans un jeu de 52 cartes vaut 1/52.
. Cela justifie pourquoi la probabilité pour le lancer d'une pièce vaut 1/2, pour le jet d'un dé vaut 1/6 et pour le tirage d'une carte dans un jeu de 52 cartes vaut 1/52.

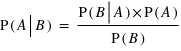
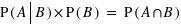 et que, de même,
et que, de même, 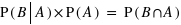 donc que
donc que 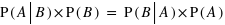 .
.
 P(Blanche|Urne A)+P(Urne B)
P(Blanche|Urne A)+P(Urne B) P(Blanche|Urne B) = 0,5
P(Blanche|Urne B) = 0,5 9/10 + 0,5
9/10 + 0,5 1/10 = 0,5 car il est possible de tirer une boule blanche depuis l'urne A ou depuis l'urne B, mais pas avec la même probabilité. Ainsi, la probabilité que l'on soit en présence de l'urne A sachant que l'on a tiré une boule blanche est donnée par P(Urne A|Blanche) = P(Blanche|Urne A)
1/10 = 0,5 car il est possible de tirer une boule blanche depuis l'urne A ou depuis l'urne B, mais pas avec la même probabilité. Ainsi, la probabilité que l'on soit en présence de l'urne A sachant que l'on a tiré une boule blanche est donnée par P(Urne A|Blanche) = P(Blanche|Urne A) P(Urne A)/P(Blanche) = 9/10
P(Urne A)/P(Blanche) = 9/10 0,5/0,5 = 9/10. Dans l'autre cas P(Blanche|Urne B) = 1/10. Avec cette observation du tirage d'une boule blanche, on est passé d'une probabilité de 0,5 pour que l'urne étudiée soit l'urne A, à une probabilité de 9/10 pour que l'urne étudiée soit l'urne A.
0,5/0,5 = 9/10. Dans l'autre cas P(Blanche|Urne B) = 1/10. Avec cette observation du tirage d'une boule blanche, on est passé d'une probabilité de 0,5 pour que l'urne étudiée soit l'urne A, à une probabilité de 9/10 pour que l'urne étudiée soit l'urne A.
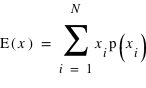 . De manière similaire, elle se définit pour une variable continue
. De manière similaire, elle se définit pour une variable continue 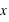 :
: 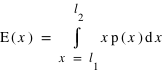 où
où 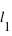 et
et 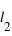 sont les limites inférieures et supérieures que peut prendre la variable
sont les limites inférieures et supérieures que peut prendre la variable 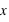 .
.
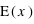 = 1
= 1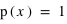 ), l'espérance est
), l'espérance est 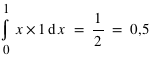 . Moyenne et espérance se ressemblent beaucoup, cependant elle ont une différence. L'espérance est une valeur dans le cadre de la théorie des probabilités associée à une loi de probabilité. La moyenne est, quant à elle, le résultat d'une opération arithmétique sur un échantillon. La moyenne dépend donc de l'échantillon alors que l'espérance est théorique et donc unique pour une loi donnée. La moyenne calculée à partir d'un échantillon doit être proche de l'espérance mais pas forcément identique. Par exemple, lorsqu'un dé est tiré 10 fois et que la moyenne des résultats est faite, le résultat n'est pas forcément l'espérance de 3,5. De plus, si l'on refait 10 lancers la nouvelle moyenne ne sera pas forcément identique à la première. Cependant, d'après la loi des grands nombres, plus le nombre de lancers de dé sera grand, plus la moyenne s'approchera de l'espérance. L'espérance doit être vue comme la limite de la moyenne lorsque l'on fait tendre le nombre d'essais vers l'infini.
. Moyenne et espérance se ressemblent beaucoup, cependant elle ont une différence. L'espérance est une valeur dans le cadre de la théorie des probabilités associée à une loi de probabilité. La moyenne est, quant à elle, le résultat d'une opération arithmétique sur un échantillon. La moyenne dépend donc de l'échantillon alors que l'espérance est théorique et donc unique pour une loi donnée. La moyenne calculée à partir d'un échantillon doit être proche de l'espérance mais pas forcément identique. Par exemple, lorsqu'un dé est tiré 10 fois et que la moyenne des résultats est faite, le résultat n'est pas forcément l'espérance de 3,5. De plus, si l'on refait 10 lancers la nouvelle moyenne ne sera pas forcément identique à la première. Cependant, d'après la loi des grands nombres, plus le nombre de lancers de dé sera grand, plus la moyenne s'approchera de l'espérance. L'espérance doit être vue comme la limite de la moyenne lorsque l'on fait tendre le nombre d'essais vers l'infini.
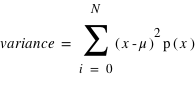 avec
avec  l'espérance. Dans le cas d'une variable continue,
l'espérance. Dans le cas d'une variable continue, 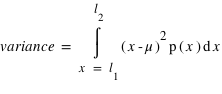 . On peut aussi définir la variance en n'utilisant que l'espérance de la variable
. On peut aussi définir la variance en n'utilisant que l'espérance de la variable  et
et 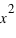 :
: 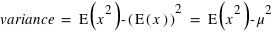 . La démonstration est demandée en exercice. L'écart-type, souvent noté
. La démonstration est demandée en exercice. L'écart-type, souvent noté 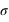 , est la racine carrée de la variance :
, est la racine carrée de la variance : 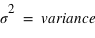 . De même que pour le couple espérance-moyenne, le terme variance s'utilise plutôt en probabilité et écart-type en statistique.
. De même que pour le couple espérance-moyenne, le terme variance s'utilise plutôt en probabilité et écart-type en statistique.

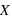 , la fonction de distribution, notée
, la fonction de distribution, notée 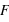 , donne la probabilité d'avoir la variable
, donne la probabilité d'avoir la variable 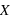 strictement plus petite que
strictement plus petite que 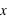 :
: 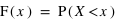 . La fonction
. La fonction  est donc par définition une fonction croissante et bornée par la valeur 1. Cette définition convient aussi bien aux variables discrètes qu'aux variables continues. Il est aisé avec cette fonction de calculer la probabilité d'avoir la variable
est donc par définition une fonction croissante et bornée par la valeur 1. Cette définition convient aussi bien aux variables discrètes qu'aux variables continues. Il est aisé avec cette fonction de calculer la probabilité d'avoir la variable  entre
entre  et
et 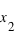 . C'est tout simplement
. C'est tout simplement 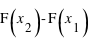 . En conséquence, si la courbe est plate ou avec une pente faible entre deux points
. En conséquence, si la courbe est plate ou avec une pente faible entre deux points  et
et  , cela conduit à une probabilité entre
, cela conduit à une probabilité entre 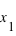 et
et 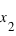 faible alors que si la pente est forte la probabilité l'est aussi.
faible alors que si la pente est forte la probabilité l'est aussi.
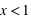 , la fonction est nulle, il est en effet impossible qu'un jet de dé puisse sortir un nombre plus petit que 1. De
, la fonction est nulle, il est en effet impossible qu'un jet de dé puisse sortir un nombre plus petit que 1. De 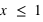 à
à 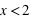 ,
,  est constante et vaut 1/6 qui est la probabilité d'avoir un 1 à un jet de dé. Ensuite entre 2 et 3 exclus, la fonction vaut
est constante et vaut 1/6 qui est la probabilité d'avoir un 1 à un jet de dé. Ensuite entre 2 et 3 exclus, la fonction vaut 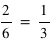 ; cela correspond à la probabilité de sortir un 1 ou un 2. La fonction continue d'augmenter pour plafonner jusqu'à x>6 où elle atteint sa valeur maximale de 1 car il est certain qu'un dé sorte un chiffre plus petit ou égale à 6.
; cela correspond à la probabilité de sortir un 1 ou un 2. La fonction continue d'augmenter pour plafonner jusqu'à x>6 où elle atteint sa valeur maximale de 1 car il est certain qu'un dé sorte un chiffre plus petit ou égale à 6.
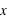 ,
, 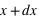 ] est identique. Cette fonction de distribution n'est autre que la fonction de distribution de la loi uniforme entre 0 et 1 ; chaque nombre entre 0 et 1 ayant la même chance d'être tiré.
] est identique. Cette fonction de distribution n'est autre que la fonction de distribution de la loi uniforme entre 0 et 1 ; chaque nombre entre 0 et 1 ayant la même chance d'être tiré.

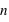 ) d'une loi à deux évènements et pour différentes probabilités de l'évènement 0 (
) d'une loi à deux évènements et pour différentes probabilités de l'évènement 0 (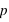 ). Pour le même nombre de lancers
). Pour le même nombre de lancers 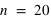 , le pic est à 14 avec un probabilté
, le pic est à 14 avec un probabilté 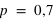 et seulement 10 avec
et seulement 10 avec 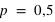 . Pour
. Pour 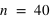 et
et 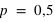 , le pic est à 20, à la moitié du nombre de lancers, car il y autant de chance d'avoir l'évènement 0 que 1. En comparaison de
, le pic est à 20, à la moitié du nombre de lancers, car il y autant de chance d'avoir l'évènement 0 que 1. En comparaison de 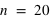 et
et 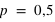 , lorsque
, lorsque 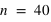 , la fonction a un pic moins haut mais plus reséré, cela est dû au fait que le rapport entre l'espérance et l'écart type tend vers 0 lorsque
, la fonction a un pic moins haut mais plus reséré, cela est dû au fait que le rapport entre l'espérance et l'écart type tend vers 0 lorsque  tend vers l'infini.
tend vers l'infini.
 alors que l'événement 1 a une probabilité notée
alors que l'événement 1 a une probabilité notée 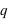 . Toujours, dans le cas d'une pièce de monnaie,
. Toujours, dans le cas d'une pièce de monnaie, 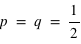 . De manière générale,
. De manière générale,  et
et  n'ont aucune raison d'être identiques comme dans le cas de la pièce de monnaie. Je peux inventer une expérience où je définis l'évènement 0 si un dé sort la valeur 1 et l'événement 1 si un dé sort 2, 3, 4, 5 ou 6. Dans ce cas
n'ont aucune raison d'être identiques comme dans le cas de la pièce de monnaie. Je peux inventer une expérience où je définis l'évènement 0 si un dé sort la valeur 1 et l'événement 1 si un dé sort 2, 3, 4, 5 ou 6. Dans ce cas 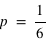 et
et 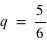 . De manière générale comme 0 et 1 forment l'ensemble univers, alors la probabilité
. De manière générale comme 0 et 1 forment l'ensemble univers, alors la probabilité 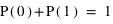 donc
donc 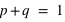 et
et 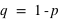 . Les lois à deux événements ne dépendent donc que d'un paramètre,
. Les lois à deux événements ne dépendent donc que d'un paramètre,  .
.
 de la loi à deux événements et le nombre de répétition de cette loi,
de la loi à deux événements et le nombre de répétition de cette loi,  . Son ensemble univers est constitué de toutes les séries possibles de
. Son ensemble univers est constitué de toutes les séries possibles de 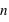 répétitions de la loi à deux évènements. Le nombre d'événements vaut donc
répétitions de la loi à deux évènements. Le nombre d'événements vaut donc 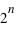 car à chaque répétition (
car à chaque répétition (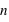 en tout) il y a deux événements possibles. Par exemple, lancer une pièce trois fois donne
en tout) il y a deux événements possibles. Par exemple, lancer une pièce trois fois donne 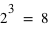 évènements possibles. L'ensemble univers est en ce cas : (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Chaque évènement est donc constitué d'un certain nombre de 0, noté
évènements possibles. L'ensemble univers est en ce cas : (0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1). Chaque évènement est donc constitué d'un certain nombre de 0, noté 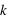 , et de 1, noté
, et de 1, noté 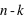 . Par définition la probabilité de 0 vaut
. Par définition la probabilité de 0 vaut 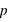 et celle de 1 vaut
et celle de 1 vaut 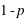 . Donc la probabilité d'un évènement est
. Donc la probabilité d'un évènement est 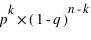 . L'intérêt dans ce type d'expérience est de savoir combien de fois sort l'évènement 0 ou 1 mais sans se soucier de l'ordre. Les évènements (0, 1, 0) ou (1, 0, 0) sont alors considérés comme identiques. La loi binomiale fournit la probabilité de tirer
. L'intérêt dans ce type d'expérience est de savoir combien de fois sort l'évènement 0 ou 1 mais sans se soucier de l'ordre. Les évènements (0, 1, 0) ou (1, 0, 0) sont alors considérés comme identiques. La loi binomiale fournit la probabilité de tirer  évènements 0 sur
évènements 0 sur  lancers. Pour cela, il suffit de remarquer que pour un nombre
lancers. Pour cela, il suffit de remarquer que pour un nombre  d'événements 0 parmi
d'événements 0 parmi  lancers, il est possible d'effectuer
lancers, il est possible d'effectuer 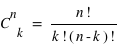 permutations. Donc la probabilité recherchée, notée
permutations. Donc la probabilité recherchée, notée  , vaut
, vaut 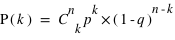 .
.
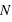 lancers, plus un évènement aura une grande probabilité plus il sortira souvent. Cependant, il est rare qu'il sorte pour chaque lancer. En conséquence, le pic de probabilité de la loi binomiale se situe en
lancers, plus un évènement aura une grande probabilité plus il sortira souvent. Cependant, il est rare qu'il sorte pour chaque lancer. En conséquence, le pic de probabilité de la loi binomiale se situe en ![E[(N+1)*p]](../pages_stat-theorie/equations_stat-theorie/equation118.png) , où
, où 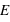 est la partie entière. Si p tend vers 1 alors le pic tendra vers
est la partie entière. Si p tend vers 1 alors le pic tendra vers 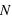 , à l'inverse il tendra vers 0. De plus, l'espérance de la loi binomiale vaut
, à l'inverse il tendra vers 0. De plus, l'espérance de la loi binomiale vaut 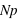 et son écart type vaut
et son écart type vaut 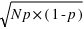 . Dans le cas ou
. Dans le cas ou  est très grand, un million par exemple, Le rapport écart-type sur espérance vaut
est très grand, un million par exemple, Le rapport écart-type sur espérance vaut 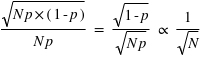 , il tend vers zéro. Si l'on voit l'espérance comme la mesure d'une observation et l'écart type comme son incertitude absolue alors, si
, il tend vers zéro. Si l'on voit l'espérance comme la mesure d'une observation et l'écart type comme son incertitude absolue alors, si 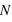 est très grand, l'incertitude relative sur la mesure sera très faible. Par exemple, dans un métal constitué de milliards d'atomes, supposons que les spins de chaque atome puissent être en haut ou en bas avec la même probabilité,
est très grand, l'incertitude relative sur la mesure sera très faible. Par exemple, dans un métal constitué de milliards d'atomes, supposons que les spins de chaque atome puissent être en haut ou en bas avec la même probabilité, 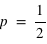 . Alors le métal n'aura pas de champ magnétique significatif car il aura statistiquement à chaque instant quasiment autant de spins en haut qu'en bas. La différence instantanée entre le nombre d'atomes ayant un spin en haut ou en bas, générateur d'un champ magnétique, sera en ordre de grandeur
. Alors le métal n'aura pas de champ magnétique significatif car il aura statistiquement à chaque instant quasiment autant de spins en haut qu'en bas. La différence instantanée entre le nombre d'atomes ayant un spin en haut ou en bas, générateur d'un champ magnétique, sera en ordre de grandeur 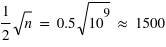 ; ce qui fournira des champs très faibles en comparaison du potentiel que pourraient produire les
; ce qui fournira des champs très faibles en comparaison du potentiel que pourraient produire les 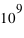 atomes du métal si tous les spins étaient alignés dans le même sens. De plus, ce champ magnétique est très instable dans le temps (on dit qu'il fluctue) et a une moyenne nulle au cours du temps.
atomes du métal si tous les spins étaient alignés dans le même sens. De plus, ce champ magnétique est très instable dans le temps (on dit qu'il fluctue) et a une moyenne nulle au cours du temps.

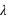 : 1, 4 et 10.
: 1, 4 et 10.
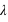 . La loi de probabilité de la loi de Poisson est
. La loi de probabilité de la loi de Poisson est  toujours positive (voir figure). Si
toujours positive (voir figure). Si 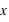 vaut 0, comme
vaut 0, comme 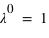 et
et 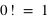 , alors
, alors 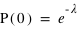 . Lorsque
. Lorsque  tend vers l'infini,
tend vers l'infini, 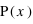 tend vers 0 du fait du terme en factorielle qui domine le terme
tend vers 0 du fait du terme en factorielle qui domine le terme 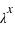 . Cette loi de probabilité admet un unique pic, appelé aussi mode, avec la valeur de
. Cette loi de probabilité admet un unique pic, appelé aussi mode, avec la valeur de 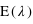 , si
, si 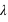 n'est pas un entier, et deux pics,
n'est pas un entier, et deux pics, 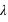 et
et 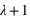 , si
, si 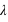 est un entier. L'espérance ainsi que la variance de cette fonction valent
est un entier. L'espérance ainsi que la variance de cette fonction valent 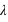 . L'écart type vaut donc
. L'écart type vaut donc 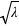 .
.
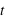 par un pixel de caméra CCD suivent une loi de Poisson. De ce fait, lorsque plusieurs poses du même objet astronomique sont faites, durant par exemple 10 minutes, le nombre de photons d'un pixel provenant de l'objet décrit une loi de Poisson dont la moyenne qui est la mesure physique est le paramètre de la loi.
par un pixel de caméra CCD suivent une loi de Poisson. De ce fait, lorsque plusieurs poses du même objet astronomique sont faites, durant par exemple 10 minutes, le nombre de photons d'un pixel provenant de l'objet décrit une loi de Poisson dont la moyenne qui est la mesure physique est le paramètre de la loi.



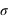 des différents quartiles. Figure du bas, la probabilité d'avoir un résultat entre [
des différents quartiles. Figure du bas, la probabilité d'avoir un résultat entre [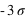 ,
, 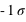 ] (15,73 %), entre [
] (15,73 %), entre [ ,
,  ] (68,27 %) et enfin entre [
] (68,27 %) et enfin entre [ ,
,  ] (15,73 %).
] (15,73 %).
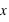 ,
, 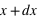 ], cette loi de probabilité vaut :
], cette loi de probabilité vaut : 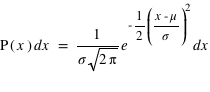 . Elle a deux paramètres qui sont
. Elle a deux paramètres qui sont 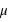 , l'espérance de la fonction de probabilité, et
, l'espérance de la fonction de probabilité, et 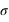 , l'écart type. Le terme devant l'exponentielle est un terme de normalisation afin que la probabilité totale de l'univers, donné par l'intégrale de cette loi depuis
, l'écart type. Le terme devant l'exponentielle est un terme de normalisation afin que la probabilité totale de l'univers, donné par l'intégrale de cette loi depuis  jusque
jusque  , vale 1. Le mode, valeur pour laquelle la fonction connaît un pic, est égale à sa moyenne,
, vale 1. Le mode, valeur pour laquelle la fonction connaît un pic, est égale à sa moyenne, 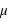 . L'écart-type à l'espérance est donné par
. L'écart-type à l'espérance est donné par 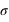 . A
. A 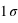 la probabilité chute d'une facteur
la probabilité chute d'une facteur 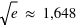 ; à
; à 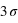 , ce facteur devient
, ce facteur devient 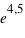 , soit un peu plus de 90. La chute est donc très rapide à mesure qu'on s'éloigne de la valeur moyenne. En d'autres termes, la probabilité de voir sortir un réel séparé de plus de
, soit un peu plus de 90. La chute est donc très rapide à mesure qu'on s'éloigne de la valeur moyenne. En d'autres termes, la probabilité de voir sortir un réel séparé de plus de 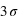 de la moyenne devient très faible, et cette probabilité devient quasiment nulle à
de la moyenne devient très faible, et cette probabilité devient quasiment nulle à 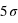 (voir la troisième figure).
(voir la troisième figure).
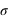 . Si la moyenne diffère significativement de l'espérance ("signifcativement" voulant dire "par rapport à l'écart-type"), on parle de mesure biaisée.
. Si la moyenne diffère significativement de l'espérance ("signifcativement" voulant dire "par rapport à l'écart-type"), on parle de mesure biaisée.
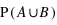 , le signe
, le signe 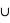 signifiant Union ?
signifiant Union ?
 par rapport à
par rapport à  et
et 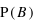 pour des variables discrètes à valeurs dans un ensemble fini ? Donner un exemple où
pour des variables discrètes à valeurs dans un ensemble fini ? Donner un exemple où 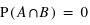 . Notez que le symbole
. Notez que le symbole  signifie l'intersection.
signifie l'intersection.
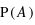 ?
?
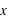 , Démontrer que
, Démontrer que 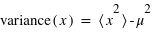 pour une variable discrète. (La démonstration est similaire pour une variable continue en changeant le signe somme en intégrale).
pour une variable discrète. (La démonstration est similaire pour une variable continue en changeant le signe somme en intégrale). 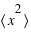 signifie l'espérance de
signifie l'espérance de 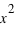 et
et 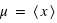 .
.
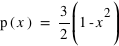 pour x dans l'intervall [0, 1], et
pour x dans l'intervall [0, 1], et 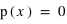 en dehors.
en dehors.
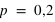 , quelles sont alors les probabilités d'avoir 28 faces ou 13 piles ?
, quelles sont alors les probabilités d'avoir 28 faces ou 13 piles ?
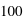 m², il tombe des gouttes de pluie en 10 secondes suivant une loi de Poisson de paramètre
m², il tombe des gouttes de pluie en 10 secondes suivant une loi de Poisson de paramètre 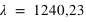 . Combien en moyenne, tombera-t-il de gouttes d'eau dans ce champ en 1 heure ?
. Combien en moyenne, tombera-t-il de gouttes d'eau dans ce champ en 1 heure ?
 (
( étant l'écart-type) ?
étant l'écart-type) ?
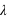 égal à 5.
égal à 5.

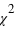 . Ce ne sont ici que des exemples très connus mais le couple probabilité-statistique est bien plus riche et peut servir dans bons nombres de domaines scientifiques et même économiques.
. Ce ne sont ici que des exemples très connus mais le couple probabilité-statistique est bien plus riche et peut servir dans bons nombres de domaines scientifiques et même économiques.
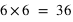 . Une façon plus détaillée de le comprendre est de dire qu'un évènement est le couple des résultats du dé rouge et du dé bleu (Rouge, Bleu). Les couples sont donc (1, 1), (1, 2), (1, 3), (1, 4), ... On retrouve qu'il y a 6 possibilités pour le premier membre du couple et 6 pour l'autre, cela donne 36 possibilités.
. Une façon plus détaillée de le comprendre est de dire qu'un évènement est le couple des résultats du dé rouge et du dé bleu (Rouge, Bleu). Les couples sont donc (1, 1), (1, 2), (1, 3), (1, 4), ... On retrouve qu'il y a 6 possibilités pour le premier membre du couple et 6 pour l'autre, cela donne 36 possibilités.
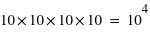 évènements. Le premier est 0,0000 puis 0,0001 etc. et le dernier est 0,9999.
évènements. Le premier est 0,0000 puis 0,0001 etc. et le dernier est 0,9999.
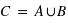 ) se définit comme l'ensemble contenant les éléments se trouvant dans A ou dans B. On a alors
) se définit comme l'ensemble contenant les éléments se trouvant dans A ou dans B. On a alors 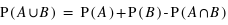 où le symbole
où le symbole  désigne l'intersection.
désigne l'intersection.
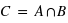 se définit comme l'ensemble contenant les éléments se trouvant dans A etdans B. L'ensemble
se définit comme l'ensemble contenant les éléments se trouvant dans A etdans B. L'ensemble 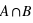 étant par conséquent inlcus dans A et B, sa probabilité sera inférieure ou égale à la probabilité de chacun de ces deux ensembles :
étant par conséquent inlcus dans A et B, sa probabilité sera inférieure ou égale à la probabilité de chacun de ces deux ensembles : 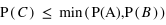 . Dans un jeu de 52 cartes, si A est l'ensemble des cartes rouges et B l'ensemble des cartes noires alors
. Dans un jeu de 52 cartes, si A est l'ensemble des cartes rouges et B l'ensemble des cartes noires alors 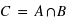 est l'ensemble vide, d'où
est l'ensemble vide, d'où 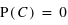 .
.
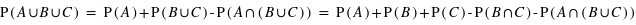 Or
Or 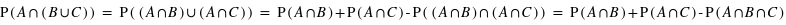 Donc
Donc 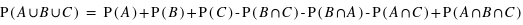
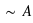 , se définit comme tout ce qui n'est pas coeur : pique, trèfle et carreau. Il est parfois plus simple de définir un ensemble par ce qu'il n'est pas plutôt que par ce qu'il est. De là, le principe du tiers exclu donne
, se définit comme tout ce qui n'est pas coeur : pique, trèfle et carreau. Il est parfois plus simple de définir un ensemble par ce qu'il n'est pas plutôt que par ce qu'il est. De là, le principe du tiers exclu donne 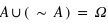 , l'univers des possibles. Or
, l'univers des possibles. Or 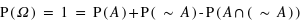 . Comme cette dernière intersection est vide, on a
. Comme cette dernière intersection est vide, on a 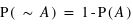 .
.
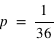
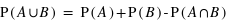 , il est alors possible de calculer la probabilité pour chaque valeur possible de la somme (de 2 à 12). Comme les évènements sont par nature disjoints l'un de l'autre,
, il est alors possible de calculer la probabilité pour chaque valeur possible de la somme (de 2 à 12). Comme les évènements sont par nature disjoints l'un de l'autre, 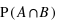 est toujours nulle. De ce fait, pour avoir la probabilité, il suffit de prendre le nombre total de combinaisons donnant la même valeur pour la somme, et de diviser ce nombre par 36.
est toujours nulle. De ce fait, pour avoir la probabilité, il suffit de prendre le nombre total de combinaisons donnant la même valeur pour la somme, et de diviser ce nombre par 36.
 compris entre 2 et 12,
compris entre 2 et 12, 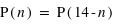 .
.
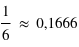 , et celle de faire une somme valant 6 avec deux dés est
, et celle de faire une somme valant 6 avec deux dés est 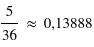 , comme vu à la question précédente. Donc il vaut mieux prendre un seul dé pour espèrer faire un 6.
, comme vu à la question précédente. Donc il vaut mieux prendre un seul dé pour espèrer faire un 6.
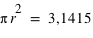 cm2 et celle de la cible tout entière vaut
cm2 et celle de la cible tout entière vaut 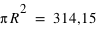 cm2. Or, la probabilité est proportionnelle à la surface, donc la probabilité de toucher la zone centrale, sachant que l'on a touché la cible, est P(toucher la cible)
cm2. Or, la probabilité est proportionnelle à la surface, donc la probabilité de toucher la zone centrale, sachant que l'on a touché la cible, est P(toucher la cible) 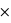 P(toucher la zone centrale | toucher la cible)
P(toucher la zone centrale | toucher la cible)  .
.
 P(non malade) / P(positif). La probabilité d'être non malade est P(non malade) = 0,999 d'après l'énoncé. La probabilité d'être positif mais en étant non malade est P(positif | non malade) = 5% = 0,05, toujours d'après l'énoncé. Il reste le plus difficile, la probabilité d'être dépisté positif, qui est la somme entre les cas (disjoints) "malades" et "non malades" : P(positif) = P(positif | malade)
P(non malade) / P(positif). La probabilité d'être non malade est P(non malade) = 0,999 d'après l'énoncé. La probabilité d'être positif mais en étant non malade est P(positif | non malade) = 5% = 0,05, toujours d'après l'énoncé. Il reste le plus difficile, la probabilité d'être dépisté positif, qui est la somme entre les cas (disjoints) "malades" et "non malades" : P(positif) = P(positif | malade)  P(malade) + P(positif | non malade)
P(malade) + P(positif | non malade)  P(non malade) = 0,99
P(non malade) = 0,99 0,001 + 0,05
0,001 + 0,05 0,999 = 0,00099 + 0,04995 = 0,05094. En définitif, la probabilité d'être faux-positif est P(non malade | positif) = 0,05
0,999 = 0,00099 + 0,04995 = 0,05094. En définitif, la probabilité d'être faux-positif est P(non malade | positif) = 0,05  0,999 / 0,05094
0,999 / 0,05094 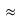 0,98. Donc 98% des patients étant déclarés malades sont en réalité sains.
0,98. Donc 98% des patients étant déclarés malades sont en réalité sains.
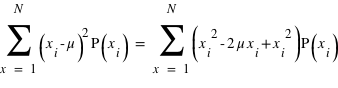 =
= 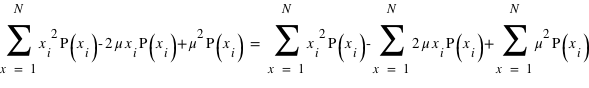 =
= 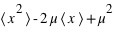 .
Or
.
Or 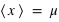 , alors
, alors 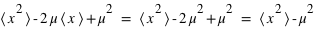 .
Ce qui montre que variance =
.
Ce qui montre que variance = 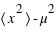 .
.
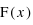 d'une variable aléatoire :
d'une variable aléatoire : 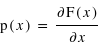 . Cette fonction de distribution décrit la répartition de la variable aléatoire
. Cette fonction de distribution décrit la répartition de la variable aléatoire  selon l'égalité
selon l'égalité 
 et 1 pour
et 1 pour 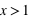 .
La fonction de distribution est l'intégrale de la loi de probabilité. Donc elle vaut
.
La fonction de distribution est l'intégrale de la loi de probabilité. Donc elle vaut 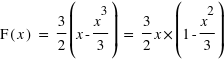 où
où  est la constante de normalisation pour que
est la constante de normalisation pour que 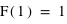 .
.
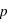 , on a
, on a 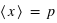 et l'écart-type de
et l'écart-type de 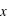 vaut
vaut 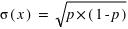
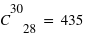 combinaisons pour avoir 28 faces. Il y a
combinaisons pour avoir 28 faces. Il y a 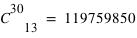 pour avoir 13 piles.
pour avoir 13 piles.
 (face) = 0,8,
(face) = 0,8,  (nombre de "face" = 28) =
(nombre de "face" = 28) = 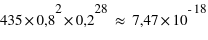 et
et  (nombre de "pile" = 13) =
(nombre de "pile" = 13) = 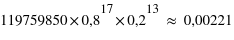
 ,
, 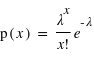 ,
, 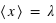 et
et 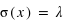
 gouttes. Comme en une heure, il y a 360 fois 10 secondes, donc en 1 heure, il tombe en moyenne 446482,8 gouttes.
gouttes. Comme en une heure, il y a 360 fois 10 secondes, donc en 1 heure, il tombe en moyenne 446482,8 gouttes.
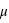 et d'écart-type
et d'écart-type 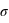 , on a
, on a 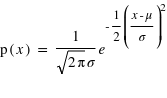
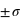 est donnée avec la loi de distribution :
est donnée avec la loi de distribution : 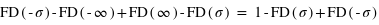 .
En regardant le cours, on calcule que la probabilité est d'environ 0,3173 en dehors de
.
En regardant le cours, on calcule que la probabilité est d'environ 0,3173 en dehors de 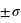 et d'environ 0,0027 en dehors de
et d'environ 0,0027 en dehors de 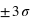 .
.
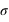 de la valeure théorique. Cela est probable (31,73% de chance, voir question ci-dessus) ; la théorie ne semble pas fausse. Par contre si l'écart-type attendu est 0,05 alors la mesure est à 10
de la valeure théorique. Cela est probable (31,73% de chance, voir question ci-dessus) ; la théorie ne semble pas fausse. Par contre si l'écart-type attendu est 0,05 alors la mesure est à 10  . A trois
. A trois  , la probabilité est déjà faible (0,0027) mais à 10
, la probabilité est déjà faible (0,0027) mais à 10  elle est infinitésimale. La théorie semble alors invalidée par l'expérience.
elle est infinitésimale. La théorie semble alors invalidée par l'expérience.