Temps
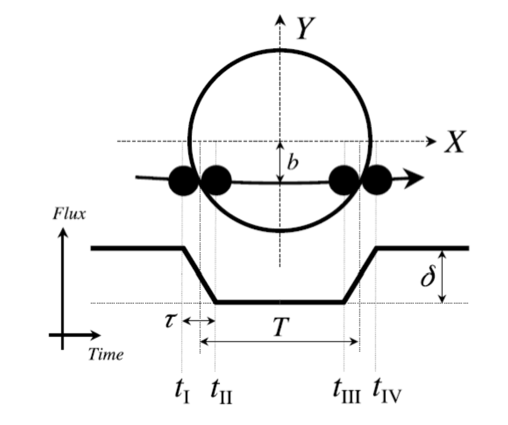
Figure 5 : Géométrie d’un transit. δ est la profondeur du transit, b le paramètre d’impact, T la durée du transit et τ la durée de l’ingress.
Crédit :
à traduire
La géométrie d’un transit est représentée sur la Fig. 5.
Appelons 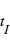 à
à 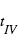 les 4 « temps de contact », c’est-à-dire les instants auxquels les disques de la planète et de l’étoile sont tangents. L’instant moyen de l’entrée (du disque planétaire devant le disque stellaire) est
les 4 « temps de contact », c’est-à-dire les instants auxquels les disques de la planète et de l’étoile sont tangents. L’instant moyen de l’entrée (du disque planétaire devant le disque stellaire) est 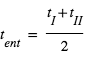 ; de même l’instant moyen de la sortie (du disque planétaire) est
; de même l’instant moyen de la sortie (du disque planétaire) est 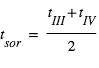 . L’intervalle de temps séparant ces deux instants, noté T, est par définition la « durée du transit », alors que
. L’intervalle de temps séparant ces deux instants, noté T, est par définition la « durée du transit », alors que 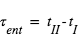 et
et 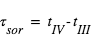 sont respectivement la durée de l’entrée et de la sortie. On note également b le « paramètre d’impact », i.e. la distance minimale – exprimée en fraction de rayon stellaire – entre la position apparente de la planète et le centre de l’étoile.
sont respectivement la durée de l’entrée et de la sortie. On note également b le « paramètre d’impact », i.e. la distance minimale – exprimée en fraction de rayon stellaire – entre la position apparente de la planète et le centre de l’étoile.
Avec ces définitions, en se limitant au cas des orbites circulaires et en faisant les approximations raisonnables suivantes : 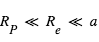 , et
, et 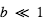 (transit non-rasant), on peut montrer que la durée du transit est égale à :
(transit non-rasant), on peut montrer que la durée du transit est égale à :
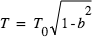 où
où 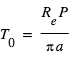 , P étant la période orbitale.
, P étant la période orbitale.
Par ailleurs, 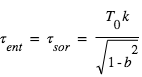 , où
, où 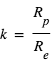 En combinant l’expression de
En combinant l’expression de 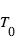 ci-dessus avec la 3eme loi de Kepler, et en se ramenant au cas du système solaire, on obtient
ci-dessus avec la 3eme loi de Kepler, et en se ramenant au cas du système solaire, on obtient 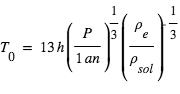 expression dans laquelle la seconde parenthèse représente le rapport de la densité de l’étoile à celle du Soleil. Ainsi, vu depuis une autre étoile, le transit de la Terre devant le Soleil ne dure que 13 h une fois tous les ans, et celui de Jupiter ne dure que 30 h une fois tous les douze ans, ce qui illustre à nouveau la rareté du phénomène. Bien évidemment, la mesure de la période requiert l’observation d’au moins deux transits.
expression dans laquelle la seconde parenthèse représente le rapport de la densité de l’étoile à celle du Soleil. Ainsi, vu depuis une autre étoile, le transit de la Terre devant le Soleil ne dure que 13 h une fois tous les ans, et celui de Jupiter ne dure que 30 h une fois tous les douze ans, ce qui illustre à nouveau la rareté du phénomène. Bien évidemment, la mesure de la période requiert l’observation d’au moins deux transits.

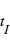 à
à 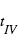 les 4 « temps de contact », c’est-à-dire les instants auxquels les disques de la planète et de l’étoile sont tangents. L’instant moyen de l’entrée (du disque planétaire devant le disque stellaire) est
les 4 « temps de contact », c’est-à-dire les instants auxquels les disques de la planète et de l’étoile sont tangents. L’instant moyen de l’entrée (du disque planétaire devant le disque stellaire) est 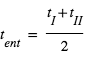 ; de même l’instant moyen de la sortie (du disque planétaire) est
; de même l’instant moyen de la sortie (du disque planétaire) est 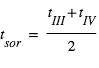 . L’intervalle de temps séparant ces deux instants, noté T, est par définition la « durée du transit », alors que
. L’intervalle de temps séparant ces deux instants, noté T, est par définition la « durée du transit », alors que 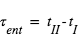 et
et 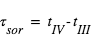 sont respectivement la durée de l’entrée et de la sortie. On note également b le « paramètre d’impact », i.e. la distance minimale – exprimée en fraction de rayon stellaire – entre la position apparente de la planète et le centre de l’étoile.
sont respectivement la durée de l’entrée et de la sortie. On note également b le « paramètre d’impact », i.e. la distance minimale – exprimée en fraction de rayon stellaire – entre la position apparente de la planète et le centre de l’étoile.
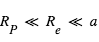 , et
, et 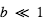 (transit non-rasant), on peut montrer que la durée du transit est égale à :
(transit non-rasant), on peut montrer que la durée du transit est égale à :
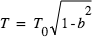 où
où 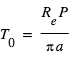 , P étant la période orbitale.
, P étant la période orbitale.
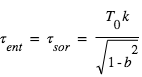 , où
, où 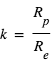 En combinant l’expression de
En combinant l’expression de 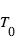 ci-dessus avec la 3eme loi de Kepler, et en se ramenant au cas du système solaire, on obtient
ci-dessus avec la 3eme loi de Kepler, et en se ramenant au cas du système solaire, on obtient 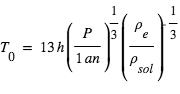 expression dans laquelle la seconde parenthèse représente le rapport de la densité de l’étoile à celle du Soleil. Ainsi, vu depuis une autre étoile, le transit de la Terre devant le Soleil ne dure que 13 h une fois tous les ans, et celui de Jupiter ne dure que 30 h une fois tous les douze ans, ce qui illustre à nouveau la rareté du phénomène. Bien évidemment, la mesure de la période requiert l’observation d’au moins deux transits.
expression dans laquelle la seconde parenthèse représente le rapport de la densité de l’étoile à celle du Soleil. Ainsi, vu depuis une autre étoile, le transit de la Terre devant le Soleil ne dure que 13 h une fois tous les ans, et celui de Jupiter ne dure que 30 h une fois tous les douze ans, ce qui illustre à nouveau la rareté du phénomène. Bien évidemment, la mesure de la période requiert l’observation d’au moins deux transits.