L’observation photométrique du transit ne fournit que le rapport du rayon de la planète à celui de l’étoile, pas le rayon absolu de la planète. Par ailleurs, sauf dans les cas où des perturbations gravitationnelles entrent en jeu (TTV), les transits en eux-mêmes ne contraignent pas les masses planétaires.
Densité des exoplanètes
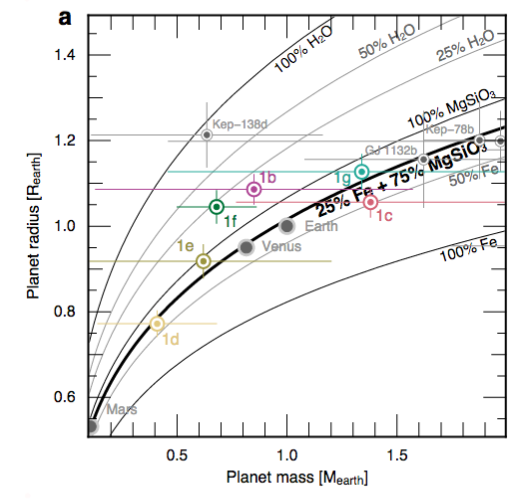
Diagramme masse-rayon des planètes TRAPPIST-1, comparées aux planètes telluriques du Système Solaire et quelques autres exoplanètes. Sont montrées aussi les courbes theoriques pour des planètes de différentes compositions
Crédit :
Gillon et al. 2017
A nouveau, une limitation est que 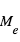 n’est pas connue. Il faut donc combiner les mesures de transit et de vitesse radiale avec des informations indépendantes sur l’étoile, typiquement obtenues via les modèles d’évolution stellaire, qui donnent des relations entre âge, luminosité, rayon, masse et composition.
n’est pas connue. Il faut donc combiner les mesures de transit et de vitesse radiale avec des informations indépendantes sur l’étoile, typiquement obtenues via les modèles d’évolution stellaire, qui donnent des relations entre âge, luminosité, rayon, masse et composition.
Par ailleurs, comme indiqué en 2.2, la profondeur du transit 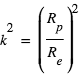 , la durée du transit T et la durée de l’ingress/egress contraignent le rapport
, la durée du transit T et la durée de l’ingress/egress contraignent le rapport 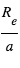 et le paramètre d’impact b, ce qui permet de « calibrer » le rayon planétaire en absolu. Si les propriétés stellaires sont suffisamment bien connues, on peut donc obtenir des valeurs absolues du rayon et de la masse planétaire, donc de sa densité, ce qui a évidemment une importance énorme pour contraindre la nature (gazeuse, glacée, rocheuse) et la structure interne de la planète.
et le paramètre d’impact b, ce qui permet de « calibrer » le rayon planétaire en absolu. Si les propriétés stellaires sont suffisamment bien connues, on peut donc obtenir des valeurs absolues du rayon et de la masse planétaire, donc de sa densité, ce qui a évidemment une importance énorme pour contraindre la nature (gazeuse, glacée, rocheuse) et la structure interne de la planète.
Finalement, en combinant la relation ci-dessous avec la 3e loi de Kepler, on peut déterminer la gravité planétaire 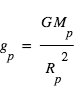 indépendamment des propriétés de l’étoile :
indépendamment des propriétés de l’étoile :
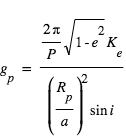 La connaissance de
La connaissance de 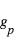 est nécessaire pour l’élaboration de modèles d’atmosphères.
est nécessaire pour l’élaboration de modèles d’atmosphères.
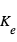 sur l’étoile est relié à la masse planétaire par :
sur l’étoile est relié à la masse planétaire par :
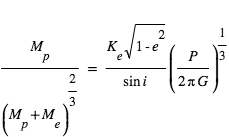 où
où 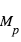 et
et 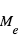 sont la masse planétaire et stellaire, e l’excentricité, P la période, et G la constante universelle de gravitation. L’avantage ici est qu’on peut écrire
sont la masse planétaire et stellaire, e l’excentricité, P la période, et G la constante universelle de gravitation. L’avantage ici est qu’on peut écrire 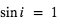 .
.

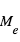 n’est pas connue. Il faut donc combiner les mesures de transit et de vitesse radiale avec des informations indépendantes sur l’étoile, typiquement obtenues via les modèles d’évolution stellaire, qui donnent des relations entre âge, luminosité, rayon, masse et composition.
n’est pas connue. Il faut donc combiner les mesures de transit et de vitesse radiale avec des informations indépendantes sur l’étoile, typiquement obtenues via les modèles d’évolution stellaire, qui donnent des relations entre âge, luminosité, rayon, masse et composition.
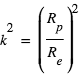 , la durée du transit T et la durée de l’ingress/egress contraignent le rapport
, la durée du transit T et la durée de l’ingress/egress contraignent le rapport 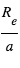 et le paramètre d’impact b, ce qui permet de « calibrer » le rayon planétaire en absolu. Si les propriétés stellaires sont suffisamment bien connues, on peut donc obtenir des valeurs absolues du rayon et de la masse planétaire, donc de sa densité, ce qui a évidemment une importance énorme pour contraindre la nature (gazeuse, glacée, rocheuse) et la structure interne de la planète.
et le paramètre d’impact b, ce qui permet de « calibrer » le rayon planétaire en absolu. Si les propriétés stellaires sont suffisamment bien connues, on peut donc obtenir des valeurs absolues du rayon et de la masse planétaire, donc de sa densité, ce qui a évidemment une importance énorme pour contraindre la nature (gazeuse, glacée, rocheuse) et la structure interne de la planète.
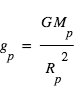 indépendamment des propriétés de l’étoile :
indépendamment des propriétés de l’étoile :
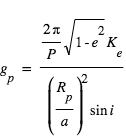 La connaissance de
La connaissance de 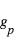 est nécessaire pour l’élaboration de modèles d’atmosphères.
est nécessaire pour l’élaboration de modèles d’atmosphères.